试谈数形结合在数学教学中几个“点”

张练

摘  要：小学数学是小学众多学科中非常重要的基础应用学科，小学数学教学最根本就是要帮助学生认识数字和识别形状。在小学数学教学实践中，应用数形结合思想，将这两个方面有机地融合在一起，可以产生很好的教学效果。本文总结了在小学数学教学中把抽象的概念直观化、把算理算法规律形象化、把复杂的问题简单化这几条具体的应用策略，以帮助数学教师在教学实践中有效的应用这一教学思想。

关键词：数形结合;小学数学;应用

数形结合教学是小学数学教学中一个重要的教学方法之一，它能够让复杂变为简单，让抽象变为形象，让繁琐变为明朗，有助于帮助学生对数学概念的掌握和记忆，对解题思路的理清，对算理算法的理解，从而提高教数学教学质量。但如何利用好数形结合思想，结合自己多年的教学，就此谈点看法。

一、找准数形结合的“切入点”  让概念问题变得“简单化”

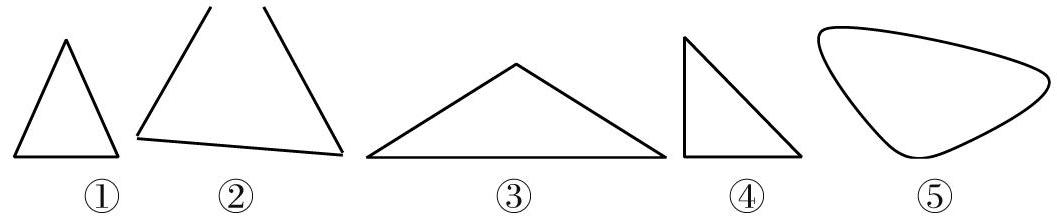
数学概念很抽象，而小学生毕竟由于年龄小，特别是低年级学生，抽象思维还在雏形阶段，体现的大都是具体的形象思维，但在中高年级，随着知识面的不断扩大，数学概念的不断增多，会不断向抽象逻辑思维过渡，会出现一定的难度。也需要通过凭借事物的具体形象或表象来呈现。因此，我们在数学概念问题教学中，引入数形结合思想，找准数形结合的“切入点”，使学生对数学概念有着更加透彻的理解。比如，在学习什么是“三角形”的概念，书上表述为“由三条线段围成的图形，叫做三角形”，在教学时，如果教师单从只字面上去讲解，学生不但难以理解，也无法形成正确的概念。所以就应该抓住“三条线段”和“围成”字的切入点，在黑板上画出三角形，让学生指出哪是“三条线段”，怎么才能算“围”，从图形中把“三角形”的概念 “直观化”，从“看”中在自己的头脑中去形成“三角形”的概念，明确组成三角形的条件是三条边的封闭图形，理解“三角形”概念的真正涵义。然后，在黑板上在画出一下是三角形或类似三角形图形：

师：上面的图形都是三角形吗？

生：有些是，有些不是。

师：哪些是三角形？哪些不属于三角形？

生：①③④是三角形，②⑤不是三角形

师：为什么？能说说理由吗？

生：②没有围城，⑤三条边不是线段。

师：对，看来同学生对三角形的概念已经理解。

在这里，学生对三角形的涵义已经掌握，理解了三角形的本质属性，通过这样数形结合的教学方式，学生对数学知识会有更加深入的理解，课堂教学的效果会非常理想。

二、把握数形结合的“契合点”让算理问题变得“清晰化”

在数学计算环节教学中，算法算理是教学中的一个难点，如何让学生更容易对算理的接受、理解和运用，这是我们在教学中要深入思考和积极探索的问题。在教学中，渗透数形结合思想，运用数形结合的方法，把握准数形结合的“契合点”，能够很好地让学生理解和掌握算理。

如在教学“两位数乘两位数的笔算”整堂课的教学过程中，无论是理解题意、口算和笔算，还是理解算法和算理，都利用点子图来进行辅助教学，将抽象的数字形象化，将具体的计算步骤直观化，将繁杂的计算方法具体化，将难懂的算理清晰化，更便于学生对新知识的理解和掌握。因此在计算教学时用“数形结合”的方法，有利于中低年级段的学生掌握算法理解算理。

比如：计算14×12

师：在计算14×12的过程中，我们得到这样的四个数： 8、20、40、100

师：你们能在点子图中找到它们吗？

学生在点子图中找出四个数所在位置，教师课件展示。（如下图）

师：（在图中将8个点和20个点圈起来）圈起来的部分对应竖式中的哪部分？

生：28

师：这个28是哪两个数的乘积？

生：14×2的积

师：28是几套书的本数？

生：2套书的本数。

师：（在图中将40个点和100个点圈起来）这又对应着竖式中的哪个部分？

生：140

师：它是哪两个数的乘积？

生：14×10的积

师：是几套书的本数呢？

生：10套书的本数。

师：最后我们把28和140相加，得到168。168是哪两个数的乘积？

生：14×12的积。

师：也就是几套书的本数？

生：12套书的本数。

在这里，借助点子图这个“契合点”，进行“数”与“形”的结合来讲清楚算理，这种直观表象形式，表示竖式中相对应的数字，同时把竖式中的数字在点子图中找出对应的部分，整个教学环节形象直观，激发学生的学习兴趣，提高了学生的抽象思维能力。数形结合的方法，有利于学生直观地理解算法和算理。

三、寻求数形结合的“突破点”让应用问题变得“直观化”

应用数学解决实际问题既是数学的特点， 也是学习数学的目的之一。解决实际应用问题，比如“行程问题”“植树问题”“工程问题”等等，在平常的教学中，一般都是让学生审题，找出已知条件，理清数量关系， 然后进行解答，这对题目比较简单的学生都容易进行直接解答，但对比较难的应用问题，学生往往无从入手，所以，这就需要充分利用数形结合思想，寻求它的“突破点”，通过数与形之间的相互转化，通过数形结合化“抽象”为“直观”，通过线段图，从线段图中进行比较，直观地发现数量之间存在的联系，从而分析解决问题的思路方法。

例如，小明的爷爷在果园种植果树，种了桃树50课，种的桃树比种的李树多1/4，爷爷一共种了多少棵果树？

这道题对判断谁是单位“1”有一定的困难，谁比谁多了几棵没有明确数据，该用乘还是除，很多学生难以理解题目的真正意思，易混淆分数乘除法，学生难以进行解答。这时，如果老师不失时机渗透数形结合的思想方法，找出“突破点”，引导学生依据题意画出相应的线段图，让学生一目了然的知道种的桃树比种的李树多，并多了1/4，才能帮助学生迅速找出等量關系列出方程，通过线段图写出等量关系式：种植李树的棵树+比种植李树多1/4 桃树的棵树=种植桃树的棵树，求出种植李树的棵树，然后在求出一共的棵树就容易解决了。单位“1”是种植李树的棵树，可以用方程解：设种植李树的棵树为“X”，列式.X+1/4X=50，解得X=40，即种植李树的棵树为40棵，爷爷在果园里一共种植了90棵果树。

这里，通过数形结合，从“突破点”入手，准确的找到数量之间的联系，进行比较、分析，得出算式，解答出要求的问题，这里实际上就是把复杂、抽象的问题形象化，变得“简单”明了，降低题目的难度，加深了学生的理解，这样不仅提高了学生的发散思维能力，还培养学生的数形转换能力和多角度思考问题的能力。

总之，在数学教学中，帮助学生解答相关的问题，需要充分发掘“数”与“形”的本职联系，利用数形结合思维，去努力探索分析问题和解答问题，掌握算法算理、解题技巧，培养学生的数学思维，提高学生学习数学的兴趣与积极性。

参考文献

[1]刘敬娟.“数形结合”思想在小学数学教学中的渗透[J].新课程（小学）.2015年12期.

[2]陈水秀.对小学数学教学中数形结合思维运用探究[J].课程教育研究.2019年11期.

[3]廉萌.“数形结合”思想在小学数学教学中的应用[J].青少年日记（教育教学研究）.2019年04期.

[4]赵静.小学数学教学中数形结合思维运用探究[J].科学咨询（教育科研）.2018年08期.

[5]对小学数学教学中数形结合思想的分析[J].数学大世界（上旬）.2019年02期.

[6]数形结合，理解算理——数形结合在小学高段数学教学中的运用[J].新课程（小学）.2019年06期.

[7]“数形结合”在小学数学教学中的运用策略探讨[J].新课程（小学）.2018年12期.

[8]“数形结合”思想在小学数学教学中的应用分析[J].中国校外教育.2018年33期.

龙岩师范附属小学