基于聚类分析的存款保险费率影响因素研究

吴苏林 吴一凡 杨胜刚

摘 要：以某省82家农村商业银行为对象，用单一财务指标及其组合指标衡量银行的风险水平，采用K-means聚类方法得到农村商业银行的风险级别和费率等级，根据样本风险级别与费率等级确定影响存款保险费率的重要因素。研究表明：资本充足率是影响存款保险费率的最重要的单一指标，影响程度为59.76%;由资本充足率、不良贷款率、拨备覆盖率及成本收入构成的组合指标影响费率的程度最高为90.24%，组合的预测准确率不低于80%。

关键词： 存款保险费率;农村商业银行;影响因素;K-means聚类方法

中图分类号：F832.1   文献标识码： A    文章编号：1003-7217（2021）03-0035-07

一、引言及相关文献综述

1933年美国建立存款保险制度以来，该制度在全球范围内得到广泛推广。研究表明，存款保险制度有利于防范银行挤兑风险、保护存款者利益以及稳定金融体系[1-4]，在国家金融安全网中正发挥越来越重要的作用。据国际存款保险协会（IADI）数据显示，截至2020年4月，共有146个国家（地区）建立存款保险制度。我国于2015年正式实施《存款保险条例》，要求所有存款类金融机构按规定向管理机构缴纳保费。存款保险制度的核心是费率厘定，我国实施的差别化费率是根据银行的经营状况和风险水平制定不同的标准，能有效避免单一费率所带来的道德风险和逆向选择等问题。因此，从银行风险视角分析费率的影响因素，有利于在当前银行业竞争压力加剧的背景下合理制定费率标准，保障存款保险制度的有效运行。

目前，有关存款保险定价的研究以期权定价法及预期损失定价法为主。以Merton（1977）为代表的期权定价法认为，投保机构缴纳的保费与其资产价值、资产价值的波动率、无风险利率以及投保的期限有关[5-7]。此后，学者在Merton的基础上重新度量了银行资产价值及波动率 [8-10]。国内外学者将债务清偿结构、监管宽容及所得税效应纳入拓展模型中[11-13]，也有学者研究了利率风险、信贷风险及系统性风险等对存款保险定价的影响[14-16]。预期损失定价方法的思想是根据银行破产给储户带来的预期损失确定保费，由投保机构的预期违约概率、风险敞口及违约损失率之积得出[17-19]。该方法克服了期权定价方法仅适用于上市银行的缺陷，为非上市银行的保费定价提供了新的思路[20]。

定价方面的研究为完善存款保险制度提供了丰富的理论基础，但在实践层面上，较少国家采用期权定价法和预期损失定价法来确定银行的真实保费。以美国为例，1993年率先采用风险差别费率制度，根据CAMELS评级和资本等级划分银行风险等级，以此作为收取不同费率的依据。2016年7月1日，美国进一步完善风险差别费率制度，颁布了《小型银行存款保险费率制度》，以更能及时反映银行风险状况的财务指标法确定费率水平。具体来说，新财务指标法是用加权平均的CAMELS与7个财务指标分别乘以定价乘数，加总得到初始费率。由此可见，美国联邦存款保险公司将影响费率水平的因素聚焦于银行自身的经营管理和风险水平，这对研究我国中小银行差别费率的影响因素具有指导和借鉴意义。

目前的研究亟需从以下三方面完善：首先，有关存款保险费率影响因素的实证研究较少，最主要的原因是真实的费率数据难以获取。已有研究大多以定价模型为基础，加入可能的影响因素并重新测算费率大小后得出结论，但这往往会受到模型设定和假设条件的干扰。其次，银行自身的风险水平是决定费率大小最直接关键的因素，CAMELS评级是确定银行风险等级的重要方法之一，评级体系分别对资本充足率、资产质量、经营管理、盈利水平、流动性和市场风险敏感度赋予了不同的权重，代表了各自在风险评级中的重要程度，间接地反映对费率大小的影响程度，但少有实证研究从银行的财务实力和經营管理状况来分析真实费率的影响因素。最后，现有研究对中小银行的费率影响因素关注较少。近年来我国改革进程不断推进，银行间竞争压力有增无减，中小银行因抗风险能力较弱，难以抵御较大的金融风险，破产概率高于大型银行[21]。因此，明确中小银行的费率影响因素有利于监管机构完善中小银行费率核定体系，促进中小银行稳健运营。

为此，本文收集了某省82家农村商业银行存款保险相关数据，并参考美国的小银行费率制度以财务指标法衡量农村商业银行的风险水平，实证分析影响银行真实费率的因素及其重要程度。在方法上，选用机器学习中的聚类分析，将真实费率和财务指标聚类分组，根据费率等级和风险等级匹配程度确定影响因素。相对回归模型较多的前提假设，聚类分析更加简便高效。

二、研究方法

经济学领域中多元线性回归模型常被用来研究变量间的影响关系。随着自变量的增加，分析单变量对因变量的相对重要性会变得复杂。另外，变量间的线性关系是模型使用的前提，但衡量银行风险的财务指标是否与真实费率呈现线性关系，是否会在其他指标的共同作用下改变影响程度，考虑这些问题也会增加模型的复杂度。随着大数据时代的到来，机器学习技术迅速发展并广泛应用于多个领域[22]。其中，无监督学习无论从学习能力还是从人工成本上看，挖掘分析数据的潜力更大。聚类分析是无监督学习中最常用的一种方法，其目的是将具有相似特征的数据分在同一组，组内相似度越高，组间差别度越大，聚类的效果越好[23]。利用计算机处理数据的能力，该方法能高效精准地从复杂数据中提取有用信息。本文根据不同的财务指标聚类样本，进而匹配不同级别的费率，不仅能根据匹配率分析影响因素的重要程度，也能避免指标间相互干扰所产生的问题。

相对而言，聚类分析的算法中基于划分的算法相对运用得较为广泛。该算法是先指定好聚类中心或聚类个数对数据初步分组，通过迭代反复调整样本与各组之前的距离，直到最优函数收敛。K-means聚类算法作为基于划分算法中经典算法之一，于1967年由MacQueen正式提出，因其简单高效的特征一直被学术界广泛应用于不同学科领域[24-27]。该算法需要预先指定K个组，随机选取K个中心，计算各数据与随机中心间的距离，将数据分配到距离最近的一组，通过迭代更新中心点从而使各组总的误差平方和SSE最小。

通过聚类分析确定费率影响因素的过程：首先，根据农村商业银行缴纳的真实保费将82家农村商业银行聚类分为3个等级;其次，从CAMELS评级的6个方面选择财务指标，标准化财务指标后再次聚类划分样本;最后，计算两次样本划分的匹配率确定费率影响因素及影响程度。各个财务指标度量了银行不同方面的风险水平，在实际中银行面临的风险更加复杂多样，需要考虑多个财务指标综合确定银行风险水平。因此，分别从单个财务指标、两两组合的财务指标以及3个财务指标组合聚类划分样本风险等级，多方面地确定费率的重要影响因素。但多指标间可能存在相互增强或抵消的作用，简单组合后可能无法真实反应银行的风险水平。管理者在银行风险评估时往往采取谨慎保守态度，即考虑极端情况或是最坏情形，帮助管理者了解银行面临的潜在风险及抵御风险的能力，这在理论研究和实践中发挥着重要作用[28-31]，因此，引入该思想修正银行的风险等级。具体方法为：若多指标组合后得到的风险等级与费率等级不符，则取组合中级别最高（风险最大）的单个指标所对应的风险等级作为银行最终风险评级，再次比对风险等级和费率等级是否一致，得到匹配率。

三、数据选取及描述

我国银行每年缴纳两次保费，选取2017年下半年某省82家农村商业银行作为研究对象，根据其缴纳的保费计算出适用的存款保险费率。该省82家农村商业银行所用的财务指标来源于年报数据、监管报表及相关计算。

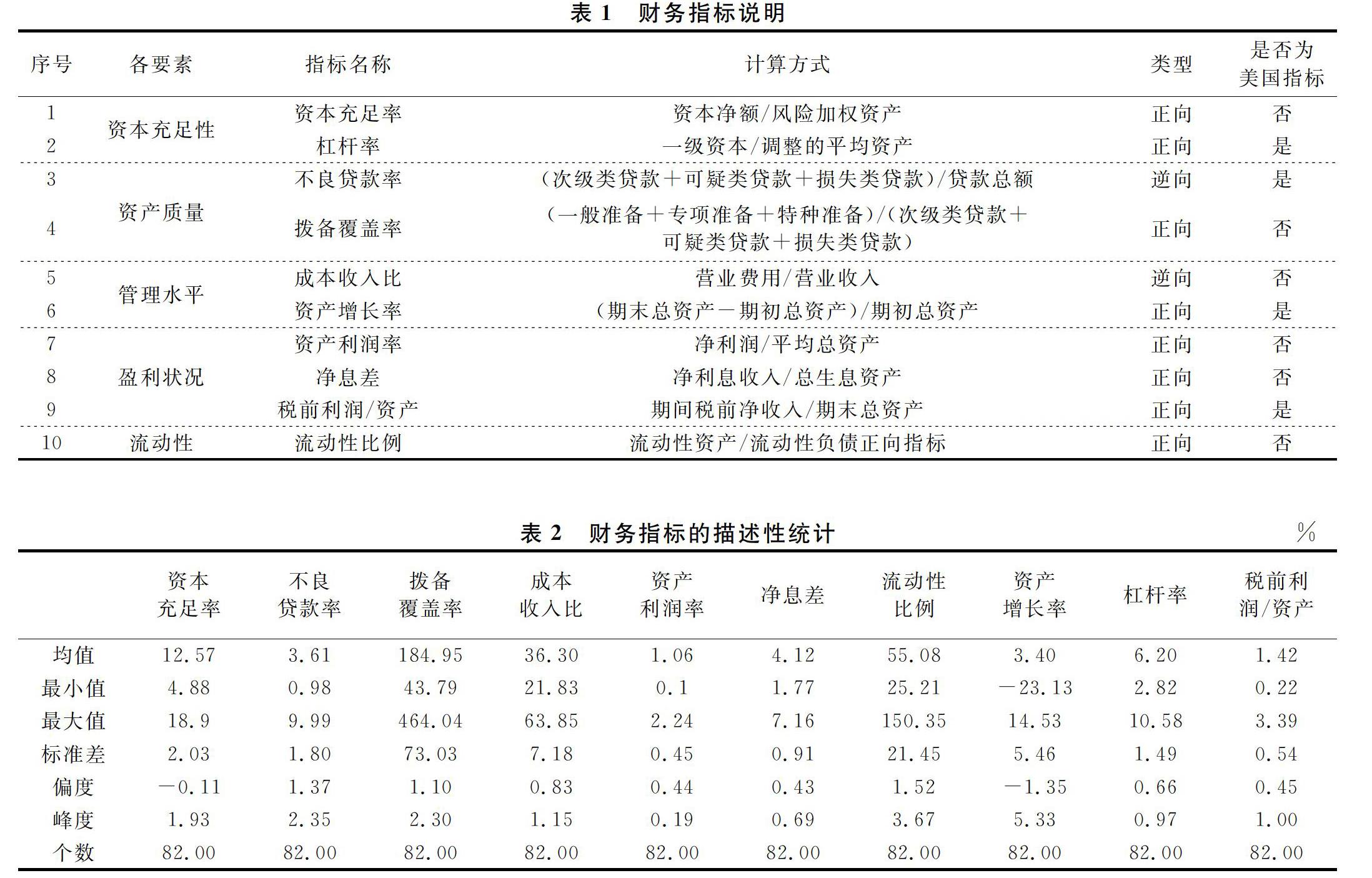
财务指标的选择对应CAMELS评级的6大方面，分别是资本充足性、资产质量、经营管理、盈利水平、流动性和市场风险敏感度。考虑样本多为未上市的金融机构及数据的可获得性，从前5大方面选取了7个财务指标，借鉴美国中小银行费率制度添加3个财务指标，共选取了10个财务指标。

在资本充足性方面，我国监管部门采用资本充足率、一级资本充足率及核心一级资本充足率作为衡量标准。资本充足率由银行的资本净额与风险加权资产的比值计算而来，反映了银行在债权人和存款人利益受损时，可用自有资本承担损失的能力。由于样本的资本充足率与一级资本充足率相差不到1%，一级资本充足率和核心一级资本充足率完全一致，因此，选取资本充足率作为资本充足性方面的评价指标。此外，美国费率体系下的杠杆率反映银行一级资本占资产的比重，将其作为评价资本充足性的另一重要指标。

在资产质量方面，银行主要的资产风险来源于贷款质量。美国以不良贷款及租赁/总资产来衡量资产质量。鉴于某省农村商业银行实际经营及数据可获得性，用不良贷款率替代，即银行的次级、可疑及损失贷款之和与贷款总额之比。不良贷款率越高意味着银行的信贷资产质量越差，不能收回贷款的可能性越大。此外，拨备覆盖率衡量了银行对不良贷款实际计提的损失准备，也是考察银行资产质量的重要指标。

经营管理方面的考核主要包括银行业务政策、管理者的经历经验及职员培训等非定量因素，因无定量指标多选用其他指标代替。本文选取了成本收入比作为第一个评价指标，反映了银行每单位收入所需付出的成本，该比率越低意味着银行的经营管理能力越好。借鉴美国新费率制度，选择资产增长率作为第二个指标，通过银行资产规模的增长水平判断银行的发展潜力。

在考察盈利状况方面，资产利润率是常用指标之一。存贷款业务作为银行的核心，净利息收入在全部生息资产的比值也是重要的评价指标。此外，加入美国制度的税前利润/资产指标，更全面地体现银行运用资产获利的能力。

流动性对银行的经营管理活动至关重要，若银行因流动性不足造成挤兑现象，很可能引发系统性风险，严重影响金融体系的稳定性。流动性方面主要考量资产负债的管理能力、资金变现及筹集资金等能力，选取流动性比例作为衡量指标。

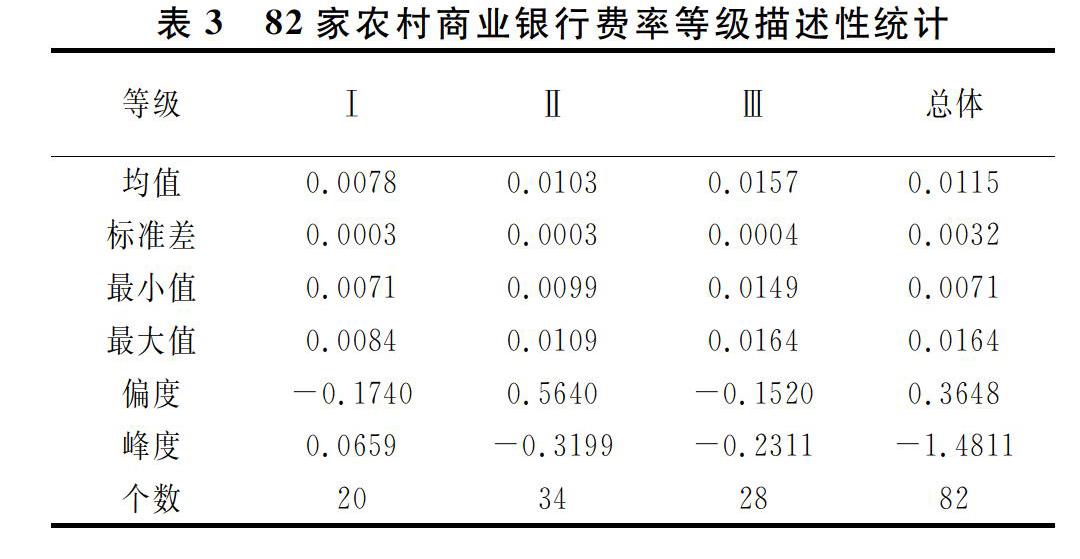
10个指标因衡量的方面和角度不同分为正向和逆向指标，分析前需要将各指标一致化。正向指标的标准化方法为（x-min ）/（max -min ），逆向指标的标准化方法是（max -x）/（max -min ）。汇总指标的计算方式及类型如表1所示。10个财务指标的描述性统计如表2所示。

平均来看，资本充足率为12.57%，高于监管机构对非系统重要性银行规定的10.5%;不良贷款率为3.61%，低于国际标准的不良资产率警戒线10%;拨备覆盖率为184.95%，高于120%～150%的监管标准;成本收入比为36.30%，略微高于35%;资产利润率为1.06%，不低于风险监管核心指标规定的0.6%;杠杆率符合我国不低于4%的监管要求;流动性比例同样满足我国监管机构对商业银行的流动性规定。此外，样本的拨备覆盖率、流动性比例和存贷款比率的标准差较大，即各家农村商业银行在计提损失和流动性方面有明显差异，而在其他指标如资产利润率和净息差表现出较小差异。

四、结果分析

存款保险费率是应缴保费与被保存款余额的比值。根据2017年下半年保费及相关数据，计算出每家农村商业银行的存款保险费率。利用K-Means聚类方法，设置最大迭代次数为50次，K值设置为3，得到82家农村商业银行的费率等级，如表3所示。聚类结果显示，组间平方和与总平方和的比值为99.1%，依据费率大小分为3个等级较为合理。

根据表3，82家农村商业银行的费率可分为3个等级，级别越高，对应的费率值越大，意味着银行的风险状况及经营管理水平越差。从分类结果看，等级Ⅰ的费率均值为0.0078，适用费率Ⅰ的银行占比24.39%;等级Ⅱ的费率均值为0.0103，适用该档费率的银行占全样本的41.46%;等级Ⅲ的费率均值为0.0157，适用该档费率的银行占比为34.15%。

将10个指标分别标准化，值越高代表银行在对应的评价方面表现越好，风险等级越低。再次使用K-means聚类方法将样本分为3类，计算费率等级与风险等级相匹配的样本数量占比。10个指标的匹配率如表4所示。

根据匹配率可知，资本充足率、资产利润率、税前利润/资产及拨备覆盖率4个指标单独解释费率等级的正确率至少为50%。但仅使用单个财务指标作为确定金融机构使用的费率等级缺乏合理性，且单个指标的正确率并未超过75%。因此，进一步在10个指标中选取2个随机组合，共得到45种组合，根据组合指标值再次分类样本。具体的方法是随机组合2个财务指标，標准化后赋予相同权重，得到组合财务指标值。2个财务指标组合解释费率等级的程度如表5所示。

根据表4推测，4个匹配率最高的指标两两组合后也应是影响费率水平最大的前6个指标组合。表5结果显示，财务指标两两组合后，有4个组合符合预期。资本充足率和资产利润率、资本充足率和税前利润/资产对费率的影响程度最大，匹配率均为63.41%;资本充足率和拨备覆盖率对费率的影响为60.98%;资产利润率和税前利润/资产对费率的综合影响为57.32%。此外，不良贷款率和成本收入比、成本收入比与税前利润/资产的组合匹配率均为58.54%。结合表4、表5分析，匹配率最高的组合指标对费率的影响程度比单一指标高不到5%，且存在指标组合后影响程度变化的现象。在指标两两组合中，赋予指标相同的权重。但在实际中，监管者往往采取更为谨慎的风险评估态度，可能赋予更大的权重给更能反映银行风险的指标或根据银行面临的最大风险评定风险等级。考虑“最坏情况”的思想在风险管理中非常重要，本文引入这一思想提高研究的可信度。

具体而言，选出财务等级与费率等级不符的个体，将组合指标中等级最高的单一指标评级作为最终的财务等级，再次比对与费率等级的相符程度，得到修正后的匹配率，结果如表6所示。

表6和表5对比发现，基于风险管理思想修正后，组合财务指标能更好地解释费率等级。首先，表5中匹配率从高至低排序位列前6的组合（资本充足率和资产利润率、资本充足率和税前利润/资产、资本充足率和拨备覆盖率、不良贷款率和成本收入比、成本收入比和税前利润/资产、资产利润率和税前利润/资产）对应在表6中分别提升了9.76%、9.76%、4.87%、4.87%、15.85%、1.22%。其次，修正后对费率影响最大的前三组财务指标与修正前相比也发生了变化，如表6所示，不良贷款率和拨备覆盖率组合对费率等级修正后的影响高至86.59%，资本充足率和不良贷款率组合后对费率的影响显著提升至80.49%，资本充足率和成本收入比的综合影响程度也位居前三，匹配率为75.61%。最后，除资本充足率和拨备覆盖率外，不良贷款率和成本收入比也是监管机构评估的重点。

本文进一步研究多因素对费率的综合影响，用同样的方式将3个财务指标随机组合，共得到120个组合指标，并基于风险管理的思想修正结果。匹配率为前三的组合如表7所示。

表7显示取3个指标算术平均值作为组合指标值进行聚类，财务等级与费率等级的匹配度并不高，而修正后的解释力度大幅提升。资本充足率、不良贷款率和拨备覆盖率三个指标组合后的影响力高达90.24%，资本充足率、不良贷款率和成本收入比的组合为86.59%，不良贷款率、拨备覆盖率和成本收入比的组合为85.37%。显然，三个指标相互组合对费率等级的影响高于两两组合的影响。

为验证结论的普遍适用性，从样本中随机挑选41家，选择2018年上半年的费率及财务指标数据，重复上文的研究方法，得到财务指标等级与费率等级如表8所示。

10家农村商业银行的费率等级为Ⅰ，19家的费率等级为Ⅱ，剩余12家的费率为Ⅲ等级，各等级的银行数量占比分别为24.39%，46.34%和29.27%。

在资本充足率、不良贷款率、拨备覆盖率及成本收入比中随机选取3个指标得到4个组合。修正后的匹配度依然非常高，表明资本充足性、资产质量及管理水平是影响费率水平的重要因素，最高可在97.56%的水平上解释费率等级，结果如表9所示。

随机抽取41家银行并运用相同的聚类算法和修正方法，结果显示在2018年上半年，这4个指标解释程度仍在80%以上，说明本文的研究结果具有稳健性。

五、结论及启示

通过K-means聚类方法研究了存款保险费率的影响因素。结论1：资本充足率是影响存款保险费率最重要的单一因素，影响程度高达59.76%。这一结论从理论上验证了《中华人民共和国商业银行法（修改建议稿）》中有关金融机构风险监管及处置机制的规定，其中明确规定监管机构或存款保险基金管理机构根据商业银行的资本充足率水平采取相应的早期纠正，因此监管机构在实际操作中需重点关注投保机构资本充足率的变化，同时也应拓宽中小银行的资本补充渠道，完善资本补充机制，提高中小银行的抗风险能力。结论2：多个财务指标组合后能更全面地反应银行的风险水平，与费率等级的匹配度更高。资本充足率和资产利润率作为前两大重要因素，组合后对费率的影响程度提高至63.41%，依然是最重要的组合指标。此外，资本充足率、不良贷款率、拨备覆盖率及成本收入比的3个进行组合后解释费率等级的正确率最高为90.24%。因此监管机构制定中小银行费率时应重点关注其资本充足性、资产质量及管理水平，及时根据风险水平调整费率等级，促进银行公平竞争和审慎经营。结论3：美国小型银行存款保险费率制度对我国农村商业银行具有一定适用性。本文借鉴美国直接采用财务指标法确定小型银行费率的方法，得到解释真实费率水平80%以上的影响因素，说明选用的财务指标较好地反映银行风险信息，有利于小银行审慎经营，对完善我国小型银行存款保险制度的早期纠正功能具有一定借鑒意义。

参考文献：

[1] 张亚涛.存款保险定价模型之探究[J].国际金融研究，2003（11）：35-38.

[2] 谢平，王素珍，闫伟.存款保险的理论研究与国际比较[J].金融研究，2001（3）：1-12.

[3] 田国强，赵禹朴，宫汝凯.利率市场化、存款保险制度与银行挤兑[J].经济研究，2016（3）：96-109.

[4] 王道平.利率市场化、存款保险制度与系统性银行危机防范[J].金融研究，2016（1）：50-65.

[5] Merton R C . An analytic derivation of the cost of deposit insurance and loan guarantees： An application of modern option pricing theory[J]. Journal of Banking and Finance， 1977（1）： 3-11.

[6] Black F ， Scholes M . The pricing of options and corporate liabilities[J]. Journal of Political Economy， 1973（81）： 637-659.

[7] Merton R C . The theory of rational option pricing[J]. Bell Journal of Economics and Management Science， 1973（4）： 141-183.

[8] Marcus A J ， Shaked I . The valuation of FDIC deposit insurance using option-pricing estimates[J]. Journal of Money， Credit and Banking， 1984， 16（4）： 446-460.

[9] Merton R C . On the cost of deposit insurance when there are surveillance costs[J]. Journal of Business， 1978， 51（7）： 439-451.

[10]Ronn E I ， Verma A K . Pricing risk-adjusted deposit insurance： An option-based model[J]. Journal of Finance， 1986， 41（9）： 871-895.

[11]张金宝，任若恩.基于银行债务的清偿结构存款保险定价[J].金融研究，2007（6）：35-43.

[12]明雷，杨胜刚，邓世杰.监管惩罚、监管宽容和存款保险价格[J].管理科学学报， 2019， 22（8）：59-70.

[13]姜兴坤，孙健，宋玉.引入所得税的Merton模型存款保险定价研究[J].统计与信息论坛，2013，28（3）：22-27.

[14]Duan J C ， Moreau A ， Sealey C W . Deposit insurance and bank interest rate risk： Pricing and regulatory implications[J]. Journal of Banking and Finance， 1995， 19： 1091-1108.

[15]Dermine J ， Lajeri F . Credit risk and the deposit insurance premium： A note[J]. Journal of Economics and Business， 2001， 53（5）： 497-508.

[16]Lee S C ， Lin C T ， Tsai M S . The pricing of deposit insurance in the presence of systematic risk[J]. Journal of Banking and Finance， 2015（51）： 1-11.

[17]魏志宏.中国存款保险定价研究[J].金融研究，2004（5）：99-105.

[18]刘海龙，杨继光.基于银行监管资本的存款保险定价研究[J].管理科学学报，2011，14（3）：73-82.

[19]繆锦春，季安琪.基于预期损失理论的中国存款保险定价[J].湖南科技大学学报（社会科学版），2015（3）：99-104.

[20]魏修建.我国地方性商业银行存款保险定价研究——基于预期损失定价模型的分析[J].经济问题，2014（11）：44-48.

[21]明雷，秦晓雨，朱红.存款保险研究新进展：定价和制度效应[J].财经理论与实践，2019，40（6）：39-46.

[22]何清，李宁，罗文娟，等.大数据下的机器学习算法综述[J].模式识别与人工智能，2014（4）：327-336.

[23]张静.数据挖掘中聚类分析综述[J].价值工程，2014（15）：226-227.

[24]MacQueen J. Some methods for classification and analysis of multivariate observation[C]∥Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley：University of California Press，1967：281-297.

[25]石云平，辛大欣.基于K-means聚類算法的分析及应用[J].西安工业学院学报，2006（1）：45-48.

[26]周爱武，于亚飞. K-means聚类算法的研究[J].计算机技术与发展，2011（2）：62-65.

[27]杨俊闯，赵超.K-Means聚类算法研究综述[J].计算机工程与应用，2019，55（23）：7-14.

[28]潘岳汉，易晓溦.商业银行压力测试宏观情景构建及应用——基于FAVAR模型[J].金融论坛，2018（11）：3-14.

[29]彭建刚，易昊，潘凌遥.基于行业相关性的银行业信用风险宏观压力测试研究[J].中国管理科学，2015（4）：11-19.

[30]宋良荣，王文硕，陈锦磊.基于流动性覆盖率的商业银行压力测试实证研究[J].金融监管研究，2016（5）：31-47.

[31]方意.中國银行业系统性风险研究——宏观审慎视角下的三个压力测试[J].经济理论与经济管理，2017（2）：48-66.

（责任编辑：厉 亚）

Abstract：This paper studies 82 rural commercial banks in a province and uses K-means clustering method with the group standard of the deposit insurance premium rate and single financial index or combined index to get banks' ratings of insurance premium and risk profiles， and then matches the two ratings to find important factors affecting the deposit insurance premium rate. The results show that the capital adequacy is the most important single factor that affects the deposit insurance premium rate， and the influence degree is 59.76%; the combination of capital adequacy， non-performing loan ratio， provision coverage ratio and cost/income ratio can affect the premium rate， the combined index has a maximum influence on the premium rate of 90.24%， and the forecast accuracy of the combination is no less than 80%.

Key words：deposit insurance premium rate; rural commercial bank; factors; K-means clustering method