掺杂软质空心小球对质子交换膜内裂纹捕捉能力的研究*

杜 新，朱亚南

(长春理工大学机电工程学院，吉林 长春 130022)

引言

质子交换膜燃料电池被认为是下一代动力源的理想方案，提高耐久性是其商业化成功的关键之一.由于质子交换膜被机械地约束在燃料电池中，电池工作状态变化导致电池内水分改变[1]，因此，在湿热变化过程中其动态吸水特性会产生周期性的机械应力，并在应力集中的位置引发裂纹及扩展[2].裂纹扩展会导致氢气渗透加剧、局部高温等许多负面影响.阻止和减缓膜内裂纹扩展，提高燃料电池耐久性成为各国学者研究热点.

目前对膜内裂纹的研究主要从两个方面展开，一是改善电池运行工况，通过减少工作温度、相对湿度、氢气压力和电池电势等，降低裂纹对氢气渗透的影响.二是改变电池内的结构和材料，如自增湿膜在质子交换膜内掺杂催化剂Pt颗粒，提高膜内水含量[3].Wang等研究在膜内掺杂微胶囊，当其和膜内缺陷(例如裂缝和针孔)相遇时，胶囊破裂并释放预填充的Nafion溶液，就地修复缺陷[4].通过掺杂改变材料机械性能是复合材料研究中常用的方法，硬质掺杂可使裂纹远离掺杂物，而软质掺杂会吸引裂纹.吕斐等研究发现孔洞产生的应力集中对裂纹扩展也会产生“吸引”作用[5].同时，Stefan等研究发现液态水可以密封针孔，消除对流气体的交叉，从而减轻缺陷处的局部膜降解[6].综合上述研究，提出通过掺杂空心微球，吸引裂纹.当空心微球破裂，释放裂尖附近应力场，球内封装的水或修补液可以减缓或阻止裂纹扩展带来的氢气渗透，最终起到提高耐久性的作用.为此，本文通过扩展有限元法研究空心掺杂小球对裂纹的吸引作用，确定能捕捉裂纹的掺杂数量，为掺杂方案提供科学依据.

1 有限元模型

本文采用扩展有限元法(Extended Finite Element Method，XFEM)研究裂纹扩展.通过ABAQUS用户自定义单元实现XFEM计算.材料性质参考杜邦生产的Nafion(115)膜，其弹性模量为E=249 MPa，泊松比ν=0.3；掺杂小球内空心孔半径ΔR=10 μm，整体小球半径R=13 μm，弹性模量ΔE=E，泊松比ν=0.3.考虑膜厚远远小于横向尺寸，本文采用二维模型，实际膜厚127 μm，实验中膜厚设为120 μm，截取横向尺寸为膜厚的2倍.模型加载如图1，上边界施加F=1 MPa的应力，下边界固定，左右两边界自由.不考虑裂纹扩展停止，开裂角的计算采用最大拉应力强度理论计算，强度因子根据相互作用积分得到.计算流程如图2所示.

图1 建模和载荷边界

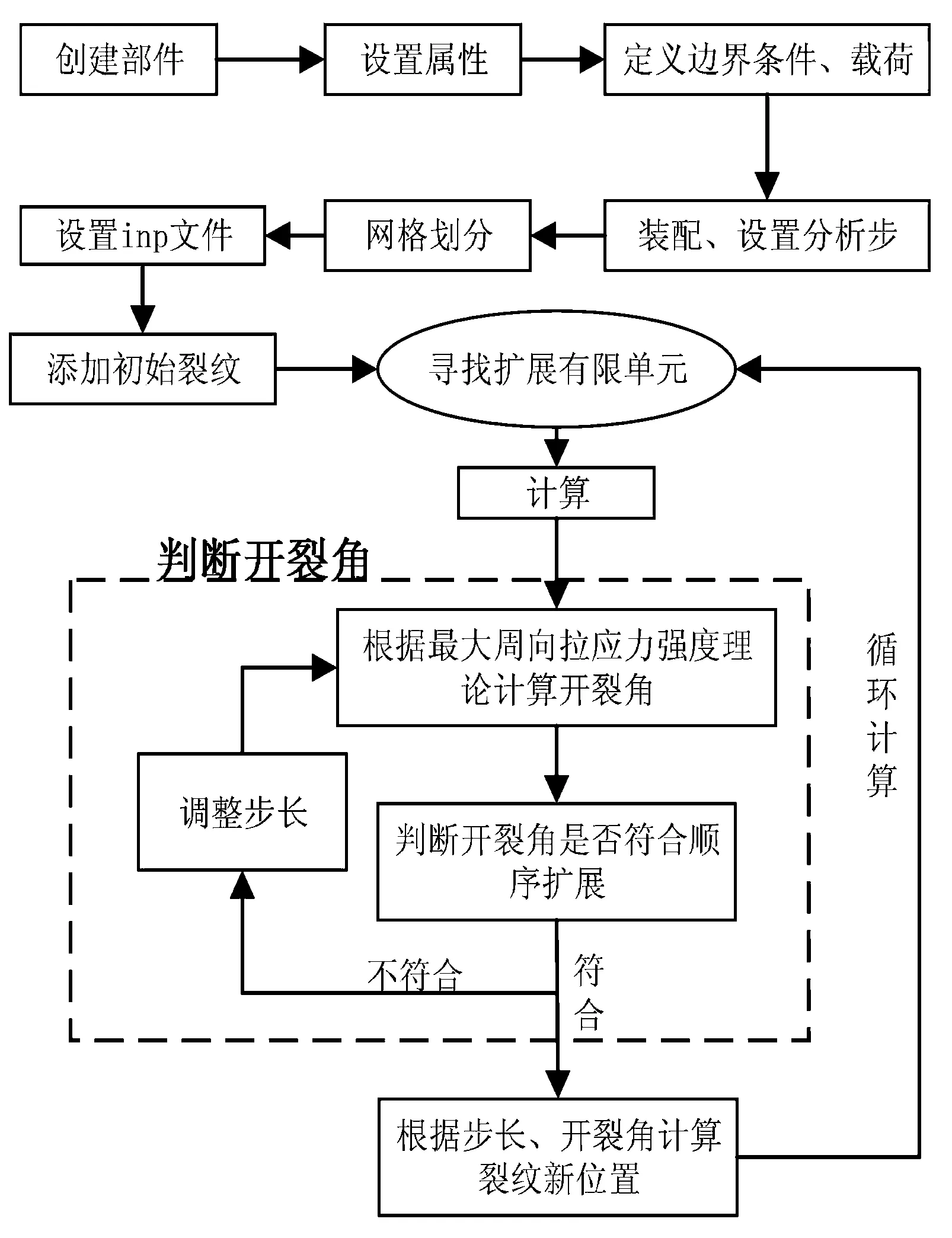
图2 裂纹扩展计算流程图

2 分析和讨论

2.1 单个空心球的影响

与软质实心球对裂纹的影响类似，单个空心球可以吸引裂纹如图3所示.

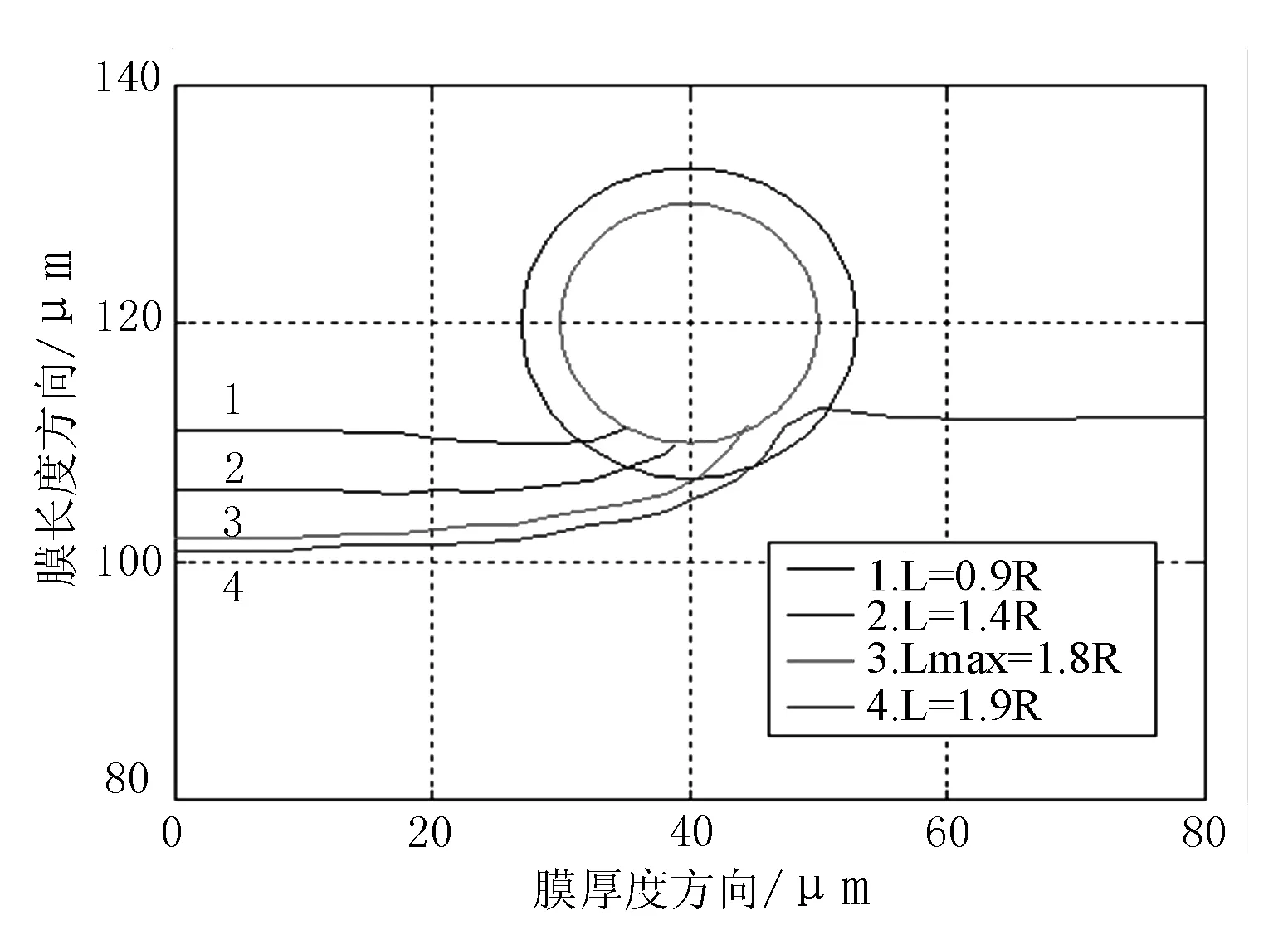
图3 不同裂纹位置扩展路径

计算结果表明，最大横向作用距离为1.7R≤Lmax≤1.9R；最大横向作用距离随空心球半径的增大而增大；空心球壳厚对最大作用距离影响不明显；最大作用距离随膜球之间弹性模量比的增大而增大.

在实际应用中，掺杂小球总是密集分布且分布规律比较复杂，假设掺杂小球分布均匀.首先考虑两个相邻小球对裂纹扩展的影响.

2.2 两个小球水平排列下的裂纹扩展

在膜上同一水平高度放置两个空心球，膜的左下角位于直角坐标系原点，单位μm，设一个球心位置为(40,120)，另一个球心位置为(90,120)，软质球半径R=13 μm，膜球弹性模量E/ΔE=1，距小球中心线L处添加初始裂纹，L的取值范围为0≤L≤2.0R，如图4所示，裂纹扩展路径仿真试验结果如图5所示.

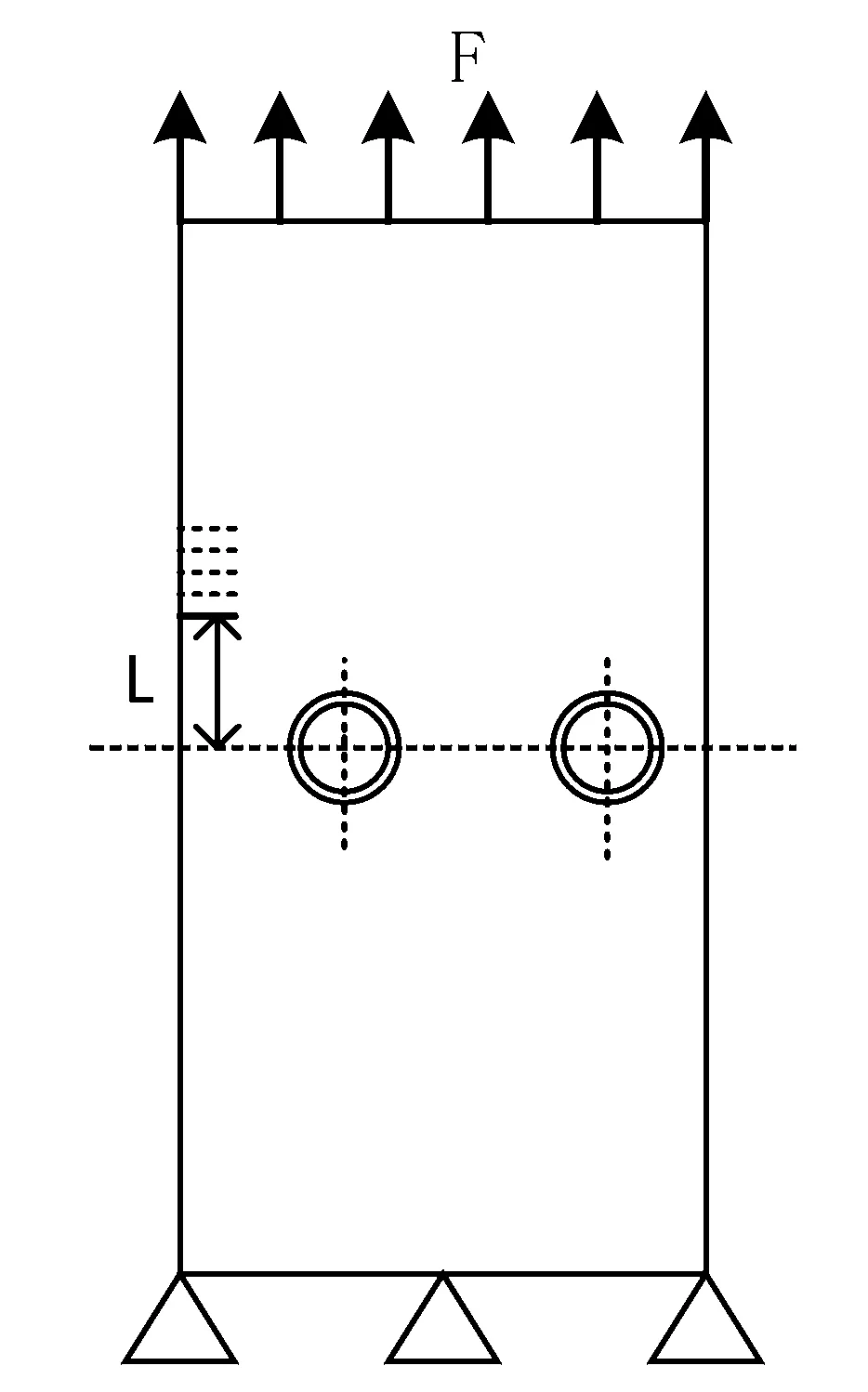
图4 两软质球水平掺杂

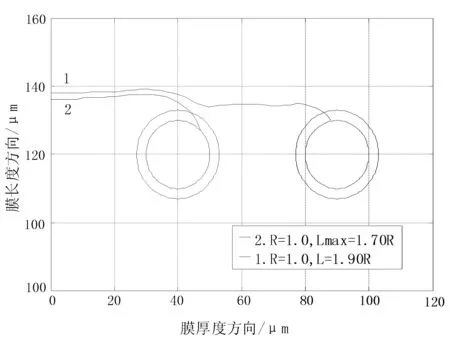
图5 两软质球水平掺杂下裂纹扩展路径

研究发现，对于左边第一个软质球来说，其对裂纹的最大作用距离Lmax仍然符合单一掺杂软质球的结论，但在最大作用距离之外的裂纹如L=1.90R，第一个软质球不能完全“吸引”，但是仍有被吸引的趋势，当到达第二个小球作用区域内，会被第二个软质球“吸引”，同时根据试验可知最大作用距离变为1.90R≤Lmax≤2.10R，在膜厚方向多个小球可以叠加“吸引”作用.

2.3 两小球竖直排列下的裂纹扩展

现在竖直方向排列两个软质球，单位为μm，一个球心位置坐标为(40,120)，另一个位置坐标为(40,180)，其他条件均不变，如图6所示，在不同位置下添加初始裂纹，裂纹扩展路径如图7所示.

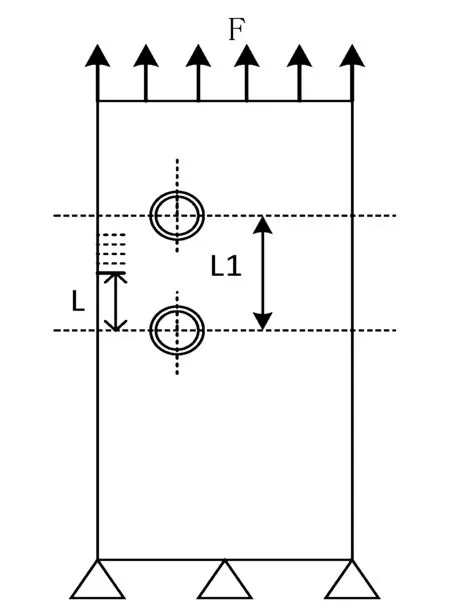
图6 两软质球竖直掺杂

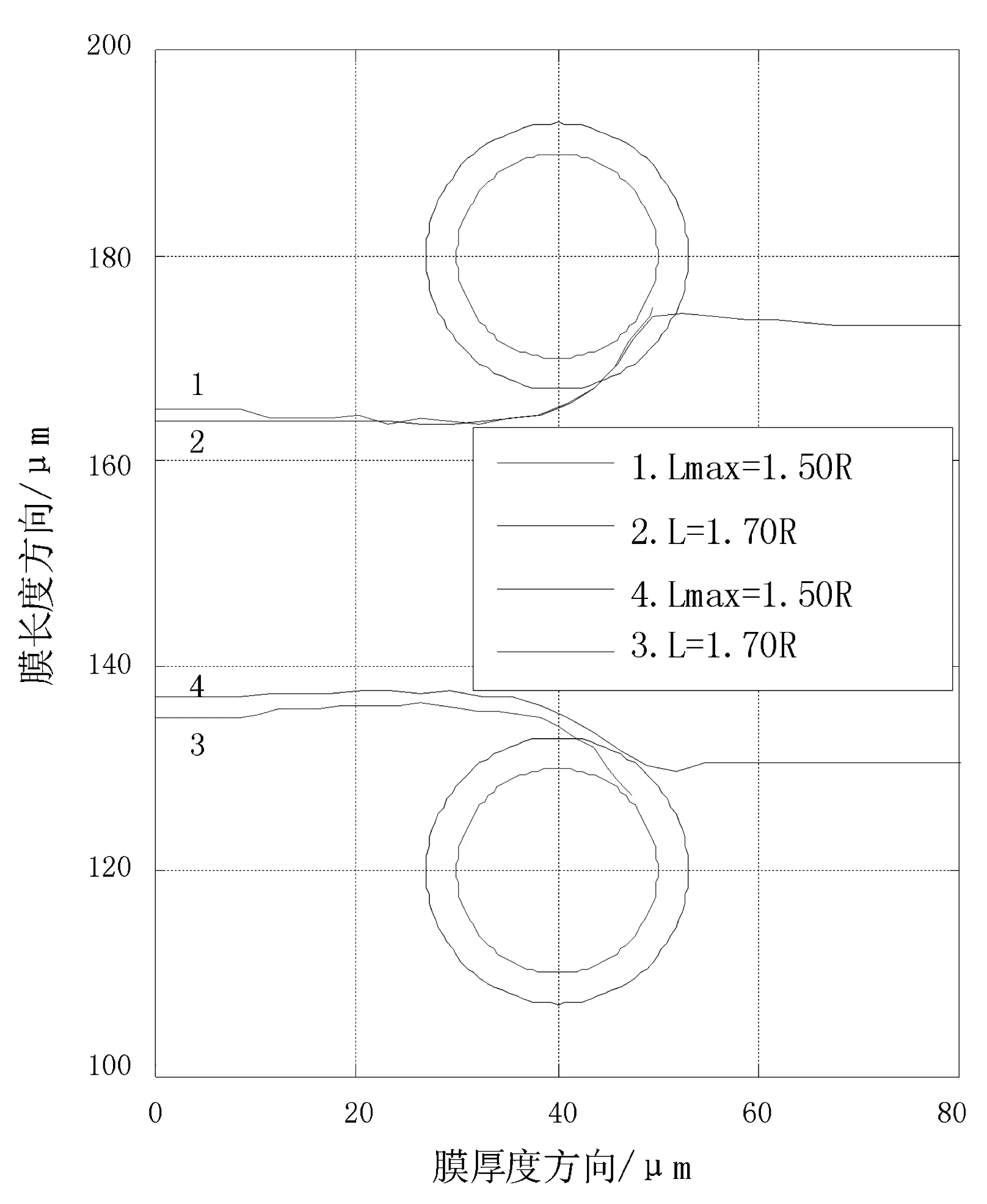
图7 两软质球竖直掺杂下裂纹扩展路径

由仿真试验结果可知，当两软质球竖直排列时，每个小球的最大作用距离Lmax缩小为1.50R左右，这是因为每个空心小球对裂纹都有“吸引”作用，但其对裂纹的“吸引”力作用方向相反，会互相抵消一部分，导致“吸引”能力变差；当改变L1的尺寸时，L1=3.0R～7.0R，每个小球的最大作用距离Lmax仍然为 1.50R左右.

虽然单层排布小球对裂纹的控制起明显有效的作用，但裂纹在两空心球中间位置时，两球对裂纹的“吸引”作用力等大反向，受到两作用力的合力为零，在此区域空心球不能完全控制裂纹，研究发现当采用多层小球排布时，这一缺陷能被优化.

2.4 矩形分布阵列掺杂情况下的裂纹扩展

考虑使用更多个小球分层排列的影响，首先按两层上下排列，膜的整体仍然采用初始模型，边界条件和加载均不变，在膜内排布两层，单位为μm，位置坐标为第一层(40,120)、(40,180)，第二层(70,120)、(70,180).掺杂示意图如图8所示，在不同位置添加裂纹后的仿真试验结果如图9所示.

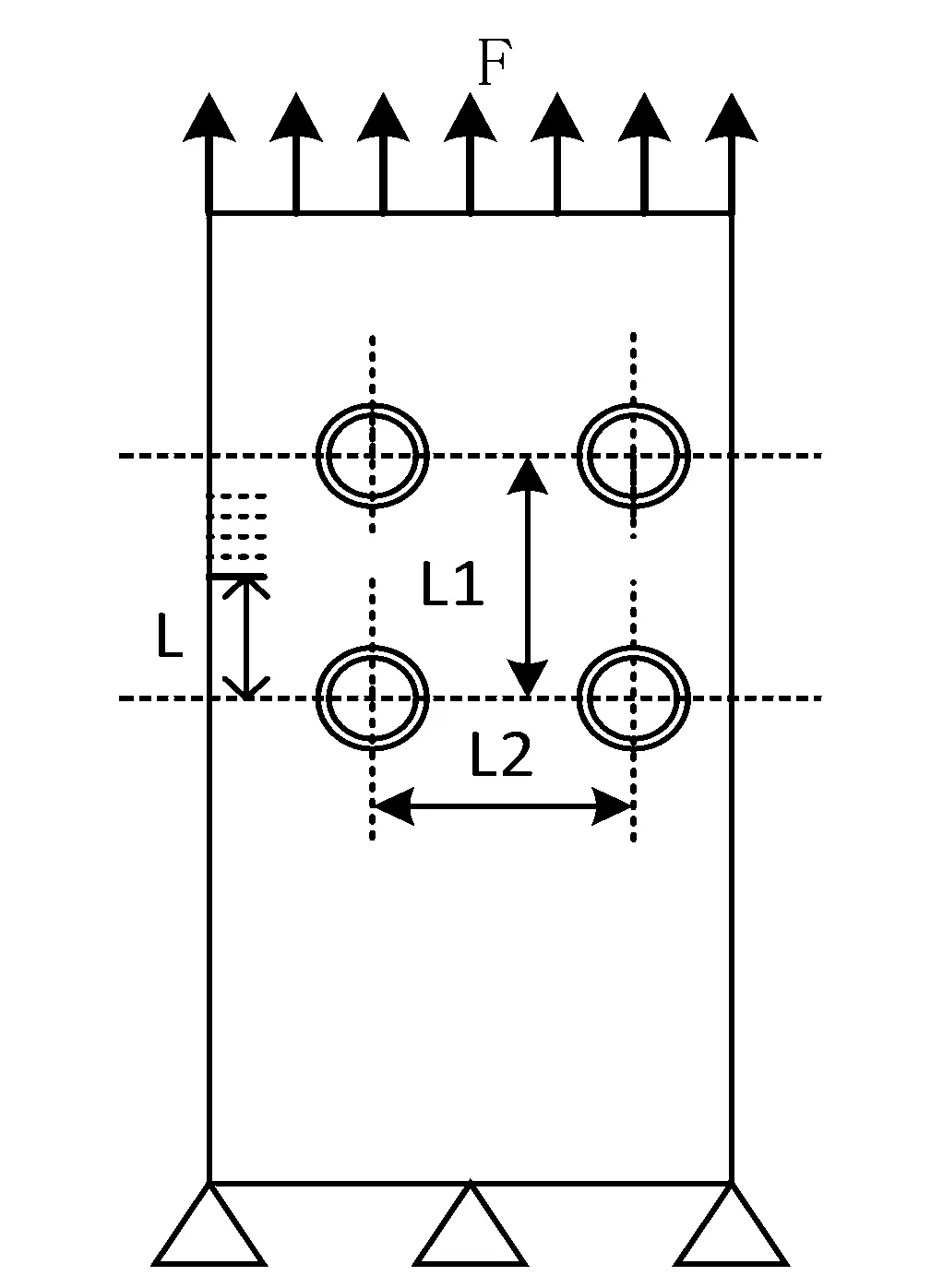
图8 软质球阵列掺杂

图9 软质球阵列掺杂下裂纹扩展路径

在2.3节实验基础下讨论矩形排列分布对裂纹的“吸引”情况，结果表明，在L1=3.0R～7.0R变化的情况下，增加矩形排列小球B、D后，球A、C最大作用距离外的裂纹可以被球B、D控制，相比于2.3节两小球竖直排列每个小球最大横向作用距离有所增大，根据2.2节和2.3节，最有效的间隔距离L1=3.8R，此时每个小球的最大作用距离Lmax=1.9R；但减小L1的长度时，最大作用距离也会适当减小；另外，球AB、球CD之间的距离L2对小球最大作用距离的改变作用不明显，此时取L2=4.0R,第一层小球的“吸引”起主要作用，第二层起辅助作用.

2.5 交错分布阵列掺杂情况下的裂纹扩展

考虑在中间不可控制的部分掺杂一小球，中间的裂纹完全被此小球控制，具体实现如下.在两球中间交错排列一球可以控制两球中间的裂纹，所以膜内软质球最合适的排列方式是分层错位排布，膜的整体仍然采用初始模型，边界条件和加载均不变，在膜内分层错位掺杂软质球，单位为μm，掺杂软质球的位置为第一层(40,120)、(40,180)，第二层(70,90)、(70,150)、(70,210)共五个，掺杂示意图如图10所示，在不同位置添加裂纹后的仿真试验结果如图11所示.

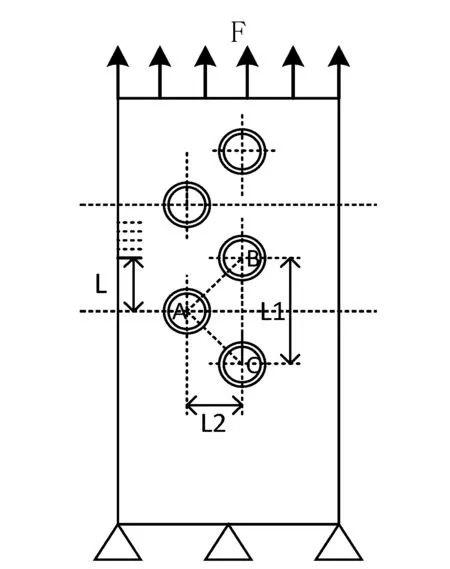
图10 软质球错位阵列掺杂

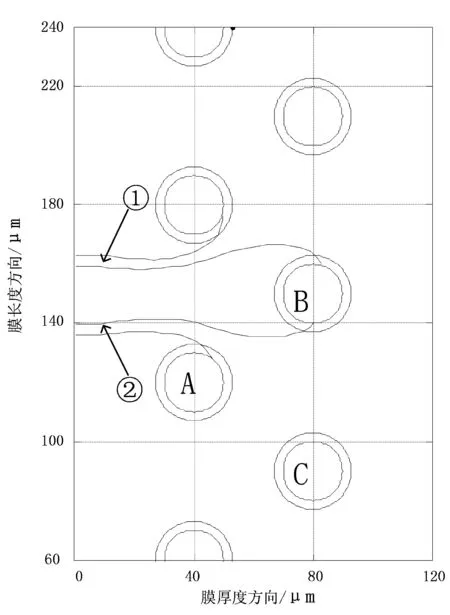
图11 软质球错位阵列掺杂下裂纹扩展路径

研究得知，验证2.4节所得结论并且阵列掺杂后能更有效的控制裂纹，但当小球间距较大时，仍存在裂纹既不能被第一层小球(球A)也不能被第二层小球(球B)吸引的区域，这是因为球A、球C仍对裂纹有“吸引”作用，如图11中①和②.计算表明，阻止裂纹穿透的小球阵列每层中的间隔距离L1=6.0R，考虑实际掺杂情况小球层与层配置下所需的间距L2=3.0R.

3 小球分布数量

对于单层小球阵列分布，根据单个小球对裂纹最大作用距离1.7R≤Lmax≤1.9R，单层分布多个小球，每个小球的最大作用距离Lmax约为1.5R左右，在每层错位分布间隔距离为3.0R,单位面积上(1 mm×1 mm)分布小球约770个；对于两层小球，有两种掺杂方案，矩形分布阵列掺杂排布方式参考图8所示，根据掺杂位置小球间隔距离L1=3.8R, 每层间隔距离L2=4.0R，单位面积上(1 mm×1 mm)分布每层625个空心球，需要排布两层；另一个为错位分布阵列掺杂的方案，小球排布方式参考图10，则在每层内小球间隔距离L1=6.0R，每层间隔距离L2=3.0R，单位面积上(1 mm×1 mm)分布小球约400～440个，这种排布方式需要的空心球数量最少、对膜内质子透过性影响较小、对裂纹的控制程度更可靠.

4 结论

(1)单个空心球可以吸引裂纹，最大横向作用距离为1.7R≤Lmax≤1.9R；最大横向作用距离随空心球的半径增大而增大；空心球壳厚对最大作用距离影响不明显；最大作用距离随膜球之间的弹性模量比的增大而增大.

(2)膜内掺杂软质球最合适的方式是分层错位掺杂，能保证有效降低软质球所占体积比(更有利于质子传导)的同时尽量多的控制裂纹.

(3)试验所参考质子交换膜型号为Nafion(115)，实验表明空心球排布方式最优方案是单位面积(1 mm×1 mm)上错位掺杂排布两层，每层约400～440个，两层间间距为3.0R.