多项式剩余类环中幂零元计数问题研究*

田东代

(山东省菏泽市体育训练中心，山东 菏泽 274000)

1 预备知识

1.1 有限可交换环

有限交换环研究是代数学的基础性工作，主要内容包括唯一性分解问题、准素理想理论和公理化体系等方面[1]，从高次互反律、二元二次型和费马大定理等初等数论问题出发，围绕一系列经典案例展开研究，范围涉及代数数论、代数几何与不变量理论等领域.交换环研究初期以唯一因子分解问题为主，通过对复整数环、理想数等不同代数的精细刻画，提出了理想、序环等概念.E.Noether通过对理想升链条件的深入分析，实现了诺特环的公理化体系，从而建立起一般交换环理论,特别是她给出诺特环(含有限环)的结构分解定理，真正实现了交换环理论体系质的飞跃.在理论发展比较完善之后，其不断提升的理论层次拓宽了它的应用范围，渗透到数学的多个分支，相互间的影响和融合不断促进彼此的创新发展，呈现出未来发展的趋势.

1.2 有限交换环与编码设计

随着20世纪通信技术的快速发展，通信编码技术对交换环理论的依赖日渐显著，具有特殊结构的有限环(域)已成为现代编码理论的核心支撑.经典纠错码如Hamming码、BCH码、RS码等[2,3]在通信和信息领域得到了普遍应用，已成为信息技术领域重要的基础性工作.近年来，移动通信技术的发展也对编码技术提出了更加个性化的要求，具有编码码字多、最小距离大等特点的非线性编码技术成为研究热点 ，促进了有限环上编码技术的实质性进步，极大丰富了纠错码理论的研究领域.

1.3 剩余类环

由于剩余类环中仍保留了欧几里得辗转除法运算，剩余类环中元素具有因子分解特性，不可约多项式判定与零因子、幂零元分类成为有限环中最为重要的两个基本问题.不可约多项式判别方法早期的成果主要是Eisenstein判别法和Berlamkamp[4,5]关于多项式计数的结果，同时也出现了一些确定性判别算法和随机性检测算法，但是都没有一个简单可行的算法思路，至今仍是一件较为复杂的工作.而零因子和幂零元的计数问题则依赖于多项式分解问题，与不可约多项式问题有关联性.

1．4 研究思路与结果

本文利用中国剩余定理，首先给出多项式剩余类环的直和分解，把一般情况下的幂零元问题转化为素数幂阶有限交换环的幂零元问题，再通过定义一般的莫比乌斯、欧拉函数等工具，使用组合反演公式给出幂零元的计数公式，结论刻画思路清晰，表达形式简明统一.

2 基本概念与相关成果

2.1 基本概念

2.1.1 唯一分解概念

没有零因子的交换环结构相对简单，其元素能唯一表示为素元的乘积，称为唯一分解整环，有关研究内容已经十分成熟.具有零因子的交换环则难以给出统一刻画，但仍然可以表示为理想的直和分解.域上的多项式环是整环，每个多项式都可分解成不可约多项式的乘积，两个多项式表示可能相差一个单位元.因此，一般约定不可约多项的首项系数为1 .整数剩余类环Zn[x]上的多项式环中由于系数零因子的存在，多项式表示方式变化增多，虽然仍可以进行欧几里得除法运算，但整环中的唯一分解性不再保留，差异是Zn(模n 剩余类环)中的一个零因子.因此，多项式计数问题需要考虑分解方式的变化，下面从一些概念定义入手，给出Zn[x]中多项式的分解描述.

定义1 设多项式f(x)=anxn+an-1xn-1+an-2xn-2+…+a1x2+a0,式中an,an-1，…，a1,a0∈Zn,那么多项式f(x)的系数公因子定义为整数an,an-1,…,a1,a0的最大公因子gcd(great common divisor)，即有：

gcd(f(x))=gcd(an,an-1，…，a1,a0).

若gcd(f(x))为Zn中的可逆元，则称f(x)为系数公因子等于1的多项式.此时，两个系数公因子相差一个可逆元的多项式被认为是同一多项式.

多项式环Zn[x]中多项式表示的标准形式.

结论1 任意多项式可表示为f(x)=gcd(f(x))f1(x),式中f1(x)是系数公因子等于1的多项式.

证明 假若多项式f(x)有两个不同的分解，f(x)=af1(x)和f(x)=bf2(x).不妨设f1(x),f2(x)是两个不同的系数公因子等于1的多项式，则此时应有a=b，否则按照定义有：

gcd(f(x))=gcd(af1(x))=a·gcd(f1(x))=a·1=a

gcd(f(x))=gcd(bf2(x))=b·gcd(f2(x))=b·1=b

则有a=b，矛盾.

多项式剩余类环Zn[x]/f(x)元素表示的标准形式.

2.1.2 幂零元判别条件

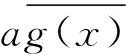
2.1.3 多项式计数函数

我们沿用文献[6]的符号与定义.

定义4[6]若正整数n含有平方因子，则莫比乌斯函数μ(n)的值为零，否则定义为：

定义5[7]设f(x)是多项式环Fp[x]中的n次多项式，定义φ(f)为Fp[x]中次数小于n且与f(x)互素的多项式的个数，并称之为广义欧拉函数.

定义6 广义欧拉函数φ(n,m,d)为Zn[x] 中系数公因子等于d且次数小于m的多项式的个数.

结论2 关于广义欧拉函数φ(n,m,d)有如下结论：

证明 首先Zn[x]中所有次数小于m的多项式总数为nm.另一方面，可根据多项式系数公因子对多项式进行分类，分类数与n的因子个数相同，而每一个分类中元素计数公式为φ(n,m,d)，根据组合分类相加原则得到

证毕.

定理1Zn[x] 中系数公因子等于1且次数小于m的多项式的个数为：

证明引用经典组合反演公式证明.如果有两个整数函数F(u),G(u)满足求和公式

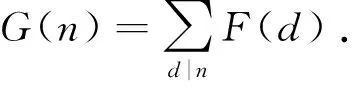
则组合反演公式为

根据组合反演公式可直接得到

推论1 设n=pr,则φ(n,m,1)=pmr-pm(r-1).

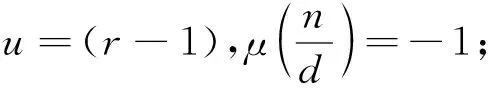
2.2 相关成果

关于域上的多项式剩余类环中幂零元计数问题已得到完整解决，具体如下.

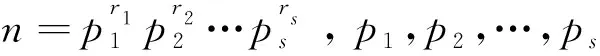
式中φ(n)是欧拉函数.

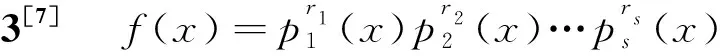
R(f)=pn-t,t=∂(p1(x)p2(x)…ps(x)),

其中∂(g(x))表示多项式g(x)的次数.

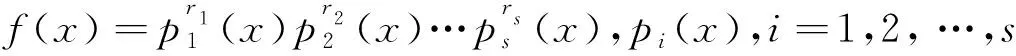
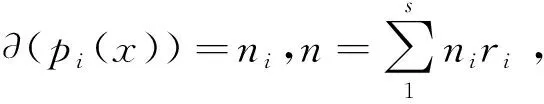
利用此表达式可给出幂零元计数的另外一种形式.

剩余类环Fp(x)/f(x)中幂零元的个数为：

3 主要结果

3.1 直和分解

本节将利用剩余类环中元素分解表示的特性给出具体的直和分解方法，并以此为基础讨论局部环中幂零元的计数问题.

3.1.1Zn的直和分解

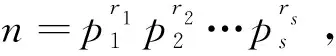
证明 利用中国剩余定理构造环同构映射Ψ.对于Zn中任意元素a，考虑同余方程组：

(1)

3.1.2Zn[x]/(fx)的直和分解

利用结论3同样的方法可得到Zn[x]/f(x)的局部环分解结构.

定理5多项式剩余类环的直和分解为：

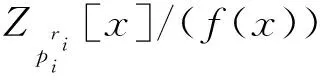
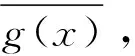
(2)

由此可证同余方程组(2)有唯一解.于是映射Ψ是一一对应.另外，易验证其保持加法和乘法运算，从而得到一个环同构.证毕.

3.1.3Zpr[x]/(f(x))的幂零元计数

设f(x)系数公因子为1的m次多项式.若f(x) 为不可约多项式，则剩余类环Zpr[x]/(f(x))中系数公因子为1的多项式是幂零元的充分必要条件为f(x)的倍式，即零多项式.因此，只考虑可约多项式为模的情况.

引理1 设f(x)系数公因子为1的m次多项式，若f(x)为不可约多项式的方幂，设f(x)=p(x)r，

∂(p(x))=t，则Zpr[x]/(f(x)) 中系数公因子为1的幂零元计数个数为p(m-t)r-p(m-t)(r-1).

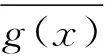
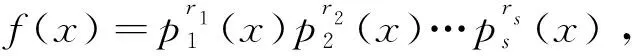
φ(pr,m-t,1)=p(m-t)r-p(m-t)(r-1).

式中t=∂(p1(x)p2(x)…ps(x)).

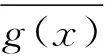
g(x)=p1(x)p2(x)…ps(x)g1(x)，

4 结语

本文构造了多项式剩余类环的局部直和分解，将剩余类环中幂零元计数问题归约为局部环中的计数问题，给出了具体计数表达式.所采用的代数分析思路与组合函数计数考虑虽源于传统经典组合论内容，但也充分利用了多项式可整除性，融合了一些巧妙的论证技巧，方法上的创新性对于有限局部环特殊元素计数问题具有一定的借鉴作用，尤其是对于有限局部环上编码理论的研究有着重要的积极意义.