基于IGC规则的C型液货舱参数化设计方法

黄国良,郑坤,牛志刚,孙冰,奉宁琛

(1.中海油能源发展股份有限公司 采油服务分公司，天津 300452;2.大连理工大学 船舶工程学院，辽宁 大连 116023)

C型液货舱广泛应用在中小型LNG运输船、加注船等船舶上。在这些布置型船舶的前期方案设计中，C型液货舱的设计往往主导着后续的主尺度设计和总布置设计，是整个设计过程的核心。C型液货舱设计的优劣也通常决定着船舶整体性能的优劣。IMO发布的《国际散装运输液化气体船舶构造和设备规则》[1](以下简称《IGC》规则)中对C型液货舱的设计和计算有详细的介绍。

相关研究[2-5]仅将有关计算规范与C型液货舱进行了简单的对应，无法高效地进行C型液货舱设计。为此，提出一种基于IGC规则的C型液货舱参数化设计方法，将C型液货舱的几何结构特征描述成数学函数，通过改变特征参数进行参数化设计，由此可得到容量和结构承载能力满足要求，重量最轻的方案。

1 C型液货舱设计

1.1 C型液货舱参数化设计

要进行C型舱的尺寸设计，必须先确定货舱体积和几何尺寸之间的关系，并求出相应的数学表达式。下面分别讨论3种液货舱的货舱体积和几何尺寸之间的关系。

如图1、2所示，单体型体积Vd和双体型体积Vs为

图1 单体型液货舱

(1)

(2)

式中：R为球形封头半径，m；L为筒体长度，m；D为双筒体中心距，m。

图2 双体型液货舱

如图3所示，3体型液货舱几何特点较为复杂，需分别考虑筒体部分和封头部分。

图3 3体型液货舱

筒体部分的体积表达式Vcy为

(3)

两端封头部分拼接后，可以看成是由3个球体组成，相交部分见图4，分为球体两两相交的部分(浅色)和3个球体相交的部分(深色)。

图4 3球相交示意

封头体积用Vhead表示，球体两两相交的部分，分为下部两个球体相交部分(体积V11)、上部球体和下部球体相交部分(体积V12)和3个球体相交部分(体积V2)。

Vhead=4πR3+2V2-2V12-V11

(4)

球体两两相交部分体积由几何关系容易求得，3个球体相交的部分，采用数值计算方法，见图5。

图5 相交部分沿水平划分示意

1.2 C型液货舱板厚设计

1.2.1 舱体板厚计算原理

根据《IGC规则》，筒体板厚t为

(5)

球形封头板厚t为

(6)

式中：t为计算板厚，mm；peq为设计压力，MPa；Di为液罐内径，m；σm为许用应力，MPa；Φ为焊接效率系数,可取1；c为腐蚀增量，mm。

其中设计压力peq主要考虑内部蒸汽压力p0和船舶运动引起的动载荷pgd。

(7)

式中：αβ为在任意的β方向上，由重力和动载荷引起的无因次加速度，m/s2；Zβ为从所决定的压力点沿β方向向上量至液货舱壳板的最大液柱高度，m；ρ为液货密度，kg/m3。

根据文献[3]中三向加速度椭圆法和二向加速度椭圆法pgd的计算比较，采用二向加速度椭圆法计算pgd。

根据《IGC规则》，对于C型液货舱筒体部分，采用“横向+垂向”二向加速度椭圆法计算；对于球形封头部分，采用“横向+垂向”和“纵向+垂向”二向加速度椭圆法分别计算，取两种方法计算所得的较大值作为计算点的板厚。

1.2.2 舱体板厚计算实现

板厚计算的关键在于pgd的计算，而pgd值与计算点的位置有关。因为计算点的位置是一个连续的变量，若要得出板厚的分布表达式十分困难且没有必要。所以在方案设计阶段，分角度对若干个点进行pgd计算，得出板厚的大致分布，最后通过平均板厚×表面积的方法估算C型舱质量。

下面分为筒体部分、封头部分和水密舱壁，分别讨论pgd和平均板厚的计算方法。

1)筒体部分。对筒体部分分别计算以下角度的pgd：15°,45°,75°,105°,135°,165°

①单体型液货舱。如图6所示，只需计算所示6个点的pgd，结合p0值然后按照等权平均值的计算方法算出6个点的平均板厚，作为筒体部分的平均板厚。

图6 单体型液货舱筒体部分计算点

②双体型液货舱。双体型液货舱计算点的坐标分布和单体型类似，但是双体型筒体上下部分(图7中15°,45°,135°,165°位置点)有内外双侧舱体，而中间部分(图7中75°,105°位置点)只有外侧舱体。所以在计算平均板厚时，需要通过将上下部分的平均板厚×2的方式加大上下部分的权重。

图7 双体型液货舱筒体部分计算点

③三体型液货舱。如图8所示，因为其左右对称，所以只需要计算一半的板厚分布即可。但其上下不对称，所以需要通过将下面部分的平均板厚的方式加大下部的权重。

图8 三体型液货舱筒体部分计算点

2)球形封头部分。对球形封头部分分别计算以下角度的pgd：10°,30°,50°,70°,90°,110°,130°,150°,170°

①单体型液货舱。

a.“纵向+垂向”二向加速度椭圆法计算pgd。由pgd的计算公式可知计算pgd的关键在于计算出αβ和Zβ的值。规则给出了αβ明确的计算公式，且与舱型、加速度椭圆法无关。故这里重点在于得出Zβ的计算公式。

如图9所示，以30°处为例，在β1和β2下，对应的Zβ分别为图中所示的Zβ1和Zβ2，其中Zβ左端的点为计算点，右端的点为与封头圆的切点。根据图中的几何关系得到Zβ的计算式如下。

图9 单体型封头“纵向+垂向”法计算点

Zβ=(1+cosβ)·R+Lsinβ+xsinβ-zcosβ

(8)

式中：βj为“纵向+垂向”的合成加速度矢量角；x、z为计算点的垂向和纵向坐标的绝对值。

以此方法可计算出9个计算点的Zβ，进而可以计算出相应的pgd。

b.“横向+垂向”二向加速度椭圆法计算pgd。如图10所示，要用“横向+垂向”二向加速度椭圆法计算150°处的pgd，可以先用“横向+垂向”法算出右圆105°、35°和165°处的pgdc，然后取3个pgdc中的最大值，即可作为球形封头150°处的pgd。这种方法是偏于安全的。计算过程与单体型液货舱筒体部分的pgd计算相同，30°处pgd则用15°、45°和75°处的pgdc进行计算。

图10 单体型封头“横向+垂向”法计算点

10°和170°、50°和130°、70°和110°处的计算，与30°和150°处的计算同理；90°处的pgd，取用“纵向+垂向”法算得的值。由此可以得出用“横向+垂向”二向加速度椭圆法计算得到的9个pgd。

最后用于计算板厚的9个pgd，每个都取“横向+垂向”法和 “纵向+垂向”法算得的相应值中的较大值。最后用9个pgd算得的板厚值进行平均，作为球形封头的平均板厚。

②双体型液货舱。双体型液货舱封头部分的计算与单体型的计算相似。

③三体型液货舱。由于三体型液货舱封头部分几何结构比较复杂，故采用近似计算方法。如图11所示，将三体型液货舱封头部分看成是半径为R1的单体型液货舱封头，这样就能采用单体型液货舱的“纵向+垂向”法计算公式计算三体型液货舱的封头，即

图11 三体型封头“纵向+垂向”法计算点

Zβ=(1+cosβ)·R1+Lsinβ+xsinβ-zcosβ

(9)

由此方法计算出9个计算点的Zβ，然后得出相应的pgd。

如图12所示，因为在横向上有水密舱壁，所以用“横向+垂向”二向加速度椭圆法计算时，可将三体型的3个球形封头部分，分别近似当作单体型的球形封头来计算。需要注意的是，因为三体型液货舱上下不对称，所以在计算平均板厚时需要加大下部的权重。

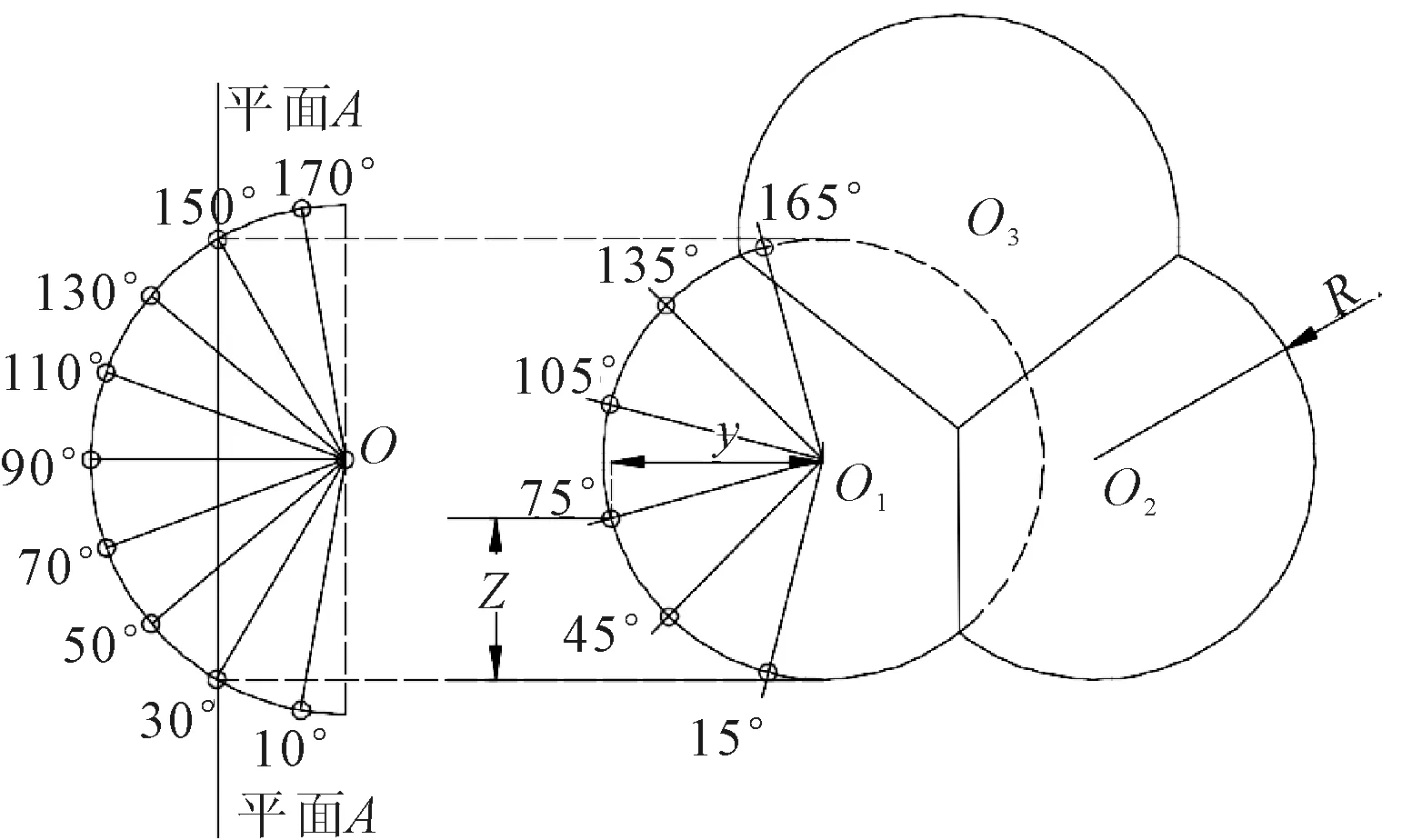
图12 三体型封头“横向+垂向”法计算点

3)水密舱壁部分。根据《IGC规则》，液货罐水密纵舱壁板厚度t，应满足下式要求。

t≥(2peq·e)/(20σmΦ-peq)+c

(10)

式中：e为双体罐的轴心距，mm；其余符号的意义与筒体部分和球形封头板厚计算公式中相同。

同球形封头一样，需要得出Zβ的计算式。单体型液货舱无水密纵舱壁，故只需要考虑双体型和三体型液货舱，并假设水密舱壁板为1块厚度不变的板。

①双体型液货舱。见图13可得

图13 双体型液货舱水密舱壁计算点

(11)

由Zβ计算式可知，pgd随垂向坐标z的增大而减小，故计算点应选择水密舱壁板的最低点，保证计算结果偏于安全。

图14 三体型上部水密舱壁计算点

(12)

因为Zβ的值正负不定，故pgd的值随横向坐标y的改变而大小不定。此处沿垂向取9个计算点，计算这9点的pgd，最后取最大值作为计算板厚的参考值。

2 算例

以液货舱重量最轻为衡量标准，结合“网格法”的设计方法和前述基于IGC规则的C型舱参数化设计方法得到C型舱的设计流程，见图15。根据设计流程对一实船的C型舱进行设计和计算，实船的船型主尺度信息见表1。

图15 C型舱设计流程

表1 实例船型主尺度

此船有4个货舱，要设计1个8 000 m3的双体C型液货舱，作为2号货舱(从船艉到船艏数第2个货舱)。舱体的尺寸需要满足表2所示的限制条件。

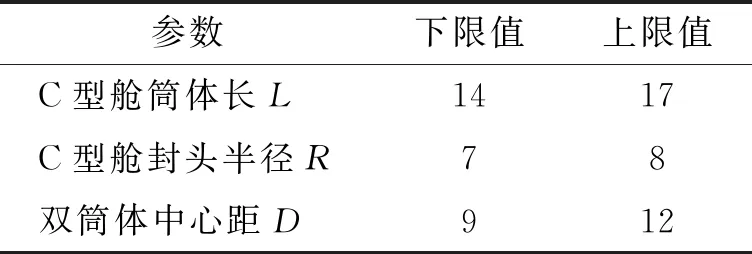
表2 双体型液货舱设计条件 m

用“网格法”生成5个尺寸方案后，选择9%Ni钢作为舱体材料进行板厚设计，最后算得货舱部分板厚分布、舱体重量见表3。由表3结果可知，在满足容积和货舱尺寸的限制条件的情况下，方案5的货舱重量最轻，为最佳方案。

表3 板厚分布(部分)和舱体质量

3 结论

通过本文方法的应用，可实现C型舱设计方案快速生成、C型舱舱体板厚及重量快速计算，可有效提高C型舱设计效率，为C型舱方案的优化提供基础。

本方法在后续研究中可考虑与LNG船舶主尺度设计、总布置设计方法相结合，进一步应用于船型方案优化，提升船舶总体设计效率。