某型无人机滑跑起降纠偏控制改进分析

史红伟，蔡永恒，李新华，2

（1.中国航天空气动力技术研究院彩虹无人机科技有限公司，北京100074）

（2.北京航空航天大学航空科学与工程学院，北京100191）

0 引 言

随着无人机的发展与广泛应用，全自主飞行已成为相对成熟的技术，但是对于无人机地面滑跑阶段的研究，包括侧风干扰分析与纠偏控制参数设计等，仍普遍采用外场试验手段，显著增加了系统研发成本和研制周期［1］。地面滑跑阶段的受力模型与空中飞行阶段的受力模型相比更加复杂，尤其是地面滑跑过程中需要考虑轮胎的纵向摩擦力、侧向力、支反力及其力矩的作用，因此建立准确的地面滑跑模型，对于无人机滑跑起降动力学特性的研究以及纠偏控制律的设计优化具有重要意义［2-3］。

现有研究已对无人机地面滑跑起飞过程进行了相对充分的研究和分析，例如，王勇等［4］基于无侧向滑动假设建立了包括起落架和刹车装置的无人机滑跑数学模型以及主动刹车和方向舵纠偏的控制模型；李洁玉等［5］基于轮胎侧向力模型和刚性全机假设建立了高速无人机的全量非线性滑跑数学模型以及方向舵纠偏的控制模型；马振宇等［6］基于轮胎侧向力模型和弹性轮胎模型建立了全翼布局太阳能无人机全量非线性滑跑数学模型以及螺旋桨动力差动的纠偏控制模型；Dong Sun等［7］运用动态分配增益算法进行前轮与差动刹车主动控制；Li Bo等［8］基于轮胎滑移模型以及无侧向滑动假设分析了飞机以及轮胎的响应情况。上述研究或在研究对象方面没有考虑螺旋桨无人机的发动机扭矩对滑跑的影响，或针对起飞和着陆滑跑阶段不同的动力学特性综合分析研究较少。

本文在上述相关研究的基础上，针对某型无人机的技术特征，从工程实践出发，忽略起落架弹性压缩带来的附加影响，仅考虑轮胎的弹性变形，并将全机其他部分视为刚体分析［9-11］；在Matlab平台建立地面滑跑阶段全量非线性六自由度动力学模型，研究无人机滑跑起飞和着陆过程的纠偏性能，针对螺旋桨发动机的扭矩干扰和常见的垂直侧风干扰情况进行仿真分析，并对比分析采用前轮转向、主轮差动刹车和方向舵的混合纠偏控制模型与采用前轮转向和方向舵的联合纠偏控制模型下的响应特性。

1 滑跑起降动力学模型

1.1 无人机对象

某型无人机采用鸭式、双垂尾、翼身融合气动布局，主翼采用后掠组合梯形翼并配置副翼，鸭翼后缘配置升降舵，垂尾后缘配置方向舵，一台活塞发动机布置在机身后端并配置三叶推进式螺旋桨，起落架采用前三点布局，主起落架为固定板簧形式，前起落架采用弹簧式缓冲形式并可收放。发动机与螺旋桨采用左旋推进式布局，即从后往前看螺旋桨逆时针方向旋转，因此发动机会对机体产生顺时针方向的扭矩干扰。无人机示意图如图1所示，其主要技术参数如表1所示。

图1 无人机示意图Fig.1 UAV schematic diagram

表1 无人机主要技术参数Table 1 UAV main technical parameter

1.2 机体质心动力学模型

机体坐标系下的质心动力学方程如下：

式中：F Gix，F Giy，F Giz分别为地面对轮胎三个方向的作用力分量；L ba为气流坐标系到机体坐标系的转换矩阵；L、D、C分别为升力、阻力和侧力，其中升力向上为正，阻力向后为正，侧力指向机体右侧为正。

1.3 机体绕质心转动动力学模型

根据动量矩定理可以得到机体坐标系下三自由度转动方程：

式中：M x，M y，M z分别为作用在无人机上的发动机推力、气动力和轮胎作用力所构成的合力矩。

1.4 机体质心运动模型

地面坐标系下的机体质心运动学方程为

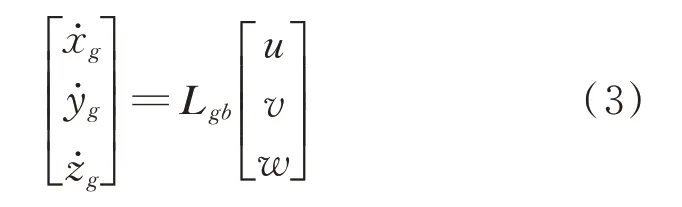
式中：L gb为机体坐标系到地面坐标系的转换矩阵。

地面坐标系下的机体转动运动学方程为

1.5 轮胎地面受力模型

轮胎地面受力分析情况如图2所示。

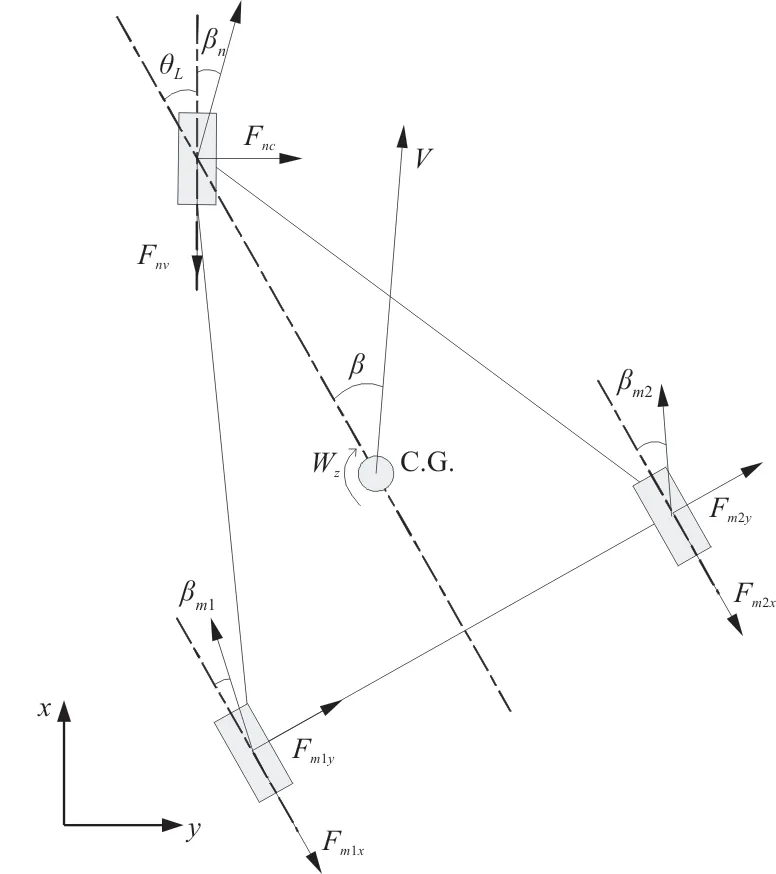
图2 轮胎地面受力情况示意图Fig.2 Ground force acting on wheels

轮胎受到的地面纵向摩擦力为［12-13］

式中：μ为轮胎滚动摩擦系数；P为轮胎支反力；M为刹车力矩；R为轮胎半径。

轮胎受到的地面侧向力方程相对复杂，本文采用如下形式［12-13］：

式中：k为侧力系数；β为侧偏角，是轮胎速度方向与轮胎对称面的夹角。

轮胎支反力是轮胎压缩量的函数，可表示为［14-15］

式中：CT为轮胎垂直振动阻尼系数；f（δ）为轮胎静压曲线，一般由轮胎实验确定；δ为轮胎压缩量。

三个轮胎的压缩量计算公式为

三个轮胎的压缩速度为

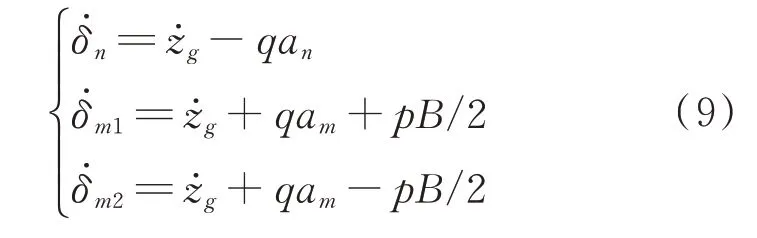
式中：an为前轮到机体重心距离；am为后轮到机体重心距离；B为主轮距。

2 起降纠偏控制律模型

无人机当前地面滑跑阶段采用前轮转向、主轮差动刹车和方向舵混合纠偏控制形式，根据长期使用效果来看，由于起飞阶段差动刹车量控制介入过多，导致起飞滑-跑距离偏长。该混合纠偏控制模型如下：

前 轮 转 向=0.1×dZ+0.2×dPsi，限 幅±1.5°。

方 向 舵=-2×dZ-3×dPsi+1×Wy，限幅±8°。

差动刹车量=3.5×dZ+4×dPsi，起飞阶段基础量为0%，差动量限幅25%；着陆阶段基础量为40%，差动量限幅10%。

其中，dZ为侧偏距（m）；dPsi为偏航角（°）；Wy为偏航角速度［（°）/s］。

针对滑跑距离进行优化的纠偏控制模型起飞阶段默认采用前轮转向和方向舵的联合纠偏形式，只有在满足下列条件之一时，才会接入主轮差动刹车并且不再退出；着陆阶段控制模型保持不变。

（1）侧偏大于4 m；

（2）地速大于9 m/s，且航向角大于5°。

优化后的起飞阶段纠偏控制模型如下：

前轮转向=1×dZ+0.8×dPsi，限幅±4°。

方 向 舵=-2×dZ-3×dPsi+1×Wy，限幅±8°。

差动刹车量=5×dZ+4×dPsi，起飞阶段基础量为0%，差动量限幅25%。

3 仿真验证

3.1 自由滑跑起降

为了验证仿真模型本体的正确性，首先进行无控状态的自由滑跑起飞和着陆仿真，其中起飞仿真阶段以地速为0时为起点，终止于主轮离地；着陆仿真阶段以地速35 m/s时为起点，终止于地速降为0；同时起飞过程中左右主轮刹车基础量均置为0%，着陆过程中左右主轮刹车基础量均置为40%。仿真响应曲线如图3～图4所示。

图3 无控状态自由滑跑起飞仿真Fig.3 Free taxiing during takeoff

图4 无控状态自由滑跑着陆仿真Fig.4 Free taxiing during landing

从图3～图4可以看出：当不考虑发动机扭矩、侧风等外界干扰因素时，无人机只有纵向运动，没有侧向运动，仿真模型可以正确地反映真实滑跑情况。

3.2 考虑发动机扭矩情况的自由滑跑起飞

起飞过程中发动机顺时针方向的扭矩会对机体产生持续的滚转力矩干扰，着陆过程由于发动机处于停车状态，不必考虑发动机扭矩情况。仿真响应曲线如图5所示。

图5 考虑发动机扭矩情况的滑跑起飞仿真Fig.5 Free taxiing responding to piston engine torsion during takeoff

从图5可以看出：起飞过程无人机右主轮所受的地面支反力大于左主轮，以平衡发动机扭矩对机体产生的右滚转力矩，从而右主轮纵向摩擦力大于左主轮；在纵向摩擦力产生的右偏航力矩作用下，无人机逐渐向右偏转，在此过程中前轮受到的侧向力大部分为负，主轮所受的侧向力全程为正；外部表现为无人机向右侧滑跑，且随时间增加侧偏逐步偏大，与实际趋势相符。

3.3 考虑侧风情况的自由滑跑起降

引入2 m/s的常值左侧风以及发动机扭矩，仿真响应曲线如图6～图7所示。其中侧风方向垂直于跑道方向，起飞阶段从地速为0时刻开始施加，着陆阶段以地速35 m/s时刻开始施加，直至仿真结束。

图6 考虑侧风和发动机扭矩情况的滑跑起飞仿真Fig.6 Free taxiing responding to crossw ind during takeoff

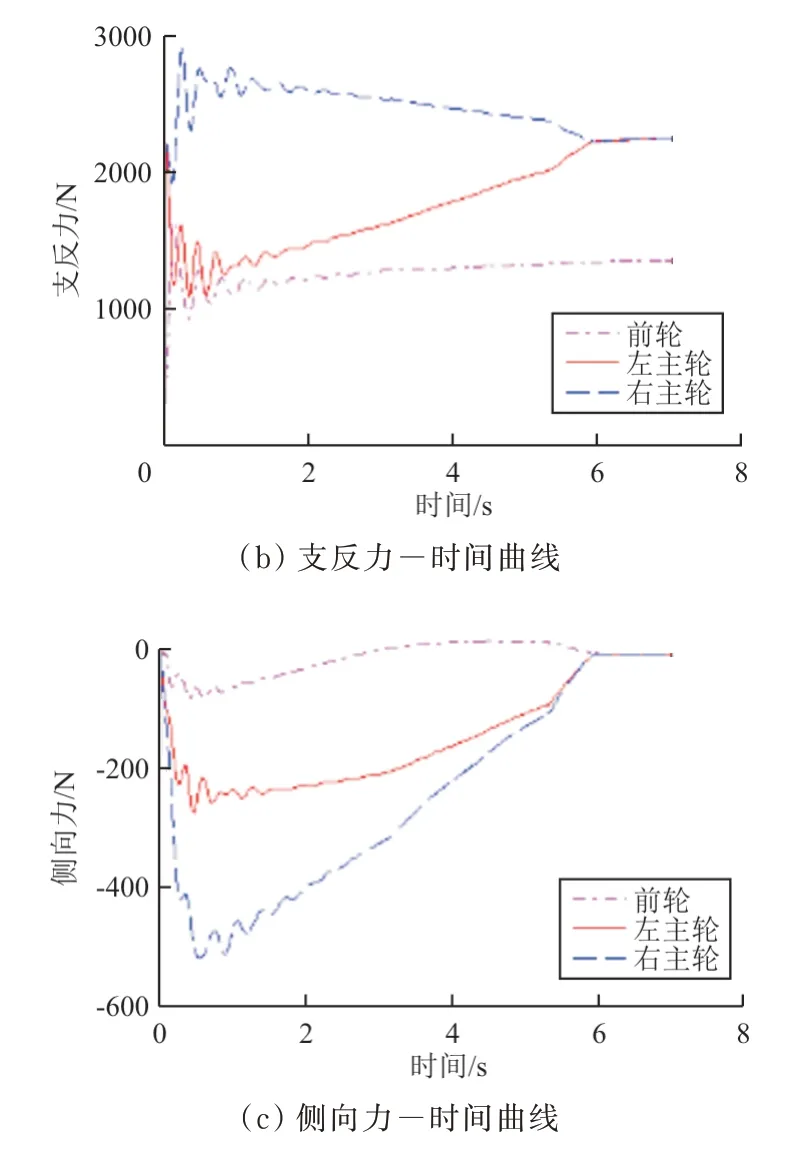
图7 考虑侧风情况的滑跑着陆仿真Fig.7 Free taxiing responding to crosswind during landing

从图6可以看出：起飞过程无人机右主轮所受支反力大于左主轮，以平衡发动机和侧风产生的右滚转力矩，故右主轮纵向摩擦力大于左主轮；同时在侧风产生的左偏航力矩作用下，无人机逐渐向左偏转，在此过程中前轮受到的侧向力大部分为正，主轮所受的侧向力全程为负；外部表现为无人机向左侧滑跑，且随时间增加侧偏逐步偏大。结合图5可以看出，发动机的扭矩减弱了左侧风状态下的侧偏趋势，但总体上仍不及左侧风影响程度大。

从图7可以看出：着陆过程无人机在左侧风作用下，右主轮所受支反力大于左主轮，在侧风产生的左偏航力矩作用下，无人机逐渐向左偏转；外部表现为无人机向左侧滑跑，在刹车的作用下地速快速降低，侧偏最终稳定在-10 m左右。

3.4 原控制律状态滑跑起降

原控制律状态采用前轮转向、主轮差动刹车和方向舵的混合纠偏控制模型。以左侧风8 m/s为例，仿真响应曲线如图8～图9所示。

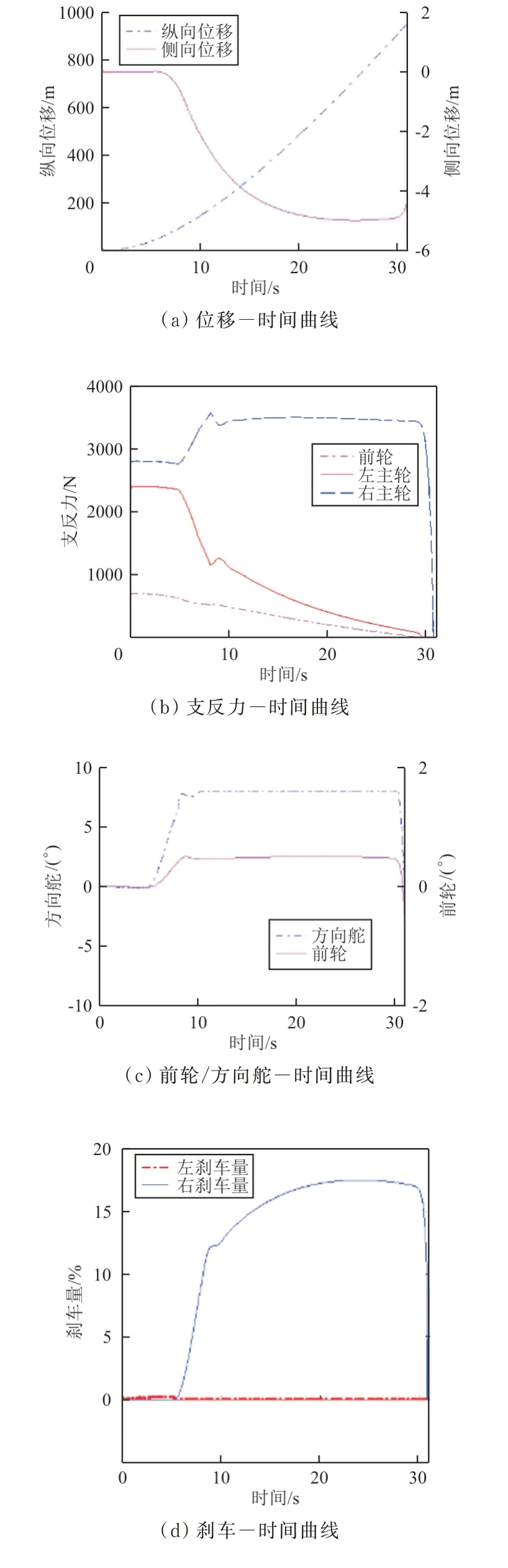
图8 原控制律状态滑跑起飞仿真Fig.8 Lateral-rectification-control taxiing during takeoff

图9 原控制律状态滑跑着陆仿真Fig.9 Lateral-rectification-control taxiing during landing

从图8可以看出：起飞过程在左侧风以及发动机扭矩作用下，无人机右主轮所受支反力大于左主轮，同时无人机逐渐向左偏转；在纠偏控制的作用下，前轮输出右转向角，以纠正机头的左转趋势，同时方向舵右偏和右主轮差动刹车，以产生右偏航力矩，在三者的综合作用下，侧偏逐步收敛至-4 m，期间最大侧偏为-5 m。

从图9可以看出：着陆过程在8 m/s左侧风作用下，无人机右主轮所受支反力大于左主轮，同时无人机逐渐向左偏转；在纠偏控制的作用下，前轮输出右转向角，方向舵右偏和右主轮差动刹车，以产生右偏航力矩，侧偏逐步收敛在-3 m，期间最大侧偏为-4.6 m。

针对不同的侧风情况进行仿真分析，无人机在混合纠偏控制系统作用下的起飞和着陆最大侧偏如图10所示。

图10 不同侧风条件下的起飞和着陆最大侧偏Fig.10 Lateral deflection under different crosswind

从图10可以看出：起降过程中最大侧偏与侧风大小基本呈线性变化规律，8 m/s侧风情况下的最大侧偏为5 m，同时起飞过程在左侧风和右侧风情况下发动机扭矩因素的影响不甚明显，且着陆阶段抗侧风能力稍大于起飞阶段。

3.5 优化控制律状态滑跑起飞

优化控制律状态采用前轮转向和方向舵的联合纠偏控制模型。以左侧风8 m/s为例，仿真响应曲线如图11所示，可以看出：在左侧风作用下，前轮输出右转向角，同时方向舵右偏，以纠正机头的左转趋势；在左侧偏达到4 m之后，右主轮差动刹车控制介入，此后左侧偏最大达到8.2 m后快速回正。

图11 优化控制律状态滑跑起飞仿真Fig.11 Optimized lateral-rectification-control taxiing during takeoff

以左侧风情况为例，汇总各侧风工况下的起飞距离与侧偏参数，并与原控制律状态对比，如图12所示。

图12 起飞滑跑距离与最大侧偏情况对比Fig.12 Takeoff distance and lateral deflection comparation

从图12可以看出：由于针对滑跑距离进行优化的控制律对刹车量使用时长缩短，起飞滑跑距离大幅降低，左侧风8 m/s情况下可有效降低43%，与此同时最大左侧偏达到8.2 m，相比增加78%，但仍可以较好地实现纠偏控制。

4 结 论

（1）基于轮胎侧向力模型、弹性轮胎和刚性机体假设建立的全量非线性六自由度滑跑模型，能够较好地反映无人机滑跑阶段的动力学特性并可验证分析纠偏控制律模型。

（2）顺时针方向发动机扭矩会减弱左侧风状态下的侧偏趋势，并加大右侧风状态下的侧偏趋势，但是总体影响程度有限。

（3）采用前轮转向、主轮差动刹车和方向舵的原混合纠偏控制模型可以对无人机滑跑过程进行有效控制，起降过程中最大侧偏与侧风大小基本呈线性变化规律，在8 m/s侧风情况下最大侧偏为5 m。经统计原控制律状态下实际滑跑最大侧偏与侧风大小基本呈线性变化规律，8 m/s侧风情况下的最大侧偏不超过5 m，与本文仿真结果基本一致，因此将8 m/s侧风作为极限侧风条件。

（4）针对滑跑距离进行优化的前轮转向和方向舵的联合纠偏控制模型，在缩短滑跑起飞距离方面具有较大优势，在侧偏控制方面仍可以较好地实现纠偏控制，足以保证最低30 m宽跑道滑跑起降的安全性。

（5）该无人机依靠前起落架弹簧和主起落架支柱弹性变形耗散能量，而非传统的油液式缓冲器形式，因此建模时对起落架进行了简化，同时着陆纠偏控制阶段发生在着陆冲击之后，剔除起落架变形因素对仿真分析结果不会产生较大影响。

（6）本文通过理论仿真分析为型号研究提供相关参考，由于试验手段限制尚未能开展全部试验参数的测量工作，这也是本文研究的不足之处。后续将深入开展实际滑跑试验数据与理论仿真数据的对比分析工作，进一步验证仿真结果的正确性、可信性。