基于深度确定性策略梯度算法的战机规避中距空空导弹研究
2021-06-28宋宏川詹浩夏露李向阳刘艳
宋宏川,詹浩,夏露,李向阳,刘艳
(1.西北工业大学 航空学院,西安710072)
(2.西安地平线电子科技有限公司,西安710072)
0 引 言
现代空战根据雷达探测范围和使用武器类型可分为超视距空战和近距空战。随着机载雷达和空空导弹性能的提升,空战在超视距阶段结束战斗的比例已从20世纪80年代的不足30%上升到21世纪初的超过50%[1]。因此,如何在有限的机动能力下,使用高效的逃逸机动策略提高战斗机对中距空空导弹的规避、逃逸能力,对于提高其空战生存力至关重要[2]。
飞机规避导弹问题是追逃对策的一种,导弹是追击者,根据导引律策略追击飞机;飞机是逃逸者,决策最优控制策略逃脱导弹的追击。传统的飞机规避导弹通常采用专家系统法[3-7]、微分对策法[8-10]、最优控制法[11-13]以及模型预测法[14-15]求解最优或次优逃逸机动。专家系统法极其依赖人类专家的先验知识,当导弹或飞机子系统变化时,人类专家需要分析新的子系统并再次给出新逃逸机动策略。微分对策、最优控制以及模型预测方法都依赖于明确完备的数学模型,需要对复杂的微分方程求解析或数值解。飞机规避导弹问题包括众多复杂非线性系统,各个子系统建模不免存在误差,这无疑加大了以上方法求解飞机规避导弹策略的难度。
近年来随着人工智能的发展,强化学习和深度神经网络相结合衍生出了一系列无需建模,只通过端到端学习,便能够实现从原始输入到输出的直接控制算法[16]。深度确定性策略梯度算法(Deep Deterministic Policy Gradient,简称DDPG)是其中一种可应用于连续动作空间的免模型算法[17]。国内外已经将该算法应用于不同的领域。WANG M等[18]利用DDPG算法研究了平面小车的追逃问题;S.YOU等[19]和R.Cimurs等[20]利用该算法研究了智能体在避开动态和静止障碍物的同时,追击目标的导航问题。上述研究中动态障碍物的动力学和运动学模型相对简单,相比于逃逸者,追击者并没有速度和机动性的绝对优势且追击者并未采用有效的追击策略。范鑫磊等[21]将DDPG算法应用于导弹规避决策训练,仿真验证了四种典型初始态势下逃逸策略的有效性,但在其研究中,空空导弹和规避飞机均采用简化模型,未考虑导弹导引律、飞机导弹气动模型以及飞机导弹相对运动模型,且其初始态势的范围相对较少,未与典型的逃逸策略进行对比,未能对DDPG算法学习到的逃逸策略有效性作出更精确的评价。
针对以上问题,本文基于DDPG算法,构建一套导弹规避训练系统。首先建立导弹飞机追逃模型,包括飞机导弹质点模型(考虑气动特性和推力特性)、空空导弹的导引律和杀伤率模型以及飞机导弹相对运动模型;再介绍DDPG算法并设计基于DDPG算法的导弹追逃问题奖励;然后将导弹追逃问题建模为基于DDPG算法的强化学习问题,构建基于DDPG算法的导弹规避训练系统;最后将基于DDPG算法的导弹规避训练系统自主学习到的逃逸机动策略与四种基于专家先验知识的经典逃逸机动进行对比,以验证基于DDPG算法的逃逸机动策略的有效性。
1 导弹飞机追逃模型
本文使用的导弹飞机追逃模型包括:飞机和导弹的质点模型、导弹的制导律模型、杀伤率模型以及导弹飞机相对运动模型等。
飞机规避导弹追逃模型的假设条件包括:(1)飞机和导弹都使用质点模型,考虑飞机和导弹的升阻特性和推力特性;(2)导弹采用比例导引制导律;(3)不考虑风的影响;(4)忽略侧滑角[9,22]。
1.1 飞机和导弹的质点模型
飞机和导弹的质点运动学模型为

式中:x,y,z分别为地轴系的三轴坐标,x轴指向正北,y轴指向正东,z轴竖直向下;V为飞行器飞行速度;˙为V在地轴系三个轴上的分量;γ为爬升角,表示速度和水平面夹角;χ为航迹方位角,表示飞行器飞行速度V在水平面的投影与x轴的夹角。
飞行器的质点动力学模型表示为[22]
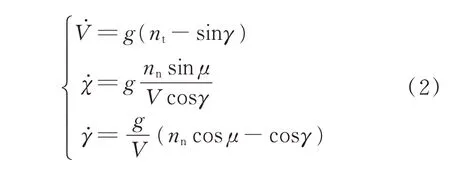
式中:˙分别为飞行器速度变化率、爬升角变化率以及航迹方位角变化率;nt,nn,μ为飞行器的控制量,其中nt为沿速度方向的切向过载,控制飞行器的加减速;nn为沿飞行器升力方向的法向过载,控制升力方向上的运动;μ为航迹倾斜角;g为重力加速度。

式中:L,分别为升力和阻力;T为发动机推力;m为飞机质量;α为飞行器迎角。
在导弹飞机追逃模型中,受飞机升力、阻力和推力的限制,飞机切向过载ntt∈[-2,1],法向过载nnt∈[-4,8],航迹倾斜角μt∈[-π,π]。(下标t,m分别表示飞机(目标)和导弹。)
1.2 导弹飞机相对运动模型
导弹飞机相对运动示意图如图1所示,[xm,ym,zm]T,[xt,yt,zt]T分别表示导弹和飞机在地轴系的位置矢量,D表示导弹相对飞机的位移,也称为瞄准线。

图1 导弹飞机相对运动模型Fig.1 Missile-aircraft engagement geometry model

导弹与飞机的距离:

Vm,Vt分别为导弹和飞机速度矢量,导弹相对飞机速度:

瞄准线变化率(导弹和飞机远离为正)为
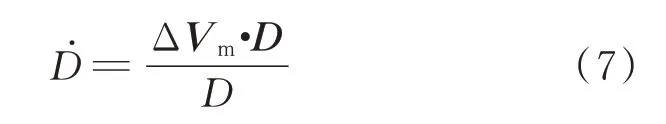
瞄准线角速度矢量:

瞄准线角速度大小:

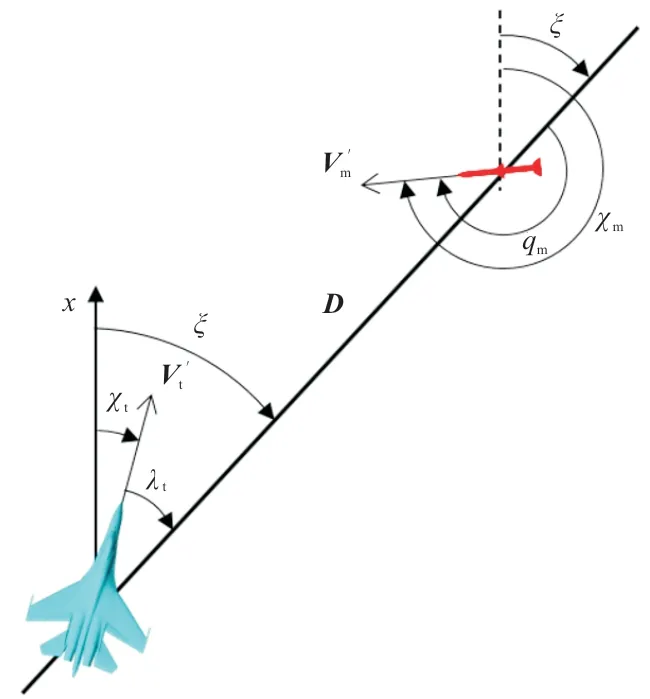
图2 飞机前置角和导弹进入角Fig.2 The aircraft bearing angle and the missile aspect angle
瞄准线方位角可表示为

水平面内飞机前置角(飞机速度与瞄准线之间的夹角):

式中:χt为飞机航迹方位角。
水平面内导弹进入角(导弹速度方向与瞄准线之间的夹角):

式中:χm为导弹航迹方位角。
1.3 导弹导引律与杀伤率模型
空空导弹采用比例导引律,比例系数为

式中:Vm为导弹飞行速度大小;C为常数。
当瞄准线距离小于导弹杀伤半径或小于1.5倍距离变化率与时间步长的乘积时,判定导弹命中飞机。

式中:kr为导弹杀伤半径;Δt为仿真时间步长;∨为数学符号“或”。
本文忽略导弹和飞机的探测传感器以及电子对抗模型,只从运动学和动力学的角度考虑导弹失效条件,当且仅当导弹远离目标(D˙>0)时,导弹失效。
2 DDPG算法
强化学习是智能体通过试错的机制和环境交互,目标是找到一个最优策略使得从环境中得到最大化的总奖励。强化学习可以被建模成一个马尔科夫过程(S,A,P,R),其中S表示状态集合,A表示动作集合,P表示状态迁移模型,R表示奖励函数。在时间步长t内,智能体处于st∈S状态,根据策略π采取动作at∈A,收到奖励rt。环境响应动作at,并向智能体呈现新的状态st+1∈S。时间步 长t的 总 奖 励 为其 中γ∈[0,1]为折扣率。智能体的目的是学习到一个能最大化期望奖励的策略[23]。
策略π下状态st采取动作at的期望动作值函数:

利用贝尔曼方程递归迭代更新估计动作值函数Q,直到找到最优策略。动作值函数使用贝尔曼方程估计[23]:

DDPG算法是一种不依赖模型的基于actorcritic架构的深度强化学习算法,由策略网络和动作值网络构成。其中,确定性策略μ(st|θμ)由参数为θμ的神经网络表示,动作值函数Q(st,at|θQ)由参数为θQ的神经网络表示[17,24]。
critic网络的输出标签由贝尔曼方程估计得到,用yt表示:

critic网络的损失:

critic网络根据式(18)使用反向传播方法,对参数θQ进行优化。
actor网络使用策略梯度优化,策略梯度指预期收益函数J对策略函数参数θμ的梯度[17]

式中:ρμ为确定性策略的状态分布。
D.Silver等[25]证 明 了 若 ∇θμμ(st|θμ)和∇a Q(st,at|θQ)存在,则确定性策略梯度∇θμJ存在。
DDPG借鉴深度Q网络(Deep Q Network)的经验池技术,把每一步的经验e=(st,at,rt,st+1)存储在经验池D={e1,e2,...em}中。由于在计算critic网络的损失函数时,yt依赖于Q网络,而Q网络同时也在训练,会造成训练过程不稳定。因此,在actor和critic中分别建立目标网络对当前动作进行估计。目标网络延迟更新,训练更稳定,收敛性更好。
3 奖励设计
不同于监督学习可以使用标签,强化学习必须通过尝试去发现采取何种策略才能获取最大的奖励,因此稀疏奖励问题是深度强化学习应用于实际的核心问题。稀疏奖励在强化学习任务中广泛存在。智能体只有在完成任务时,才能获得奖励,中间过程无法获得奖励[26]。
本文增加人为设计的“密集”奖励,也被称为成型奖励。在智能体完成任务的过程中,通过成型奖励引导飞机成功规避导弹。
3.1 成型奖励设计
在智能体未得到最终结果之前,成型奖励可以评价智能体的策略。因此成型奖励的设计要准确,否则将导致策略函数收敛到局部最优。越复杂的强化学习问题,影响奖励的因素越多,成型奖励设计的难度越大。
本文利用导弹飞机相对态势参数设计成型奖励(式(20)),引导飞机规避导弹,加快算法的收敛速度。

式中:D0为导弹与飞机初始距离;为瞄准线变化 率 绝 对 值 的 最 大 值;Ci,i=1,2,…,6分 别 为 各 分 项 奖励在总奖励中的权重系数;r d为导弹与飞机距离奖励,为导弹与飞机距离变化率奖励,(r d和描述了飞机导弹的距离态势);rλ为飞机前置角奖励,r q为导弹进入角奖励,(rλ和r q描述了飞机导弹的角度态势);r Ma为飞机飞行马赫数奖励,其目的是防止飞机失速;r h为飞机飞行高度奖励,其目的是防止飞机撞地。
本文方法对局部成组偏好的处理方式是刚性的,若采用柔性方式处理,则有2种可能的方案:①在DSM和耦合矩阵中的特定构件对之间分别增加权重值和相似度值,其缺点是容易导致算法的病态收敛问题[8];②将特定的模块化驱动因素、构件及其之间的映射关系从DPM/MIM中抽取出来单独放入新矩阵,并将新矩阵的聚类准则作为多目标优化算法的额外优化目标。该方案使得多目标优化问题变为高维多目标优化问题,其缺点是大大增加了算法计算负担,且优化质量下降。
3.2 稀疏奖励设计
稀疏奖励存在于绝大部分强化学习问题中,即任务完成后的奖励。飞机规避导弹问题的稀疏奖励是导弹飞机的交战结果,表示为
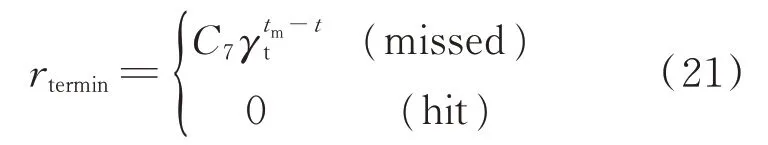
式中:γt∈[0,1]为折扣系数;tm为交战结果产生的时刻,即终局时刻;t∈[0,tm]为当前时刻;missed表示飞机规避成功;hit则表示导弹成功命中飞机;C7为成功规避奖励的权重系数。
结合式(20)~式(21),可得到总奖励表达式:

式(20)和(21)中各奖励权重系数Ci,i=1,2,…,7需要结合奖励参数的取值范围确定。
首先选取的是C7的值,因为根据式(21),规避成功奖励为C7·1,被击中或坠毁的奖励为0。本文选取C7=40,即成功逃逸后的奖励为40。根据C7=40综合考虑式(20)各个奖励的取值范围,Ci,i=1,2,…,6的值如表1所示。

表1 奖励系数值Table 1 The values of reward coefficients
4 基于DDPG的飞机规避导弹训练系统框架
把飞机规避导弹问题建模为一个强化学习问题,飞机与导弹在时刻t的运动参数和相对态势为强化学习的状态st,飞机t时刻的控制指令为强化学习的动作at,导弹飞机的追逃模型是强化学习的环境。
基于DDPG强化学习方法、导弹飞机追逃模型及飞机规避导弹的奖励设计,可建立飞机规避导弹训练系统,如图3所示。

图3 基于DDPG的飞机规避导弹训练系统Fig.3 The missile evasion training system based on the DDPG
基于DDPG的飞机规避导弹训练系统的状态st共8个,如表2所示。动作at共3个,如表3所示。
表2和表3中的状态st和动作at分别为actor网络的输入和输出。输入和输出的量都在-1到1之间,输入输出根据各自取值范围进行归一化和反归一化。

表2 飞机规避导弹训练系统的状态Table 2 T he states of the missile evasion training system

表3 飞机规避导弹训练系统的动作Table 3 The actions of the missile evasion training system
基于DDPG的智能体只依赖飞机规避导弹环境产生并存储在经验池中的经验数据和式(22)的奖励设计,在没有其他先验知识的情况下,通过训练找到行之有效的逃逸机动策略。
5 仿真过程与结果
5.1 初始场景设置
空空导弹攻击区是指空空导弹发射时刻能够命中目标的空间区域。导弹攻击区与许多因素有关,包括导弹和飞机的初始速度和高度、导弹离轴发射角、目标进入角、导弹制导律和目标机动方式等。它不仅是衡量空空导弹攻击能力的指标,也是衡量目标飞机逃逸机动策略有效性的指标。在其他影响因素相同的前提下,飞机逃逸机动对应的导弹攻击区越小表明飞机逃逸机动越有效。
考虑到超视距空战场景中,导弹迎面发射对目标飞机的威胁最大,因此本文将攻击区的范围限制在飞机前置角-30°~30°的范围内,本文使用如图4所示的攻击区作为逃逸机动策略的评价标准。

图4 飞机前置角-30°~30°攻击区Fig.4 The attack zone of aircraft bearing angle ranging from-30°to 30°
智能体训练的初始场景配置如下:飞机位置不变,始终在原点,航向正北。导弹初始位置在以飞机为圆心,半径20~40 km,飞机前置角-30°~30°的闭合范围内(图4闭合线部分),导弹的航向始终指向飞机。考虑导弹从载机发射,导弹初始高度和马赫数取决于载机的高度和马赫数。因此本文设置飞机导弹的初始高度都为8 000 m,初始马赫数都为0.9。导弹发射后会急剧加速,导弹马赫数随飞行时间变化如图5所示,最大马赫数大于5.0。

图5 导弹飞行马赫数随时间变化Fig.5 The missile Mach number changes with time
5.2 训练过程与结果
总共训练约70万次,仿真共生成2.3亿组经验(e=(st,at,rt,st+1))数据。
训练过程与结果如图6所示,x形符号表示飞机以非正常飞行状态(失速或撞地)结束仿真,圆形符号表示飞机被导弹击中,三角符号表示飞机成功规避导弹。

图6 训练过程与结果Fig.6 Training process and results
从图6(a)可以看出:在前1 000代训练中,飞机失速或撞地占52.6%,被导弹击中占47.3%,飞机只成功规避一次导弹。此时智能体尚未学会控制飞机正常飞行,更无法规避导弹。
第2 000代~3 000代的训练结果如图6(b)所示,可以看出:飞机失速或撞地占15.5%,被导弹击中次数占70.9%,飞机成功规避导弹占13.6%。此时智能体已能逐渐控制飞机飞行,然而还未能有效规避导弹。
最后1 000代的训练结果如图6(c)所示,可以看出:飞机失速或撞地只占总数的2.7%,被导弹击中占37.0%,飞机成功规避导弹占总数的60.3%。此时智能体已自主学习到一种飞机规避导弹策略,能在约25 km外规避导弹。
智能体学习到的逃逸机动策略如图7所示,实线为飞机,虚线为导弹。图7(a)是逃逸机动的三维轨迹图,图7(b)和图7(c)是以地轴系x坐标为横坐标,地轴系y坐标和高度h分别为纵坐标的飞机导弹飞行轨迹图。三角形表示起点,实心圆表示终点。图7(b)中y轴正方向向下。

图7 基于DDPG算法的逃逸机动策略Fig.7 The evasive maneuver strategy based on the DDPG algorithm
从图7可以看出:智能体实现的逃逸机动策略为导弹发射后,飞机急剧转弯,尽快把导弹置于尾后,转弯的同时降低高度直至5 000 m左右,最后拉起飞机成功规避导弹。
5.3 典型逃逸机动策略介绍
参考文献[4-5,7,27]对飞机规避导弹问题的研究,总结出四种典型的依赖导弹规避先验知识的逃逸机动策略。
(1)定直平飞:逃逸飞机保持初始高度、速度和航向飞行。
(2)蛇形机动:逃逸飞机航迹方位角χ在一定幅值范围内连续周期性变化。
(3)水平置尾机动:逃逸飞机以最大稳定盘旋角速度转弯至置尾(飞机与导弹航向偏差小于5°),然后以加力状态平飞逃逸。
(4)置尾下降机动:逃逸飞机以大于90°滚转角边转弯边下降直至飞机与导弹航向偏差小于5°,后改出下降在低空以加力状态平飞逃逸。
典型逃逸机动策略如图8所示。
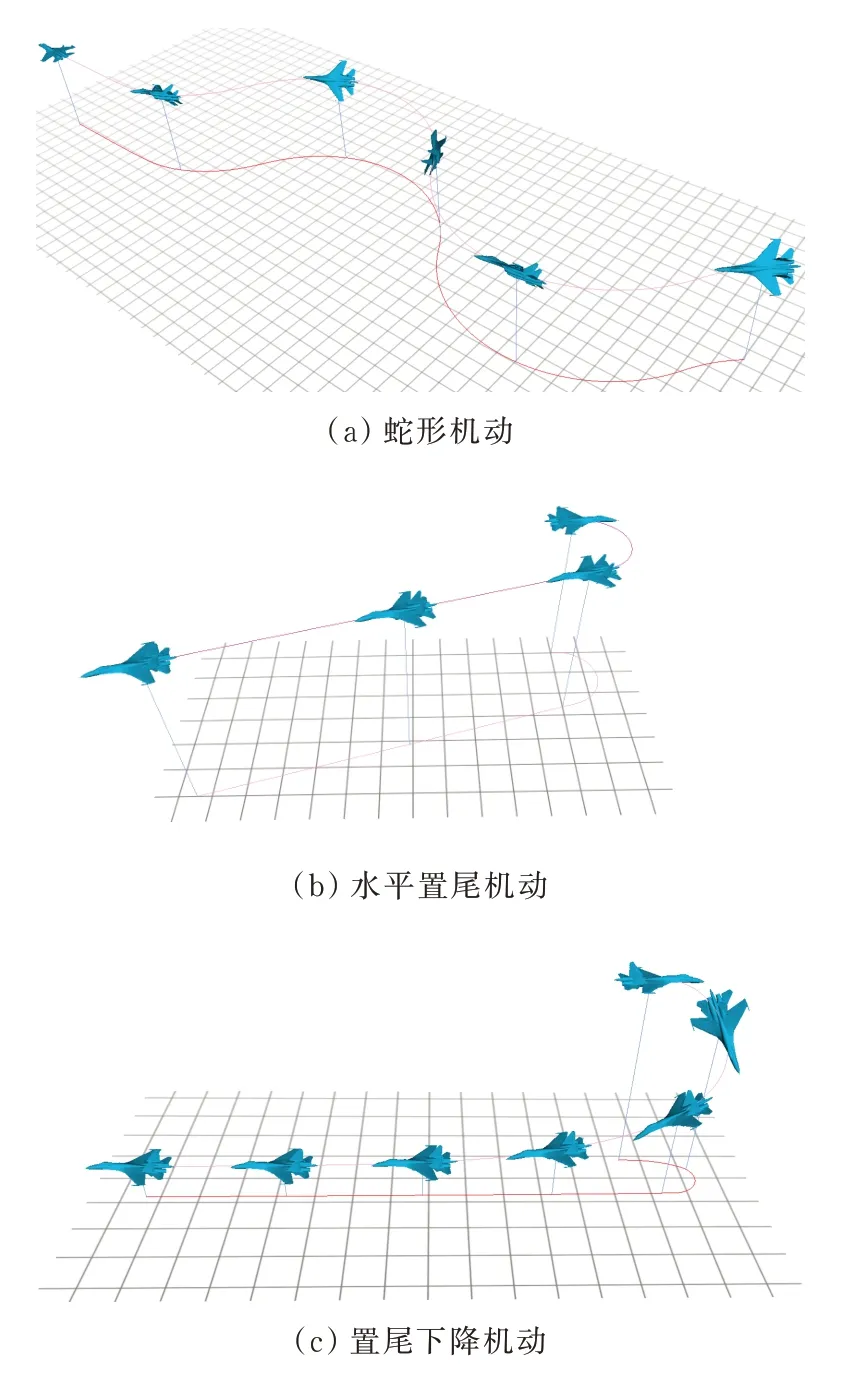
图8 典型逃逸机动策略Fig.8 The classic evasive maneuver strategies
与智能体训练导弹规避的初始条件相同,各个典型逃逸机动的攻击区,如图9所示。

图9 典型机动策略下的攻击区Fig.9 The attack zones of classic maneuver strategies
结合图6(c)和图9得到典型机动策略和智能体自主学习的逃逸机动策略的攻击区对比图,如图10所示。

图10 所有逃逸机动策略攻击区对比图Fig.10 The attack zones of all evasive maneuver strategies
从图10可以看出:所有逃逸机动策略的攻击区从大到小依次为:平飞机动>蛇形机动>水平置尾机动≈智能体实现的逃逸机动>置尾下降机动。
综上所述,利用深度确定性策略算法实现的逃逸机动,在没有任何飞机规避导弹先验知识的情况下,攻击区优于蛇形机动,与水平置尾机动持平,稍劣于置尾下降机动。
6 结 论
(1)本文所构建的基于DDPG算法的导弹规避训练系统表明,智能体在不依赖导弹规避先验知识、仅凭借仿真数据和奖励的情况下,最终能够自主学习到一种有效的逃逸机动策略。
(2)通过与四种典型逃逸机动策略的攻击区相比,智能体逃逸机动攻击区仅次于置尾下降攻击区,但智能体实现的逃逸机动策略对导弹规避的先验知识需求最少。
