超声激励下的裂纹区域温度缺陷信号特征分析

刘海龙，郑 飞，吴海波

(1.湖南铁道职业技术学院轨道交通智能控制学院，湖南 株洲 412001；2.上海交通大学机械与动力工程学院，上海 200240)

1 引言

挖掘机等重型装备和装甲装备在长期工作在恶劣严苛的环境作业期间，某些部位经受着交变应力的作用，使得某些关键部位易发生疲劳和磨损等损伤，在其表面或亚表面产生裂纹和分层等缺陷。若不能在缺陷产生初期进行有效的检测并及时修复，缺陷问题会进一步加重从而形成宏观裂纹并突然发生断裂等危险，这将极大的影响到装备安全和人员安全，轻者造成装备性能失效，既定无法顺利完成作业任务，重者造成人身伤亡。为避免此类事故造成的经济损失及人员安全隐患，有必要定期对关键部件进行缺陷检测。

超声红外热像技术[1-4]是一种以超声脉冲为激励源的红外热像技术，它通过激发接触面相对运动摩擦生热，利用红外热像仪捕捉被测对象表面温度信息，对疲劳裂纹等闭合类缺陷有突出检测效果，非常适合装备中的平板、轴、箱体等零部件的裂纹检测，其基本构成示意图，如图1所示。

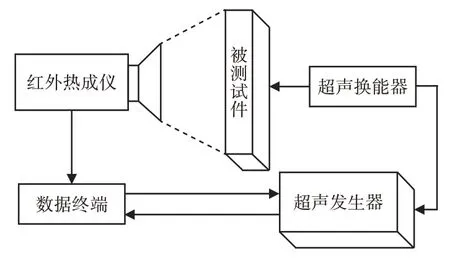
图1 超声红外系统的构成示意图Fig.1 Schematic Diagram of Ultrasonic Infrared System

超声脉冲作用时间短，不受复杂结构的影响，可实现装备结构件的原位检测。因此，超声红外热像技术非常适用于装备中结构件的疲劳裂纹检测[5-7]。将以金属平板试件为研究对象，探索分析裂纹区域温度的空间与时间分布规律，进而总结出裂纹区域温度缺陷信号的判断标准，为今后超声红外热图像增强和缺陷特征信息的提取以及超声红外热像技术在挖掘机等重型装备和装甲装备的裂纹检测应用提供技术支撑。

2 裂纹区域热传导模型分析

2.1 热传导理论分析

依靠物体内部微观粒子的热运动而产生的热量传递过程称为导热[8-9]。温度差异是热传导的驱动力，且热传导仅发生在物体内部：温度永远由较高的部分传导到温度较低的部位，热传导的最终形式为各部分温度趋于一致。当物体各部位的温度不相等时，热量由高温区域“流向”低温区域。

在材质均匀、各向同性的介质中，热传导遵循傅里叶定律的向量，如式(1)所示。

式中：n—法向单位向量；∂T∂n—温度在n方向上的导数；λ—导热系数；q—热流密度。公式表明，热流密度仅与同一方向上的温度变化率有关。

热量扩散快慢与热扩散系数紧密相关，热扩散系数α表征整个区域内温度趋于一致的能力，模型如式(2)所示。

式中：ρ—密度；C—比热容。

2.2 热传导模型分析

超声激励试件时，缺陷区域由于材质不均匀或裂纹的闭合面摩擦等因素产生热量，而其他无缺陷区域不生热，温度的变化使得热量由缺陷部位向四周扩散，在红外图像序列中就表现为亮斑面积随时间的推移逐步增大。以平板试件贯穿裂纹为研究对象，对激励过程中的裂纹生热及热传导进行仿真，计算其表面温度场分布及变化。

厚度为D的平板试件，其上边缘存在一个长为L的裂纹，已知导热率为λ，密度为ρ，比热容为C，生热功率为，该试样有均匀的初始温度T0，与外界绝热，试样热参数各向同性且不随温度与激励时间变化。

热传导过程通常为(1～2)s，可将x轴视为无限大，y轴视为半无限大，如图2所示。其数学模型，如式(3)所示。

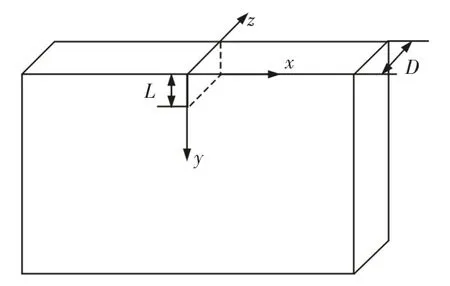
图2 平板试件贯穿裂纹示意图Fig.2 Schematic Diagram of Plate Event Penetration Crack

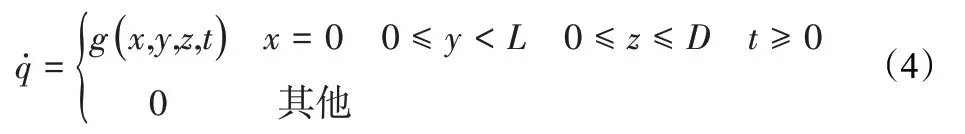
对于贯穿裂纹而言，忽略热量、温度分布沿试样厚度方向的变化，即∂T∂z=0，上述3D半无限大对象的传热问题简化为如图3所示的2D半无限大对象传热问题，其数学模型，如式(5)所示。

图3 简化后的模型Fig.3 Reduced Mode

该模型对应的2D无限大对象传热问题的数学模型，如式(7)所示。

求得2D无限大对象传热问题的Green函数表达式，如式(9)所示。

采用镜像法求解2D半无限大对象传热问题的Green函数表达式，如式(10)所示。

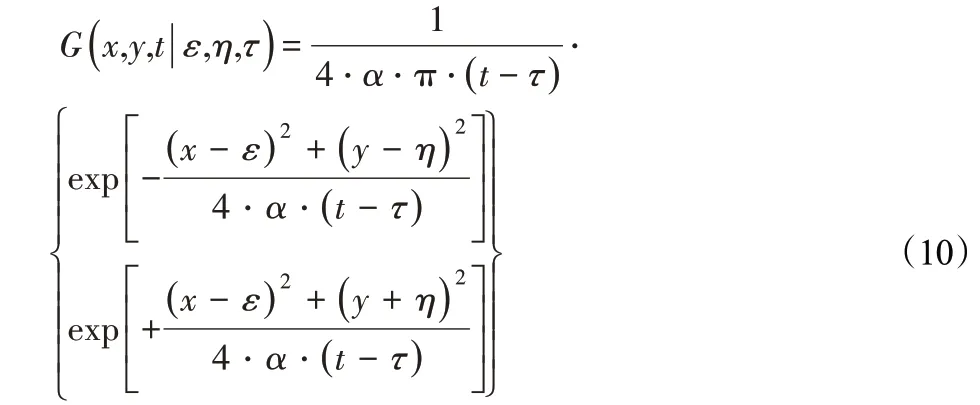
则2D传热问题的解可由Green函数，如式(11)所示。

结合初始条件和边界条件，式(11)可表示为，如式(12)所示。

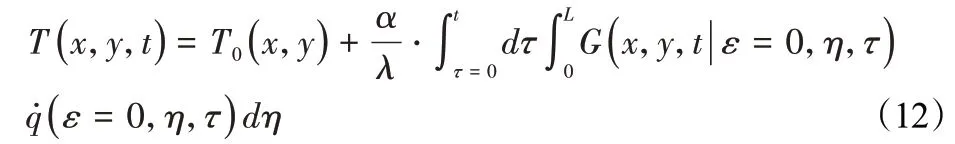
则变化的温度场可表示为，如式(13)所示。

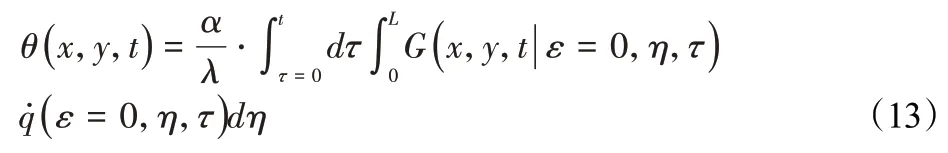
3 裂纹区域温度空间分布规律分析

3.1 裂纹区域温度空间分布仿真分析

根据裂纹区热传导模型，在MATLAB环境下对铝合金平板贯穿裂纹在超声激励下的生热及热扩散过程进行仿真研究[10-11]，平板试件的裂纹位于平板一侧长边中间位置，平板主要性能参数，如表1所示。并设置采集频率为30Hz，激励时间为1s。第10、20、30帧的图像温度分布情况，如图4所示。取与线热源铅垂线的位置，以裂纹为中心选择附近20个点，绘制出的第10、20、30帧仿真温度值随像素变化曲线，如图5所示。

表1 平板试件主要性能参数Tab.1 Main Performance Parameters of the Flat Specimen

图4 仿真温度分布图Fig.4 Simulation Temperature Profile

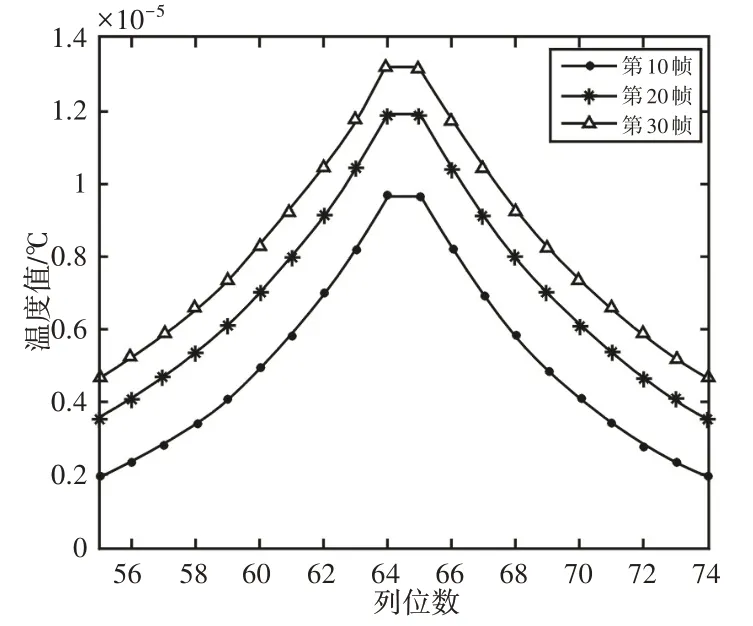
图5 仿真温度值随像素变化曲线Fig.5 Curve of Simulation Temperature Changes with Pixels

由图4可知，随着时间的增加，裂纹位置温度升高，周边区域由于热扩散以亮区的形式显示出来并逐渐增大。从图5中可以看出，水平方向上温度峰值出现在裂纹处，热量由裂纹向两侧均匀扩散，随时间推移裂纹中心温度越来越高，总体温度值也逐步升高。

3.2 裂纹区域温度空间分布实验分析

为验证仿真分析有效性，开展了平板超声红外实验，以获取不同时刻的红外热图像，研究裂纹区域的温度空间分布特点。实验选用的材料为铝合金平板，为利于裂纹产生，对铝合金平板打磨处理，材料打磨后的表面均很光滑，表面辐射率低，且容易造成反射影响红外图像，并在试件表面喷涂一层厚度适当的涂料可以大幅度提高辐射率，有效改善热像质量，提高检测效率，降低误检率。实验测试时，在以双层紧致布料为屏蔽工具搭建的红外暗室内，以超声作为激励源，利用FLIR T640型红外热像仪对板件进行红外热像检测。

为有效对比仿真分析，选择的激励后第10、20、30帧减背景后的图像作为实验温度分析对象，如图6所示。参照仿真数据与实测数据两者实际距离上的比例，为分析实际中裂纹垂直方向上温度的分布情况，选择热像图中以裂纹为中心且垂直于裂纹的水平线上左右各50个像素点的温度值，绘制的实验图像温度值随像素变化曲线，如图7所示。

图6 实验温度分布图Fig.6 Experimental Temperature Profile

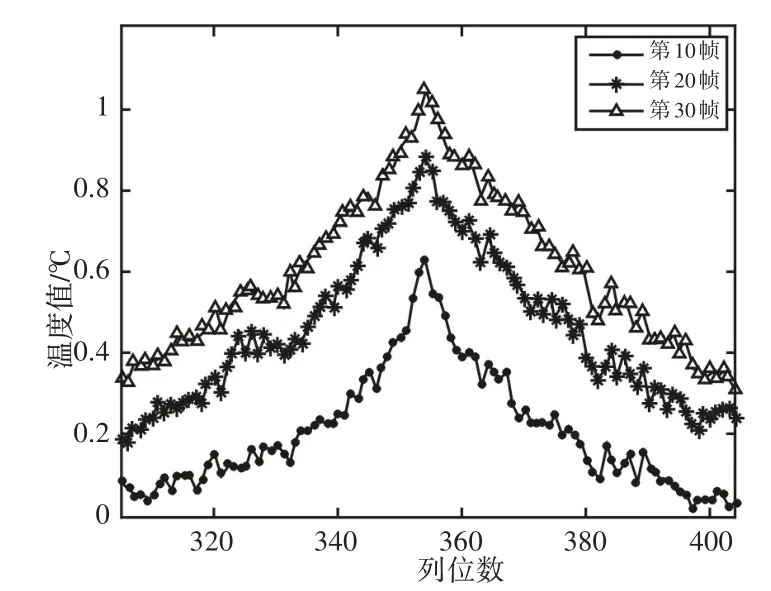
图7 实验温度值随像素变化曲线Fig.7 Curve of Experimental Temperature Changes with Pixels

由图6可知，随着时间推移，裂纹位置亮度逐步增加，发亮区域面积逐步增大，表明温度逐渐升高，热量逐渐向四周扩散。对比图4与图6、图5与图7可知，随着超声激励的持续，裂纹摩擦产生的热量使得裂纹位置的温度值逐步增大，生成的热量以裂纹为中心逐渐向四周扩散，平板上裂纹附近的温度空间分布曲线呈现出良好的一致性，验证了仿真分析的正确性。

4 裂纹区域温度随时间变化规律

4.1 裂纹区域温度随时间变化仿真分析

4.1.1 温度峰值随时间的变化特点

由裂纹区域温度空间分布分析可知，温度峰值出现在裂纹顶端位置，并遵循式(13)的变化规律，超声持续激励下温度峰值随激励时间的变化关系，如图8所示。

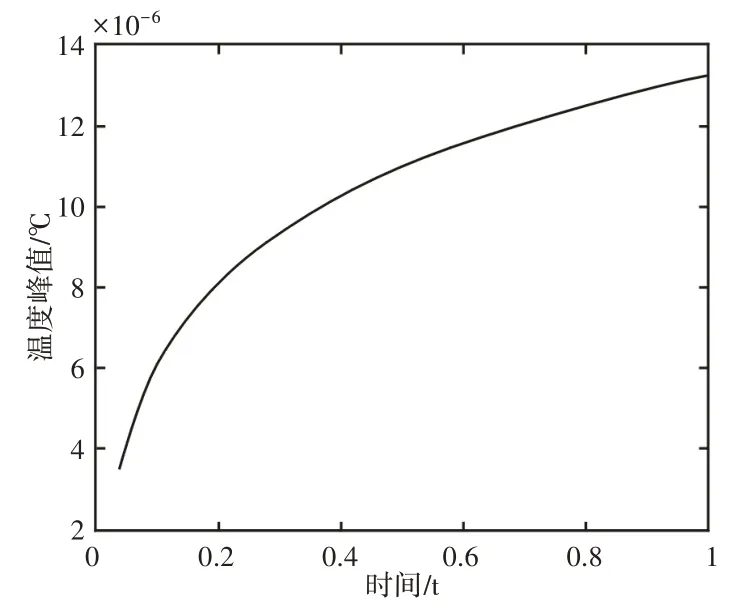
图8 温度峰值-激励时间变化曲线Fig.8 Peak Temperature-Excitation Time Curve

激励阶段温度峰值的变化规律为：随着超声的持续激励，温度峰值逐渐增加，但温度梯度逐渐减小，如图8所示。

4.1.2 温度均值随时间的变化特点

设定超声激励的时间为τ0，试样从线热源吸收的热量Q(τ)为：

由于裂纹面等效为恒定的线热源，因此在(0～τ0)的时间里，热量值随时间呈线性增长，时间超过τ0后，热量值保持不变。

在试件厚度较小的情况下，试件温度不随厚度变化，裂纹区域表面温度之和能够表征整个裂纹区域体积温度之和。由公式Q=C·ρ·V·Δt可知，同一试件比热容C、密度ρ和体积V完全相同，热量与温度成正比，可以利用温度之和表征热量之和。由于不同区域的总温度值差别较大，不便于比较，而温度均值与总温度值趋势相一致，故采用温度均值的变化表征热量的变化。当选定整个平板时，激励阶段平板的温度均值变化曲线，如图9所示。

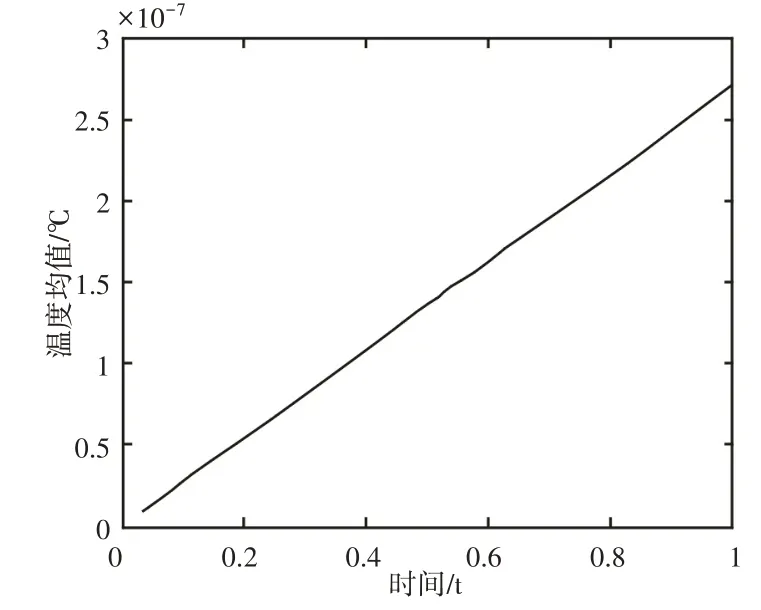
图9 温度均值-激励时间变化曲线Fig.9 Temperature Mean-Excitation Time Curve

温度均值在超声激励阶段随时间呈线性关系，即随着时间的后移，温度均值在直线上升，如图9所示。

4.1.3 区域面积对温度峰值及温度均值的影响

前面对温度峰值与温度均值的分析都是基于整个平板试件的，而在实际检测中，干扰因素多，检测工作人员一般会在图像序列中截取部分区域分析其温度峰值与均值随时间的变化情况。下面分析选取不同区域面积情况下，区域内温度峰值与均值的变化情况。

温度峰值通常出现在裂纹顶端位置，当选取区域将整个裂纹包含在内时，温度峰值的变化不受区域的影响，与图8中的曲线完全相同。由于在超声激励下裂纹区域的生热功率不变，故单位时间内生热量不变。温度均值由整个区域温度值的总和与该区域的面积大小相除得到，面积越大，热量越分散，温度均值就较小。

以裂纹为中心选择面积不同的五个区域，分析这五个区域内温度均值随时间的变化特点，不同区域温度均值-时间变化曲线，如图10所示。图中的五条曲线从上到下代表的面积逐渐增大。由图10可知，随着选取区域的增大，温度均值的变化曲线越来越接近于线性增长；从数值上来看，均处于温度峰值曲线与整个平板温度均值曲线之间。

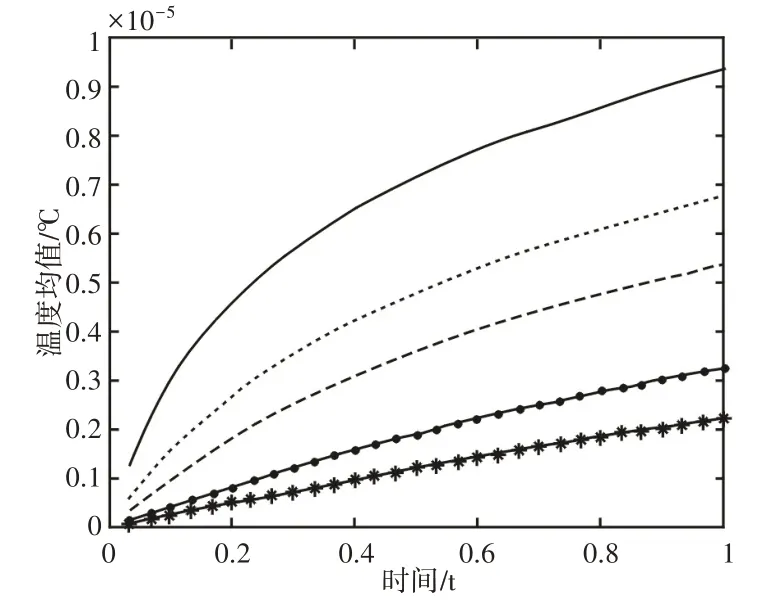
图10 不同区域温度均值-时间变化曲线Fig.10 Temperature Mean-Time Curve in Different Regions

因此，裂纹区域温度缺陷信号的判断标准可归纳为：超声激励过程中，裂纹区域温度峰值与均值的变化均为单调增加，且温度梯度逐渐减小；温度峰值的变化与选取区域无关，选定区域内温度均值的大小随选取区域面积的增大逐渐减小，变化曲线随选取区域面积的增大越来越接近于线性增长。

4.2 裂纹区域温度随时间变化实验分析

图11 减背景后的一帧图像热像图Fig.11 A Thermal Image of a Frame after Subtracting the Background

为验证缺陷信号判断标准的正确性，以平板裂纹检测数据为例对选定区域的大小对该范围内温度峰值与均值变化特点的影响进行实验分析。减背景后的一帧图像热像图，如图11所示。选取将裂纹缺陷包含在内的三个矩形区域，分别绘制的温度峰值和温度均值随时间的变化曲线，如图12、图13所示。

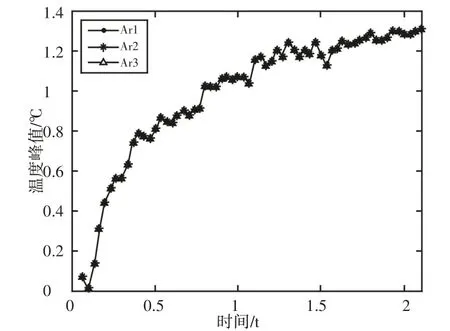
图12 温度峰值-时间变化曲线Fig.12 Peak Temperature-Time Curve

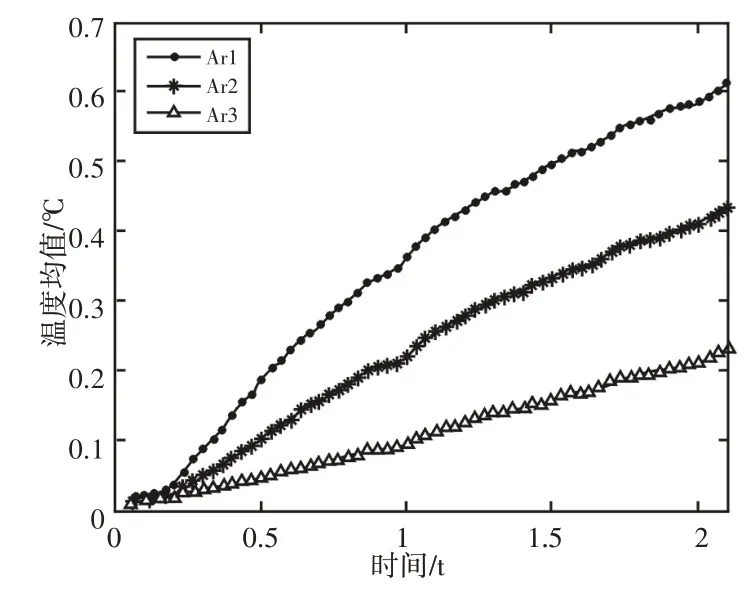
图13 温度均值-时间变化曲线Fig.13 Temperature Mean-Time Curve

平板试件位于整个图像的下半部分，试件上边缘中间位置存在裂纹，超声激励后裂纹生热，在红外图像中以亮区的形式表现出来，并随着热量扩散亮斑逐渐增大，如图11所示。温度峰值的大小与选取区域的面积大小无关，如图12所示。由于热量是由裂纹闭合面摩擦产生的，温度峰值必定出现在裂纹临近区域。只要把裂纹包含在所选区域中，峰值大小就与选取的区域大小无关。温度均值在超声激励阶段逐渐上升，且先呈线性上升，后呈斜率逐渐减小的上升，三条曲线由上至下所代表的区域为由小到大，面积越大，越接近于线性增长，如图13所示。实验分析与仿真分析结果相一致，验证了裂纹区域温度缺陷信号判断标准的有效性。

5 结论

以金属平板试件为研究对象，利用理论建模、仿真分析和实验测试等方法对超声激励下裂纹区域温度空间分布规律和温度随时间变化规律进行了分析研究，分析得到裂纹区域温度缺陷信号判断标准：超声激励过程中，缺陷区域温度峰值与均值的变化均为单调增加，且温度梯度逐渐减小；温度峰值的变化与选取区域无关，选定区域内温度均值的大小随选取区域面积的增大逐渐减小，变化曲线随选取区域面积的增大越来越接近于线性增长。