Floquet bands and photon-induced topological edge states of graphene nanoribbons∗

Weijie Wang(王威杰), Xiaolong L¨u(吕小龙), and Hang Xie(谢航)

College of Physics,Chongqing University,Chongqing,China

Keywords: Floquet bands,graphene,topological phase transition,edge states

1. Introduction

In recent years, the periodically-driven systems have attracted a lot of research concerns. By using the Floquet theorem to these systems,the time-dependent system can be transformed into the steady system with the infinite-dimensional Floquet Hamiltonian. This Hamiltonian generates a serial of quasienergies due to Floquet band branches in the energy domain.[1]

Under the light radiation,graphene-like 2D materials can obtain some topological properties,such as the photo-induced Hall effect,as well as some photo-induced energy gaps.[2]Recently, this type of Hall effect has also been experimentally observed.[3]In addition,the graphene system under illumination may exhibit edge current and magnetic field.[4]Moreover,it is experimentally and theoretically confirmed that radiated graphene has the quantum-rachet effect,which causes the unidirectional current.[5]According to the Floquet theorem, under the periodic perturbations of external fields,both graphene and the Su–Schrieffer–Heeger systems can generate unidirectional currents and various topological phases.[6,7]Besides,the light resonance may cause some suppression effect of ballistic conduction in graphene systems.[8]

In the aspect of topological properties,researchers found that radiated graphene nanoribbons (GNR) have the dynamic gaps, in which there exist some topological chiral edge states.[9]These edge states have a bulk–edge correspondence with the topological characteristics of its bulk system.[10,11]More recently, in the Floquet researches, some high-Chernnumber systems are discovered in the systems with the complex periodic perturbations (such as quenching systems).[12]Under the high-frequency approximation, one can derive the effective Hamiltonian with one or more perturbation terms(by the Brillouin–Wigner theory)in the hexagonal lattice of twodimensional materials.[13,14]Besides, some experimental observations have also revealed the Floquet–Bloch states and the interaction with the dressed Volkov states in the topological insulator with the Dirac fermions, which established a systematic path for the coherent manipulation of solids via lightmatter interaction.[15,16]

However,many of the current works on the topology analysis and quantum transport of radiated two-dimensional materials are based on the high-frequency approximation.[13,17–21]In the realistic graphene systems,due to the large hopping energy of 2D materials (from 1 eV to 3 eV), the corresponding high-frequency light(with the energy about above 10 eV)goes into the ultraviolet range. This is experimentally unrealistic and can result in the photon-ionization of the samples.Therefore,the low-frequency illumination is more suitable for experimental researches of Floquet electronic systems. We notice that some recent theoretical work considers the lowfrequency systems, such as the effective Hamiltonian model reported by Voglet al.[22]and the topological phase transition studies of black phosphorene by Kanget al.[23]Besides,Usajet al.[9]and Torreset al.[24]considered the frequencies smaller than the bandwidth of the Floquet topological insulator, and analyzed the edge states and the transport properties.Perez-Piskunowet al.[25]found the hierarchy of Floquet gaps and topological phase transitions in the driven honeycomb lattices with the very low driven frequencies. But the detailed investigations of the topological properties of the graphene system,as well as the edge state distributions and its relation with the photon excitations at low (or arbitrary) frequencies, still remain unexplored.

In this paper,we use the non-perturbative Floquet Hamiltonian and Berry curvature formula to study the Chern numbers at arbitrary frequency.We find that there exist many types of photo-induced edge states and high-Chern-number states in the low frequency range,besides the ordinary quantum anomalous Hall(QAH)states with the Chern number of±1 under the high-frequency illumination. All these edge states have topological properties and follow the bulk–edge correspondence.We also find the correspondence of the Floquet bands and the edge states distributions in the decomposed photon-number space.Moreover,we investigate the size effect in zigzag GNR.

This paper is organized as follows. Section 2 gives the theoretical introduction of this work, including the theory of the Floquet band for graphene systems and the Chern numbers calculation method. Section 3 shows our results and discussion, including the topological phase transitions of GNR, the band structures, the edge state profiles in the photo-number space,and the size/photo-number effects. Section 4 gives the conclusions of this work.

2. Theories and methods

2.1. Floquet–Bloch Hamiltonian for the honeycomb lattice systems

In this work, we use the tight-binding model for the graphene system with the nearest neighbor approximation

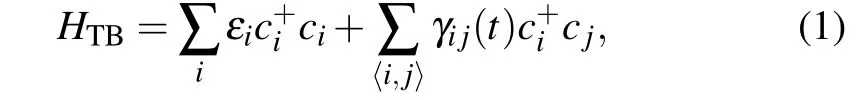
wherec+iandciare the electron creation and annihilation operators at sitei,εiis the on-site energy,andγi j(t)is the timedependent hopping energy between sitesiandj;〈i,j〉means the hopping only occurs between the nearest neighbors.

We consider a beam of circularly-polarized light vertically radiated on the graphene plane. The photon–electron interaction is considered by modifying the hopping parameters with the Peierls substitution[25]

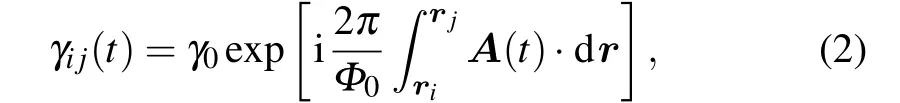
whereΦ0=h/eis the quantum flux with the Planck constanthand elementary chargee;γ0is the hopping energy between sitesiandjwithout radiation,riandrjare the positions of the two sites; andA(t)is the vector potential of the light. In the case of the circular polarization with angular frequencyωand amplitudeA0,A(t)=A0(cosωt,sinωt);the corresponding electric field is given asE(t)=E0(−sinωt,cosωt)withE0=A0ω.

Since the Hamiltonian of the light-driven system is periodic in time domain with the periodT,H(t)=H(t+T)andT=2π/ω,we may use the Fourier transformation to change the time-dependent Hamiltonian into the frequency domain according to the Floquet theory[1]

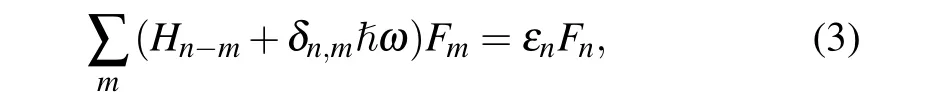
whereεnis the quasienergy;HnandFnare the Fourier component of the Hamiltonian and the wave function, respectively.The former component is calculated as

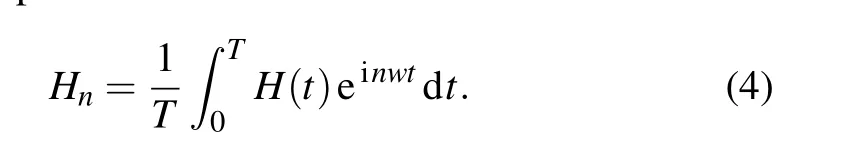
We can also write the whole HamiltonianHFin the extended Floquet–Hilbert(Sambe)space as[13]

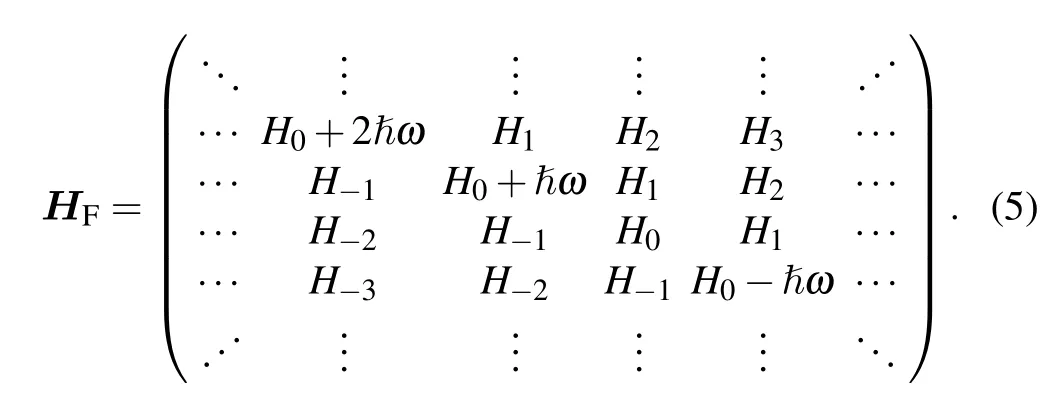
In practical calculations, people use the photon-number cut-off scheme to change the above infinite-dimensional Floquet matrix into some small Floquet matrix, which only includes finite Fourier components of the Hamiltonian. For example, the following Floquet Hamiltonian is cut off by one photon number(NF=1):

Figure 1 shows the lattice of the bulk graphene. With the tight-binding approximation and the Bloch theorem, we may obtain the Hamiltonian in the momentum space

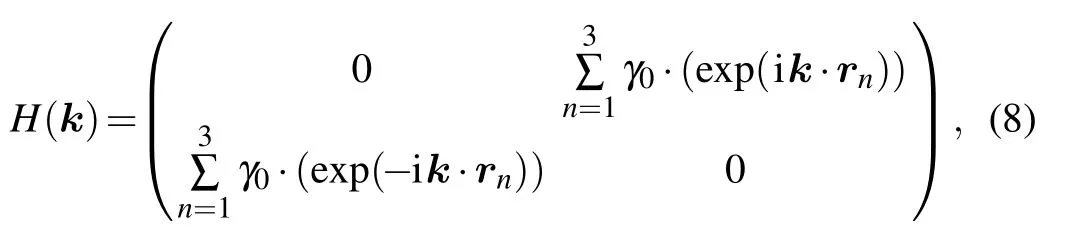
wherekis the Bloch wavevector in two dimensions, andγ0is the hopping energy between the nearest neighboring sites.When we consider the light radiation, the Peierls substitution(Eq. (2)) is employed. The Fourier component of the timedependent Hamiltonian is calculated as

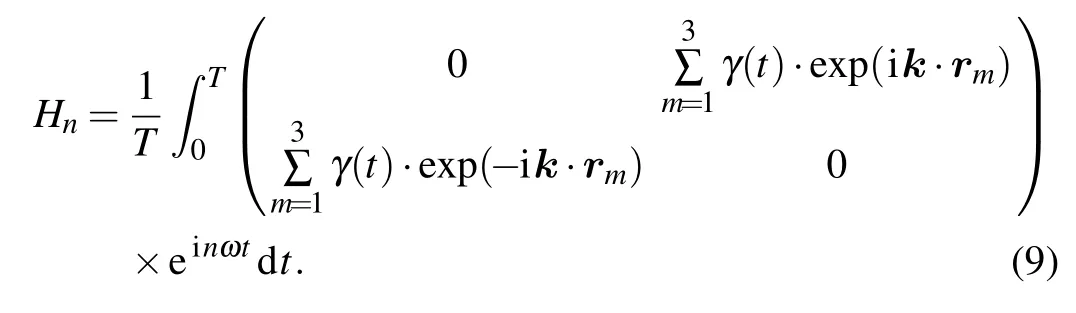
In our case, the vector potential is approximately spatial uniform in the region of the nearest neighboring atom sites(landl＇)of graphene. So the hopping energy under radiation can be written as

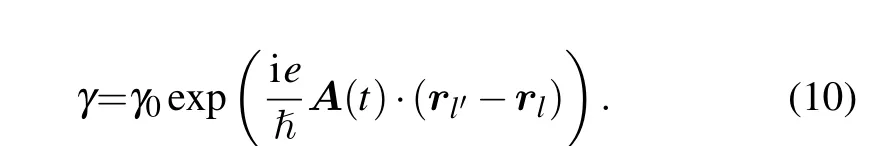
The vector potential of the circularly polarized light is given asA=A0(cosωt·x+sinωt·y); and the displacement between two neighboring atoms isrl＇l=rl＇−rl=a(cosαl＇l·x+sinαl＇l·y), whereαl＇lis the angle betweenrl＇landxaxis. Substituting these expressions into Eq.(10),we obtain

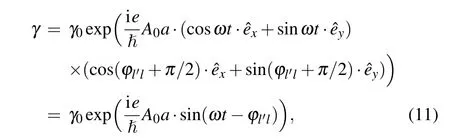
whereϕl＇l=αl＇l −π/2 is the angle betweenrl＇landy-axis(see Fig.1,ϕl＇lforr1,r2,andr3are 0,θ,and−θ,respectively).Then by applying the Jacobi–Anger expansion

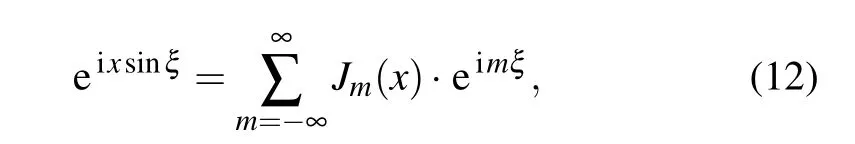
whereJm(x)is them-th order Bessel function, Eq.(9)can be rewritten as

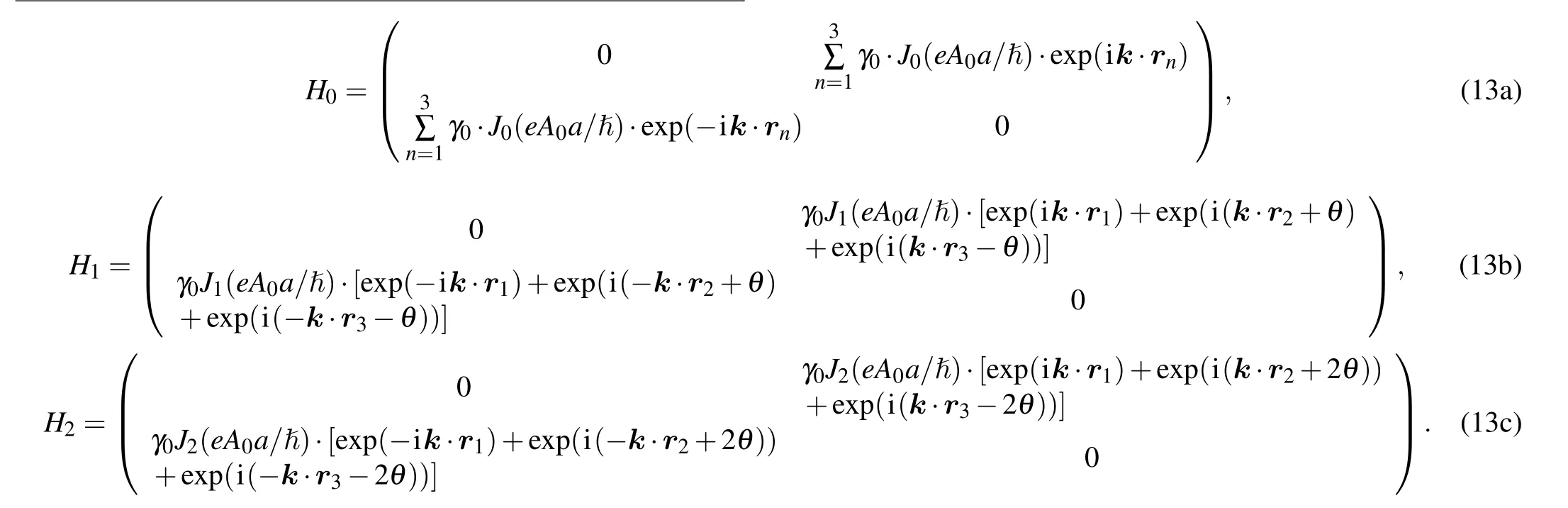
Similarly,H−1andH−2expressions can also be derived by this way.

For the GNR system under the light radiation,we also use the Peierls substitution to Eq.(1)and use the Floquet theorem to obtain the Floquet Hamiltonian.

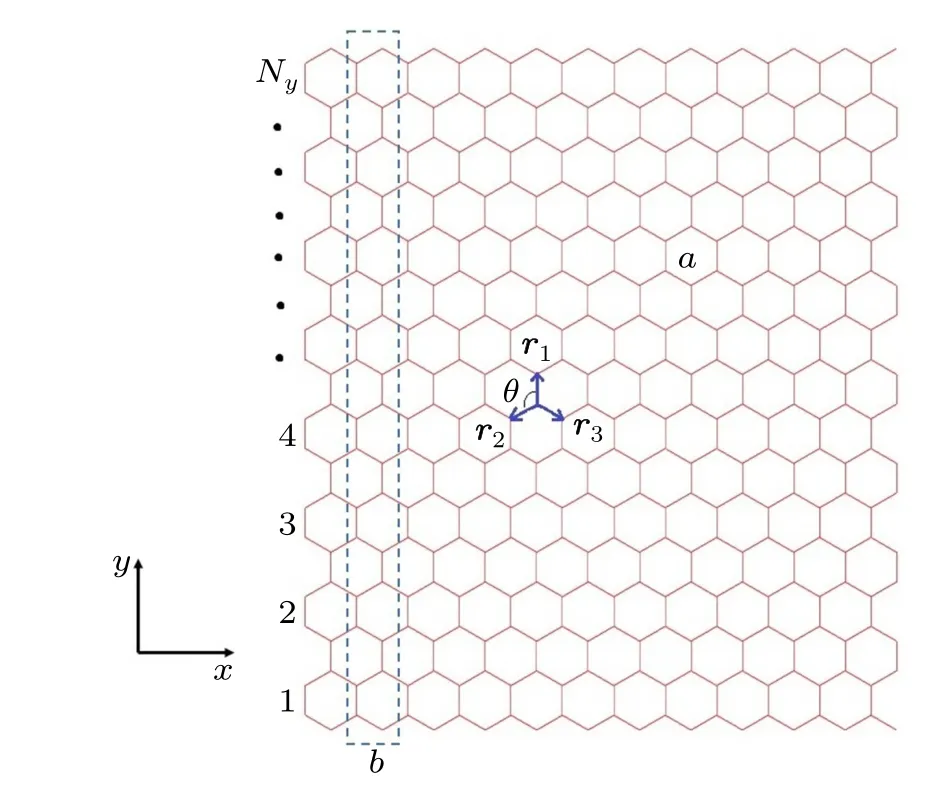
Fig.1. Honeycomb lattice of graphene and GNR in the real space. The bond length is a and the dashed rectangle box denotes the unit cell of GNR(with the period b and Ny repeat units in y direction),r1,r2,and r3 are the three vectors between the nearest-neighboring sites.

2.2. The Berry curvature and Chern number calculations

When the Hamiltonian in the momentum space is obtained, we can calculate the Chern number, which can characterize the topological property of the Floquet system. The Chern number of then-th band is defined by an integral in the first Brillouin zone(FBZ)

In this paper, we use a more efficient numerical method to calculate the Berry curvature and the Chern number.[26]Firstly,we define the following normalized link quantities:

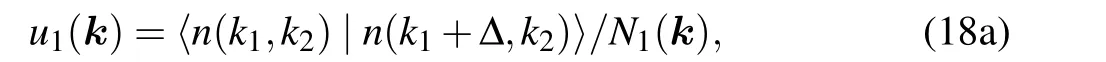
where ∆ is the infinitesimal shift inxorydirection;N1(k),N2(k),N12(k), andN21(k) are the corresponding normalization constants, for exampleN1(k) =|〈n(k1,k2)|n(k1+∆,k2)〉|. The Chern number can be evaluated as the Berry curvature summation in the discretized FBZ

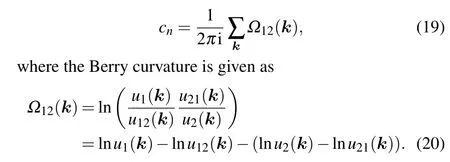
Here we give an equivalence proof between this new formula and the original Berry curvature definition (Eq. (15)).With the Taylor expansion and ignoring the higher order, we haven(k1+∆,k2)≈n(k1,k2)+∂k1n(k1,k2)·∆. Substituting this into Eq.(18a),we have

Then with the Taylor expansion of logarithm function ln(1+x)≈xand Eq.(16),we obtain

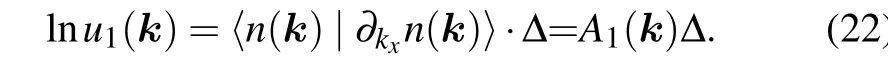
Similarly,we can prove that

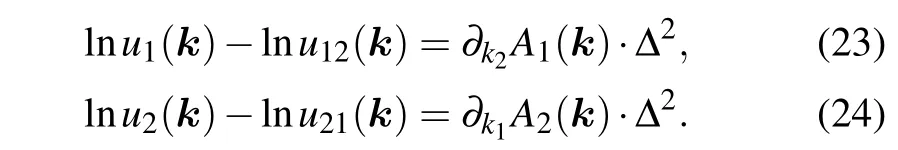
Thus we see that Eq.(20)is the discretized form of Eq.(15),and these two methods are equivalent.

3. Results and analyzing

In order to better describe the results, we set a fixed electric field asE0=γ0/(ea) throughout the paper. With otherE0values, we may have similar results. Figures 2(a)–2(b) show that in different driven frequencies, the graphene is in different topological phases with corresponding Chern numbers. We name the three topological phases as phase A(ħω＞5.96γ0), phase B (2.92γ0≤ħω ≤5.96γ0), and phase C (1.4γ0≤ħω ＜2.92γ0) in Fig. 2(b). In the Floquet calculations, we need to set a proper cutoff value (NF) due to the infinite dimension of the Floquet Hamiltonian. In Fig. 2, we draw the Chern number curves as a function of different driven frequencies withNF=1 andNF=2. We can see that the Chern number curves shown in Figs.2(a)and 2(b)are coincident in the region of 1.4γ0≤ħω ≤7γ0,while they are different in the region ofγ0≤ħω ＜1.4γ0. In this low-frequency range,more Floquet bands(or largerNFvalue)should be used for convergence. So we may conclude that in the frequency region of ħω ≥1.4γ0, the Chern numbers are converged withNF=1 and 2. Appendix A also shows that with ħω=1.4γ0,the band structures of GNR are converged only whenNF≥2. In this work, we just focus on the region of 1.4γ0≤ħω ≤7γ0, and we takeNF=2 throughout this paper. Figures 2(c) and 2(d)show the Berry curvature distributions withNF=2 and different ħωvalues. We can see that all the Berry curvature peaks are around the Dirac points.

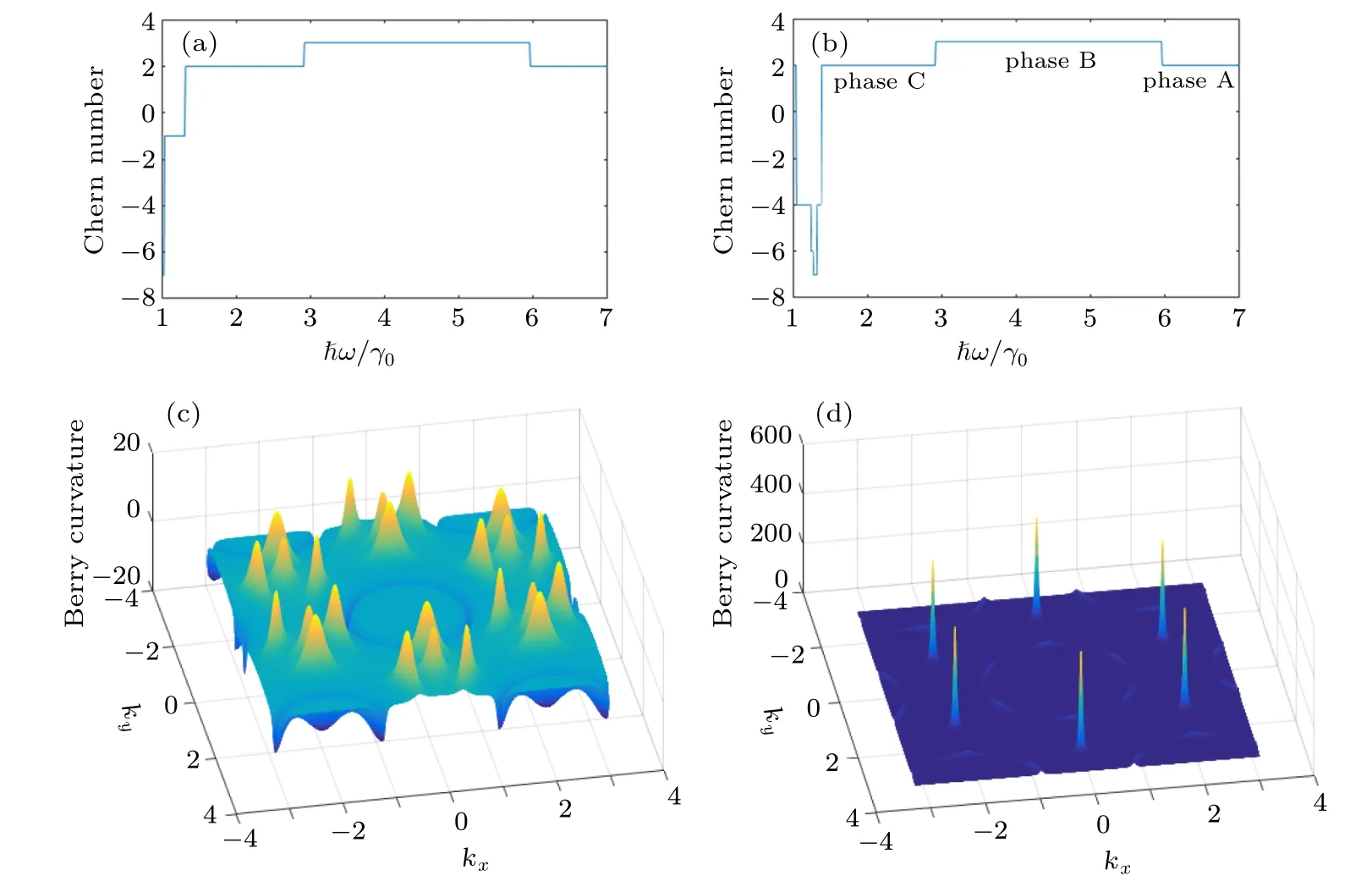
Fig.2. Chern-number phase diagrams with(a)NF=1 and(b)NF=2. Berry curvature distributions with different driven frequencies[(c)ħω=2γ0,(d)ħω=3.5γ0]in the Floquet graphene system(E0=γ0/(ea)).

In Fig.2,there are three topological phases in the region of 1.4γ0≤ħω ≤7γ0, with the Chern numbers of 2, 3, and 1. For zigzag GNR systems,these topological phases also exhibit the bulk–edge correspondence from the band structures.Figures 3(a)–3(c)show the results. We can see that under the radiation,there appear some edge-state bands across the original gap near the zero energy (called as 0-gap). And there appears a new dynamic gap aroundE=±ħω/2 with some edge-state bands across this gap.[9]This new gap results from the anti-crossing of the two intersecting band replicas(with the photon numbersn=0 andn=±1),due to the coupling Floquet matrices. This gap is called theπ-gap since it is similar to the gaps near the Brillouin zone boundary.[22]In Fig.3(a),with ħω= 7γ0we see that there just exists one edge state(red line) within 0-gap in the upper GNR edge. In Fig. 3(b)with ħω=4γ0,there are not only one pair of edge-state bands within 0-gap,but also two pairs of edge-state bands withinπgap. And in Fig.3(c),there are two types of edge states bands within 0-gap(one in the middle and one at the two sides of the band range[0,2π/b]).

Here we show that the bulk–edges correspondence also holds in the graphene system under different radiation frequencies.We define the net chirality of edge states in the upper edge as the winding number,denoted asW0(in 0-gap)andWπ(inπ-gap). The net chirality is the sum of the edge-state numbers, which is positive for the positive slope of the band; and negative for the negative slope of the band. Then we calculatec=Wπ −W0, wherecis the Chern number of the band between 0-gap andπ-gap.[10,27]Table 1 lists all these quantities in the three phases. We can see that the calculated Chern numbers agree well with our numerical results in Fig.2(b).

Table 1. The winding numbers and Chern numbers in different topological phases of GNR.

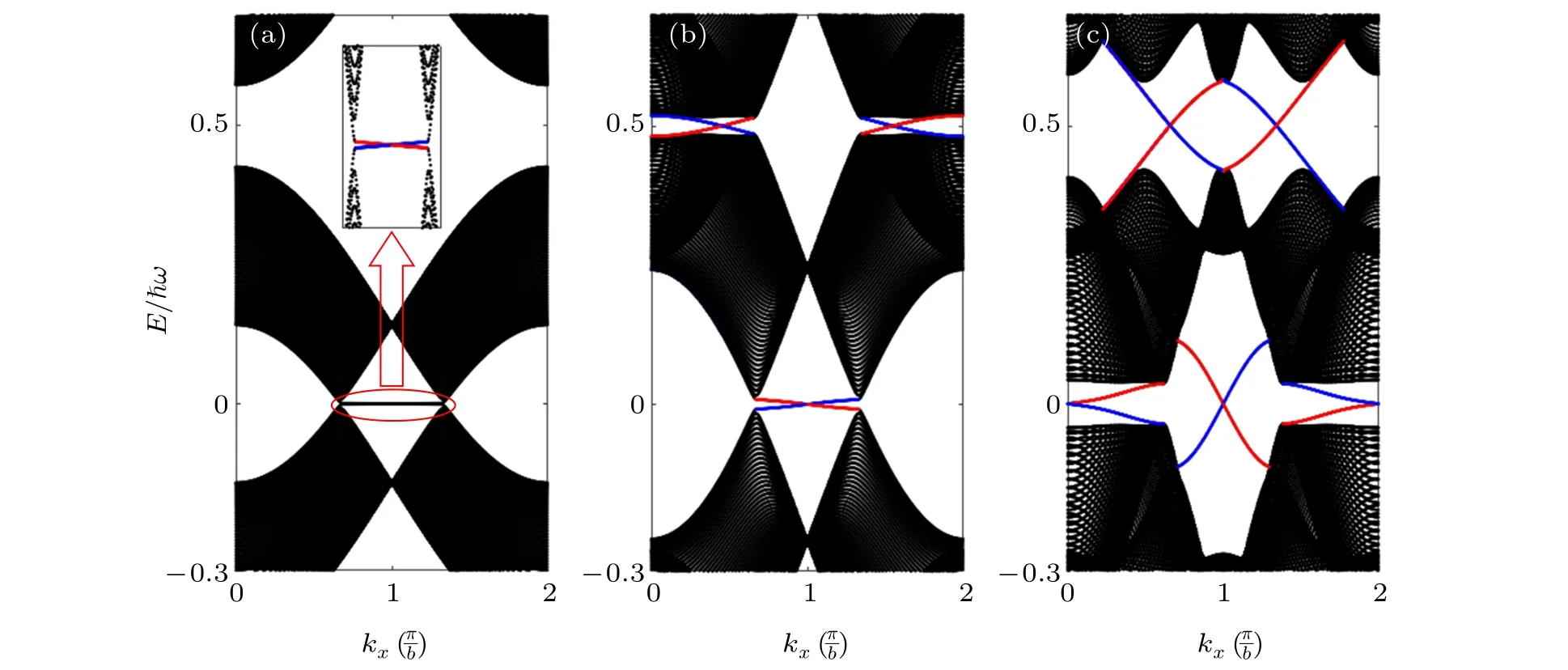
Fig.3. Quasienergy spectra of zigzag GNR with the size Ny=40 at different driven frequencies: (a)ħω =7γ0;(b)ħω =4γ0;(c)ħω =2γ0. The red lines denote the upper-edge states,and the blue lines denote the lower-edge states.

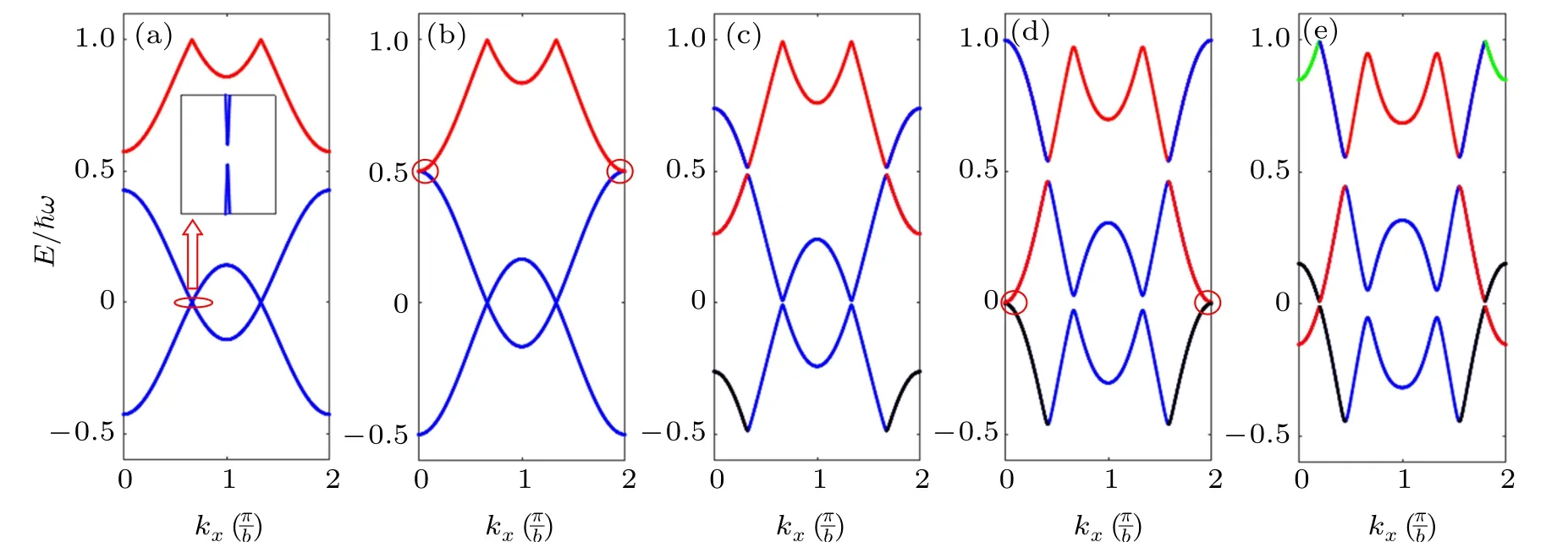
Fig.4.Projected 2D band structures of Floquet graphene system with different frequencies(ky=0):(a)ħω=6.5γ0,(b)ħω=5.96γ0,(c)ħω=4γ0,(d)ħω =2.92γ0,(e)ħω =2.5γ0. The different colors denote different Floquet bands,for example,blue: n=0;red: n=1;black: n=−1;green:n=2. The circles in(b)and(d)denote the band close(touching)regions between n=0 and n=1,or n=−1 and n=1 replicas,respectively.

In order to explain the topological phase transition as a function of frequency,we show the Floquet band structures in Fig.4. We use the projected band structures from the 2D Floquet bands for a clear view. In Ref.[28], it was reported that the 0-gap orπ-gap close and reopening means the occurrence of a topological phase transition. In Fig. 4(a), the frequency lies in the phase A range (see Fig. 2(a)). It shows that there is almost no coupling betweenn= 0 andn= 1 (−1) Floquet bands(replica). Then as the driven frequency decreases,the Floquet bands approach to each other and in some critical stage,n=0 andn=1 (−1) replicas tend to get touched and theπ-gap almost closes(Fig.4(b)). But when further reducing the frequency,theπ-gap is reopened(Fig.4(c)),which means the topological phase transition(from phaseAto phaseB)happens. From the colored bands in Fig.4(c), we can see that then=1 andn=0 Floquet bands are intersected nearπ-gap and are anti-crossed near the cross-points. With the similar analysis,from Figs.4(c)–4(e),there exists a gap close and reopening near 0-gap. Therefore,phase B is transformed into phase C.In Fig.4(e), we also see that the corresponding coupled (hybrid) band near 0-gap is withn=1 andn=−1 replicas. As will be seen in Fig. 5 later, these coupled Floquet bands will result in different edge state distributions in the decomposed photon-number space.

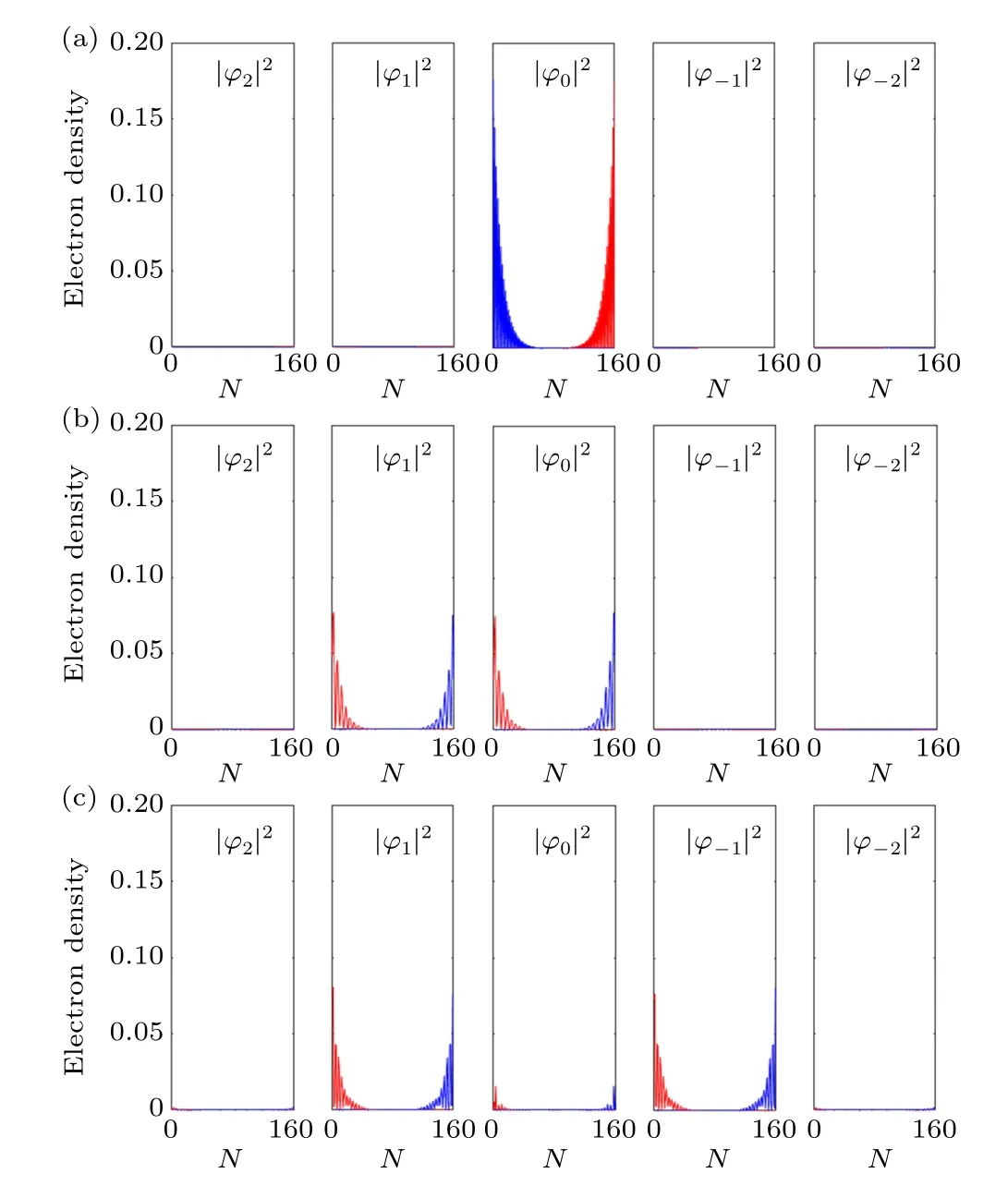
Fig. 5. Electron density distribution of edge states in GNR in the decomposed photon-number space (Ny =40) (a) The edge states in 0-gap with ħω =7γ0. (b)The edge states in π-gap with ħω =4γ0. (c)The edge states in the side parts of 0-gap with ħω =2γ0. The red lines denote the situation of dE/dk ＞0,and the blue lines denote dE/dk ＜0.

Next we show the electron density distribution in the decomposed photon-number space to analyze the origin of the edge states. In Fig. 5(a), the density distribution of the edge states within 0-gap (shown in Fig. 3(a)) only exists inn=0 Floquet photon number space,which means there is no photon resonance. In Fig.5(b),we plot the density distributions of the edge states withinπ-gap(shown in Fig.3(b)).We find they exist inn=0 andn=1 photon number space,which clearly indicates that the edge states originate from the one-photon resonance of the light. It also agrees with the hybrid 2D Floquet bands in Fig. 4(c), wheren=0 andn=1 replica bands are coupled and anti-crossed nearπ-gap. Similarly, in Fig. 5(c),the density distribution with respect to the edge states within 0-gap in Fig. 3(c) mostly exists inn=−1 andn=1 photon number space and only a small amount inn=0 photon number space, which means the edge states are mainly from the two-photons resonance and secondarily from two constructive one-photon resonances. We notice that Kang,Park and Moon also found such resonances in the Floquet bands of black phosphorene systems recently.[23]And these edge-state density distributions are also consistent with the hybrid 2D Floquet bands in Fig.4(e).

At last, we give a discussion on the size effect of these Floquet edge states. All the band structures in Fig. 6 are in phase B. When ħω=5γ0, we find with increasing the ribbon width,theπ-gap and the edge states in this gap are gradually formed(see Figs.6(a)–6(c)). From this,we see that although there existsπ-gap for bulk graphene as long as the frequency lies in the phase B range (2.92γ0≤ħω ≤5.96γ0), the GNR band can exhibit this gap and the corresponding edge states only with the large-enough ribbon width. We also observe this size effect for the frequency ofω=5.8γ0(Figs. 6(d)–6(f)).Compared to the ones in Figs. 6(a)–6(c), a larger width is needed to generate theπ-gap and the edge states since the frequency is close to the topological transition point (ħω=5.96γ0). So the size effect plays an important role in the GNR Floquet systems,especially for the frequency close to the transition point.

Fig.6. Size effect for energy bands of GNR under light radiation with different ribbon widths: (a)–(c)ħω=5γ0,(d)–(f)ħω=5.8γ0.

4. Conclusion

To summarize,we have investigated the phase transitions of graphene under light irradiation,and verified the bulk–edge correspondence by calculating the Chern number and analyzing the winding numbers of edge states in the Floquet gaps.We also have used the projected 2D Floquet bands and GNR

1D bands to analyze its density distributions in the decomposed photon-number space. The origin of the Floquet edge states has been discussed. The size effect in the GNR system is important and becomes strengthened when the driven frequency is close to the phase transition point.

Appendix A

To further demonstrate the reliability of our calculations,we give an example for the photon number convergence in GNR band calculations. We use differentNFvalues and plot the corresponding GNR bands below. The low driven frequency (ħω=1.4γ0) on the lower boundary of phase range C is used.

In Fig. A1, we see that the Floquet band withNF=2 is almost as the same as that withNF=3. ButNF=1 is vastly different, especially inπ-gap. Let us explain it more theoretically. In the Floquet Hamiltonian matrix(Eq.(5)),the coupling matrix elementHnis proportional to the Bessel functions of the first kindHn∝Jn(z)withz=eA0a/ħ.

Fig. A1. Quasienergy spectra of zigzag GNR (Ny =40) with different NF values: (a)NF =1; (b)NF =2; (c)NF =3. The corresponding parameters E0=γ0/(ea)and ħω =1.4γ0.

Becausez=E0/ħω ≈0.7 in our example, we see thatJn(z)is small enough to be ignored when|n|≥2(Fig.A2(b)).Then according to Fig.A1,we can conclude that the result ofNF=2 is reliable enough with 1.4γ0≤ω ≤7γ0. Meanwhile,we emphasize here that there needs an even largerNFvalue to insure the accuracy and converge of Floquet band calculation when the driven frequency is further smaller. The cut-off value can be estimated from the Bessel function variations in Fig.A2.

Fig.A2. (a)The behaviors of the Bessel functions of the first kind(Jn(z),n ∈[0,4]). (b)The Bessel functions Jn(0.7)with different n values.