基于构造物理模拟实验的正断层形成和演化过程

彭先锋, 邓虎成*, 胡笑非, 张烨毓, 张小菊

(1.成都理工大学能源学院， 成都 610059； 2.四川省科源工程技术测试中心， 成都 610091； 3.页岩气评价与开采四川省重点实验室， 成都 610091)

断层的形成和演化一直是裂陷盆地构造研究的核心，也是裂陷盆地油气勘探的关键[1-4]，含油气盆地内断层多数是以断裂带的形式存在，探讨正断层形成和演化过程对研究油气沿断裂带运移途径具有重要价值。针对正断层的形成和演化，前人已经作了大量有意义的探讨。一方面，依据经典的安德森(Anderson)模式，当差异应力大于岩石的破裂强度时，则会形成倾角为40°～70°的正断层。然而宏观上，安德森模式是建立在刚体受力基础上，自然岩层并非刚体，在构造变形过程中地质应力存在损失，裂隙的尖端区域发生应力集中使裂隙递进扩张形成优势主裂隙最终形成断层。因此，基于安德森模式分析正断层的形成和演化过程、探讨断裂带内部结构和确定断层进一步演化趋势等并不理想。另一方面，已有的研究表明：断层发育程度与储存于岩石中的应变能存在正相关关系。通过古应力场数值模拟技术计算每个单元的弹性应力变能，可以预测伴生裂缝的相对发育程度。同时这仅是一种相对或定性预测裂缝密度的方法[5]。Housner首先提出在地球物理学科中运用能量的概念[6]，紧接着地球物理学专家们从时域、频域角度对地层破坏的输入能特征做了大量的探讨[7]。从能量角度来说，正断层形成演化的实质是地层岩块中弹性能量的积聚和突然释放，正断层形成是最大变形和累积能量耗散共同作用的结果。近几年，中国学者通过声发射技术获得地层微破裂的时空展布规律，并基于此进行正断层失稳前兆、地震机理等相关问题的研究[8]。断层形成是由稳定的三向应力状态迅速向单向应力状态跃迁，地层失稳破坏所需要的能量难以直接测量[9]。实验测试方面，岩石物理实验着重研究小尺度岩石样本的力学性质，仅依靠适用于小变形范畴的库仑剪破裂准则对断层的形成演化进行解释，这种方法难以完善的解释断层此类力学上属于大变形范畴的构造变形问题[10-12]。数值模拟方面，普遍假设数值模型为线弹性或静态，且假设断层之外的岩石不发生破坏，因此不能模拟新破坏区产生过程以及断层形成过程中能量的变化特征，难以模拟断层复杂的演化行为。因此，针对正断层形成和演化的研究仍有待提高。

由于岩体是典型的非均质连续介质，含油大量结构不连续、形状不规则的裂隙、节理或断层，现有的应力强度理论与破坏准则难以有效分析岩体复杂的强度变化与整体破坏行为。因此，建立岩体破坏过程中的能量变化规律及其与破坏之间的关系，不仅更加接近地层岩石破坏的本质[13]，而且更适合研究地层岩块破坏的空间分布规律[14]。首先通过构造物理模拟实验模拟正断层的形成和演化过程，然后分析此过程中断层倾角、断层距离随演化进程的变化规律，明确断裂带(断层面、断层破碎带)内部变化特征，划分正断层形成和演化的关键时期；其次依靠粒子成像测速技术，分析正断层带内岩石蕴含的应变能变化特征；最后，从物质破坏的本质，即地层内能量变化的角度探讨正断层形成和演化过程。需要强调的是，正断层形成的构造背景有背斜构造的局部、地层差异升降、岩层重力滑动和地层区域性水平拉伸[15]。研究主要探讨油气勘探中常见的、对油田开发影响较大的地层区域性水平拉伸条件下产生的正断层形成和演化过程，以及其形成和演化中岩石蕴含的应变能变化特征。虽然设计的构造物理模拟模型仅限于地层区域性水平拉伸产生的正断层，但是此类正断层最为常见，同时研究成果对逆断层、平移断层的类似研究可能会带来一些新的启示。

1 实验系统和方法

1.1 实验系统

1.1.1 实验装置

成都理工大学油气藏地质及开发工程国家重点实验室“地质构造变形物理模拟综合实验台”。该实验台可实现三维空间内多方向加载施力。实验装置由模型仓、控制系统、摄像系统和液压系统4个模块。

1.1.2 实验材料

材料为干燥石英砂。干燥石英砂是普遍采用的模拟浅层地壳脆性构造变形材料[16-22]。干燥石英砂变形遵循莫尔一库仑破坏准则，内摩擦角为31°左右，与地层岩石内摩擦角相近[18]。对于大量颗粒组成的受限体系，可仿照连续介质，用等效弹性模量描述其软硬程度，因此在岩石力学上，使用松散石英砂模拟沉积岩层可行的[23]。实验选用的干燥石英砂为纯白色高纯度干燥石英砂(二氧化硅的质量分数大于99%，主要杂质为三氧化二铁)，密度为1.35×103kg/m3，粒径为300～450 μm，内摩擦角为30°，内摩擦系数为0.56。前人研究研究表明，根据相似系数换算到对应模型材料的强度差别很小，因此设计模拟实验时不考虑岩石层间差异性。

1.1.3 实验参数

由于模拟仓大小是固定的，本次实验优先考虑几何相似，使模拟仓尺寸满足相似性、便于仪器加工装配和实验操作。实验参数遵循模型与原型的相似性，主要包括几何相似、动力相似和运动相似，同时具有一致的流变属性和变形比例[16,22]。实验参数设计见表1。

1.1.4 实验设计

实验模型参考Cloos提出的张性构造模型[24]。

基底和边界均设定为刚性，采用玻璃挡板模拟。为了能够使拉力上传到模型上部产均匀拉伸，拉伸地层采用均匀涂抹硅胶的有机硅粗帆布模拟，帆布为涤纶纤维织造，厚度为0.7 mm。模拟仓内石英砂从上到下厚度分别为15、15、20 mm。铺设l.0 mm厚的彩色石英砂(染色后的石英砂不改变其物性)薄层插入模型作为标志层，方便实验者观察和测量模拟仓内的构造变形过程。在模型上方和正前方布置摄像系统记录实验结果，如图1所示。

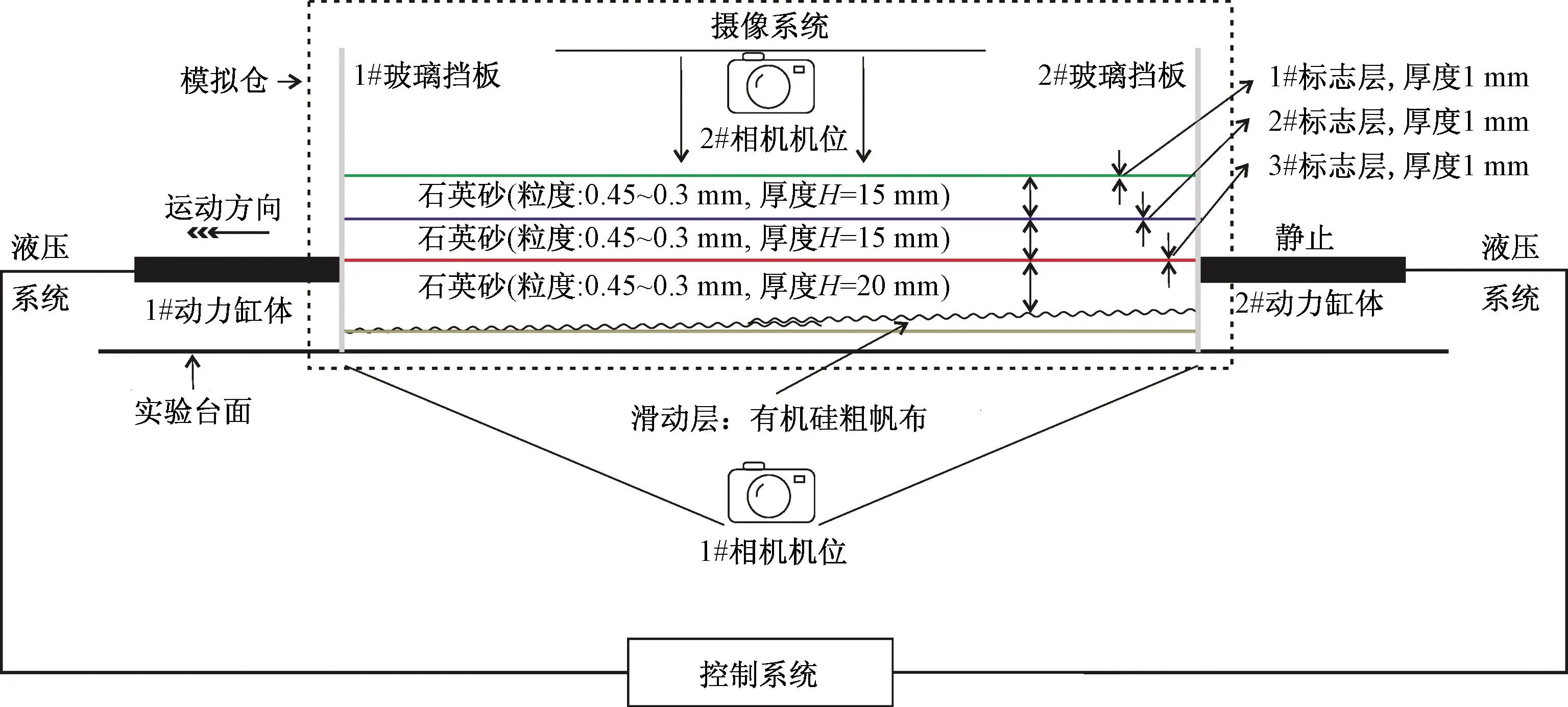
图1 构造物理模拟实验装置示意图Fig.1 Schematic diagram of the structure physical simulation experiment device

1.1.5 实验步骤

右端动力缸体固定，在1#动力缸体施加的水平拉伸力作用下，左端动力缸体匀速(V实验=0.005 mm/s；L总拉伸量=100 mm)拉伸固定在挡板底部的帆布，对模拟仓砂层施加拉伸力模拟地层水平伸展运动，模拟仓内砂层形成正断层(图2)。重复实验4次避免偶然因素影响实验精度并验证实验结果的可重复性。

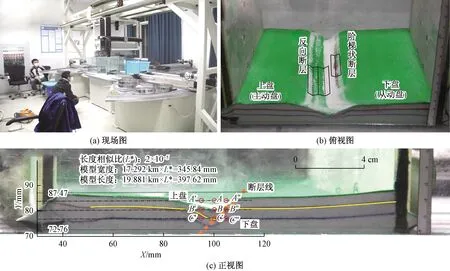
A(100.87，83.79)、B(100.87，80.11)、C(100.87，76.43)为断层破碎带内3个观测点；A′(95.34，83.79)、B′(95.34，80.11)、 C′(95.34，76.43)和A″(104.54，83.79)、B″(104.54，80.11)、C″(104.54，76.43)为断层面两侧裂缝发育带内的观测点图2 构造物理模拟实验过程图Fig.2 Process diagram of structural physical simulation experiment

1.2 数据采集与处理

粒子图像测速技术(particle imaging velocity，PIV)，使用数字相机拍摄片光照明流场照片得到前后两帧粒子图像，对图像中的粒子图像进行精密的互相关计算，得到流场内一个切面内定量的速度场分布数据，再通过数据处理(Tecplot 360)得到各点的速度以及速度场云图如图3所示。

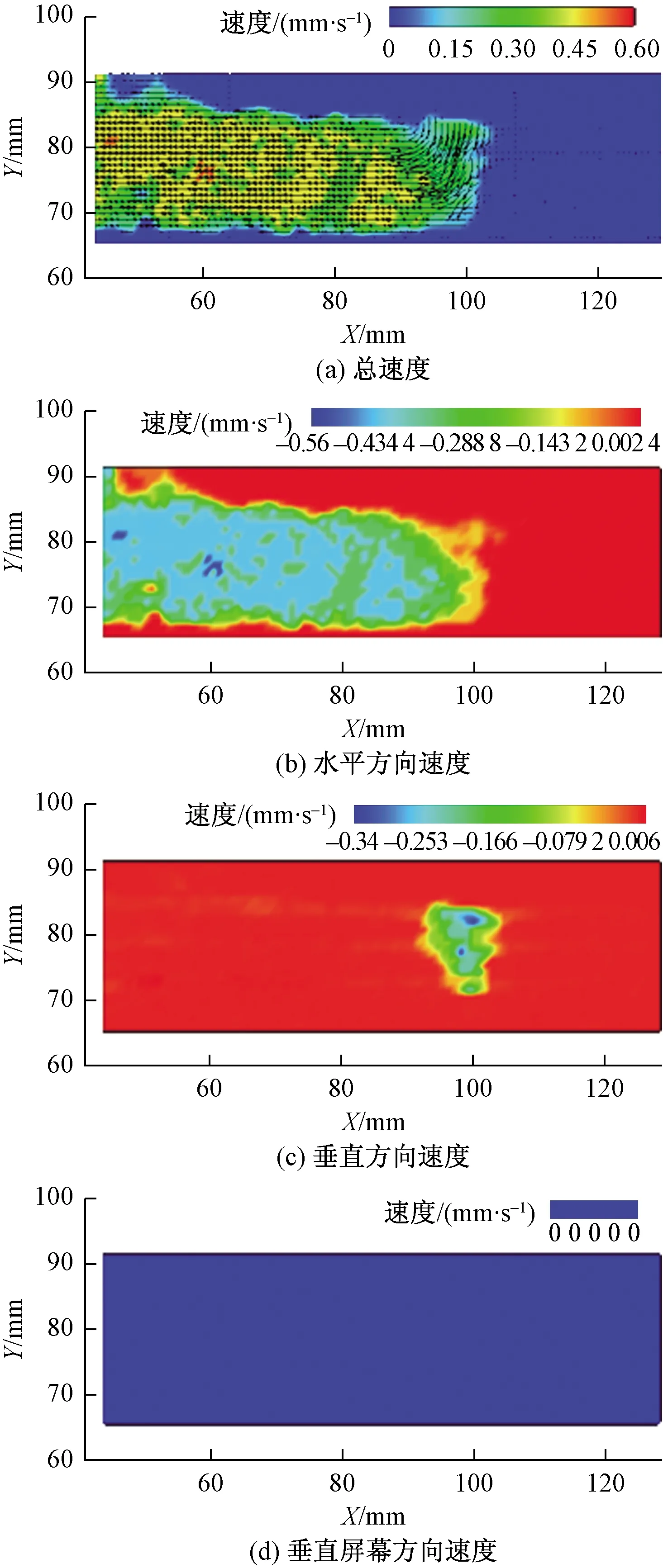
图3 总速度、水平方向速度、竖直方向速度、 垂直屏幕方向速度的速度场云图Fig.3 Cloud diagram of velocity field of total velocity, horizontal velocity, vertical velocity, and vertical screen direction velocity

实验每隔30 ms采集1次实验数据，实验过程中玻璃挡板不可避免会出现轻微的震动、试验台的震动，以及模拟仓内砂层的顶面空气扰动等都会影响粒子成像测速技术的精度，因此，本次实验舍弃玻璃挡板附近2 cm内和模拟仓砂层顶面1 cm内粒子成像测速数据，以保证实验数据的真实性。

2 实验结果

2.1 倾角的形成和演化

断层线与水平投影线之间的夹角称为倾斜角。在本次实验中，根据实验得到的速度场(图3)，计算倾角的公式为

(1)

式(1)中：α为倾角，(°)；v为竖直方向速度，m/s；u为水平方向速度，m/s。

实验模拟仓设计为水平受力，即v= 0，因此模拟仓内砂层未产生断裂前α=arctan(v/u)=arctan(0/u)=0°，所以α≠0°是模拟仓内砂层各测量点断裂产生的标志，倾角的绝对值反映了断裂程度的大小。分析正断层形成演化阶段各个测量点断裂倾角的变化特征(图4)，可知：α≠ 0°现象最先在模拟仓内砂层的顶(65.40 mm)、底(91.15 mm)位置出现，表明砂层最先产生破裂的位置为顶、底部位，并不是砂层的内部[图4(a)～图4(c)]。随着实验进行、拉伸量(L拉伸量)逐渐增大，砂层中上部(83.79 mm)出现α≠0°现象并向下延展，正断层有“自上而下”破裂产生断层面的趋势[图4(d)]。断层面产生后，随着L拉伸量进一步增大，断层面内倾角变化杂乱无章，无明显规律[图4(e)～图4(h)]。

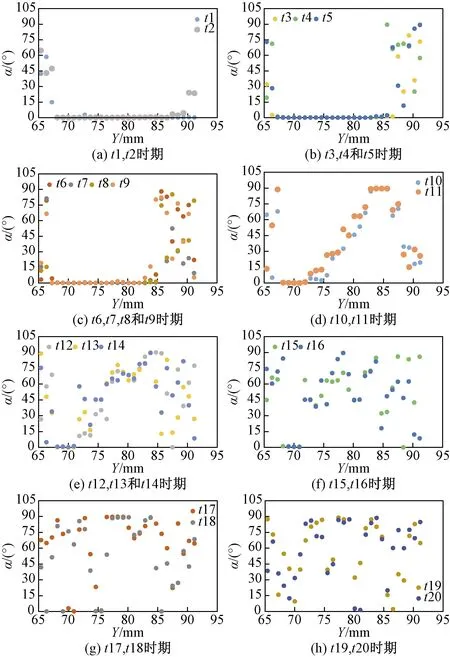
图4 不同时期的正断层断裂倾角位置分布Fig.4 Distribution of normal fault dip angles in different periods

通过实验可知，模拟仓内断层面产生位置为X=105.46 mm(图2)。断层面内断层主要发育高角度倾角(65°<α≤90°)，表明强变形区域集中于剪切面(图5)；将断层面两侧外推一个单元格所夹持的范围定义为断层破碎带(104.54～106.38 mm)，断层破碎带内各个测量点断裂倾角(α)和埋深(L)呈指数函数关系，即随着埋深(L)的增加，倾角(α)逐渐减小(图6)；将断层面两侧外推三个单元格所夹持的范围定义为裂缝发育带(102.70～107.30 mm)，裂缝发育带内，距离断层面等间距位置的断裂倾角(α)随埋深(L)有“多期递减”现象，表明正断层及其伴生裂缝的发育程度不仅和距离断层的距离(D)相关，而且受到埋深(L)的控制(图7)。将断层面两侧外推三个单元格以上范围定义为损伤带。受到断层构造影响并产生破裂的损伤带内断裂倾角(α)在70°～90°为35%，0°～10°为14%，高角度和低角度为优势倾角范围(图8)。

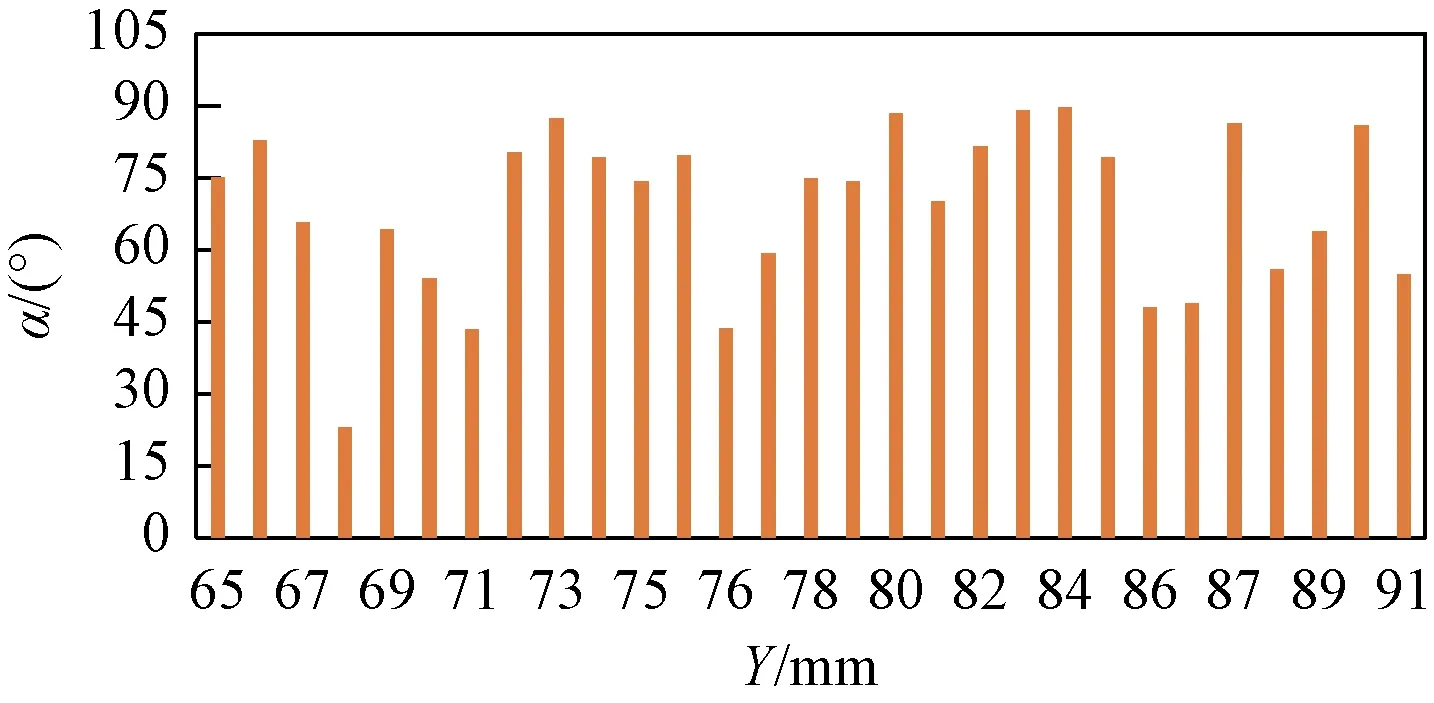
图5 断层面内倾角分布图Fig.5 Distribution of the dip angle in the fault plane

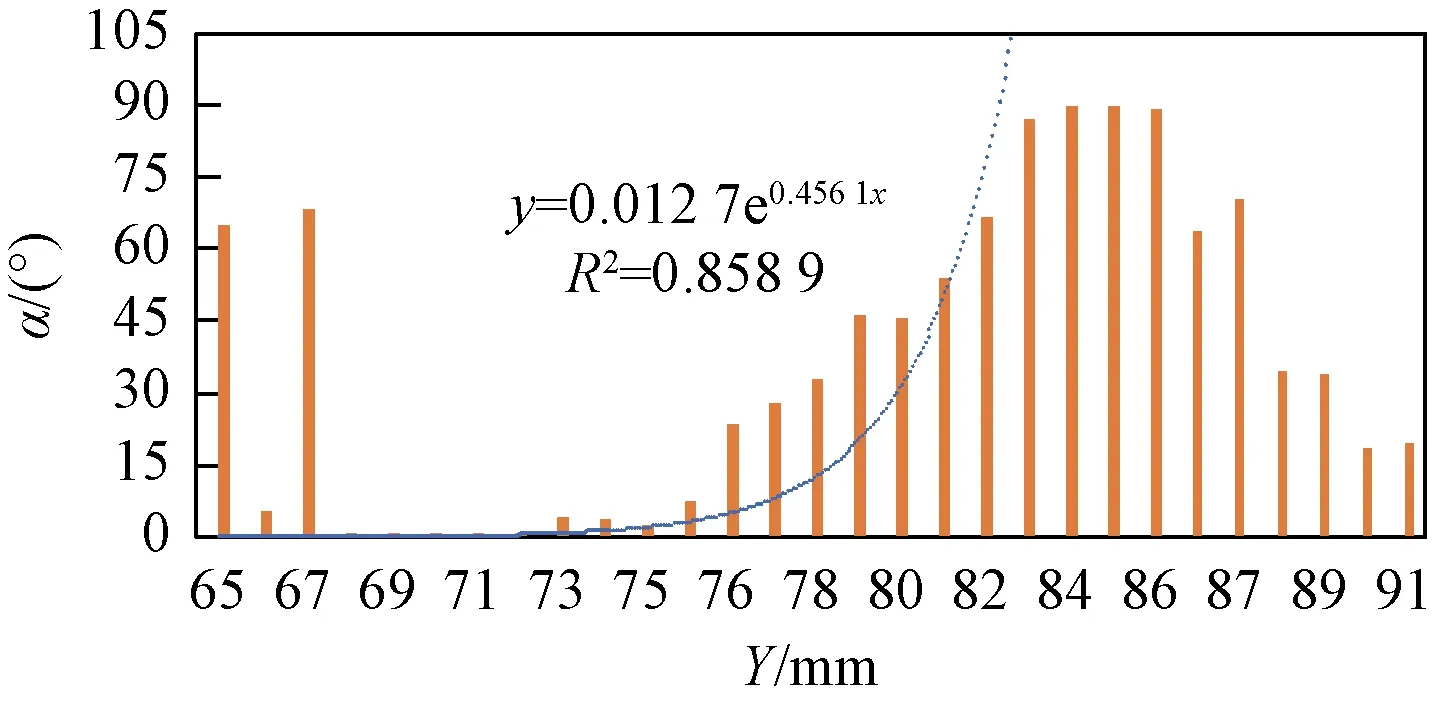
图6 断层破碎带内倾角随埋深关系Fig.6 Relationship between the dip angle in the rupture zone and the buried depth

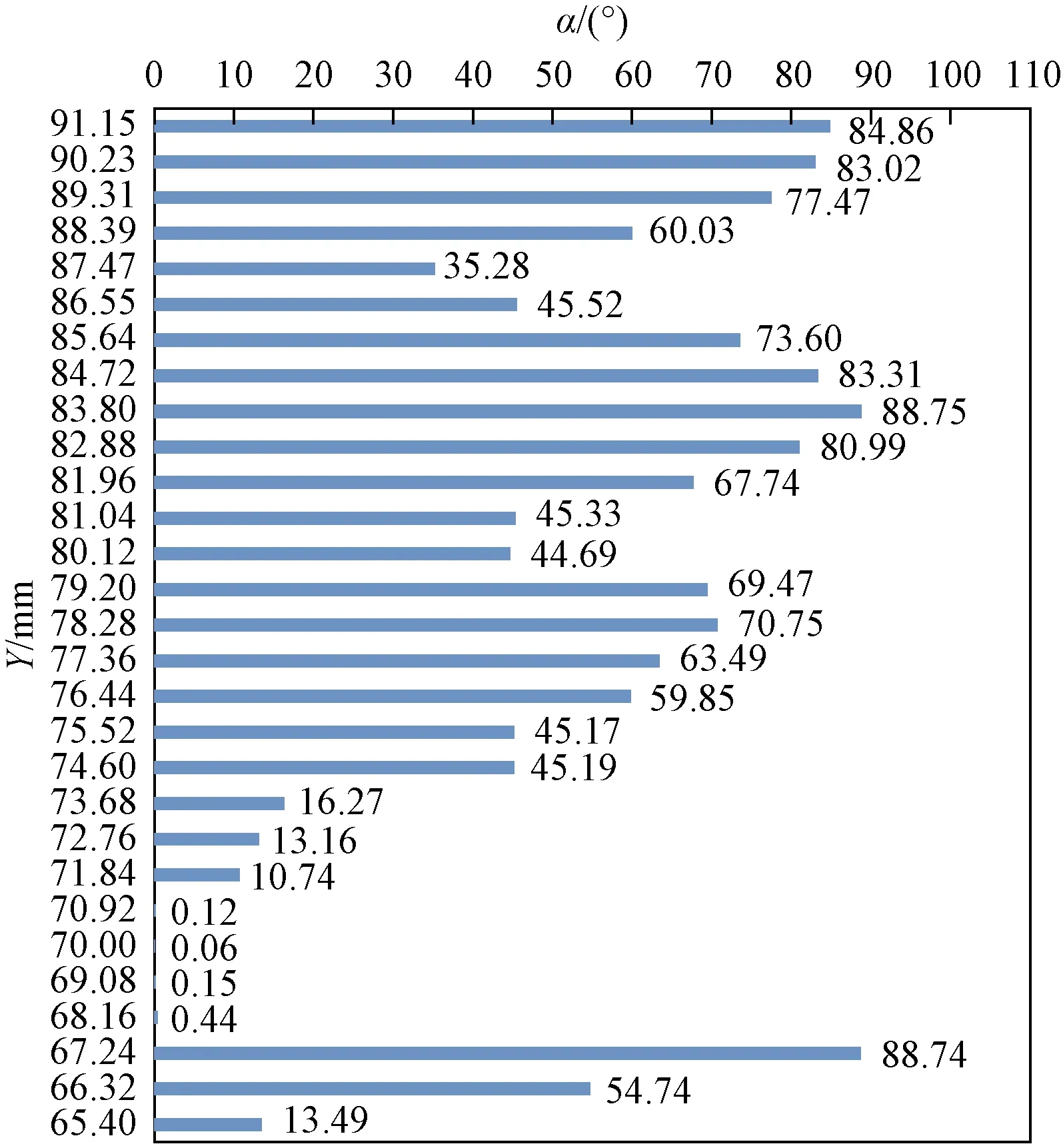
图7 裂缝发育带内断层倾角与埋深的关系Fig.7 The relationship between the dip angle in the fracture zone and the buried depth

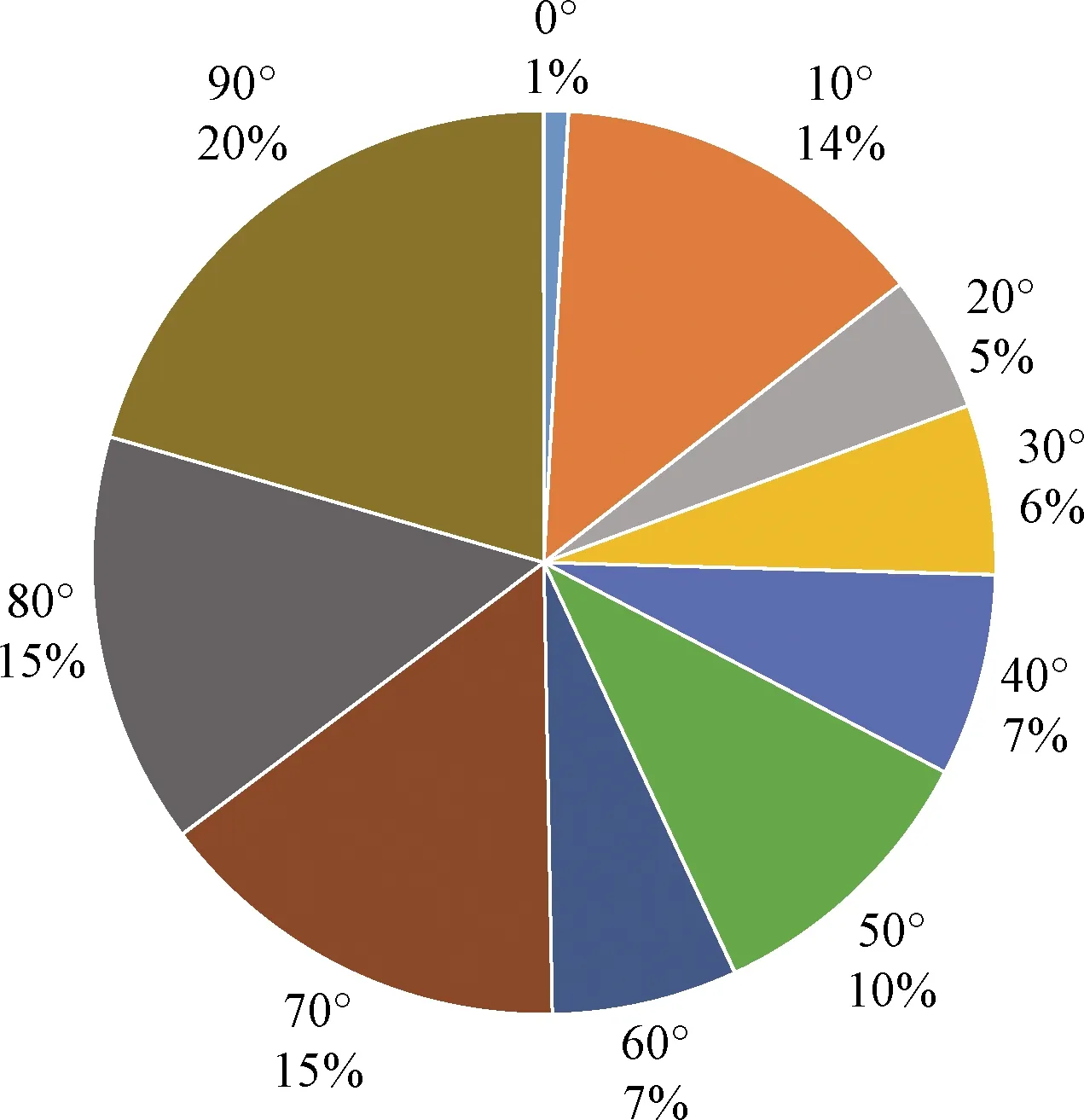
图8 损伤带内的倾角分布Fig.8 Distribution of the dip angle in the damage zone

2.2 断层距离的形成和演化

断层上、下盘上同层位两点位移后的垂直距离叫断层距离或断距。基于实验获得的总速度云图(图3)，通过Tecplot 360软件计算得到横向上相邻两观测点之间的断距(ΔL)，即

ΔL=S(i+1，j)-S(i，j)=[Vz(i+1，j)-Vz(i，j)]Δt

(2)

式(2)中：ΔL为横向上相邻两观测点之间的断距，m；S(i+1，j)，S(i，j)为横向上相邻两观测点的位移量，m；Vz(i+1，j)，Vz(i，j)为横向上相邻两观测点的总速度，m/s；Δt为实验记录间隔，30 ms。

按照表1设计的空间尺度相似比(L*)将正断层构造物理模拟模型断距换算成地质原型断距，以方便与油气田内的真实断距相对比。统计正断层不同形成演化时期的断距(ΔL)可知：模拟仓内砂层中上部最先出现明显断距(ΔL)；随着拉伸量(L拉伸量)的增大，断距(ΔL)不断增大，断裂向砂层下部延展；断层下部断距大、断裂程度明显大于上部；断层成核的起点在中上部断层段，下断层段的错动是由中上部断层段错动触发引起(图9)。断距并不均等，分布范围为4.66～16.31 m，断距的双峰值分别为15.23 m和16.31 m，断距分布呈“双峰”特征(图10)。

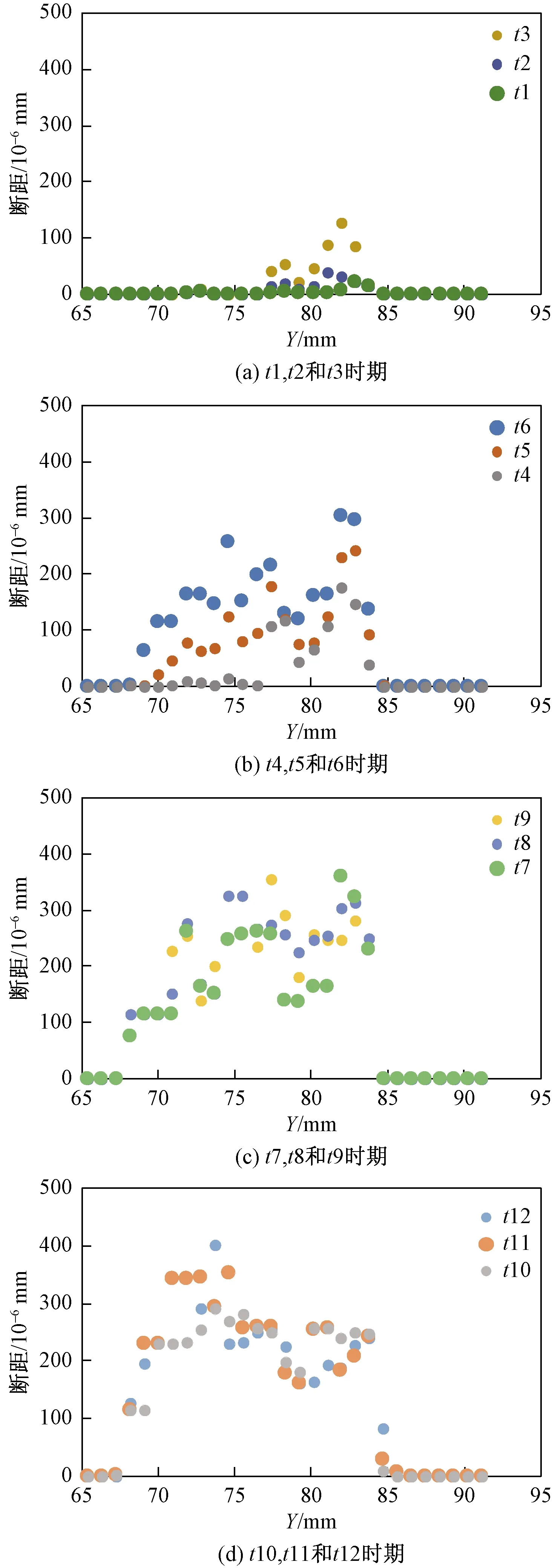
图9 不同时期的正断层断距分布Fig.9 Distribution of the normal fault displacement in different periods

3 讨论

以应变和应力的形式贮存在物体中的势能即为应变能，又称变形能。对于释放的应变能，可以利用多种方式进行统计，例如统计其时空分布规律、密度、总量、释放率，频次-能量关系等的演变规律[25]。正断层发育模式和形成演化的实质是地层岩石中弹性能量的积聚和突然释放过程，其形成是最大变形和累积能量耗散共同作用的结果。在水平拉伸力作用下，可以将运动微分方程转变为能量平衡方程[26]。单自由度体系的运动微分方程为

(3)

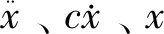
式(1)各项对相对位移x，在时间[0，t]内积分，得到单自由度体系的相对能量平衡方程，即

(4)

式(4)中：EI为地层岩块积累的应变能，J；Ek为地层岩块的相对动能，J；ED为地层岩块的阻尼耗能，J；EH为地层岩块的滞回耗能(结构变形能)，J；m为单自由度体系质量，kg；veq为单自由度体系内的速度，m/s。

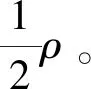
(5)

式(5)中：w为应变能密度；σij为各个方向的应力分量；εij为各个方向的应变分量；ρ为单自由度体系中岩石密度；V为地层岩块的总体积。

3.1 正断层形成和演化的阶段

以模拟仓的拉伸量(L拉伸量)变化量划分正断层模型的形成演化阶段；以正断层模型中心位置的应变能密度(w)曲线突变点作为划分正断层形成演化阶段的标志(图11)。正断层形成演化阶段可划分为断层初始期、断层孕育期、断层形成(Ⅰ、Ⅱ和Ⅲ)期、断层稳定期4个主要时期。断层初始期(L拉伸量=0～3.825 mm)，正断层模型中心位置开始出现应变能密度缓慢增加现象，应变能密度小于0.003×106J/m3。断层孕育期(L拉伸量=3.825～6.12 mm)，应变能密度快速增加，达到断层初始期的33倍，平均应变能密度为0.099×106J/m3。断层形成Ⅰ期(L拉伸量=6.12～7.65 mm)，应变能经过孕育期的不断积累，平均应变能密度达到峰值(wmax1=2.218×106J/m3)后开始释放，随着应变能释放，应力差逐渐变小，当其趋向于零或小于滑动阻力时，一次断层作用即告终止；wmax1为应变能持续积累后首次释放的破裂极限值，模拟仓内砂层剖面观察到局部断裂现象。断层形成Ⅱ期(L拉伸量=7.65～9.18 mm)，随着应变能释放后的再次积累，观察到局部未贯穿断裂面，断层形成进入Ⅱ期；Ⅱ期应变能密度峰值(wmax2=5.140×106J/m3)是Ⅰ期应变能密度峰值的2.3倍，表明地层发生大规模断裂时能量积累难度大于发生小规模断裂。断层形成Ⅲ期(L拉伸量=9.18～10.71 mm)，Ⅲ期应变能积累量最大，释放率最高，观察见贯穿断裂面；应变能密度峰值(wmax3=8.024×106J/m3)，是Ⅰ期应变能密度峰值的3.6倍，是Ⅱ期应变能密度峰值的1.5倍；断层形成期划分为3个亚期，“亚期”之间应变能密度增量近似相等，分别为2.922×106J/m3和2.884×106J/m3。断层稳定期(L拉伸量=10.71～15.3 mm)，地层应变能密度保持基本稳定，平均应变能密度为0.406×106J/m3；虽然断层进入稳定期，但是地层应变能水平仍高于断层形成前(w<0.003×106J/m3)的水平。

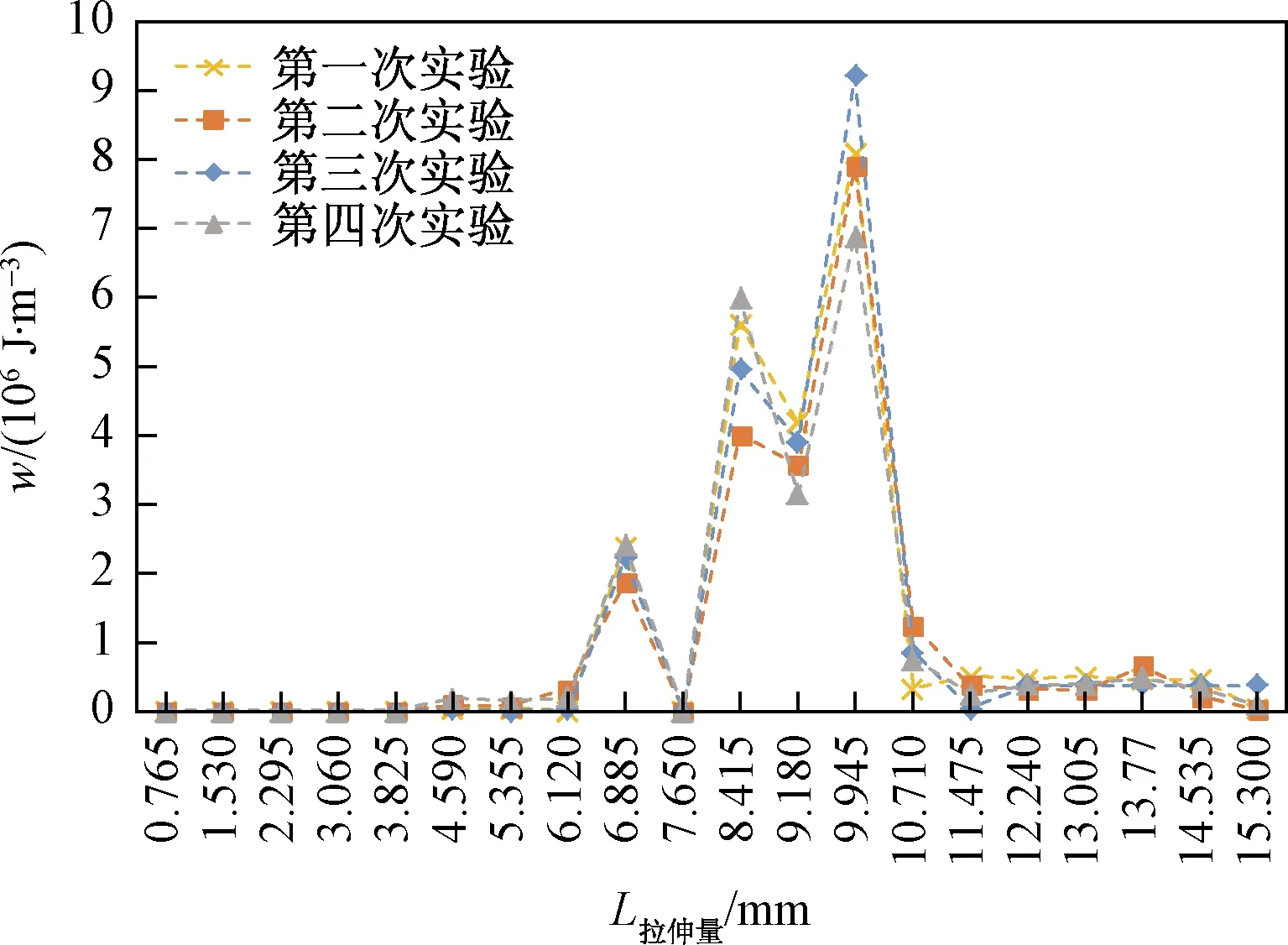
图11 正断层中心位置的应变能密度变化曲线图Fig.11 Variation curve of strain energy density at the center of normal fault

3.2 正断层带内岩石应变能变化特征

研究显示倾角是各测量点断裂产生的标志，其绝对值大小反映断裂程度强弱。断层面内倾角主要为高角度，显然断层面内断裂程度最为剧烈；断层破碎带内倾角和埋深呈指数函数关系，可以用埋深定量反映断层破碎带内断裂程度；裂缝发育带内倾角受到埋深、距离断层的距离两个因素控制。由于断层面相比断层破碎带和裂缝发育带规模较小，主要分析断层破碎带、裂缝发育带内应变能密度变化特征(图12，表2)。

表2 岩石内应变能释放时间、位置和峰值统计Table 2 Statistical of release time, position and peak value of strain energy in rock

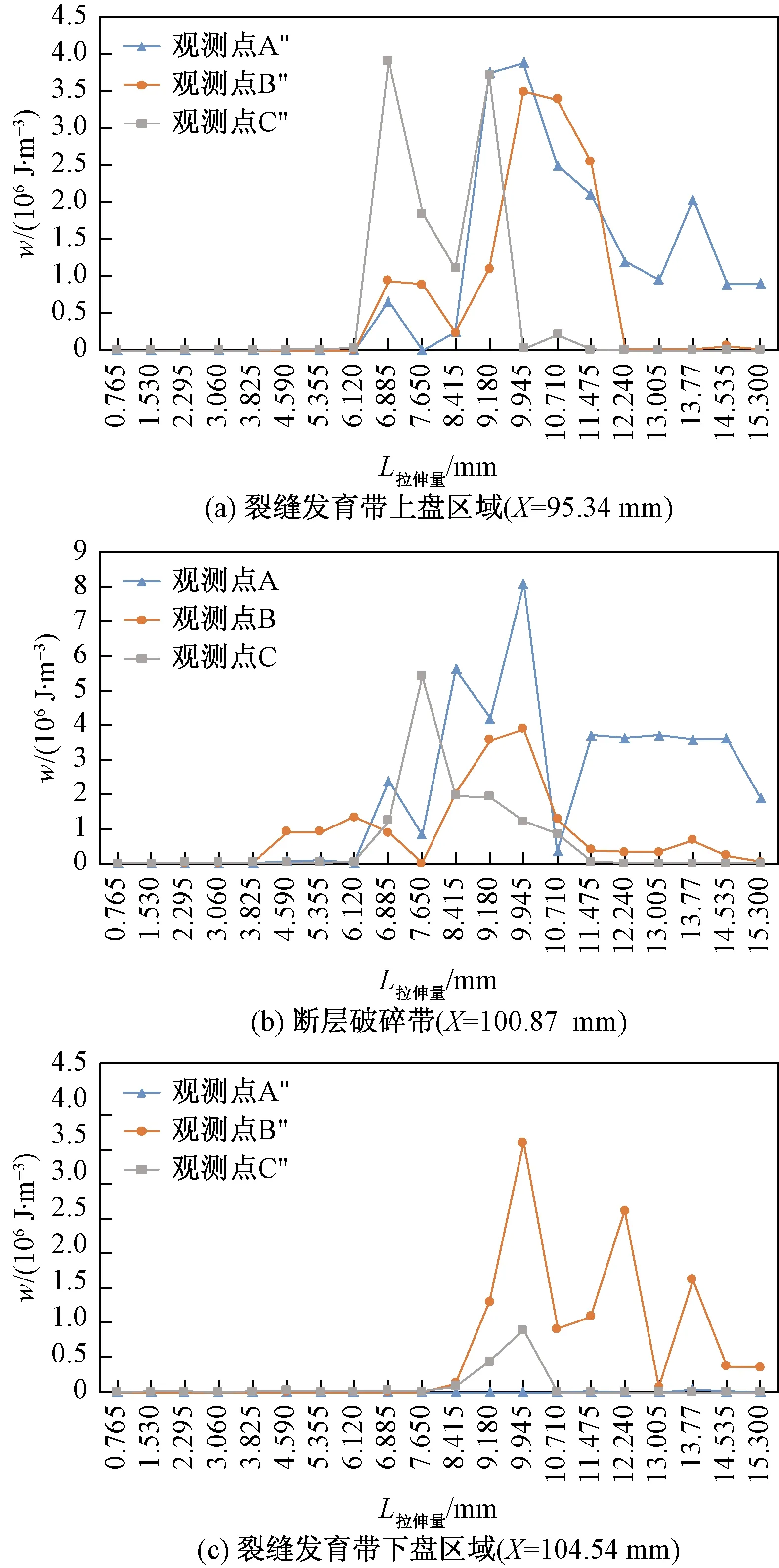
图12 断层破碎带、裂缝发育带应变能密度变化Fig.12 Variation of strain energy density of the rupture zone and the fracture zone

(1)裂缝发育带内应变能非均匀积累。断层上盘比下盘最先积累起明显的应变能。

(2)上、下盘应变能首次释放的时间、峰值、释

放率不同。下盘首次应变能释放的峰值小于上盘，时间晚于上盘，但释放率高于上盘。

(3)应变能在地层中部位置最先累积，其次是上盘，最后是下盘，断层的形成具有“自上向下”的延伸趋势。

(4)整体上，上盘区域为小规模周期性的应变能“积累-释放-积累”；断层破碎带首次应变能释放率最低，残留的应变能较高，应变能短时间积累后进入下一个能量释放时期；下盘区域首次应变能释放率高，需经历长时间应变能积累才能进行二次能量释放。

平面上，正断层形成前应变能最先在地层中部位置积累增加，地层中部位置具有最大的应变能积累速率并以此为中心递减。随着构造应力的不断作用，地层内积累起明显应变能的区域范围逐渐增大，此时积累的应变能值较小[图13(a)]。随着水平拉伸的不断作用，地层中有明显应变能积累的范围逐渐扩大，应变能值也逐渐增大。在应变能整体增大的同时，局部地层也有应变能释放现象，主要集中在断层面中部[图13(b)]。随着构造应力的不断作用，应变能沿断层面纵向深度不均匀释放，应变能最大释放区域位于断层面中部左右两侧，地层中部释放应变能的同时地层顶部、底部继续累积能量[图13(c)]。当积累的应变能大于地层所能承受的极限，地层发生破裂释放应变能，引发地层断裂和位置错动形成正断层。断层面形成后，应变能被断层面“塑性涂抹作用”消耗，此时应变能积累缓慢，断层面上下两侧各有一个应变能积累区域[图13(d)]。应变能首次释放后，由于“塑性涂抹效应”消耗应变能，断层面以下为能量释放，断层面以上为应变能积累，应变能释放区域和积累区域范围均不断向下发展，断层进入生长期，断距增大[图13(e)]。正断层形成后，断层下盘顶部区域处于裸露状态的范围不断扩大，不宜积累应变能，断层下盘应变能积累范围不断缩小，断层下盘区域内的地层逐渐趋于稳定。断层上盘区域受到构造应力的不断作用，一直处于应变能积累和释放的活跃状态[图13(f)]。

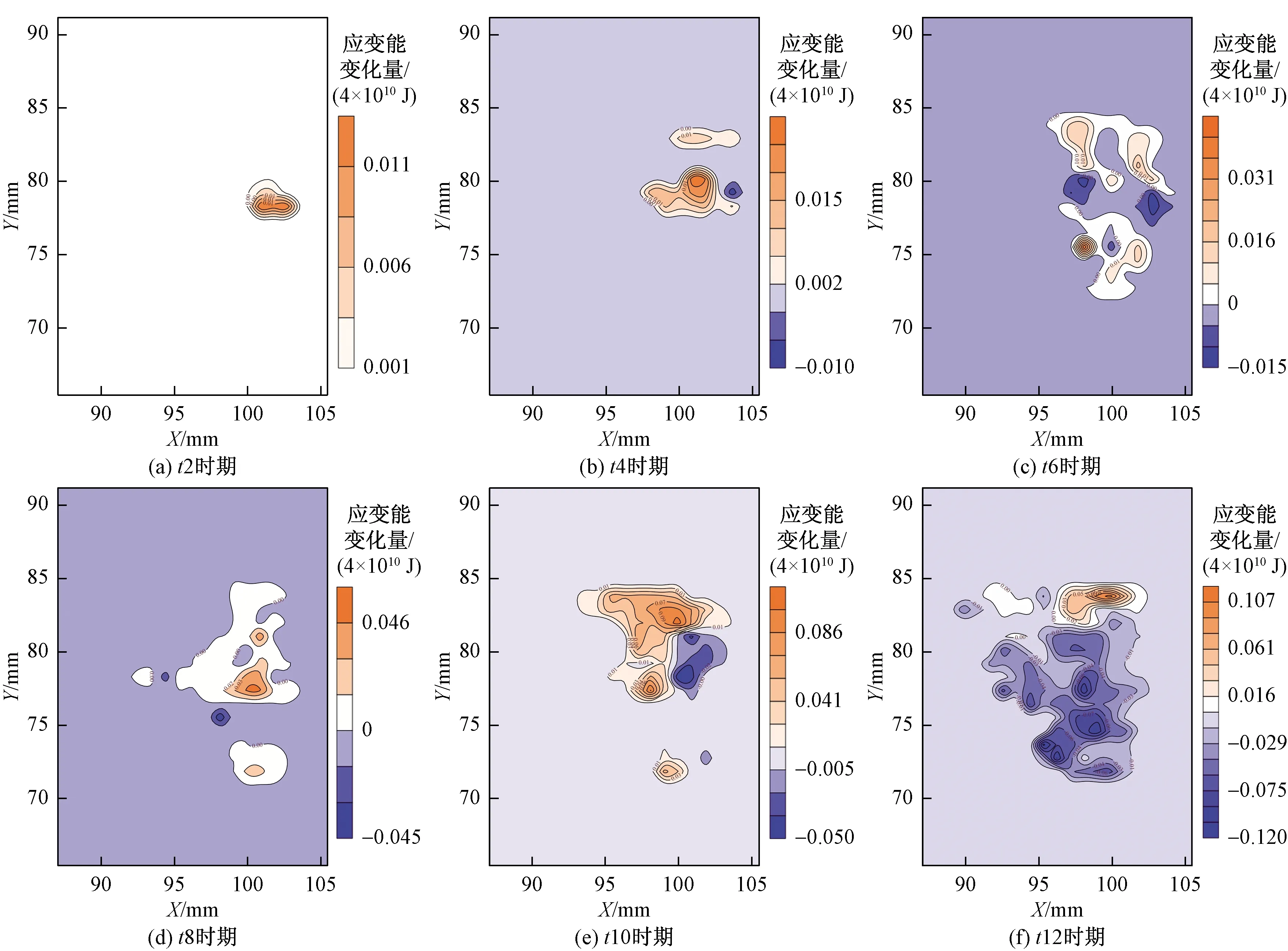
图13 正断层垂直剖面上的应变能密度变化图Fig.13 Variation diagram of strain energy density on vertical section of normal fault

应变能的积累和释放与断层形成在时间上具有一致性，应变能峰值其释放率决定了断裂规模。正断层形成后残余应变能以小规模的次级断裂、褶皱或阶梯状断层的形式逐渐释放，破裂主要在存储了高应变能的上盘局部区域产生。从能量的角度，地层应变能的积累和释放是形成断层的主要内因。

3.3 物理模拟实验的适用性讨论

实验为了降低情况复杂度，实验为抽象简化模拟，材料限制为脆性材料、层内均匀、无内部损伤、无应力集中破坏点，不考虑疲劳等因素。实验模型忽略了众多次要因素，对构造原型进行了大幅度抽象简化，忽略的次要因素对实验准确性的影响仍需进一步讨论。

实验模型未考虑重力作用，对于大规模的正断层，重力在地质时间下的横向作用对断层深部力学平衡具有很大影响，但对断层形成扩展的趋势和结果的影响仍不清楚[27-28]。重力在实验模型系统中仅表现为垂向作用和在弹性介质内产生侧向压力，无法模拟流体静压的影响。设想后续实验通过加载上覆均匀应力模拟地层重力作用，研究断层深部力学平衡对正断层形成扩展的趋势的影响能力。

虽然绝大多数正断层的演化变形过程是缓慢的，但是依旧存在重力、地震等高速作用下产生正断层的可能性。实验中拉伸速度为定值，尚不能认定正断层形成演化与加载速率无关。因此本文结论仅适用于可以用低速模拟的正断层。

4 结论

正断层面内主要发育高角度倾角；断层破碎带内断裂倾角和埋深呈指数函数关系；裂缝发育带断层倾角随埋深有“多期递减”现象，裂缝的发育程度不仅和距离断层的距离相关而且受到埋深的控制；损伤带内高角度和低角度倾角均为优势断层倾角。

砂层中上部最先出现明显断距；断距不断增大后断裂向砂层下部延展；断层下部断距、断裂程度明显大于上部；断层成核的起点在中上部断层段，下断层段的错动是由中上部断层段错动触发引起；纵向上断距并不均等，断距分布呈“双峰”特征。

正断层开始形成前，断层破碎带区域最早破裂，上盘次之，其后为下盘。应变能的释放时间决定了断裂产生时机，应变能释放率决定了断裂规模。正断层形成演化阶段可划分为断层初始期、断层孕育期、断层形成(Ⅰ、Ⅱ和Ⅲ)期、断层稳定期4个主要时期，不同时期的应变能密度峰值有1～3个数量级的差异。正断层形成后，残余了高应变能的上盘区域以多种形式逐渐释放应变能；从能量的角度，地层应变能的积累和释放是断层发育的主要内因。