船舶风载荷数值模拟中流域构造方法的研究与应用
2021-06-26于晨芳蒋武杰
张 亚,于晨芳,蒋武杰
(1. 江南造船(集团)有限责任公司,上海 201913;2. 中国船舶及海洋工程设计研究院,上海 200011)
0 引言
随着船舶能效设计指数(Energy Efficiency Design Index,EEDI)的逐步施行,特别是在国际海事组织(International Maritime Organization,简称:IMO)通过了《1973年国际防止船舶造成污染公约》附件6修正案之后,船东以及船舶设计单位对船舶性能的要求越来越高。集装箱船由于满载工况时上层建筑受风面积很大,风阻占总阻力比重偏大,很有必要针对箱船风载荷进行数值模拟研究。
目前风载荷的预报主要有风洞试验、经验公式和计算流体力学(computational fluid dynamics,简称:CFD)数值模拟3种方法。风洞试验是公认的精度最高的风载荷预报方法,但其周期长,价格昂贵,目前在新船的设计阶段应用率较低。从上世纪末开始,一些基于风洞试验数据的经验公式开始出现。BLENDERMANN根据一组系统的风洞数据,推导出船舶纵向力系数、横向力系数和艏摇力矩系数的计算公式。FUJIWARA通过逐步多元回归分析,提出一套计算船舶风载荷的计算公式。随着CFD数值模拟技术的发展和成熟,数值仿真方法开始应用于船舶风载荷预报。
在船舶风荷载数值模拟计算中,实际问题是,一般需要计算 180°范围内多个不同来流风向角工况,计算工况较多。通常情况下,针对每种风向角工况都需要建立相应的数值风洞模型,意味着对每一种工况都要进行计算域构造、网格离散、边界条件定义等重复性工作,导致工作量庞大,耗时费力。
本文基于STAR-CCM+平台,提出3种计算域构造方式,大幅减少重复性劳动,提高数值建模的效率,对实现船舶风载荷数值建模的完全流程化和自动化具有实用价值。
1 船模参数和数值方法
本文以15 000 TEU集装箱船为研究对象,主参数见表1。采用STAR-CCM+软件建立计算模型、划分网格并进行计算,计算船舶为实船尺度。
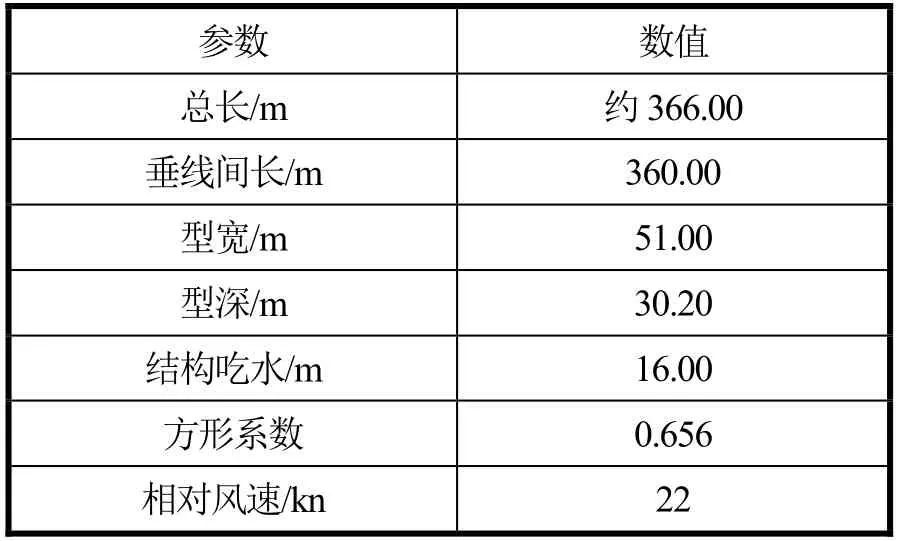
表1 船模参数
这3种流域构造方法数值模拟均采用定常计算,湍流模型选择Realizable K-Epsilon Two-Layer,壁面函数选用Two-Layer all y+ wall treatment model。
2 流域构造、网格划分及边界条件设置
2.1 移动参考系模型法(MRF)
移动参考系模型方法(Moving Reference Frame,简称:MRF)通常应用于计算域中存在旋转或者平移运动的情形,船舶多风向角风载荷计算,类似于绕船中的旋转运动,应用移动参考系模型可简化工作量。
船模长度为L
,宽度为B
,总高为H
,计算域为长方体,长度宽度方向均为9L
,高度方向为13H
,船模位于计算域正中心位置,如图1所示。经计算船舶侧投影方向阻塞比为0.85%,正投影方向阻塞比为0.12%,远低于工程要求的3%标准,边界对计算结果的影响很小。
图1 MRF计算域
MRF方法要求在船中创建笛卡尔坐标系,设定名称为ship,X
、Y
、Z
轴方向与基准坐标系相同。将随风向角变化的加密零部件和速度方向的坐标系指定为ship。不随风向角变化的物理量的坐标系指定为基准坐标系,如图2所示。
图2 MRF方法
网格化策略采用基于零部件的网格化(Part Based Meshing,简称:PBM)方法,在几何零部件上执行网格操作并生成流程。这种方法可允许对输入的零部件进行旋转,并通过生成流程将变化传输到体网格。因此,根据风向角变化对应旋转坐标系ship,即可输入不同角度的风,并自动适配网格划分方式,从而实现多风向角计算模型共享。
网格化模型的选择如表2所示。不同风向角下自动适配的网格分布见图3~图5。为了更好地捕捉围绕船体的流动特征,对局部地区(艏部、上建、烟囱、尾部、来流方向)进行加密。

表2 网格化模型

图3 40°风向角

图4 100°风向角

图5 160°风向角
从 0°~180°每隔 20°风向角计算一次。边界条件设置见表3。
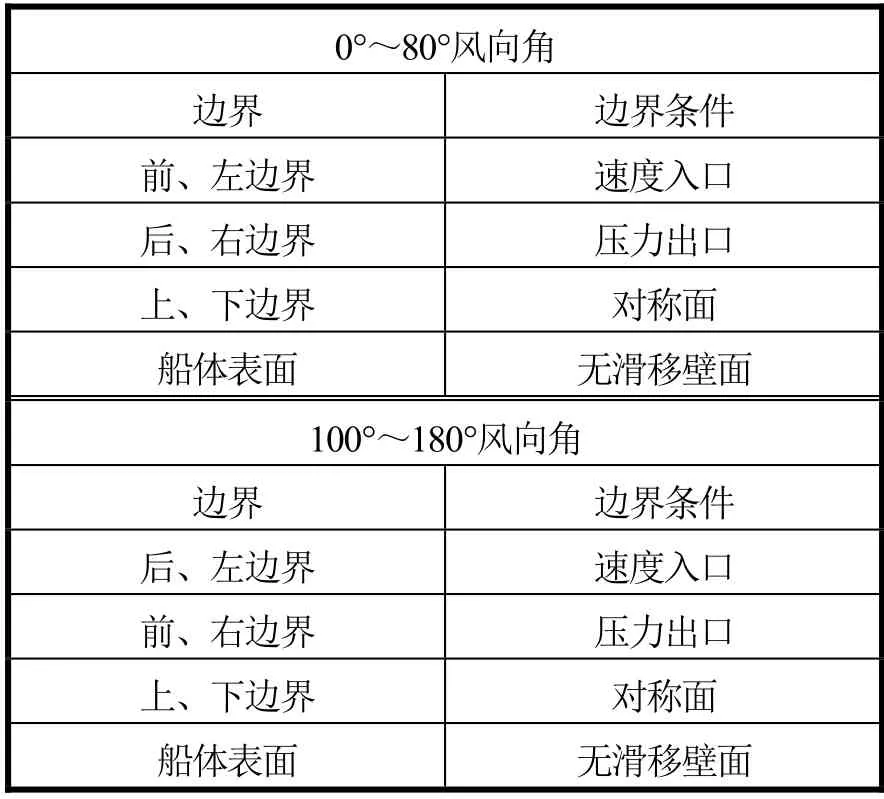
表3 MRF法边界条件设置
2.2 重叠网格法(Overset Mesh)
重叠网格法的计算域包含2个独立区域:背景区域(background)和重叠区域(overset)。两者通过重叠交界面进行求解的耦合。背景区域和重叠区域的相对位置关系见图5。背景区域的尺寸同MRF方法中计算域的尺寸相同,重叠区域船长方向为1.3L
,船宽方向为2B
,高度方向为2H
,见图6。
图5 Overset Mesh计算域
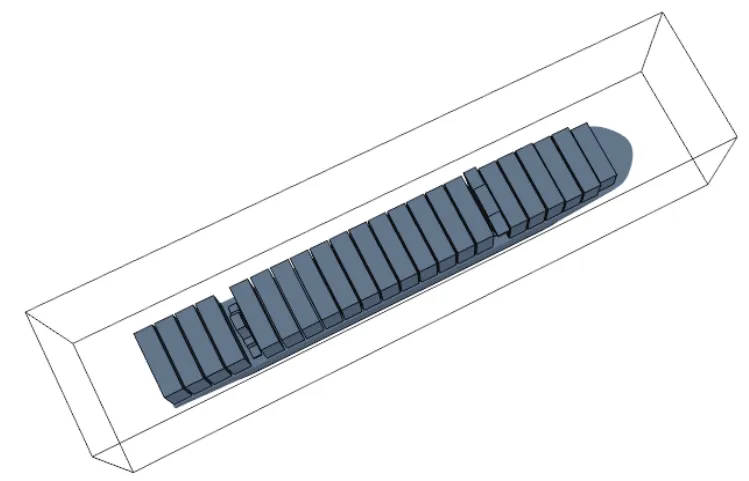
图6 重叠区域
为背景区域和重叠区域分别创建自动网格,网格化模型的选择参考MRF方法。背景区域和重叠区域自动网格的默认设置的更改保持一致,两者网格的不同的加密需求在自定义控制中进行体现。为在最大程度上消除在2个网格间插入变量时产生错误,2个区域在重叠交界面附近使用相近尺寸的网格。为实现多风向角计算模型共享,背景区域在重叠边界附近选用圆柱体形状体积控制,以保证重叠边界旋转之后,背景区域尺寸仍然与其相近。圆柱体体积控制生成网格见图7,重叠交界面附近的网格分布见图8。网格尺寸以及其他加密处理与MRF方法保持一致。

图7 圆柱体体积控制

图8 重叠网格
为能够在2个区域之间创建重叠交界面,将重叠网格类型分配给重叠区域中的至少1个边界。本计算中,将嵌入在背景区域内,且不是船身的一部分的所有表面,边界条件指定为重叠网格类型。背景区域的下边界与重叠区域的下边界共平面,两者指定相同的边界类型,即均为对称面。重叠交界面通过使用在一个网格上自动生成的接受者网络单元组和在另一个网格上生成的供应者网格单元组,对背景区域和重叠区域进行求解的耦合。供应者网格单元上的变量值通过插值来表示接受者网格单元上的变量值。本计算中插值方式设置为线型插值。边界条件设置见表4。

表4 重叠网格法边界条件设置
绕位于船中的局部坐标系,每隔 20°,重叠区域旋转1次,即可达到多风向角计算的目的。减少了网格划分、生成和边界条件设置的工作量,且保持了不同风向角下网格划分的一致性。
2.3 内外域分区构造法(Subregion)
将计算域分成内域(inner)和外域(outer),内外域交界面通过内部边界进行信息传递。
外域尺寸与MRF法中计算域尺寸相同,內域设置为圆柱体,见图9。

图9 Subregion计算域
圆柱体底面圆心位于船体底面中心,直径为2.2L
,高度为2H
。船模置于内域中,圆柱体形的內域能围绕其轴心做任意角度旋转,以实现多风向角工况的计算。网格其他加密处理参照MRF方法。创建1个自动网格,包含內域和外域,并针对所有零部件单独进行网格化。关于圆柱形交界面网格的处理,一个很好的做法是,让交界面每一侧的网格单元都互相垂直。为获得这一结果,从外域交界面和内域交界面2侧分别生成1个单棱柱层网格单元,便于展示,将棱柱层单元加密处理,网格情况见图10。网格尺寸以及其他加密处理与MRF方法保持一致。边界条件设置见表5。

图10 交界面单棱柱层网格

表5 Subregion边界条件设置
3 结果分析
在船舶研发阶段,船舶纵向力F
、横向力F
和艏摇力矩M
是关注的主要因素,相应的纵向力系数C
、横向力系数C
以及艏摇力矩系数C
的定义如下:
ρ
为空气密度,kg/m;V
为相对风速,m/s;L
为船舶总长,m;A
为船舶水上部分正面投影面积,m;A
为船舶水上部分侧向投影面积,m。船舶风载荷系数随风向角变化曲线见图11~图13。
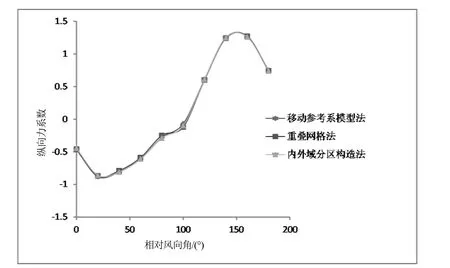
图11 纵向力系数随风向角变化曲线
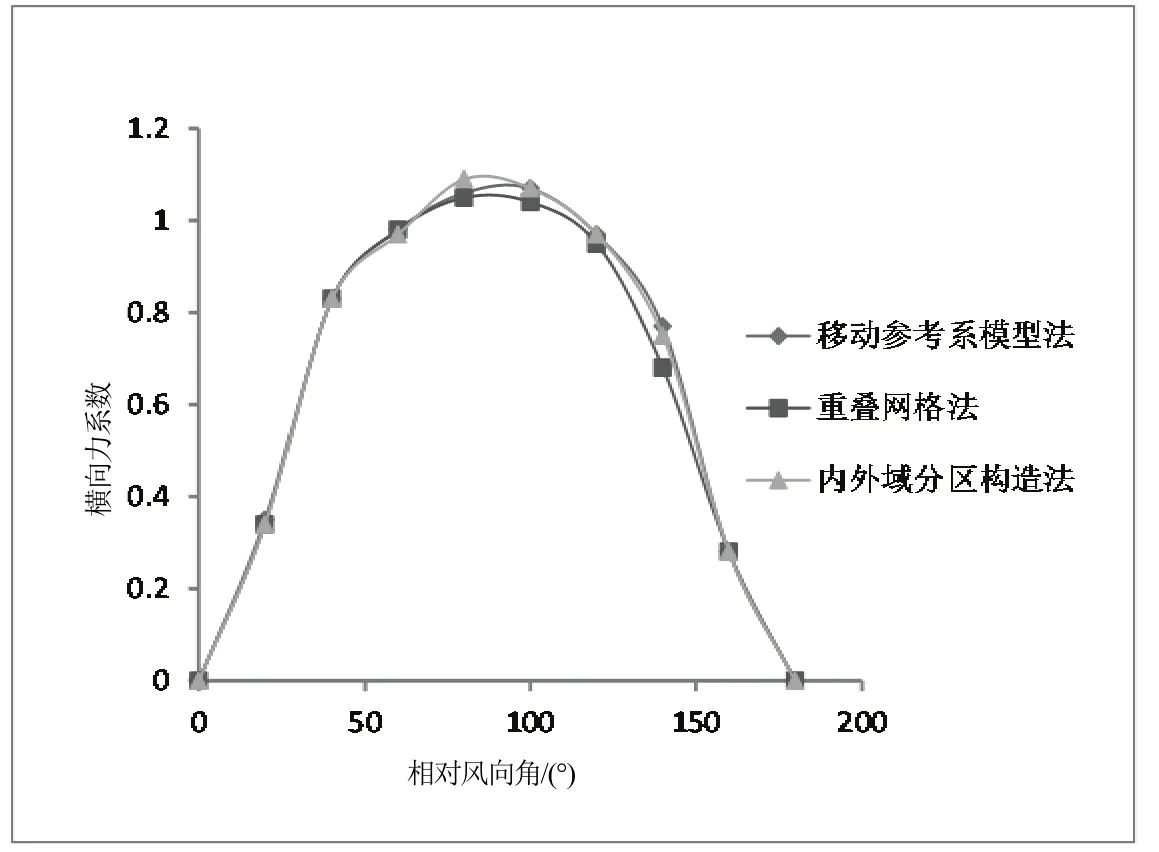
图12 横向力系数随风向角变化曲线

图13 艏摇力矩系数随风向角变化曲线
结果显示:3种流域构造方法的C
吻合非常好,C
和C
在部分点处略有差异,但差异不大,能够满足工程计算精度要求。原因可能是重叠网格法和内外域分区构造法在交界面处采用线性插值进行物理量的传输上,交界面位置和范围不同,对计算结果有微弱影响。而移动参考系模型法的流场连续,不需要设置交界面进行信息传递。4 经验公式
应用Fujiwara经验公式对正迎风时纵向力系数进行计算。

L
为船舶总长,m;B
为型宽,m;A
为甲板上层建筑侧投影面积,m;A
为水线以上迎风正投影面积,m;H
为从水线到AYV的垂向高度,m;其他参数取值可从ITTC 7.5-04-01中找到。数值模拟与经验公式的计算结果比较见表6。

表6 CFD与Fujiwara经验公式结果对比
从计算结果可以看出:3种流域构造方法计算得到的正迎风纵向力系数C
非常接近,且与Fujiwara经验公式结果相比,差异不大。由于集装箱船外流场流动形态复杂,经验公式计算结果具有一定的参考价值,但并不十分准确。因此,通过与Fujiwara经验公式结果的对比,初步证实数值模拟的准确性,还需后续风洞试验结果的进一步验证。
5 结论
基于STAR-CCM+平台,本文提出3种计算域构造方法,通过分析比较,得到以下结论:
1)移动参考系模型法(MRF)优势为计算域构造简单,不需要交界面进行信息传递;劣势为多风向角计算虽然不需重复进行网格划分,但坐标系移动之后,网格需重新生成。
2)重叠网格法(Overset Mesh)优势为可针对任意形状的重叠区域进行多风向角计算;劣势为重叠交界面上物理量的传递需要进行插值,计算结果可能受到微弱影响。
3)内外域分区构造法(Subregion)优势为易于理解;劣势为多风向角计算时,內域形状受限。
以15 000 TEU集装箱船为计算对象,比较分析船舶风载荷数值模拟结果,得到以下结论:
1)3种方法下纵向力系数C
、横向力系数C
、艏摇力矩系数C
的计算结果非常接近,流域构造的不同对计算结果的影响很小。原因可能是交界面处采用线性插值进行物理量的传输,交界面位置和范围不同,对计算结果有微弱影响。2)正迎风时纵向力系数与 Fujiwara经验公式相比,差异不大,初步证实计算结果的准确性,待后续风洞试验结果的进一步验证。
