多分支网络联合的倾斜影像仿射不变特征匹配

张传辉，姚国标，张 力，艾海滨，满孝成，黄鹏飞

1. 山东建筑大学测绘地理信息学院，山东 济南 250100； 2. 中国测绘科学研究院，北京 100830

随着智能测绘的落地生根，同步涌现出众多的非常规数据采集模式，如无人机倾斜航测及地面移动宽基线摄影等。非常规倾斜数据采集模式能够从不同角度获取目标场景影像，不仅为精细三维重建提供丰富的真实纹理信息，还具有良好的空间几何构形及重构精度优势。目前，三维重建技术已较为成熟，而如何从倾斜立体影像中自动和可靠地获取同名特征匹配，依然是当今数字摄影测量与计算机视觉领域共同研究的热难点问题。

针对存在较大变形的倾斜立体影像匹配问题，文献[1]提出多种有效的不变特征匹配算法。常用的仿射不变特征提取算法如Harris-Affine或Hessian-Affine等，主要运用二阶微分矩阵提取仿射不变区域特征，但由于特征检测与匹配的相对独立性，使得匹配的同名点难以实现位置上的精确对应。文献[2]提出由粗到精的多层次匹配策略，其中采用的最小二乘匹配(least square matching,LSM)算法使匹配点的定位精度提高到亚像素级，然而由于该方法在多级匹配过程中排除许多争议同名特征，导致大量影像冗余点未被充分利用。文献[3]对主流的仿射不变区域检测算法进行综合对比试验，表明了最大稳定极值区域(maximally stable extremal region,MSER)特征[4]对视角变化的立体影像适应性较好。此外，针对倾斜影像的ASIFT算法[5]，通过模拟离散的姿态角影像并使用SIFT算法[6]计算同名特征，通常能够获得大量的匹配点，然而该算法容易受相似纹理、阴影及视差不连续等因素影响，进而导致许多错误匹配。

深度学习作为一种深层次的特征表征方法，为解决倾斜影像匹配难题提供了一种全新的思路[7]。纵观现行的深度学习影像匹配算法，依据所得匹配点的稠密性可将其分为密集匹配和稀疏匹配两种类型。其中，深度学习密集匹配通过构建匹配代价网络模型，可端到端地计算视差图，继而实现影像重叠区域的逐像素密集匹配[8-9]，但限于目前的数据集规模，并且此类方法需要已知严格的核线关系，限制了其应用于倾斜影像匹配[10]。深度学习稀疏匹配意在利用深度学习策略实现高质量的特征提取和描述。其中，文献[11]将影像匹配各个阶段联合训练，取得了较优的结果，但该算法仍无法直接应用于复杂倾斜影像匹配，因其采用文献[12]的亮度不变特征，该特征难以适应影像间的仿射变形。此外，在特征描述学习阶段，该算法仅选择损失值较高的部分样本进行训练，虽节省了计算资源，却忽略其他样本的作用。而经典的L2-Net特征描述模型[13]，仅追求同名特征描述符间距离最小，当同名特征描述符间存在非同名特征描述符时，存在优化歧义，导致描述符的区分度较低。基于此，HardNet特征描述模型[14]运用顾及最近邻负样本的三元组网络结构，一定程度上增加了描述符的区分度，但仍缺少与其他近邻非同名特征描述符的距离约束，当大量相似样本参与优化时，仍难以训练出高质量描述符模型。

综上，面向具有复杂几何和辐射畸变的倾斜立体影像，无论经典不变特征匹配算法还是新型深度学习匹配网络，均难以得到较为可靠的匹配结果。其中，深度学习特征描述与匹配有望成为解决此类影像匹配的突破口，且目前鲜有仿射不变特征深度学习算法的报道。鉴于此，本文提出一种多分支卷积神经网络联合的倾斜立体影像仿射不变特征匹配算法。方法首先运用三分支网络(triplet network,TN)获得众多高质量仿射不变特征邻域；接着通过多重负样本采样策略构建多边约束损失函数，并训练多分支描述符网络(multi-branch descriptor network,MDN)，继而得到区分度较高的描述符；然后基于最/次近邻距离比率(nearest/next distance ratio,NNDR)测度获得同名特征，并进一步采用随机采样一致性(random sample consensus,RANSAC)算法剔除可能的误匹配点；最后多组倾斜影像匹配试验验证了本文算法的有效性。

1 本文方法

1.1 仿射不变特征提取

本文运用三分支卷积神经网络TN[15]学习影像邻域的仿射变换参数，进而结合Hessian初始特征邻域，变换形成仿射不变特征邻域(图1)。网络分支结构参数见表1。

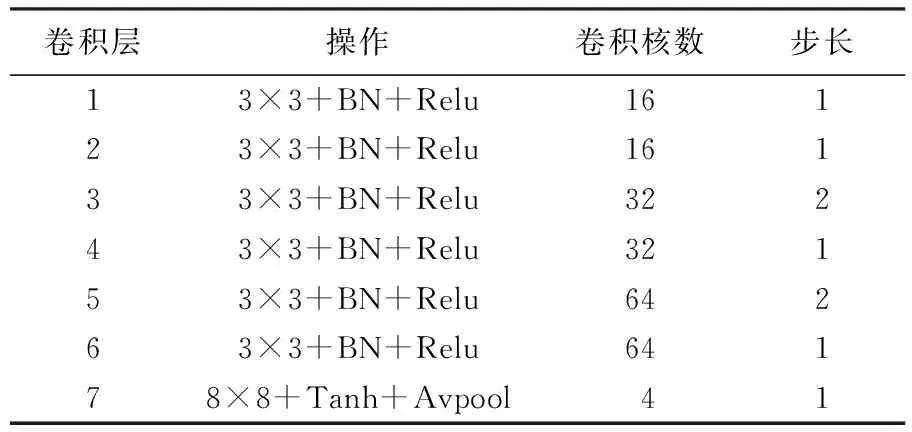
表1 TN分支结构参数

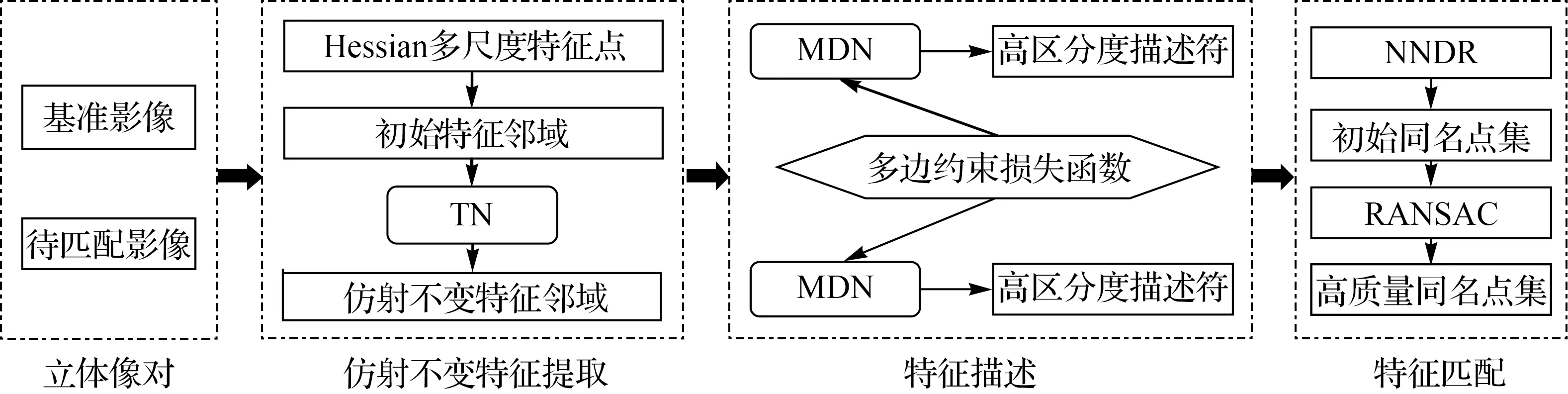
图1 本文算法流程Fig.1 The process of the proposed algorithm

TN由7层卷积层构成，每层卷积层包括3×3卷积、批量标准化(batch normalization,BN)[16]、线性修正单元(rectified linear unit,Relu)[17]等操作，其中最后一层采用8×8卷积、双正切函数(Tanh)、平均池化(average pooling,Avpool)等操作，输出仿射变换参数。另外，为进一步减少模型参数并使性能不变，使用步长为2的卷积层代替最大池化层[18]。TN的训练流程可简述如下。

(1) 在训练集中提取64×64像素大小的影像集，并进行一定范围内的随机仿射变换，得到影像集I，再以I中的同名点为中心剪裁得到32×32像素大小的影像块集。

(2) 将影像块集输入TN，得到仿射变换参数，继而构建仿射变换矩阵A，再利用公式I′=I·A-1对I中的影像块进行逆仿射变换，得到新影像块集I′。

(3) 运用描述符模型Hard-Net获得与I′对应的描述符，最后依据已知的描述符匹配关系和损失函数，经多次前向和反向传播，实现TN的训练。

不同于以往的训练方式[19]，本文将TN与特征描述网络串联，通过共用一套训练数据来完成TN的训练，因此显著地减少了制作训练集的工作量，是一种简单有效的多网络训练方式。此外，与ASIFT算法纠正整幅影像的仿射变形不同，本文方法提取若干特征影像块，并应用TN为每个特征影像块进行单独的纠正，有效地避免了若整幅影像不符合单一仿射变换模型而引起的匹配失效问题[20]。

1.2 特征描述

本文设计多分支描述符网络MDN对仿射不变特征邻域进行描述。其训练流程如图2所示。其中A、P表示同名影像块，其中心为同名像点；N1,N2,…,Nk表示A、P的非同名影像块。训练过程中，首先利用分支网络对影像块进行描述，得到描述符a、p、n1，n2，…，nk，其中a、p表示同名特征描述符；n1,n2，…，nk表示a、p的非同名特征描述符。然后运用采样策略选择多个ni并通过最小化损失函数来减小a、p间的距离，同时增大两者与多个ni的距离。最后基于迭代优化策略得到最优的模型参数。本文方法改进于文献[14]的三分支网络描述符模型，其损失函数如式(1)所示。

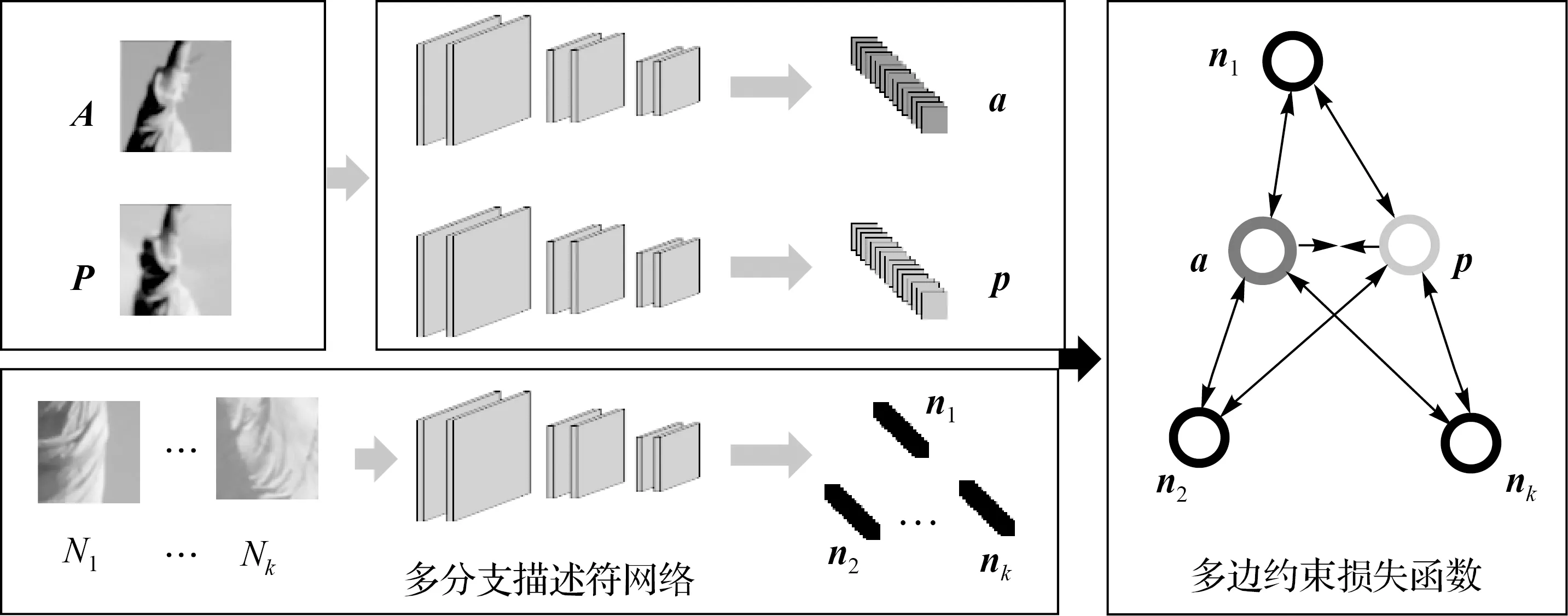
图2 MDN训练流程Fig.2 The process of MDN training

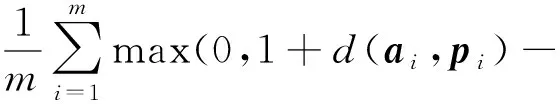
min(d(ai,naimin),d(npimin,pi)))

(1)

式中，m为批量大小；d()表示两描述符间的欧氏距离；naimin、npimin分别表示与ai、pi距离最近的非同名特征描述符。max()、min()分别表示取最大和最小值。

由式(1)可知，该损失函数仅将单一的非同名特征描述符纳入训练中，其训练的描述符模型难以区分影像中众多相似的特征区域。为解决此难题，本文提出多重负样本采样策略，选取多个近邻非同名特征描述符，并构建多边约束损失函数，进而训练多分支卷积神经网络模型MDN，以得到较高区分度的描述符。具体采样策略为：

(1) 运用文献[14]的分支网络对m对影像块进行描述，得到m对描述符，并计算彼此间欧氏距离，得到距离矩阵D，如式(2)所示

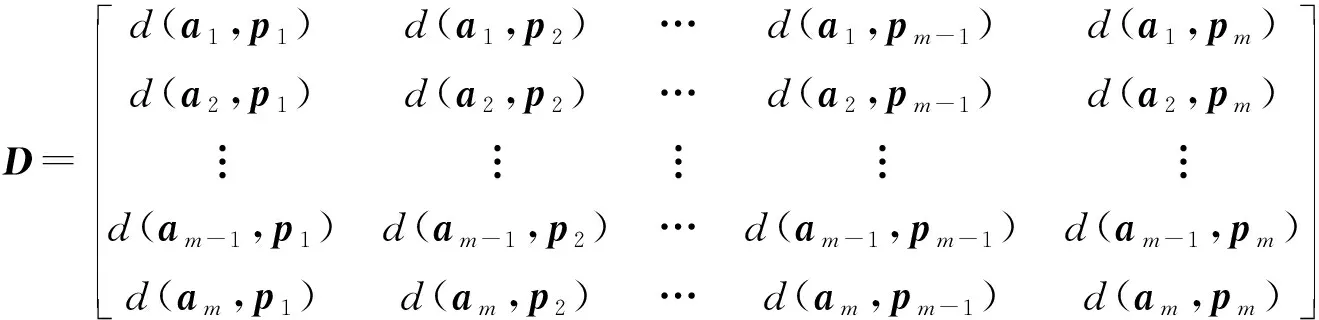
(2)

(2) 依据距离矩阵D，首先为a1选择与其最近的k个非同名特征描述符na1,1,na1,2,…,na1,k，并为p1进行同样选择，得到一组样本Sa1、Sp1如式(3)所示

(3)

(3) 利用步骤(2)得到全部样本。然后考虑单个近邻非同名特征描述符，建立单边损失函数，如式(4)所示

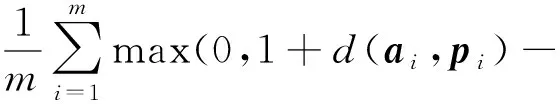
min(d(ai,nai,k),d(pi,npi,k)))

(4)

式中，Lk表示考虑第k近邻的非同名特征描述符所构成的损失函数；L1表示考虑最近的非同名特征描述符构成的损失函数，L2次之，以此类推。

(4) 考虑多个近邻距离，并为每个单边损失函数分配权重wk，且满足条件w1+w2+…+wk=1，得到多边约束损失函数，如式(5)所示

L=w1L1+w2L2+…+wkLk

(5)

(5) 通过多组w与k组合试验，选择k=3、w1=0.5、w2=0.3、w3=0.2结果最优，如式(6)所示

L=0.5L1+0.3L2+0.2L3

(6)

特征描述的关键在于增强同名特征的相似度和非同名特征的区分度，文献[14]在增强同名特征相似度的同时考虑了单一的非同名特征，一定程度上增加了与非同名特征的区分度，但面对相似特征较多的影像，该方法仍有改进的空间。本文通过建立多边约束损失函数，训练多分支描述符网络MDN，充分考虑了多个非同名描述符的作用，增强了模型对相似特征的区分能力。2.3节证明了以上论述。

1.3 特征匹配

完成仿射不变特征提取与描述模型的训练后，特征匹配过程可总结如下。

(1) 对立体像对使用Hessian算子提取初始特征邻域，并利用TN得到仿射变换参数，继而得到仿射不变特征邻域。运用MDN对仿射不变特征邻域进行描述，得到较高区分度的描述符。

(2) 对描述符采用NNDR测度(阈值为0.8)获得初始同名点集，并利用RANSAC算法在初始同名点集中随机选取最优n对(本文n取值为8)匹配点计算单应矩阵H，然后计算初始同名点投影误差，若误差小于3像素则输出内点集。经过多次迭代剔除可能的误匹配，获得最终匹配点集。

2 试验与分析

2.1 试验平台及数据

试验硬件平台配置为RTX2080ti GPU，i9-9900K处理器，64 GB内存；软件平台为Pycharm，使用Pytorch构建并训练神经网络。文中的两个模型均采用公开数据集Brown[21]训练，部分数据如图3所示。该数据集含有6个影像集，其中图3(a)、(d)是在同一类型数据中分别以DOG(difference of gaussian)特征点和Harris特征点为中心提取的，其他影像集来源相同。每个影像集包含超过40万对局部影像块样本，分辨率为64×64像素；标签数据为影像块索引及其匹配关系。采用数据增强方法，TN训练总数据量为一千万对影像块，批量大小为1024。采用随机梯度下降优化，动量为0.9，学习率为0.005，并在学习过程中逐渐下降。MDN训练总数据量为三千万对影像块，学习率为10，其余参数与TN相同。TN的训练时长为13 h左右；MDN为12 h左右。

如图3所示，用于模型训练的数据集属于多视多角度地面近景影像，包含大量的人造雕像和自然景观，为充分验证本文模型的匹配性能，选取4组不同区域类型的无人机倾斜影像为测试数据，如图4所示。对比图3和图4可见，训练数据与测试数据明显为不同数据源，测试数据不包含或极少包含训练数据中的地物类型，并且测试影像属于典型的匹配困难数据。测试影像详细描述见表2。

表2 测试影像描述

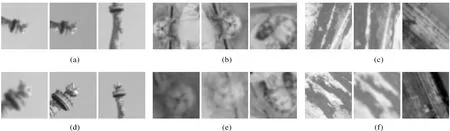
图3 部分Brown数据集Fig.3 Part of the Brown dataset

图4 测试影像Fig.4 Test images

2.2 试验评价指标

本文影像匹配试验采用的典型评价指标包括：①正确匹配点数nε0[22]，基于专业软件和人机交互的方式，选取15对均匀分布的像控点，计算得到单应矩阵，并将基准影像特征点投影至待匹配影像，与对应特征点计算误差ε0，若ε0<3像素，则视为正确匹配点。②匹配正确率p[23]，即正确匹配数与初始匹配数的百分比。③匹配误差εRMSE[24]，根据正确匹配点计算单应矩阵，然后手工选取15对检查点，计算均方根误差。④平均匹配时间t，对应算法在测试数据中匹配的平均耗时。

为进一步验证提出的描述符性能，采用文献[14]中的相关指标进行客观评价，具体为：

(1) 正样本间平均距离(average positive distance,APD)，即同名特征描述符相似性度量。APD值越小表示描述符匹配程度越好，如式(7)所示

(7)

(2) 正样本与负样本间最小平均距离(average positive and negative nearest distance,APNND)，即同名特征描述符与非同名特征描述符差异性度量。APNND越大表明描述符区分度越高，如式(8)所示

(8)

2.3 试验结果及分析

试验选取两种经典仿射不变特征匹配算法和一种深度学习匹配算法与本文算法进行对比：①MSER算法[4]，其能够提取目前公认最好的仿射不变区域；②ASIFT算法[5]，具有完全的仿射不变性；③SOS-Net算法[25]，使用三分支网络并在训练中引入正则项来提高描述符的稳健性。试验中，对传统算法提取到的仿射不变特征采用SIFT描述符进行描述，并利用NNDR测度和RANSAC算法得到最终匹配点集。SOS-Net算法则采用作者提供的预训练模型和相应的代码配置。各方法的匹配结果对比如图5—图9、表3所示。受篇幅限制，图5—图9仅展示上述算法中最优的ASIFT算法与本文算法的对比结果。

图5 UAV1-2立体影像匹配结果对比Fig.5 Comparison of matching results of UAV1-2 stereo images

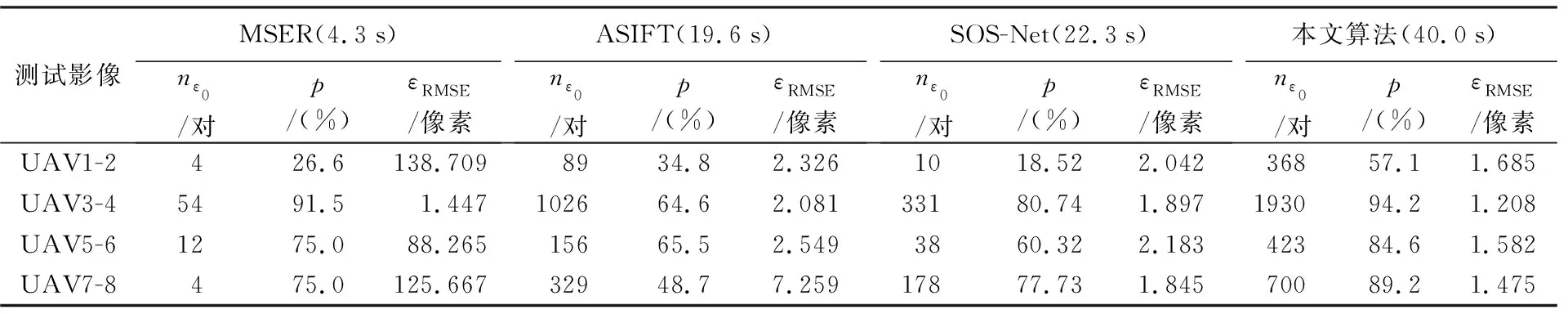
表3 不同算法匹配结果对比

图7 UAV5-6立体影像匹配结果对比Fig.7 Comparison of matching results of UAV5-6 stereo images

图8 UAV7-8立体影像匹配结果对比Fig.8 Comparison of matching results of UAV7-8 stereo images

图9 不同算法匹配结果对比Fig.9 Comparison of matching results of various algorithms

综合试验结果，分析如下：

(1) 本文算法在正确匹配数、匹配正确率、匹配误差方面具有显著优势，但匹配效率有待提升。本文算法在4组试验中分别得到368、1930、423、700对正确匹配点。MSER算法的正确匹配点数稀少且匹配误差较大，表明该算法在本文测试影像中几乎失效；ASIFT相较MSER算法匹配效果较好，但在测试影像中取得的正确匹配数目及精度仍不如本文方法。SOS-Net算法与本文算法存在一定差距，且在弱纹理和相似纹理影像中匹配数较少。在匹配正确率方面，本文算法在复杂倾斜影像中的效果均优于对比算法。本文算法的匹配误差为像素级，4组影像中匹配误差分别为1.685、1.208、1.582、1.475像素，对比其他方法具有显著优势。由于本文算法联合两个深度卷积网络进行不变特征的提取与描述，因此算法运行时间较长。

(2) 本文算法具有较好的适应性与可靠性。面向本文的测试影像，由于对应区域具有复杂几何和辐射畸变，并且纹理匮乏，经典算法难以提取有效的特征区域。而本文算法基于Hessian显著特征点，通过深度学习策略获得邻域间的仿射变换参数，可以得到数量充足的仿射不变特征邻域。在相似纹理区域，非同名特征间距离极小，使用传统SIFT描述符容易产生误匹配；而SOS-Net算法的描述符区分度较低；本文算法将多个距离最近的非同名特征描述符引入训练中，提高了模型对相似纹理特征的区分度，减少了误匹配。即使立体像对间存在较大倾角变化，本文算法也能够为每个局部特征邻域估算准确的仿射变换矩阵，较好顾及不同影像区域的仿射畸变差异，提取的仿射不变特征具有较高的重复率和稳定性。

为验证多边约束损失函数的有效性，设计描述符优化对比试验。随机产生7对距离相近的特征描述符，如图10(a)所示，同色圆表示同名特征描述符，不同色圆表示非同名特征描述符。试验采用Adam[26]优化器，分别使用文献[14]损失函数和本文损失函数对描述符进行150次迭代优化，如图10(b)和(c)所示。

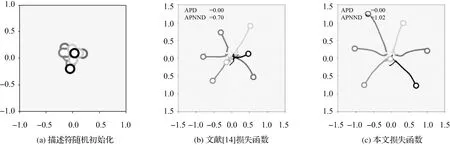
图10 不同损失函数下描述符优化结果对比Fig.10 Comparison of descriptor optimization results under different loss functions

结合2.2节评价指标分析图10可知，运用两损失函数对描述符进行优化后，APD值均为0，表明两者都能较好地减小同名特征描述符间的距离。但对比描述符的区分度，本文损失函数的APNND值为1.02，而文献[14]损失函数为0.70。表明前者能较好地将非同名特征描述符区分开，而后者的区分能力较弱。为充分验证本文损失函数性能，进行10组不同初始化的试验，并统计APNND值，如图11所示，表明本文的损失函数具有较好的区分度。

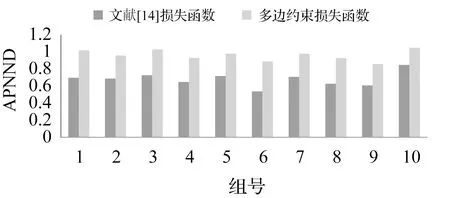
图11 不同损失函数下多组APNND值对比Fig.11 Comparison of APNND values of different losses in multiple experiments

为进一步验证算法在倾斜影像匹配中的效果，首先利用本文的仿射不变特征提取算法，基于测试影像，提取仿射不变特征邻域，然后分别使用文献[14]的损失函数和本文损失函数训练描述符模型，接着分别应用两种模型对仿射不变特征邻域进行描述，最后对描述符进行匹配。匹配结果对比如图12—图15和表4所示。

分析图12—图15和表4可知，相较文献[14]算法，本文算法的正确匹配数量、正确率和匹配精度均有一定提升。且相似纹理较多影像的匹配结果提升较大。原因在于多边约束损失函数训练的MDN提高了描述符的区分度，影像中的相似特征经过描述后，非同名特征描述符具有较大的欧氏距离，而同名特征描述符具有最小的欧氏距离，从而获得数量较多且正确率较高的同名特征。

图12 UAV1-2立体影像两描述符匹配结果对比Fig.12 Comparison of matching results of two descriptors of UAV1-2 stereo images

图13 UAV3-4立体影像两描述符匹配结果对比Fig.13 Comparison of matching results of two descriptors of UAV3-4 stereo images

图14 UAV5-6立体影像两描述符匹配结果对比Fig.14 Comparison of matching results of two descriptors of UAV5-6 stereo images

图15 UAV7-8立体影像两描述符匹配结果对比Fig.15 Comparison of matching results of two descriptors of UAV7-8 stereo images

表4 不同描述符匹配结果

3 结 论

本文提出的多分支卷积网络联合的仿射不变特征匹配算法，为倾斜影像匹配提供一种可行方法。算法运用三分支网络TN学习影像块仿射变换参数，以此提取仿射不变特征邻域，然后再利用提出的多边约束损失函数来训练多分支描述符网络MDN，该方法增强了描述符的区分度及其匹配效果，描述符优化试验及影像匹配试验均验证提出方法的有效性，并且本文算法在匹配数量、匹配正确率、匹配精度等方面具有显著优势。然而，由于特征检测与匹配的相对独立性，本文算法的匹配精度难以达到亚像素级，且由于神经网络的复杂性，算法的匹配效率受到一定限制。因此后续将研究设计一种轻量级、高效率网络，并运用最小二乘迭代匹配策略，实现仿射不变特征的快速提取与高质量匹配。