基于自适应遗传算法的电力仓库堆垛电机优化控制

贾广田，陈志炀，周 靖

（国网新源控股有限公司新安江水力发电厂，浙江 杭州 311600）

1 引言

随着电力企业生产规模的不断扩大，电力物资的多样性是对传统人工管理仓库的一个挑战[1]。越来越多的企业在仓库的现代化管理中采用了自动化仓库，简称AS/RS[3，4]。自动化仓储系统货物的存取是通过堆垛机完成的，因而其控制单元是整个控制系统的核心，为了实现高度自动化，满足操作的灵活性和实用性，达到人机交互的要求，堆垛机控制需要具备联机自动、单机自动以及手动3项功能。

（1）联机自动：常规状态下的工作方式。系统初始化后，堆垛机向监控系统索要货单；监控系统发送货单；接到货单的堆垛机在货单区域存入货单。

（2）单机自动：用于接收手动操作台，如入库、出库、伸、缩、升、降等动作命令。

（3）手动：与自动不同，手动仅能通过地面控制台触摸屏进行伸、缩、升、降、急停等操作，主要用于系统调试。当执行单条货单时，堆垛机自动到位，由人工通过地面控制台在触摸屏上操作货叉并取放货物。

堆垛机速度控制方式采用变频器对交流电动机进行调速控制，不仅可以实现异步电机的无极调速，还具有一定自我保护功能。变频器的调速范围广、输出平滑性好、机械特性硬，一方面，当电机带动较大负载启动时，可以实现电动机的软启动，减小冲击电流；另一方面，变频器能在电动机运行过程进行实时检测，比如电网电流瞬时下降、电网缺相、直流过电压、功率模块过热、电机短路等，并且立即采取措施，不仅保护了变频器，还保护了电机[5-7]。

变频器的变频原理可用式（1）表示：

式中：f为电源频率，p为电动机定子绕组的极对数，s为转差率。

由式（1）可得知，电源频率f与电机转速n成正比关系，所以当p与s为定值时，想要控制堆垛机在运行时的速度，可以通过改变电动机的频率f间接改变转子转速n，从而改变堆垛机的运行速度。

本文研究旨在堆垛机运行路径优化，基于某电力企业立体仓库，建立电机运行的优化模型，并引入改进的自适应遗传算法对优化模型进行求解，从而能有效提高运行效率。

2 自动化仓库堆垛机的路径优化

2.1 路径优化原理

智能小车把入库的货箱放到指定的入库台货架上，堆垛机从货架台取到货箱并送至仓库的货位上，堆垛机需要把货位上的货物送到出库台上，之后通过货物自动分拣系统分拣，再从分拣口将分拣后货箱通过汽车等运输工具运送到不同的分厂或车间，这就是AS/RS货架区工作的全过程，是一个典型的组合优化问题。

为了提高堆垛机从货架区中取货和存货的工作效率，需要选择一个最优化的路径。解决最优路径这一问题就等于解决了AS/RS工作效率问题，而这一问题的关键在于如何从多组路径中找到一组路径，这组路径是全部路径中的最优路径，它又称为组合优化。组合优化就是需要在数学结构中找到一个解，在满足约束条件下还能使目标函数达到最优。

2.2 堆垛机的作业方式

堆垛机的作业方式可分为单一作业方式和复合作业方式。

图1（左图）表示单一作业方式。当堆垛机接到一批出入库作业指令时，在此作业方式下，堆垛机每次都会先从原点出发执行入库作业指令，然后堆垛机回到原点；接着堆垛机再从原点出发来执行下一条入库作业指令，循环往复。由左图可知，每完成一项任务，则单一作业方式用时为tf=2tOP+2tOQ。式中，堆垛机在完成取送货物时，从O点运行到P点的拣选作业消耗时间为tOP，从O点运行到Q点的拣选作业消耗时间为tOQ。

图1（右图）表示复合作业方式。首先从原点出发执行入库作业，与单一作业方式不同的是，执行完入库作业后堆垛机直接执行新接受的出库作业指令，然后再运行到原点。复合作业的作业周期tf=tOP+tPQ+tOQ，式中tPQ表示堆垛机从P点运行到Q点的作业时间。

比较两种作业方式，显然复合作业方式比单一作业方式所用的时间短。然而此复合作业方式是以随机的顺序执行出入库作业，在高峰期这种方式的效率仍会给生产和客户需求带来不便，因而必须优化堆垛机运行总路径[8]。

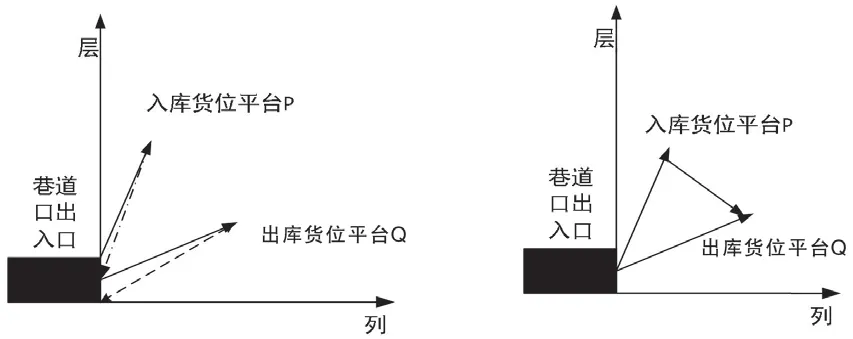
图1 拣选作业方式图

3 建立拣选作业路径优化模型

一般堆垛机采用复合作业工作模式，在这模式下，对于拣选出入库作业都是成对执行任务。根据tf=tOP+tPQ+tOQ可知，当一批出入库作业的货位确定时和也确定，而则随入库货位和出库货位执行顺序的改变而改变，因而只需考虑出入库货位配对方案对的影响。

结合实际情况，作出如下假设：

（1）一批作业中有m条入库作业和n条出库作业。

（2）堆垛机操作速度为恒速运行，最优路径规划时忽略存取时间。

（3）堆垛机水平和垂直运动时间相同，因而可以忽略启停时间。

（4）两点的用时取垂直或水平方向中最大值。

设P={P1，P2，L，Pm}，Q={Q1，Q2，L，Qm}为2个有序序列，其元素分别是依次执行的入库货位和出库货位，则堆垛机在拣选作业时通过复合作业工作模式路径为：

剩下n-m条单一拣选作业模式下出库作业。

综上，堆垛机复合作业路径优化目标为：让入库货位序列P不变，重新排序Q中的元素，并取出库货位序列Q中前m个元素与P中的元素依次配对顺序执行，从而使最小。

设第i个入库货位Pi的坐标为（xi，yi），令Q（i）表示重新排序后的第i个元素，其坐标为（xj，yj）。由此，建立复合作业方式路径优化模型为：

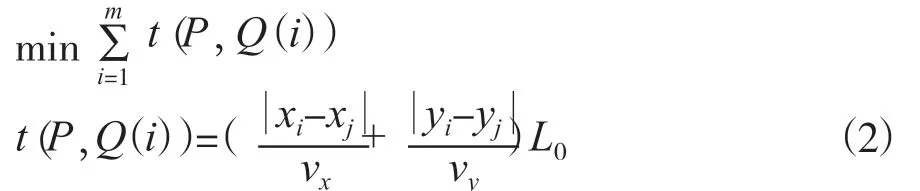
式（2）的约束条件为：

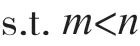
式中，vx为水平方向上堆垛机拣选作业时平均速度，vy为垂直方向上堆垛机拣选作业时平均速度，L0为货格的宽度。

改善GA（遗传算法）适应度函数为：

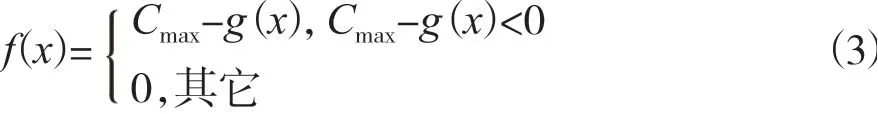
其中，Cmax可以取当前最大适值或者设定一个固定值；g（x）是问题的目标函数值；f（x）是个体的适应度。

目标函数g（x）为：

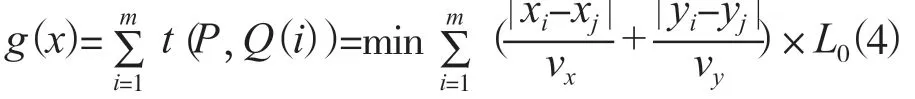
适应度函数f（x）为：

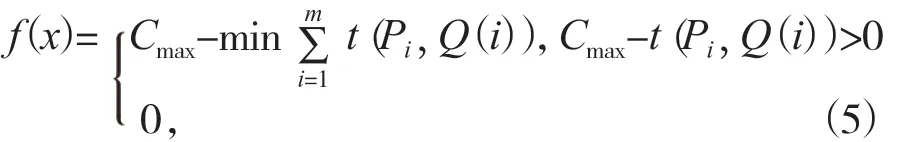
4 遗传算法的改善设计

4.1 基本的参数设定

本文研究对象设定为固定式货架，堆垛机在拣选作业过程中，在水平方向和垂直方向都是匀速运行，且只考虑堆垛机的拣选行走时间。设堆垛机在单排货架巷道内完成拣选作业，将点（0，0）作为巷道口，路径参数如表1所示。

表1 路径参数

4.2 自适应遗传算法原理

（1）GA

根据GA的遗传原理，在选择父代后，需要通过交叉概率Pc和Pm变异概率来产生下一代。因此，参数Pc和Pm直接影响算法的收敛性，因而成为影响GA优胜劣汰的关键。对于交叉概率Pc，当Pc的值越大时，相应的种群中父代被淘汰的可能性越大，子代产生的速度就越快；反之，当Pc的值较小时，又会延缓新个体的产生，甚至停滞不前。对于变异概率Pm，若Pm过小，不易形成子代；若Pm过大，则GA就成为了交叉概率中一定的随机搜索算法。在一般的GA中，Pc和Pm是固定的，针对不同的优化问题必须通过反复试验调整Pc和Pm以获得最优解，即使如此也难以保证获得最佳的参数值，因而运用GA处理路径优化问题时，其收敛速度较慢，算法不稳定性，甚至过早收敛于一个非全局最优解。

（2）AGA（自适应遗传算法）

近年来相关的研究人员作了大量的研究，其中被广泛接受的是Srinivas等提出的自适应遗传算法。AGA的核心思想是引入自适应调整函数，使遗传控制参数Pc和Pm随个体适应度大小和种群的分散程度自动调整[9]。当个体Pc和Pm取值不大时，即已经接近群体最佳适应度的时候，产生了性能较好的个体，可以尽量地保留住其优良模式，反之将对其采用较大的Pc和Pm，以加快个体的更新速度；当种群过早收敛，要陷入局部最优时，Pc和Pm需提高，反之当种群在解空间发散时，Pc和Pm需降低。通过这种自适应调整的Pc和Pm，在保持种群多样性的同时也保证了算法收敛性，提高了算法的优胜劣汰的能力。交叉概率Pc和变异概率Pm可用式（6）和式（7）表示：

式中，fmax为种群中最大适应度值，favg为每代种群平均适应度值，f'为较大父体的适应度值，f为两个父体的适应度值，k1,k2,k3,k4为自适应控制参数，一般取（0，1）区间的常数。

由式（6）和式（7）可以看出，对于适应度大于群体平均适应度的个体，其Pc和Pm的变化范围分别是（0，k1）和（0，k3）；对于适应度低于群体平均适应度的个体，其Pc和Pm分别是k2和k4；而对于每代种群中适应度最大的个体，其Pc和Pm均为零，从而确保当前代最优个体遗传至下一代。

AGA这种调整方式的优点体现在进化的后期。在进化的后期，最优个体已接近全局最优解，此时若再对其进行交叉、变异、产生的新个体适应度也不一定高。当然，这种调整在进化的初期会减缓新的优良个体的产生。为此，调整种群中最大适应度的个体Pc和Pm使其不等于零，这就等同于提高了最优个体的Pc和Pm，从而避免处于一种近似停滞的状态。对于每一代的优秀个体，可采用最优保存策略直接复制到下一代。

（3）参数的自适应调整

如前所述，GA的收敛特性的关键是Pc和Pm的选择，构造自适应调整函数的方法大同小异。本文采用AGA，Pc和Pm的自适应调整策略如式（8）和式（9）所示。此外，为了保留每一代的优良个体，可采用最优保存策略直接复制到下一代。

式中，fmax为种群中最大个体适应度值，favg为每代种群平均适应度值，f'为较大父体的适应度值，f为两个父体的适应度值，pc1=0.9，pc2=0.6，pm1=0.1，pm2=0.001。

5 仿真实验与结果分析

以AS/RS为例进行仿真实验，设置固定货架及堆垛机的参数：货架的长高都为1 m、堆垛机匀速运行、不计取货和放货时间；设定GA参数：种群规模pop=100，交叉概率pc=0.9，变异概率pm=0.05，最大允许进化代数为200代。随机生成拣选货位点，仿真实验结果和分析如下：

改善后的AGA与常规GA寻优作对比，对比如图2、图3所示。

图2 遗传算法进化曲线

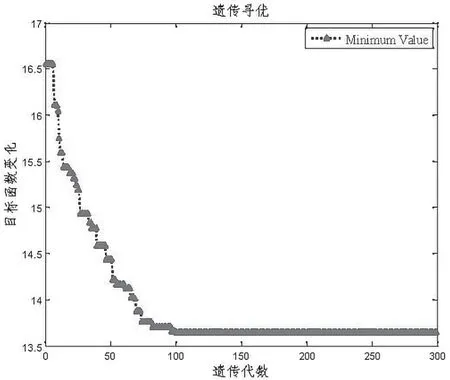
图3 自适应遗传算法进化曲线

AGA在求解拣选18个货位点的进化过程中，大约在迭代38次时已收敛，因而在解决拣选路径问题时，AGA比常规GA有更快的收敛速度，可以改善AS/RS的运行效率。

从表2中可以看出，经优化后的自适应遗传算法计算的运行路程平均降低20%左右，验证了自适应遗传算法的优越性。

表2 拣选作业运行路程

图4 遗传算法拣选路径

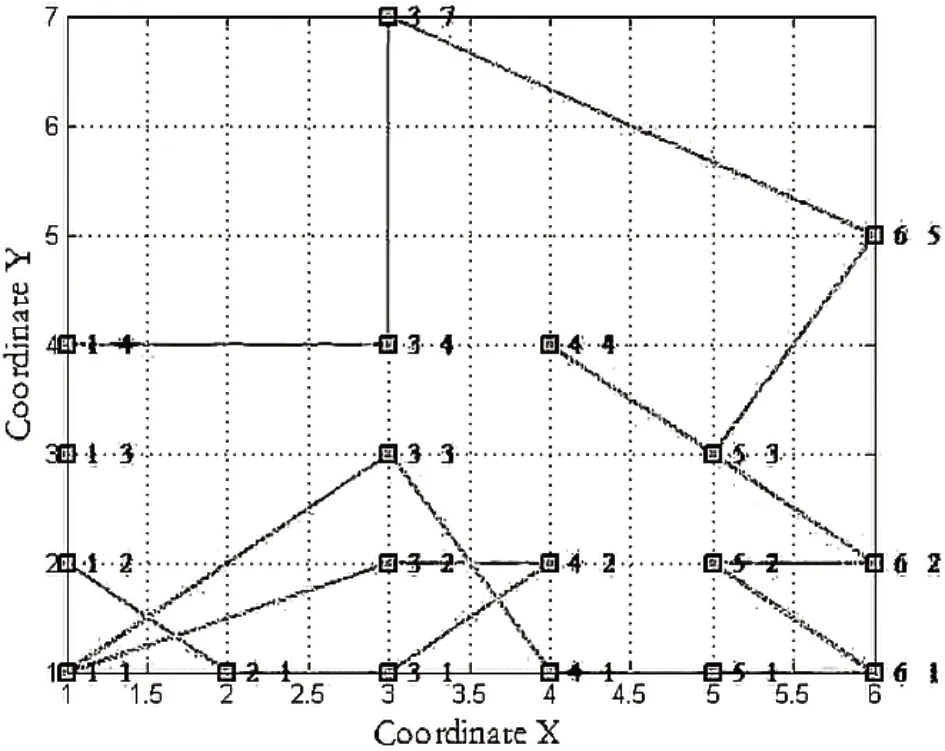
图5 改善后自适应遗传算法拣选路径

随机生成18个拣货点，采用GA和改善后的AGA分别对拣选货位点进行仿真实验，表2给出了其中5次这两种算法下的路径距离。图4表示GA实际运行的路径轨迹（0，0）→（1，2）→（2，1）→（3，1）→（4，2）→（5，1）→（6，1）→（5，3）→（6，2）→（5，2）→（4，1）→（3，2）→（3，3）→（4，4）→（6，5）→（3，7）→（1，4）→（1，3）→（3，4）→（0，0）。图5给出了改善后AGA算法的堆垛机运行的最短路径：（0,0）→（1,2）→（2,1）→（3,1）→（4,2）→（3,2）→（3,3）→（4,1）→（5,1）→（6,1）→（5,2）→（6,2）→（5,3）→（4,4）→（5,3)→（6,5）→（3,7）→（3,4）→（1,4）→（1,3）→→（0,0）。

改善后GA得到5次的最优结果均为52.74，而常规5次运算得到的拣选距离都大于60，显然不如改善后的AGA效果好，所以图5中AGA的拣选顺序要优于GA的拣选顺序。

6 结束语

针对物资仓库存在的诸多实际问题，基于某电力企业仓库实际情况，分析了实际中堆垛机在拣选作业时的速度与定位控制问题，给出了针对该固定货架模型拣选作业的特点。利用MATLAB软件进行编码和导入参数，证明改善后的AGA在解决拣选路径优化问题时，其收敛速度快于常规GA，收敛结果也优于常规GA。同时也验证了经过路径优化后的模型合理性，可以提高整个仓库的运行效率。