我国2019 年31 个行政区交通事故总量空间分析

谭立云

(华北科技学院理学院,河北 三河065201)

经查询2019 年我国国家统计局官网,我国2019 年31 个省、直辖市和自治区交通事故总数为247646 起,其中最多的省份是湖北高达23168 起,最低的省份是西藏,共468 起。为了对总体情况进行更好了解,我们利用Geoda 空间统计分析软件来进行空间探索和分析。

1 交通事故总量的箱形图分析

在Geoda 空间统计分析软件中,箱形图是一种特殊的四分位数地图,是在四分位地图基础上,再加上两个异常值,这种地图实际与“箱形”没任何联系,只是其构思是从箱线图演化而成,故称箱形图,它尤其强调具有异常值的地域单位。所谓异常值是指那些大于Q3+1.5d,或小于Q1-1.5d,其中d=Q3-Q1,称为四分位距,异常值又可以分为极端和温和两种:那些大于Q3+3d,或小于Q1-3d 的异常值称为极端异常值,而那些小于或等于Q3+3d,或大于或等于Q1-3d 的异常值称为温和异常值。在Geoda 中很容易做出箱形图,这里取温和异常值,见图1。

图1 交通事故箱线图分布图

从图1 可以看出,有一个高的温和异常值,这是湖北省,没有低温和异常值；交通事故低的省份(即小于Q1)集中在西藏、宁夏、甘肃、青海、湖南、海南、北京、上海等8 个地区；Q1和Q2之间的省份有新疆、内蒙古、东三省、重庆及河等7 个地区；Q2和Q3之间的省份有云南、山西、陕西、四川、天津、浙江、江苏、江西等8 个地区；大于Q3的省份有贵州、广西、广东、河南、山东、安徽和福建等7 个地区。交通事故总量表现出的聚集性非常明显。

在Geoda 空间统计分析软件中,很容易进行空间聚类,图2是聚为四类时的聚类图,从聚类图中可以看出这四类基本都是地理位置靠近且成片在一起的,这里的聚类图与线形图略有出入,地理位置特征更加明显。

图2 空间聚类(4 类)图

2 空间聚集性全局自相关莫兰指数分析

莫兰1950 年提出了全局自相关莫兰指数I,它是最早应用于检验空间关联性和集聚问题的指标,反映了整个研究区域内,各个地域单元与邻近地域单元之间的相似性,其计算公式为:

莫兰指数I 取值介于-1 与1 之间,大于0 表示正相关,值越大表明具有相似的属性集聚在一起(即高值与高值邻接、低值与低值邻接),小于0表示负相关,值越接近-1,表明具有相异的属性集聚在一起(即高值与低值邻接、低值与高值邻接),接近0,则表示属性是随机分布的,或者说不具有空间自相关性。

本案例中用GeoDa 计算得到全局自相关莫兰指数I=0.111＞0,表现出正相关,即表现出高指与高值邻接、低值与低值邻接。图3 表示的高值与高值邻接的行政区,图4 表现的是低值与低值邻接的行政区

图3 高值- 高值邻接的行政区示意图

图4 低值与低值邻接的行政区示意图

3 空间误差回归分析模型

以下考察GDP 与交通事故总量之间的回归关系,通过采取普通最小二乘回归、空间滞后回归和空间误差回归三种模型进行对比后发现,本模型最合适的模型是空间误差回归模型。

空间误差回归模型是如下的模型:

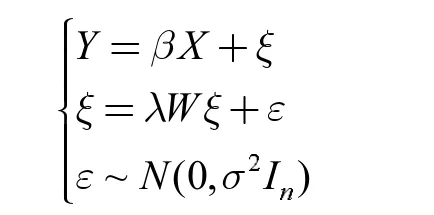
其中Y,X,W 分别表示GDP、交通事故总量、空间权重矩阵。空间权重我们这里取得按共边或共顶点及视为邻接,采取“后”方式计算权重矩阵。

最后得到的模型如表1(这里只展示回归系数,其他信息均删除)。

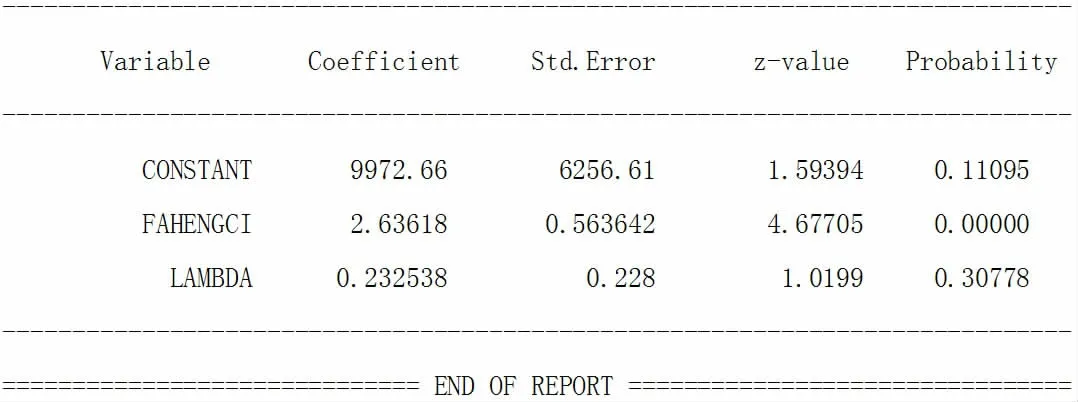
表1

即我们得到GDP 与交通事故总量的回归模型为:

GDP=9972.60+2.63628* 交通事故总数

但从模型检验结果可以看出来,参数λ 不显著,常数也不够显著,模型较为粗糙,GDP 与交通事故总量二者之间的正向关系我们可以理解,我们目前的经济发展在一定程度上还是粗放型,经济越发达的省份交通事故越多,从前面的箱形图、聚类图都可以印证这一点。

4 结论

通常数据都具有空间地理位置,因此我们在进行数据分析时,最理想的方法应该是采取利用空间数据分析方法。我们对2019 年我国31 个行政区的交通事故总量进行了分析,表现出较强的聚集性,即高值与高值邻接,低值与低值邻接。我们进一步对GDP与交通事故总数关系时发现,经济越发达的地区,交通事故总数越多,在发展经济时应该尊重人的生活,坚持人民至上、生命至上。