火炮身管指向测量中图像的特征提取与校正

齐寰宇,段修生,,马月辉，高旭端，张帅飞

(1.石家庄铁道大学，河北 石家庄 050043；2.河北省无人机侦测信息处理与运用技术重点实验室，河北 石家庄 050091)

基于点特征的单目位姿测量是利用多个控制点之间的约束，求解2个坐标系之间的位姿关系，一般称为PNP问题[1]。位姿测量精度受许多因素影响，如相机内参、特征点图像坐标、采集距离等，其中，特征点的中心提取是姿态解算的难点及关键点。针对火炮身管上特征点的提取，国内外学者提出了一系列的算法，但是常见的缺陷有：不适应野外复杂环境，提取精度差[2]；不适用于火炮的动态指向测量[3]。

针对火炮身管动态指向测量中存在的问题，笔者在动态测量火炮身管的基础上提出了一种基于自适应阈值下的多点校正和单点校正算法。对拍摄的图像网格化搜索最佳变换参数，以适应不同的光照，提取角点后通过特征点之间的几何约束关系优化提取结果，优化的结果可直接用于火炮身管姿态测量的计算中。经实验表明：特征点提取的校正算法对提高测量精度取得了良好的效果。

1 条状标志物特征

运用高分辨率的摄像机实时采集火炮身管上的标志物图像，通过机器视觉的方法获取标志物的运动参数进而得到火炮身管的姿态(高低角、方位角)。因此，标志物在测量过程中扮演着重要的角色，设计时需要考虑标志物的尺寸、特征点个数、特征标识的选择以及特征点之间的几何约束关系等对测量精度的影响。

为适应实弹射击考核环境及火炮自身特点，对标志物的面积、质量等均采取限制措施。另外，考虑到图像采集过程中可能存在烟雾遮挡、检测丢失等情况，因此需要具有冗余的特征点个数保证能够进行姿态解算。如图1所示，采用背景是白色，含多个同直线、等间距、黑白相间的标志圆的条状标志物作为可粘贴于火炮身管正面上的合作靶标。

将圆心作为待提取的特征点，约定其世界坐标为已知，记为Pi=(Xi,Yi,Zi)T，则

(1)

式中：d为相邻圆心间距；nnum为圆的序号。

根据投影成像原理，像元尺寸、焦距、采集距离和单个像素在物理空间的尺寸关系示意图如图2所示。

由相似三角形计算可得

(2)

式中：D为Ox对应的采集距离；L为单个像素对应的世界空间尺寸；f为焦距；l为像元尺寸。则物理空间下标志圆半径R与图像平面下特征圆半径r关系如下：

(3)

因此，可通过式(2)、(3)大致获得图像中标志圆的半径。

设在图像坐标系下，圆心坐标为(ox，oy)，半径为r的标志圆的方程为

(xi-ox)2+(yi-oy)2=r2,

(4)

式中，i=1，2，…，n.

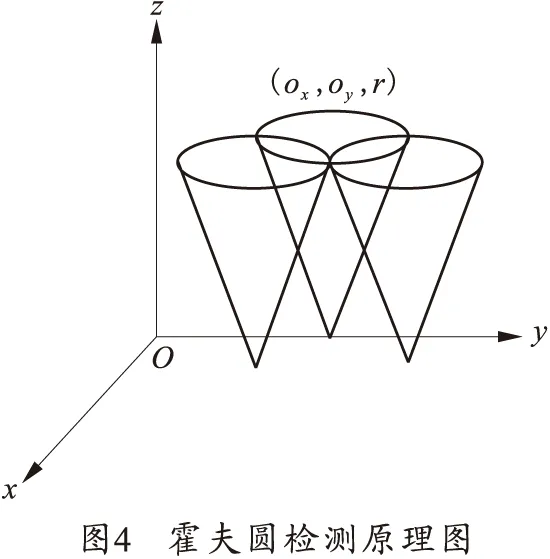
在图像坐标系中标志圆边界上的一点(xi，yi)对应式(4)中一个三维锥面，故所检测的圆边界上的点对应的三维锥面如图3所示，由此可得出霍夫圆的圆心坐标及半径。

在利用霍夫变换检测圆的算法中，需在参数空间建立一个累加三维数组D(ox,oy,r),其中r为变量，设定阈值δ，在阈值范围内变化r的绝对值，如图4所示。对图像中每一个圆边界点计算(ox,oy,r)，并对数组D(ox,oy,r)进行累加，检测完后，数组D(ox,oy,r)中的最大值所对应的(ox,oy)为圆心坐标，r为半径。

检测出条状物中标志圆的大致位置后，从左至右依次记录下圆的序号、半径r、圆心坐标等初始参数。根据相关参数尽可能只保留条状物对原图进行切割，以此减小拍摄背景对特征检测造成的影响，提高运算效率。

2 角点提取算法

2.1 Harris角点检测算法

在求取图像感兴趣区中黑白交叉的圆心处坐标时，需要寻找X形角点，主要运用Harris角点检测的思想。计算公式为

(5)

式中：Ix为图像I在x方向的灰度梯度；Iy为y方向的灰度梯度[4-5]。

角点响应函数CRF定义为

CRF=det(M)-k×trace2(M)，

(6)

式中：det为矩阵M的行列式；trace为矩阵对角线元素的和；k为默认常数，k=0.04.

若矩阵M在一个像素点上的两个特征值很大，则在该点向任意方向上的一个很小的移动都会引起灰度值的较大变化，当CRF取得局部极大值，则所在的点作为角点[6]。

在图像采集中，难免受到光照、仪器、尘雾等各方面的干扰，导致图像存在噪点,质量受到影响。在此次设计中，利用高斯滤波器对所采集图像数据进行平滑预处理，同时，能够更多地保留图像的总体灰度分布特征[7]。因此，矩阵M重新定义为

(7)

式中，G为高斯模板。

Harris算子优势显著，但是存在两方面局限性：一是对图像尺度十分敏感，不具有尺度不变性；二是所提取的角点是像素级，常常受到相机分辨率的限制。当火炮周边光线较暗造成标志物黑白区别不明显时，会出现角点未检测的情况；当火炮处于光线强烈的环境时，会使标志物某区域曝光过度，会出现黑白边界过度分离使得标志物中心分离出两个角点或者角点落在黑白格的边界上而不在十字交点上的现象。尤其在野外测试中，会经常出现上述情况。因此，不能直接将处理结果应用到实际的火炮身管姿态测量的解算中，需对此提取结果进行深入的校正优化处理。

2.2 角点校正算法

2.2.1 多点校正

多点校正利用各个标志圆中圆心在同一条直线上的约束，采用最小二乘法对所检测出圆心角点坐标进行直线拟合，设拟合直线上x和y之间的函数关系为

y=ax+b，

(8)

式中，a、b均为待定参数。

对于等精度测量所得到的n组数据(xi,yi),i=1,2,…，n,xi值被认为是准确的，所有的误差只联系着yi，在估计参数时，要求观测值yi的偏差的加权平方和最小，因此应有

(9)

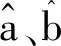
(10)

(11)

2.2.2 单点校正

Harris算法通过微分运算和自相关矩阵来提取图像中的角点[8]，分别计算出图像在x、y方向上的梯度自相关函数相联系的矩阵M及自相关函数的一阶曲率，当两个曲率值都很高时，则将此点作为角点。在现实中标志物中圆心处的面积并非一个像素单位，而是一个灰度值由大逐渐变小直至恒定的阴影面积，因此，圆心处噪音较大，在角点检测过程中，目标像素点(x、y)在x、y方向尚未移动到真实圆心处，即检测到角点，即使经过直线拟合校正后误差依然较大。

针对上述问题，首先选择指数变换的方法，将切割后图像狭窄的靠近黑色部分像素值映射到更宽的像素值范围，便于角点搜索：

S=C×Rλ,

(12)

式中：S为增强后图像；R为滤波后的感兴趣区图像；λ为指数参数；C为常数。设定λ的阈值范围与步长，经过网格化搜索，利用解算值与倾角仪测量值作比较，经多幅图像实验，得出最优解。

指数增强后选择标志圆轮廓左、右处的噪音较小的“┤”形和“├”形角点作为运算角点，利用两个运算角点与圆心角点的几何关系求出圆心角点坐标。

利用拟合直线校正后的圆心角点(xi,yi)，将其沿着拟合直线上分别向左、向右移动n个像素，作为左、右标志点，设左标志点坐标为(xflag,yflag)其计算公式如下：

(13)

(xi-xflag)2+(yi-yflag)2=r2,

(14)

式中，(xi,yi)为拟合直线校正后的圆心角点。由此两个标志点设置阈值范围，筛选出标志圆轮廓边缘的“┤”形和“├”形角点，设单个圆轮廓的左、右角点分别为(xleft,yleft),(xright,yright)，校正后的圆心角点为(xend,yend)，则

(15)

(16)

将校正后的蓝色圆心角点与校正前的绿色角点在图中对比，效果如图5所示。图中红色圆形、蓝色圆形分别为经霍夫算法检测到的标志圆轮廓及序号识别圆轮廓。从图5中可以直观看出偏离实际圆心的角点经校正后明显回归正常。

3 基于条状标志物的指向解算

如图6所示，建立3个坐标参考系，模拟条状标志物在理想针孔成像模型下的成像过程，图中OC-xcyczc为相机坐标系，z轴与镜头光轴重合。Op-xpyp为图像坐标系，坐标的单位长度为一个像素值[9]。Ob-xbybzb是以条状标志物所在的平面为xOy面的世界坐标系，条状标志物位于火炮身管之上，因此火炮身管的姿态角也与该坐标系的位姿一一对应[10]。在火炮身管旋转过程中，始终以火炮所在直线作为世界坐标系的z轴。

在不考虑镜头畸变的情况下，标志物上任一角点P在世界坐标系下的齐次坐标向量Pb与其投影点P′在图像坐标系下的齐次坐标向量P满足关系：

(17)

式中:zb=0；M1为相机内参矩阵，包括焦距、偏移参数和镜头畸变参数，可利用多幅图像进行相机标定得出；M2为外参矩阵由旋转矩阵R和平移向量t构成，在火炮身管旋转时，不同的位置对应不同的外参矩阵，且定义某一时刻图像的单应性矩阵H=[h1h2h3]，则

P=HPb,

(18)

H=[h1h2h3]=ηM1[r1r2t].

(19)

根据每一幅图像得到的所有角点及其投影的坐标可以求解出单应性矩阵[11]。令μ=1/η，分解式(19)得到：

(20)

在进行正式测量之前，先对火炮身管进行校零，然后采集零位置图像，计算出零位置旋转矩阵R0，随着身管的运动采集对应图像并计算出与之对应的旋转矩阵Rn,则可以得到身管从零位置到某时刻位置n的旋转矩阵：

(21)

根据身管的运动模型以及标志物与之的相对位置，可以得到高低角α、方位角β与旋转矩阵Tn之间的关系，解出这两个角度。

4 实验验证

实验中采用摄影摇臂三脚架模拟火炮身管，将条状标志物固定在摇臂上，同时摇臂上安装倾角仪，用于确定摇臂相对于零位置的姿态角，以此为参考值，验证测量精度。选用海康威视工业相机(分辨率为2 448×2 048)和PENTAX H1214-M镜头，实验系统如图7所示。

在处理之前，打开摇臂，倾角仪设为常开状态，将摇臂做两个自由度的旋转，采集图像的同时记录下倾角仪的度数。设定指数的变化范围及步长，解算不同参数下的不同姿态结果，与倾角仪的读数相比较，搜索最佳指数参数，流程图如图8所示。

在得到最优预处理参数后，采集图像，利用特征提取、校正算法及指向解算的原理，解算出火炮的姿态角，实验数据如表1所示。

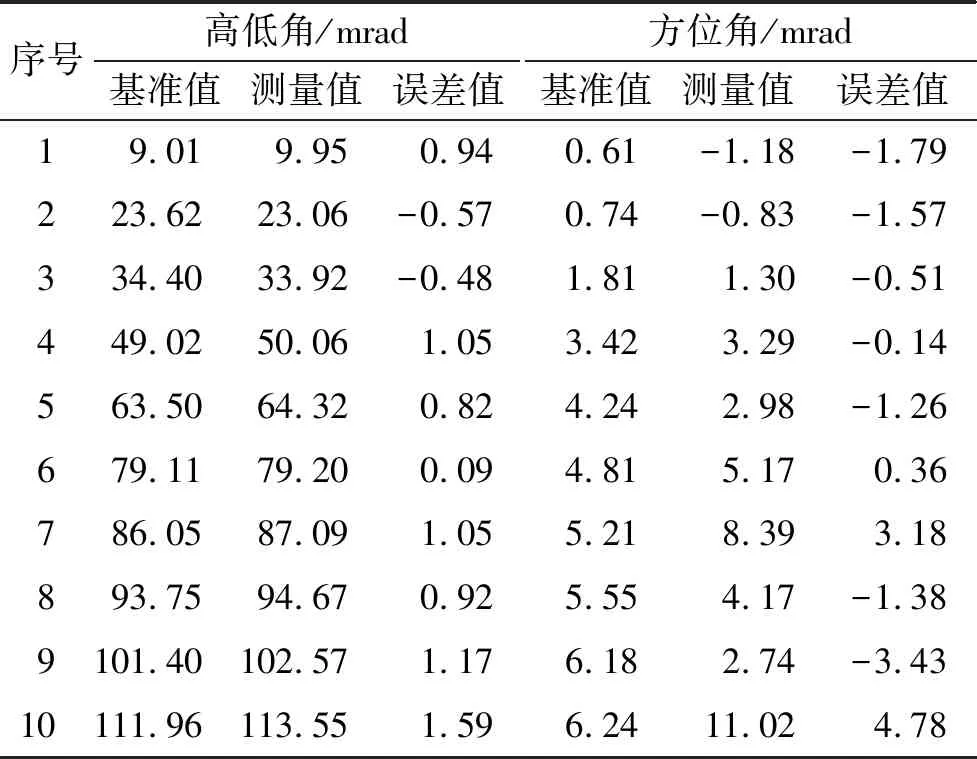
表1 实验测量结果

结果显示，经两次校正后角点所计算的身管高低角与倾角仪的度数基本吻合，高低误差在2.1 mrad以内，由实验数据可观测到：随着方位角的不断增加，高低角与方位角测量误差也随之增加，在建立高低角测量误差模型时，根据独立随机误差性质及误差传播理论得到误差系数：

(24)

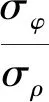
可以看出，误差系数近似为方位角余弦函数的倒数，且与采集距离、特征点间隔、相机分辨率均有关系；由于摄像机模型的自身限制，对沿光轴信息获取不敏感，导致方位角测量误差较大。因此，在下一步研究中，将重点研究双目图像处理及特征点合理分布、身管曲率问题，提高测量精度。

5 结束语

根据复杂环境下火炮身管指向测量的特点，提出了应用于身管运动情况下的特征提取与校正的方法，实验证明，该方法与现有身管指向测量技术相比较，最大改进在于能够自适应野外环境下的动态测量，且测量精度满足要求，成本大大下降，促进了非接触式位姿测量技术的发展，为部队的军事训练考核、射击精度的评估找到了一个新的解决方案。在下一步的工作中，可以通过改善硬件条件或增加双目相机，优化算法，进一步提升方位角的测量精度。