基于改进型灰色-马尔可夫预测模型的装备损耗研究
2021-06-25李籽圻陈桂明许令亮李乔扬
李籽圻,陈桂明,许令亮,李乔扬
(1.火箭军工程大学 研究生院,陕西 西安 710025;2.火箭军工程大学 作战保障学院,陕西 西安 710025)
现代技术特别是高新技术发展迅猛,作战形式逐步转变为海、陆、空、天、电(磁)多维一体,战场环境瞬息万变。先进装备作为未来作战的核心力量,对打击敌方重要目标和战局的扭转等起着关键性作用。因此,在战争开始前,大型重要装备的储备与保障问题必须慎重考虑,作为重点进行深入研究。
随着战斗的深入,武器装备的损耗影响着战争的成败。由于影响战争的因素错综复杂、盘根交错,对战时装备损耗模型的建立及预测分析而言,变得更加复杂和困难。
建立较为准确的战时装备损耗预测模型,对于装备的储备与保障起到关键性作用,有利于决策者做出科学合理的判断。国内外学者也加大对装备损耗的预测研究分析,文献[1]运用随机过程理论,建立了描述军用装备战损的数学模型,并导出了平均损耗速率的计算公式进行预测分析。文献[2]运用平稳时间序列模型,建立了武器装备损耗备件预测模型。文献[3]利用模糊神经网络算法,进行了装备损耗预测方法应用研究。文献[4]以最大综合战斗力指数为目标函数,考虑多种预测影响因素,建立多约束条件下的数学模型,并运用遗传算法对模型进行求解,但影响战场环境因素众多,所建立的模型较复杂,求解较困难。文献[5]通过引入火力分配系数矩阵,改进兰彻斯特战斗方程,结合武器毁伤系数,建立了空空导弹消耗量预测模型。文献[6]研究了基于遗传算法的空空导弹消耗量BP神经网络预测方法。文献[7]提出综合毁伤率概念并给出算法,基于最小弹药消耗量和最优活力分配原则,利用加权平均的思想,建立计算模型,为弹药预测建立基础,但是对于不同目标之间的权重配比,缺乏一定的理论分析。
传统的预测方法,大多基于数据的拟合或统计学的知识。但对于战时装备损耗,随着战斗进程的推进,各数据之间差异较大,十分分散,规律性不强,导致预测精度较低。利用智能算法进行预测,需要大量的数据集训练模型,而战时装备损耗的数据较少,并且过多的训练次数,会使模型记忆训练数据脱离原有数据之间的关系,出现过拟合现象,导致模型泛化能力比较差。
1 整体框架
针对战时装备损耗的特点,笔者提出改进型灰色-马尔可夫模型。灰色理论由邓聚龙教授在1982年首次提出,至今灰色理论已经形成了一套完整的分析、预测、评估等系统体系,是一种适合信息不完备系统建模的方法[8]。灰色GM(1,1)预测模型首先将原始数据处理成单增趋势的新数据,满足灰色理论的级比,就可以运用灰色理论。灰色理论在处理小样本、残缺信息等有着独特的优势,但是预测精度较低[9-11]。马尔可夫过程是指,将来的事件状态取决于当前事件状态,与过去事件状态无关,具有无后效性。战时装备损耗的特点满足这一条件,将来所需的预测值,只与当前时刻状态有关,而与过去状态无关[12]。因此,结合马尔可夫预测理论,使预测信息更加精确,有利于决策者做出判断。装备损耗数据受战场环境影响较大,无法明确的区分出各个因素对装备损耗数据的影响,而模糊C均值聚类分析适用于处理数据之间的模糊关系,深层次地分析数据之间的相似程度,并对其进行分类[13-15]。
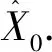
图1为笔者提出的改进型灰色-马尔可夫预测模型的方法流程图。
2 改进型灰色-马尔科夫预测模型
2.1 数据处理
设原始数据X0={x0(1),x0(2),…,x0(n)},xmax代表原始数据中的最大值,xmin代表原始数据中的最小值,P表示两者之比,即:
xmax=max{X0},
(1)
xmin=min{X0} ,
(2)
P=xmax/xmin.
(3)
对原始数据进行加速指数变换:
X1={x1(1),x1(2),…,x1(n)} ,
(4)
式中,
x1(k)=x0(k)×Pk-1,k=1,2,…,n.
(5)
再进行几何平均变换:
X2={x2(1),x2(2),…,x2(n)},
(6)
式中,
(7)
2.2 灰色预测模型
将原始数据进行数据处理,得到指数单增序列,灰色预测模型能够较好地处理连续单增的数据,因此,对X2序列进行累加得到
X3={x3(1),x3(2),…,x3(n)} ,
(8)
式中,
(9)
将累加后的X3序列代入灰色模型白化微分方程:
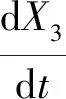
(10)
式中:a为发展灰数,反映对应序列的发展趋势;b为灰作用量,反映数据序列的变化关系。
进一步求得灰色模型灰色微分方程[16-19]:
x0(k)+az1(k)=b,
(11)
式中,
(12)
灰色微分方程对应的时间响应序列为
(13)
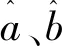
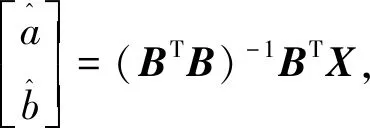
(14)
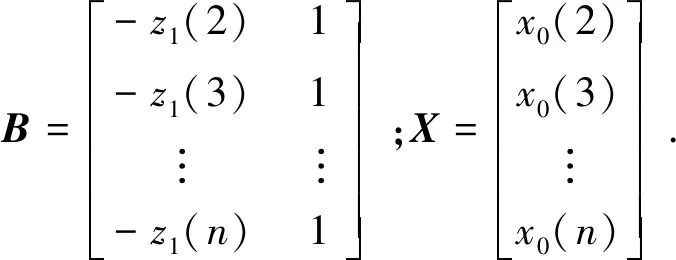
其中,
(15)
(16)
k=2,3,…,n,
(17)
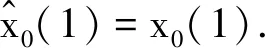
2.3 模糊C均值聚类法
模糊C均值聚类法,简称FCM算法,是以类内加权平方误差和最小为目标,将1组数据进行聚类,根据隶属度最大原则,将数据分为n个聚类中心点,并输出1个模糊划分矩阵,聚类中心点表示每个类的平均特征,可以认为这一类数据的代表点。利用原始数据与初步预测值之差进行聚类:
(18)
获得聚类中心点ci和模糊状态划分矩阵。
FCM算法相比于K均值方法的硬聚类,引入了隶属度概念,使得聚类结果更加灵活。FCM算法通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的[20-21]。
FCM算法给每个样本赋予属于每个簇的隶属度函数,通过隶属度值大小来将样本归类,一般步骤为:
1)确定分类数,指数m的值,确定迭代次数(这是结束的条件,当然结束的条件可以有多种)。
2)初始化一个隶属度U(注意条件,总和为1)。
3)根据U计算聚类中心ci.
4)计算目标函数J.
5)根据ci返回去计算U,回到步骤3,一直循环直到结束。
假定数据集为X,如果把这些数据划分成类,那么对应的就有c个类中心,每个样j属于某一类i的隶属度为uij,定义FCM目标函数为
(19)
约束条件为
(20)
式中:n为样本数;m为一个隶属度的因子;xj为第j个样本,是具有d维特征的一个样本;ci为i簇的中心,也具有d维度;‖xj-ci‖2表示欧式距离。
FCM不断迭代计算隶属度和簇中心,直至达到最优。
2.4 加权马尔可夫过程
马尔可夫一步转移概率矩阵为[22]
(21)
(22)
式中:Mij为状态i→j一步转移个数;Mi为状态i的个数;N为划分的状态空间的个数。
多步转移概率矩阵为
P(q)={P(1)}q,
(23)
式中,q为步长。
战时装备损耗量数据之间存在一定的联系,为了挖掘各个数据之间的联系,引入状态权重,根据划分的状态空间的个数N,依次求出所需预测时间点数据的前N个状态权重,依据数据之间的相互依存关系,进行加权状态和,最终确定所需预测时间点数据的状态,求得最终预测值。
原始数据序列的自相关系数为
(24)

将求得的自相关系数,进行数据归一化,得到状态权重θi:
(25)
为了确定所需时间点预测值数据的状态,将前面若干时间点数据作为初始值,根据前面历史数据到所预测值的时间点的步长,求得多步转移矩阵;最后计算权重和,确定预测时间点的所属状态空间:
(26)
式中:E为状态空间;Pj为历史时间点数据对应的状态空间。
根据最大隶属度原则max(Pi)所对应的即为预测时间点数据状态。则最终预测值为
(27)
式中,ci为第i状态对应的聚类中心点。
3 实例验证
目前关于战时装备损耗的相关数据记录少、获取困难,同时现有的数据具有保密性,无法公开。因此,为了验证提出的损耗预测方法应用于符合时间序列特性的数据的合理性和正确性,以及方法的优越性,笔者采用文献[23]中某航空弹药维修器材的损耗数据进行实验验证。将原始数据,经过加速指数变换和几何平均变换数据处理后,转换为连续增长型数据,并带入灰色预测模型,由式(1)~(17)得到初步预测值,如表1所示。

表1 航空弹药维修器材2006—2015年初步预测值
利用式(18)求得原始数据与初步预测值之差,并运用FCM,以类内加权平方误差和最小为目标,进行状态划分,获得聚类中心点和模糊划分矩阵。
图2表示不同的误差分类数下,类内加权误差平方和和迭代次数的关系。由图2可知,将误差值ΔE划分为4类,此时迭代次数最少,并且类内加权平方误差和最小。因此将误差值分为4类,得到的4个聚类中心点和模糊划分矩阵,如表2所示。
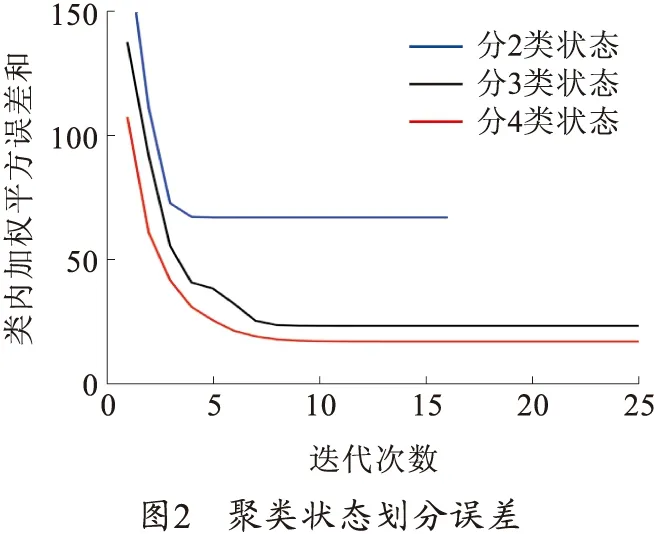

表2 聚类中心点和模糊划分矩阵
利用式(27),利用初步预测值和聚类中心点,可求得2006—2014年的改进型灰色-马尔可夫预测值,如图3所示。
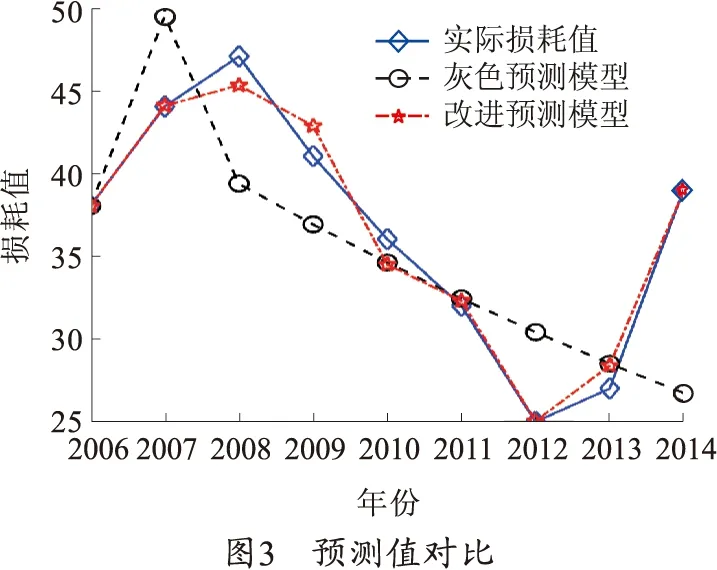
从图3可知,经过灰色预测模型得到的初步预测值,预测准确度较差,并且预测趋势与原始数据差距较大;而笔者提出的方法预测精度较高,并且能够较好地反映出数据的趋势走向。
分别计算出2006—2014年初步预测值与原始数据之差,由表2可求出对应每一年所处状态,由式(21)~(22)得到一步转移矩阵为

(28)
根据2006—2014年的数值预测2015年损耗量,为深度挖掘2015年数据与历史数据之间的关系,选择2011—2014年数据,由式(23)~(25)求得各阶转移概率矩阵和马尔可夫状态权重,具体如表3所示。
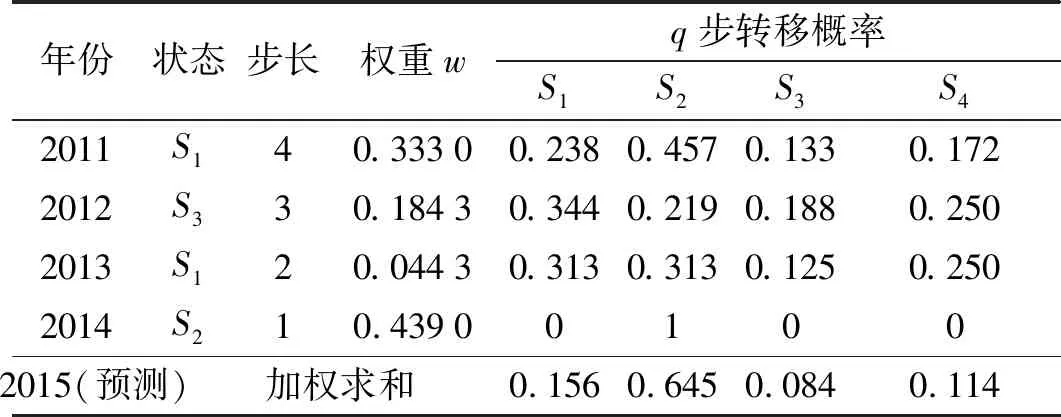
表3 2015年预测值表
由表3可知,由式(25),求出2015年数据对应状态的所占权重,根据最大隶属度原则,2015年损耗状态为状态S2,因此,根据式(27),得到2015年预测值,如图4所示。
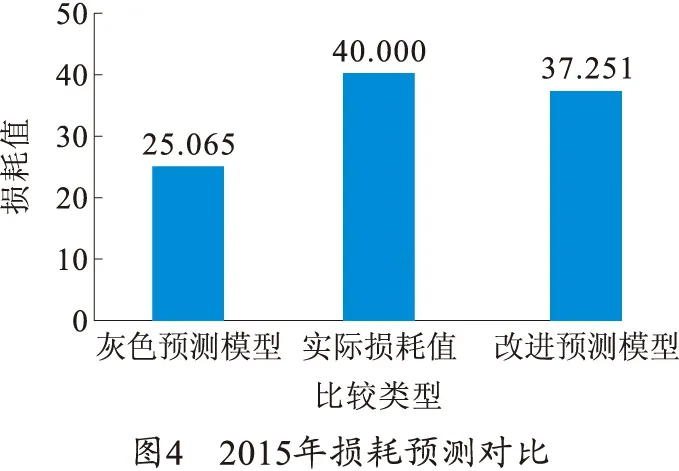
图4表明,灰色预测模型利用历史数据预测2015年损耗量,存在较大误差,而利用笔者所提方法,预测2015年损耗量,准确度较高,误差较小。
为了验证所提模型的预测精度,将原始数据分别带入灰色预测模型和改进灰色-马尔可夫预测模型,得到预测值,分别计算灰色预测模型和改进灰色-马尔可夫预测模型与原始数据之间的误差,得出绝对误差和相对误差量,如图5所示。
由图5可知,运用改进型灰色-马尔可夫模型,进行损耗预测分析研究,绝对误差和相对误差降低明显,误差较小,并且由图3得到,整个预测过程趋势和真实值损耗趋势更为接近,较好地反映了将来时刻损耗预测值的走向。
传统的装备损耗预测方法主要包括唯象型、唯理型方法和神经网络算法等。唯象型方法快速便捷,但精度不高,逐渐不适用于信息化、智能化战争时代的预测要求。唯理型方法,如兰彻斯特方程,通过解析法预测装备损耗。但现代战争中包含的诸多因素,复杂且多变,远远超出了兰彻斯特方程赖以建立的预先假设条件。而当下运用广泛的神经网络算法,需要大量的数据支撑,也不适用于战时装备损耗预测。笔者提出的基于改进型灰色-马尔可夫预测模型的损耗预测方法,简单快捷,预测精度高,同时对复杂不确定的因素进行模糊处理,能够得到较好的预测结果。

4 结束语
根据战时装备损耗数据呈振荡的特点,运用加速指数变换和几何平均变换方法,对原始数据进行处理,使其更好地适应于灰色预测模型,得到初步预测值。接着利用原始数据与初步预测值之差,运用FCM法,以类内加权平方误差和最小为目标,根据迭代次数最少和误差平方和最小,将数据分为4类,获得4个聚类中心点和模糊划分矩阵,进而求得一步转移矩阵,为了挖掘各个数据之间的关系,引入了马尔可夫状态权重,更加精确地确定预测时间点的所属状态,进而求得预测值。实验数据验证笔者所提方法预测精度较高,并且能够较好地反映出接下来时刻的损耗趋势。考虑战争中不确定因素的影响,结合战时记录数据,进一步优化模型,是接下来研究的重点。
