基于两阶段方法的垃圾中转站选址研究

2021-06-25李梦琦耿秀丽

软件导刊 2021年6期

李梦琦，耿秀丽

（上海理工大学管理学院，上海 200093）

0 引言

垃圾分类有利于垃圾回收、转运和再利用。生活垃圾的处理方式是将生活垃圾从垃圾收集点运输到垃圾中转站，在垃圾中转站处理不同垃圾。生活垃圾经过垃圾中转站分类处理之后，分别运送到各自的处理厂进行资源回收再利用。但是随着城市的发展，各地垃圾中转站数量缺少，亟需新建。科学合理确定垃圾中转站选址，不仅可以降低垃圾中转站与垃圾处理厂成本，还可减少对环境的影响。

垃圾回收、处理、运输等问题受到学者关注，对垃圾中转站选址展开了相应研究。胡文等［1］利用AHP 方法综合社会、自然环境、经济和交通因素建立垃圾中转站选址评价指标体系，运用GIS 的空间分析能力对垃圾中转站选址进行了研究；朱超平等［2］利用GIS 技术原理和AHP 方法对垃圾中转站进行评估分析并提出优化方案；肖迟仓等［3］通过ArcGis10.2 重分类对徐州市铜山县部分地区的农村生活垃圾中转站进行优化。以上文献在对垃圾中转站选址问题进行研究时，只对垃圾中转站选址影响因素进行了分析研究，没有对垃圾中转站建设费用以及在垃圾收运过程中的运输费用进行研究；张佳伟等［4］利用各垃圾箱分布点位置，以垃圾运输费最小为目标函数，利用偏导法建模，重心法求解，得到最优的中转站位置；王利娟等［5］建立以垃圾中转站建设成本、垃圾运输成本和垃圾分类管理成本之和最小为目标函数的混合整数数学规划模型，利用软件CPLEX对模型进行求解来研究垃圾中转站的选址问题；杨帆等［6］通过建立经济成本最小化和生态质量最大化的双目标规划模型对垃圾中转站选址进行研究；李海君等［7］考虑建设运营成本、负效应、回收效率的多目标整数规划模型，最终确定中转站位置、收纳量与服务分配方案；杜亚娟等［8］利用Floyd 算法获取整个网络中任意两节点的最短路长值，选取最小的选址半径，用中心转移算法解决垃圾中转站的最优选址问题；席芳娟等［9］利用混合整数规划模型，选取总运输成本最低的候选节点进行垃圾中转站选址；李倩茜等［10］以成本最小、环境负效应最小为目标函数建立多目标规划模型，用遗传算法进行求解，得出垃圾中转站选址方案。以上文献在进行垃圾中转站选址研究时，只考虑了费用最小化，没有考虑到垃圾中转站选址因素的影响。

综上所述，一些学者采用定性的分析方法比如AHP，一些学者采用定量方法如遗传算法、整数规划、混合整数规划和GIS 等，但定性分析方法只考虑了垃圾中转站选址的影响因素，没有考虑垃圾转运过程中的量化因素，如运输成本；定量分析方法只考虑了垃圾中转站的量化因素，如建设成本、垃圾转运过程中的运输成本等，缺乏对垃圾中转站选址的影响因素全面考虑。目前，很少有将定性和定量方法相结合进行垃圾中转站的选址研究。垃圾中转站选址不仅受到很多定性因素限制，而且在定量约束如垃圾转运过程中的运输成本等也需考虑。

本文采用定性和定量相结合的两阶段方法对垃圾中转站选址进行研究。第一阶段采用定性分析，考虑到垃圾中转站选址的评价指标较多且存在复杂的关联关系，采用PROMETHEEⅡ方法确定指标权重。专家根据确定好的指标权重对候选节点进行评价，利用三角模糊数将语义评价信息转换为具体数值。然后用PROMETHEEⅡ方法对候选节点进行排序，进行初步选址。第二阶段考虑垃圾转运过程中的运输成本和中转站数量，建立0-1 整数规划模型得到最优选址。选取河南省郑州市中原区垃圾中转站选址问题作为案例，选出可行的垃圾中转站。最后利用BWM确定权重方法和本文所提方法进行对比，验证本文方法的有效性。

1 基于PROMETHEEⅡ方法确定指标权重

垃圾中转站选址与周边的环境息息相关，受自然因素、市政公共设施和相关政策法律法规影响。由于中转站对环境、地表水、地下水以及土壤等都会产生污染，因此其建设需要远离水源，远离商业用地和绿地，远离医疗机构和学校。垃圾中转站选址一般要将土地利用类型、垃圾量密度和区域避让等作为评价指标。土地利用类型分为商业用地、绿地、住宅用地和工业用地。区域避让主要包括医疗机构、学校、政府机关、公园绿地、水系。土地利用类型和区域避让这两个评价指标有着紧密的关联关系，垃圾量和土地利用类型有着密切的关联关系，住宅用地的垃圾量密度大。此外，不同地区的垃圾中转站选址根据实际情况还会有其他评价指标，评价指标具有量多且复杂的特点。

第一阶段采用多属性决策方法对垃圾中转站进行定性分析得到初步选址，具体步骤如下：①根据垃圾中转站选址影响因素科学合理地确定评价指标；②建立评价指标之间的复杂网络图，计算各个评价指标的度中心性、介数中心性和网络凝聚程度这3 种网络属性；③根据评价指标的网络属性，利用PROMETHEEⅡ方法计算每一评价指标的净流量值，再计算每一评价指标净流量相对于最小净流量的差值，得到指标相对净流量。对该数据进行归一化处理即得到评价指标的权重；④将专家的评价语义利用三角模糊数进行处理，再利用PROMETHEEⅡ方法对候选节点进行净流量计算，将计算结果进行排序，确定初步选址。

1.1 评价指标的网络属性

在垃圾中转站选址问题研究中评价指标具有多样性，本文选取多个评价指标，考虑评价指标之间的关联关系，建立评价指标之间的复杂网络图。本文根据无向网络来表示两个指标之间的关联关系。如果两个评价指标之间有关联，就用无向直线进行连接，否则就不连接。

本文用度中心性、介数中心性、接近中心性来衡量评价指标的重要性。度中心性强调节点与相邻节点的连边数，一定程度上体现节点在网络中的直接影响能力。介数中心性的评价指标在整个评价指标中占有最重要的位置。接近中心性考虑节点与其他节点的接近程度，对于信息的传递与获取具有重要作用。

1.1.1 度中心性

度中心性在复杂网络节点重要性中是最直观的指标，表示节点在网络中与周围临近节点建立直接联系的能力。度中心性值越大，说明此评价指标权重越大。用ki表示与节点vi直接相连的节点数量，定义ki为节点vi的度，若在有N个节点的网络中，ki≤N-1，则归一化的节点度属性值CD（vi）［11］为：

1.1.2 介数中心性

介数中心性指标vi反映了节点的必经之地。介数中心性越高，该评价指标重要性越高。介数中心性数学表达式［12］如下：

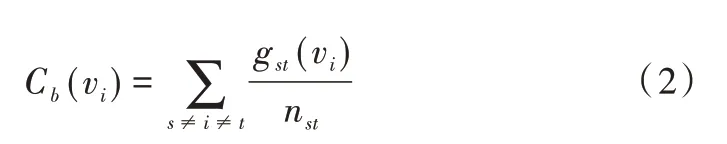
式中：gs（tvi）为节点vs和vt之间最短路径经过节点v的条数；nst为节点vs和vt之间的最短路径条数［12］，介数中心性值越大，表示评价指标越重要。

1.1.3 网络凝聚程度

网络凝聚程度指节点vi到网络其他所有节点距离之和的倒数。设dij为网络中节点vi到节点vj的最短距离，若在有N个节点的网络中，任一节点到达其他所有节点的最短距离之和，则归一化接近中心性属性值Cc(vi)［13］为：

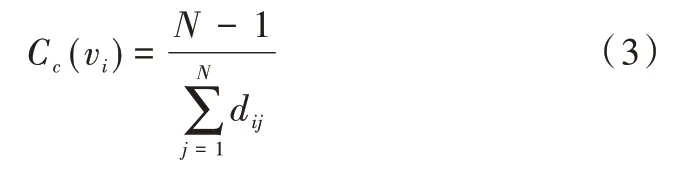
从复杂网络全局性来看，网络凝聚程度描述了节点与复杂网络中其他节点之间的联系，网络凝聚程度越高，表明该评价指标重要性越高。

1.2 确定指标权重

通过确定好的评价指标和评价指标网络属性，采用PROMETHEEⅡ方法确定指标权重步骤如下：

1.2.1 选择偏好函数

PROMETHEEⅡ方法中偏好函数的确定通常有6 种常用准则［14］，高斯型偏好函数与其他函数相比具有非线性变化特征，更符合实际的决策环境，因此本文选用高斯准则形式的偏好函数。

设有m个评价指标C=｛C1，C2…Cm｝，评级指标的网络属性值为kn（k1，k2，k3），分别表示评价指标的度中心性、介数中心性和网络凝聚程度的值。对网络属性值kn进行评价，得到指标Ci关于kn的属性值Cin。记Cin-Cjn=d，用高斯准则形式的偏好函数进行计算，其表达式如下：

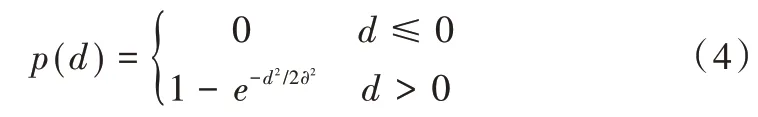
参数∂选取0.2，则P（d）为指标Ci相对于指标Cj在网络属性值kn上的偏好函数，有0 ≤p(d) ≤1。

1.2.2 计算指标的多属性偏好优序指数

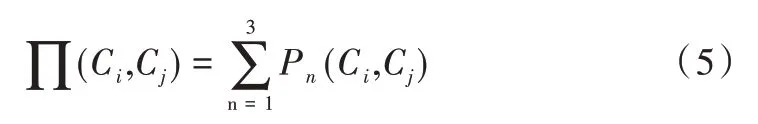
指标的多属性偏好优序指数∏(Ci,Cj)表示在考虑所有属性的条件下，指标Ci优先于Cj的程度［7］。

1.2.3 计算指标流出量

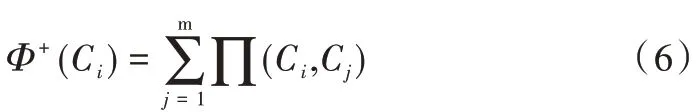
指标Ci的流出量Φ+(Ci)表示指标Ci优于其他指标的程度。

1.2.4 计算指标流入量

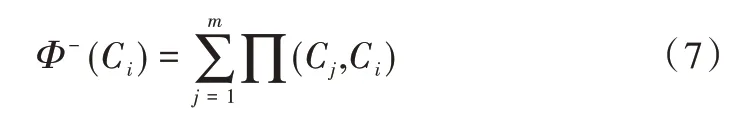
指标Ci的流入量Φ-(Ci)表示其他所有指标优于指标Ci的程度。

1.2.5 计算指标净流量

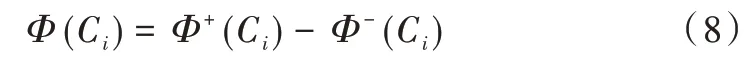
式中指标净流量Φ(Ci)是指标Ci的优先程度反映，Φ(Ci)值越大说明指标Ci的优先级别越高。

1.2.6 计算指标权重

根据指标净流量值得到评价指标的重要度排序，计算每一指标净流量相对于最小净流量的差值pi：

将各指标的相对净流量pi进行归一化处理，即可得到各指标的权重wi：

2 确定初步选址

根据确定好的指标权重，计算每个评价指标下候选节点两两比较的优劣程度，并据此计算出每个候选节点流出量、流入量和净流量，采用模糊PROMETHEEⅡ计算得出每个专家评价下候选节点的优先关系排序结果。基于模糊PROMETHEEⅡ方法对垃圾中转站候选点排序确定初步选址。

（1）使用三角模糊数处理评价信息。由专家对评价指标进行打分，然后采用三角模糊数来处理评价信息。任意三角模糊数M=（l，m，u）满足m≤l≤n，且m，l，n在0～1 之间。

定义1［15］每个三角模糊数都对应一个非模糊数，设M=（l，m，u）为一个三角模糊数，其对应的非模糊数S（M）为：

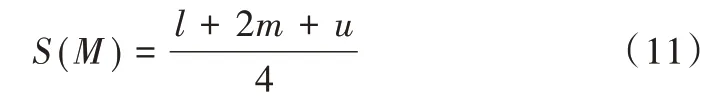
（2）确定评价指标权重。垃圾中转站评价指标有m个C=｛C1，C2…Cm｝，将专家利用三角模糊数得到的评价信息所获得的权重和根据式（9）和式（10）得到的指标相乘，得到权重W=｛w1，w2…wm｝。

（3）确定偏好函数。假设垃圾中转站的候选节点有q个A=｛A1，A2…Aq｝，评价指标有m个C=｛C1，C2…Cm｝。按照评价指标Ct进行评价，得到候选节点Ai关于Ct的属性值Ait。记Ait-Ajt=d'，参照式（4），则p(d')为方案Ai相对于方案Aj评价指标Ct上的偏好函数，有0 ≤p(d') ≤1。

（4）计算候选节点的多属性偏好优序指数。

（5）计算方案Ai的流出量Φ+(Ai)和流入量Φ-(Ai)。

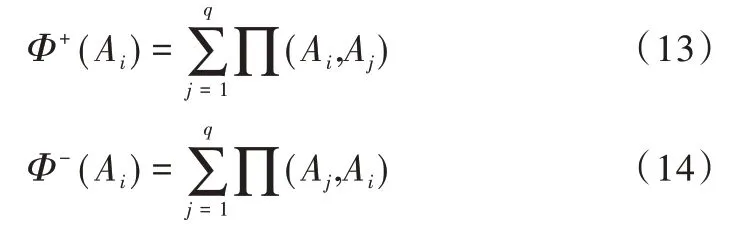
式中：Φ+(Ai)表示节点Ai优于其他节点的程度，Φ-(Ai)表示节点Ai劣于其他节点的程度。

（6）计算候选节点偏好净流量Φ(Ai)。

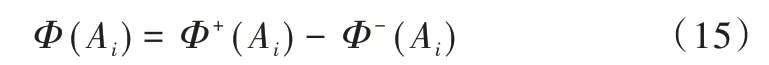
根据净流量大小Φ(Ai)对垃圾中转站的候选节点进行排序，是PROMETHEEⅡ方法衡量方案优劣的主要依据。根据净流量的大小对候选地址进行初步排序，确定初步选址。

3 选址优化

通过PROMETHEEⅡ方法对垃圾中转站进行初步选址后，选出排名靠前的候选地址。根据初步选址结果，再考虑垃圾转运过程中运输成本最小化目标建立目标规划模型，然后选出最优节点。

（1）符号参数设定。在目标规划中设定参数、集合的符号如表1 所示。

Table 1 Symbol Description表1 符号说明

（2）0-1 规划模型构建。本文以垃圾收集点到垃圾中转站及垃圾中转站到垃圾处理厂的运输费用最小和为目标函数，建立0-1 规划模型。

目标函数（16）表示垃圾在整个转运过程中的运输费用，其中，第一项是从垃圾收集点i到垃圾中转站j一年的运输成本，第二项是从垃圾中转站j到垃圾处理厂k一年的运输成本。约束条件（17）表示垃圾中转站需要选取的数量为P 个，约束条件（18）表示垃圾收集点i被垃圾中转站覆盖的集合中至少选择一个，约束条件（19）表示每个居民点的垃圾只能运往一个中转站，约束条件（20）表示每个中转站的垃圾只能运往一个处理站，约束条件（21）表示只有先在节点j处建中转站，居民点i的垃圾才可以运往节点j，约束条件（22）表示变量只能选择0 或1。

4 实例分析

郑州市作为全国首批46 个垃圾分类试点城市之一，生活垃圾分类管理办法已于2019 年12 月12 日开始正式实施，在垃圾收集、转运、处理过程中，垃圾中转站起着非常重要的作用。目前郑州市垃圾中转站数量较少且分布不均匀，对于实施垃圾分类是一个大问题。本文以郑州市中原区为例，对中原区的垃圾中转站进行选址研究，需要对中原区选取4 个垃圾中转站。在中原区选取15 个候选地址，如图1 所示，图中英文字母为垃圾收集点标注，阿拉伯数字为垃圾中转站的候选节点。

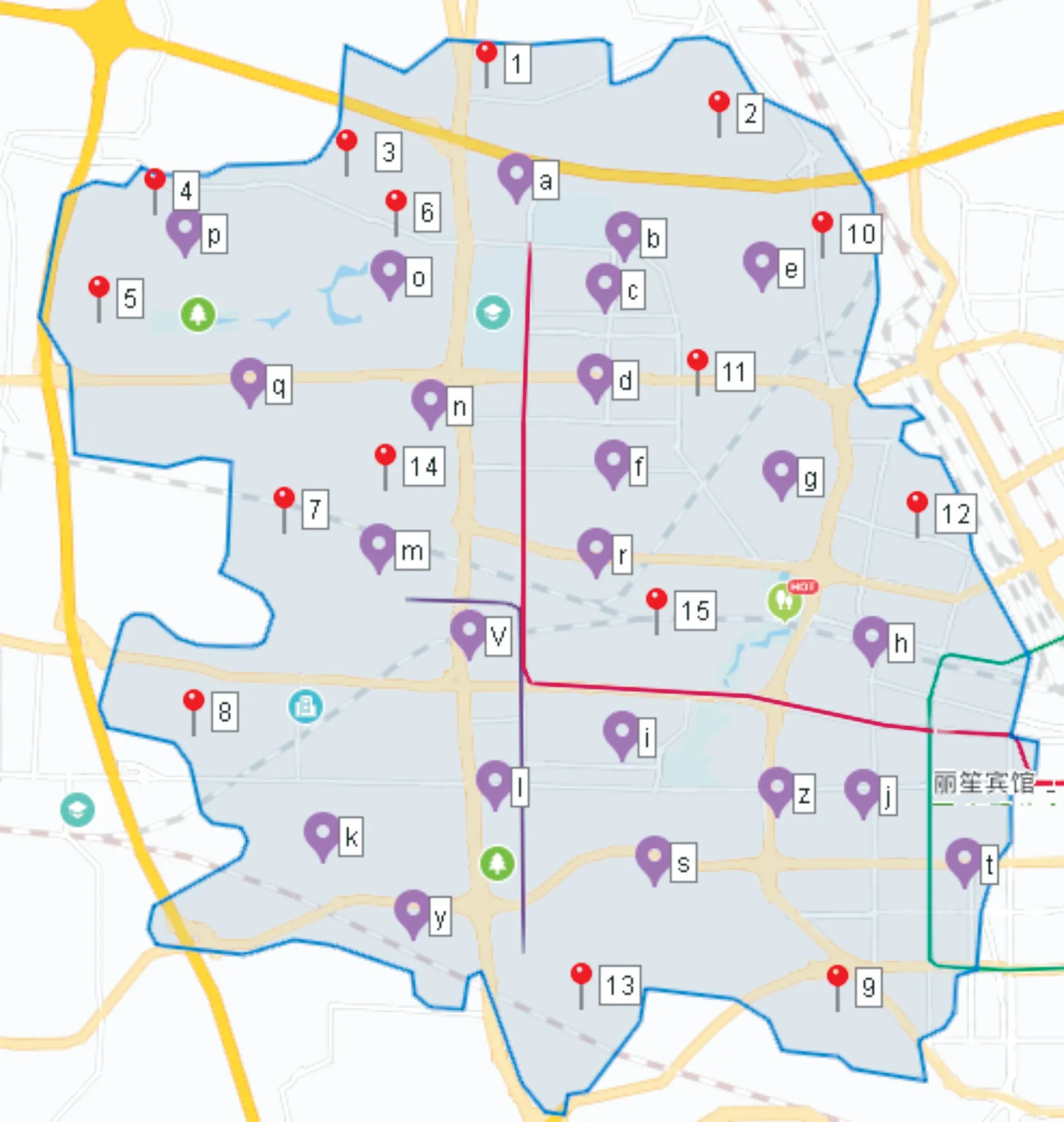
Fig.1 Candidate location of garbage transfer station图1 垃圾中转站候选位置

4.1 确定指标权重

本文从自然因素、区域因素、区域避让3 个方面确定评价指标，自然因素包括土地使用类型C1、环境污染C2；区域因素包括收集半径C3、垃圾产量C4以及垃圾的收集密度C5；区域避让包括政府机关C6、医疗机构C7、学校C8、公共绿地C9、水系C10；具体指标符号如表2 所示。

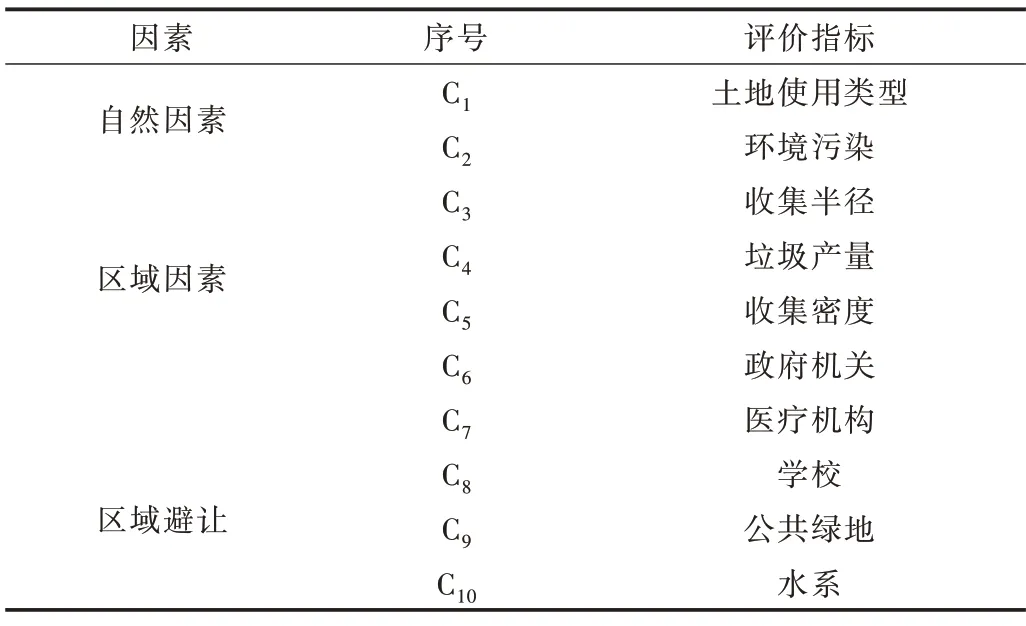
Table 2 Site selection evaluation index of waste transfer station表2 垃圾中转站选址评价指标

本文垃圾中转站选址评价指标权重根据指标之间的关联关系确定，专家根据指标对候选节点进行评价，然后进行语义转换共同确定。首先根据专家对指标之间的关联关系进行确认，如果两个指标之间存在关联关系，两个指标之间就存在一条无向边，否则就不存在无向边。根据专家的评级结果绘制指标之间的关系如图2 所示。

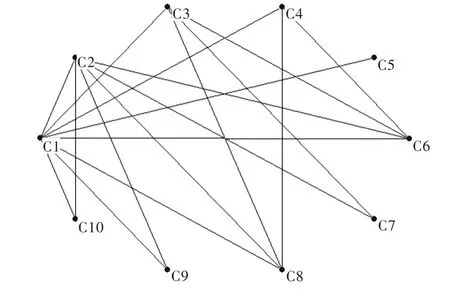
Fig.2 Evaluation index relationship of waste transfer station图2 垃圾中转站评价指标关系

利用pajek 软件和公式（1）-（3）计算出评价指标的网络属性如表3 所示。

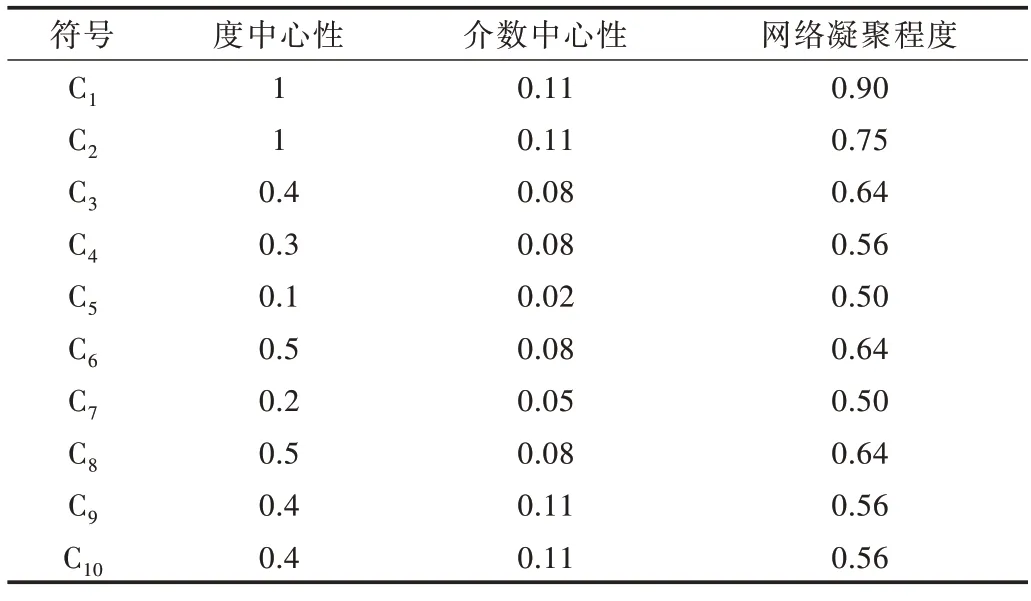
Table 3 Network attribute value of evaluation index表3 评价指标的网络属性值

根据公式（4）-（8）计算指标的净流量值，如表4 所示。

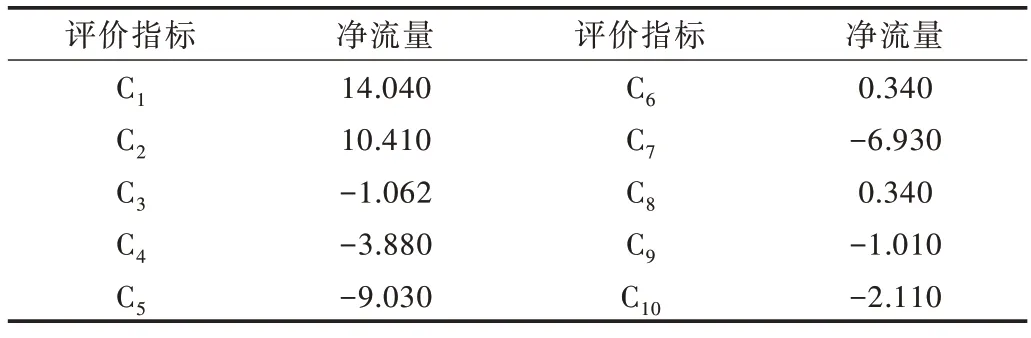
Table 4 Net flow value of evaluation index表4 评价指标净流量值

根据公式（9）计算指标权重并对指标进行归一化处理，如表5 所示。

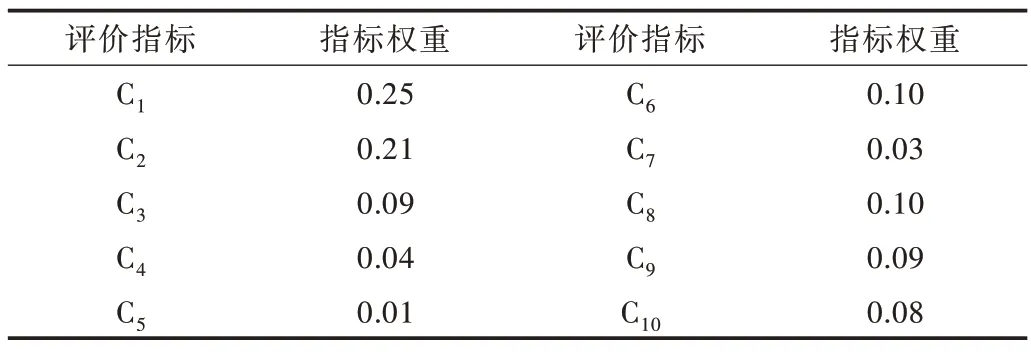
Table 5 Weight of evaluation index表5 评价指标权重

4.2 初步选址

垃圾中转站的选址涉及到环境、土地以及收集半径等，所以选择5 位地质研究者、10 位资深物流专家以及5 位环境研究者组成专家组，对评价指标进行打分。本次垃圾中转站候选点有15 个，20 位专家分别对每个候选点进行现场考察并打分。利用三角模糊数进行语义评价，然后利用表6 中的语义评价变量与三角模糊数之间的转换关系进行转换。

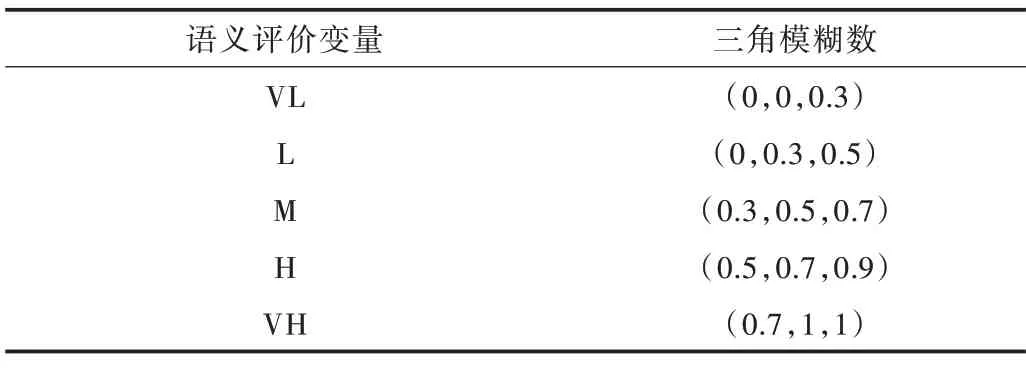
Table 6 Transformation relationship between semantic evaluation variables and triangular fuzzy numbers表6 语义评价变量与三角模糊数之间的转换关系

专家组对各个指标进行评价，根据每个指标的语义优劣进行评价并将语义转换为三角模糊数，采用算术平均法对每个专家的语义评价根据公式（10）进行计算，然后对候选节点进行评价。其中对候选节点1的评价结果如表7所示。

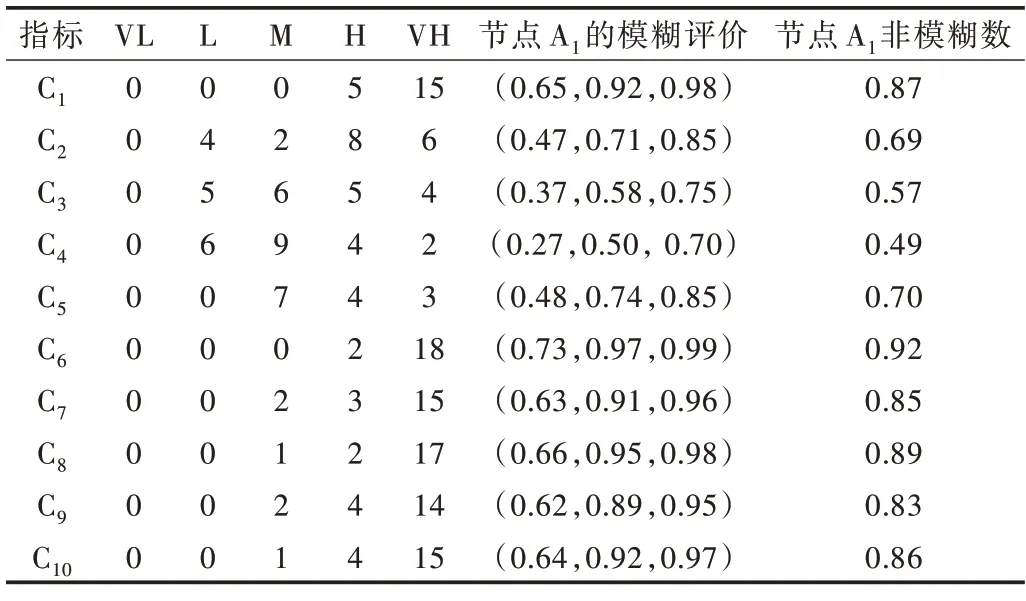
Table 7 Evaluation results of candidate node 1 by experts表7 专家对候选节点1 的评价结果

其他候选节点专家评价结果如表8 所示（其他节点计算步骤省略）。

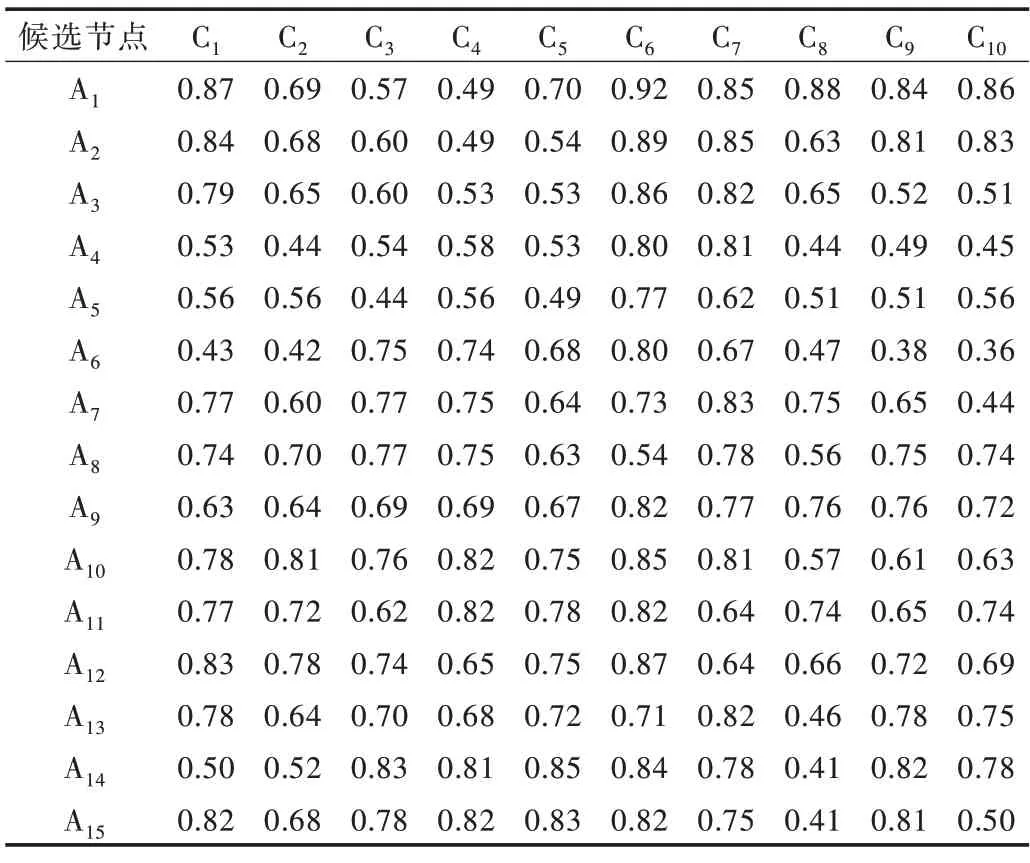
Table 8 Evaluation results of candidate nodes by experts表8 专家对候选节点的评价结果

根据公式（12）-（15）计算出候选地址净流量，结果如表9 所示。

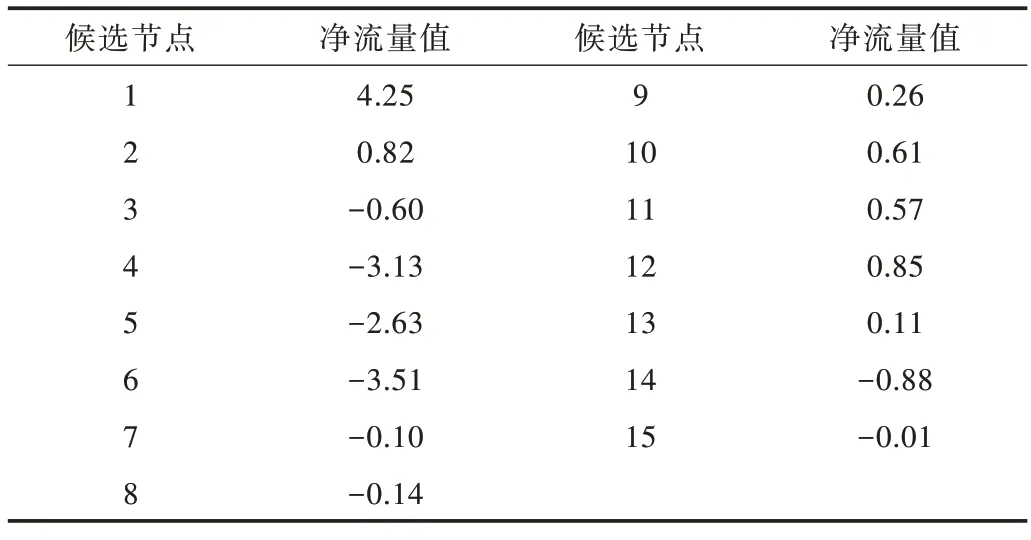
Table 9 Calculation results of net traffic of candidate addresses表9 候选地址净流量计算结果

通过对候选地址进行净流量值计算，对15 个候选地址进行排序，根据表9 排序结果得到初步选址，将节点A3、A4、A5、A6、A14排除，对剩下的节点进行优化选址。

4.3 利用0-1 规划优化选址

4.3.1 选址结果分析

候选节点初步选址之后，对剩下的候选节点进行优化，通过计算垃圾收集点到垃圾中转站的运输费用和垃圾中转站到垃圾处理站的运输费用，对中原区垃圾中转站进行选址，选出4 个垃圾中转站，能够将所有的垃圾收集点进行覆盖。建立0-1整数规划模型，用Lingo软件对模型求解。

将垃圾收集点到垃圾中转站的每单位运输费用（β）设定为6 000 元，从垃圾中转站到垃圾处理场的每单位运输费用（w）设定为8 000 元。垃圾收集点到垃圾中转站的距离，以及垃圾中转站到垃圾处理厂的距离都由百度地图测距得出。求解结果X8、X9、X10、X12的值为1，其他X 的取值为0，目标函数的最小值为752 万元。

此时垃圾中转站的最优选址是A8、A9、A10、A12，垃圾中转站对垃圾收集点之间的覆盖如表10 所示。

Table 10 Coverage between garbage transfer station and garbage collection point表10 垃圾中转站与垃圾收集点之间覆盖情况

垃圾中转站A8 负责收集点m、n、o、p、q 的垃圾收运，垃圾中转站A9负责垃圾收集点l、i、j、k、s、t、y、z 的垃圾收运，垃圾中转站A10负责垃圾收集点a、b、c、e 的垃圾收运，垃圾中转站A12负责垃圾收集点d、f、g、h、r 的垃圾收运。

4.3.2 结果对比分析

为对比本文所提确定指标权重方法的有效性，用BWM方法确定指标权重并进行对比分析。通过对评价指标进行计算，确定指标的权重如表11 所示，用公式（12）-（15）通过PROMETHEEⅡ方法对垃圾中转站候选节点进行排序，其净流量计算如表12 所示。

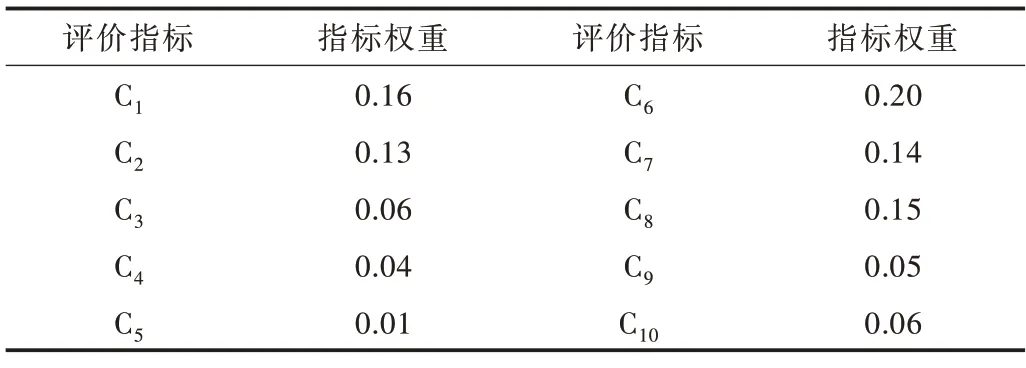
Table 11 BWM method to determine index weight表11 BWM 方法确定指标权重

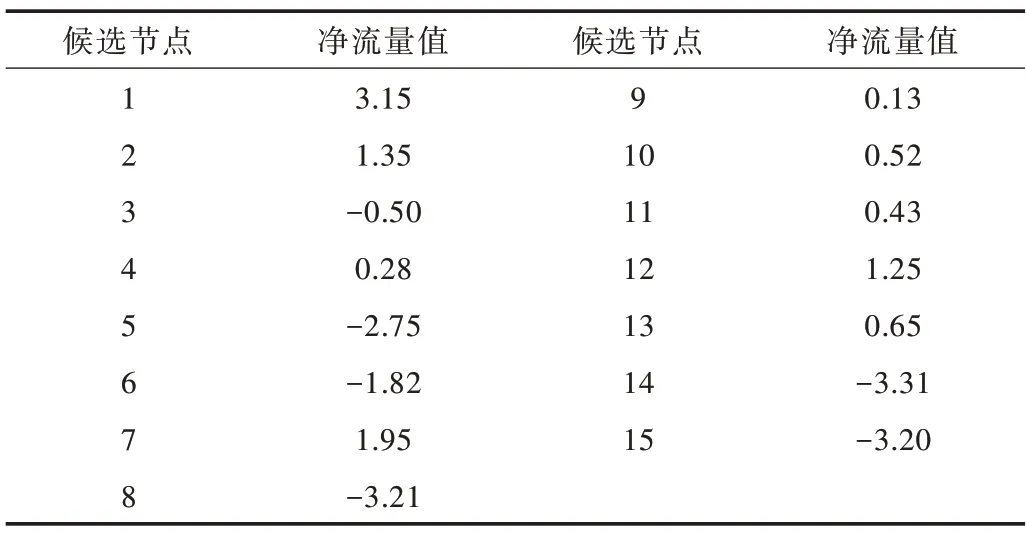
Table 12 Calculation results of net flow value of comparison results表12 对比结果净流量值计算结果

对比表5 和表11 用不同的方法确定评价指标权重，发现用BWM 方法确定的指标权重中评价指标C8（学校）和评价指标C9（公共绿地所）占的权重较大。PROMETHEEⅡ方法确定指标权重中，指标C1（土地使用类型）和指标C2（环境污染）占的权重比较大。按现实情况考虑，在进行垃圾中转站选址时，土地使用类型和对于环境污染的程度应该优先考虑。根据表12 中净流量值进行排序，对比之前的排序结果，只有节点1 和节点2 的排序结果是一样的。根据排序结果将节点A5、A6、A8、A14、A15排除，剩下的10 个节点为初步选址结果。

再利用本文提到的0-1 整数规划模型对选址进行优化，其输出结果为1 的节点是：节点A7、A11、A12、A13，目标函数值为793.4 万元。垃圾中转站与垃圾收集点之间的覆盖关系如表13 所示。

Table 13 Coverage of garbage transfer station and garbage collection point in comparison results表13 对比结果中垃圾中转站与垃圾收集点覆盖情况

垃圾中转站A7负责收集点m、n、o、p、q、v 的垃圾收运，垃圾中转站A11负责垃圾收集点a、b、c、d、e 的垃圾收运，垃圾收集点A12负责垃圾收集点f、g、h、j、r、t 的垃圾收运，垃圾收集点A13负责垃圾收集点l、i、s、y、z 的垃圾收运。

本文中的评价指标土地使用类型、环境污染与政府机关、医疗机构、学校、公共绿地、水系都有关联关系，所以本文方法得出的指标C1土地使用类型和指标C2环境污染相比于其他指标权重比较大。用BWM 确定权重的方法和本文所提的复杂网络属性和PROMETHEEⅡ相结合的方法进行对比，发现BWM 没有考虑到评价指标之间的关联关系，致使所得到的权重不够合理。所以，由于评价指标的权重不同，垃圾中转站初步选址的结果就不同，在第二步优化选址过程中得到的结果也不同。本文提出的选址方法比对比方法选址费用少了41.4 万元，节省了5.5%，通过对比分析可以看出本文方法的有效性。