航天器火工冲击环境数据外推技术研究
2021-06-25任德鹏贺晓洋
李 青,任德鹏,杜 青,贺晓洋
(北京空间飞行器总体设计部,北京 100094)
0 引 言
航天器火工冲击环境来源于航天器与运载火箭分离解锁、器间舱段分离解锁、太阳翼和天线等机构解锁展开所产生的火工装置爆炸冲击。火工冲击环境是典型的高频瞬态环境,其主要频率范围为100~10000 Hz。在爆炸源附近,加速度时间历程呈现高幅值衰减型振荡,持续时间很短,一般在20 ms以内。它以应力波的形式在结构中传播,结构对它的响应只有微小的运动。结构中的运动响应近似于许多复杂的衰减正弦波叠加,响应加速度幅值随着距爆炸源距离的增加而迅速衰减,具有瞬态非平稳特性[1]。
航天器火工装置解锁过程中产生的爆炸冲击环境会导致航天器产生宽频带、高加速度、小位移、持续时间短、高频极为丰富的瞬态机械响应。在冲击过程中,爆炸的能量迅速传递到航天器及其组件上,所产生的位移、速度和加速度的突然变化有可能造成航天器结构和仪器、仪表等组件的损坏及故障,从而导致航天器无法正常工作。它会引起晶体、陶瓷、环氧树脂、玻璃外壳等脆性材料的裂碎;焊点及导线接点断裂;密封损害;多余物导电微粒的迁移(可产生间歇故障);继电器和开关的颤抖和转换;引起微小轻质结构(如微电子芯片)的变形等。因此,航天器及其各组件均需在地面进行爆炸冲击环境的模拟试验,尤其对于电工电子组件是必做的环境试验项目[2]。
在进行组件冲击试验之前,必须先获取或预示航天器火工冲击环境,并制定相应的组件冲击试验条件。由于火工冲击环境具有高频率、宽频带、瞬态、高加速度幅值和强非线性的特性,使得对其进行准确预示的难度很大。结构上的冲击环境由火工冲击源爆炸产生的冲击波和结构特性共同决定,通常根据当地冲击响应量级、频率成分以及到冲击源的距离将火工冲击环境分为近场、中场和远场[3-4]。目前工程实践中获取或预示航天器火工冲击环境的方法主要可分为三类:试验法、数值分析法和数据外推法。
试验法是获取航天器火工冲击环境最有效、最直接的方法。航天工程型号中,为了获取火工爆炸在结构上产生的真实冲击响应,进而制定组件冲击试验条件,往往采用真实的火工装置和真实结构进行火工装置爆炸冲击试验,常见的有器箭分离试验、太阳翼解锁展开试验等。考虑到火工装置产生的冲击响应具有一定的离散性,原则上真实火工冲击试验应重复进行3次及以上[5]。试验法的优势在于可以产生最真实的火工冲击环境,但是其试验成本高、只能获得有限的测点数据、具有后验性,在型号研制初期通常难以实施。
为了在型号研制初期实现火工冲击环境的预示,国内外学者对航天器火工冲击建模理论和数值分析方法进行了大量研究,包括统计能量分析(SEA)法、虚拟模态综合与仿真(VMSS)法、Hydrocodes法、FE-SEA混合法等。SEA法将一个复杂的系统划分为若干子系统,以各子系统输入、输出和耗散的“能量”为基本自变量建立子系统功率流平衡方程,进而求解得到每个子系统的能量响应平均值;Ullio等[6]通过对比有限元分析、统计能量分析结果与试验实测结果的一致性,指出了传统有限元分析方法在处理高频火工冲击问题时的缺点,建议采用统计能量分析法进行冲击响应的预示;然而,由于采用了统计平均的概念,该方法无法得到结构上具体位置的响应,仅能得到在一个区域上某个频段内的响应包络,因此主要用于中、远场高频冲击响应的预示。VMSS法首先估计出稳态频率响应幅值的包络,这个频率响应既可以是统计能量分析的稳态解、也可以是有限元分析的结果、还可以是直接测量的试验结果,在高频段假设该频率响应包络能够用分频段的局部振动模态来表达,其动力学方程与经典的模态综合方法形式相同;Lee等[7]采用SEA和VMSS结合的方法对某低轨地球观测卫星与运载火箭的分离冲击响应进行了预示,讨论了不同细化程度的模型在VMSS计算中的准确性,结论认为简单模型对冲击响应的预示更准确;王军评等[8]采用VMSS法对航天典型结构进行了建模,完成了运载火箭级间分离冲击响应预示;VMSS法既可以计算时域响应,也可以计算冲击响应谱(SRS),对于具有线性特性的结构可以估计近场响应。Hydrocodes法能够对爆炸和燃烧的详细过程进行时域建模,采用拉格朗日/欧拉网格描述非线性结构变形和分离,并模拟结构中应力波的产生和传播;Zukas[9]系统地介绍了Hydrocodes法的基本原理;赵欣等[10-11]采用Hydrocodes法建立了火工装置“振源系统—近场结构”一体化模型并分析了爆炸载荷在分离螺母内部的传递机制,得到了星箭界面分离载荷的形成机理;Hydrocodes法理论上可用于分析从冲击源、近场、中场到远场的各类冲击问题,但是对于复杂航天器上火工冲击响应的预示,受到动力学建模、计算量和计算时间等约束条件的限制。FE-SEA混合法根据模态密度将整个系统分为若干子系统,对于模态密度低的子系统采用有限元法建模,对于模态密度高的子系统采用统计能量法建模,被认为是一种处理冲击问题的有效手段[12];Troclet等[13]采用FE-SEA混合法对Ariane-5火箭的设备安装底座在中高频瞬态载荷作用下的响应进行了预示,将有限元分析结果作为统计能量分析的输入,得到了较为准确的分析结果;赵宏达等[14]联合FE-SEA混合建模技术和VMSS法对某型复杂卫星结构上的火工冲击响应进行了计算分析,计算结果的冲击响应谱曲线基本包络在试验结果的±6 dB范围内;FE-SEA混合法能够综合有限元法和统计能量法的优点,取长补短,但是有限元子系统和统计能量子系统之间的输入输出连接极为复杂,且子系统的划分准则不同对分析结果影响很大,所以该方法在工程应用中的可靠性仍未被证实。综上,各种数值分析法具有各自的优点和缺点,可用于研究航天器火工冲击环境产生和传递的机理,但是由于火工冲击响应对火工品装药量、火药参数、火工装置结构设计、材料工艺参数、安装及压紧形式、接触应力状态、结构预应力状态等因素的微小变化非常敏感,导致在实际型号应用中数值分析预示结果与试验结果相差甚远,相对误差能达到200%以上,即使在后期通过试验数据修正模型来减小误差,这种修正方法也通常是局部试凑性质的,不具有通用性和预示性。其根本原因在于所建立的分析模型无法完全模拟上述实际产品状态中所存在的敏感因素,对爆炸冲击源和传递结构的建模细节存在不准确性或不确定性。
鉴于数值分析法在实现航天器火工冲击环境准确预示上的难度,欧美等航天强国在航天器研制初期较多地采用数据外推法进行冲击环境预示[4,15]。数据外推法无需对火工装置和结构进行详细的建模,即可快速估算结构上的冲击响应环境,可为航天器构型布局方案的确定、组件冲击试验条件的制定等设计工作提供重要参考。另外,数据外推法还可以在一定程度上弥补试验法测点有限的缺点,可利用有限的测点数据来外推出任意无测点位置的冲击环境。本文详细总结了国内外航天器火工冲击环境数据外推技术的研究进展,分析了欧美不同数据外推公式(ESTEC rule和NASA rule)的差异和适用范围,在此基础上,结合我国航天器火工冲击环境数据和理论分析,提出了新的数据外推公式(称为CAST rule),通过与大量试验数据的对比分析,证明CAST rule具有更好的预示精度和更宽的适用范围。
1 研究进展
数据外推法主要根据火工冲击源的冲击响应谱以及冲击传递经过的距离、连接界面等快速估算航天器结构上某一区域或组件安装处的冲击响应谱,是一种工程实用的火工冲击环境预示方法,最早由美国NASA[4]提出,其主要步骤如下:
1)确定每个火工冲击源到各组件安装处的距离;
2)建立每个火工冲击源的冲击响应谱;
3)计算冲击响应从每个火工冲击源到每个组件的距离衰减;
4)计算冲击响应经过每个连接界面时的额外衰减;
5)对于一个结构区域内安装的所有组件,确定最大期望飞行环境;
6)在最大期望飞行环境基础上增加一定余量,以获得试验冲击响应谱。
NASA-HDBK-7005[4]给出了不同类型点源附近(10~13 cm)的冲击响应谱(在冲击响应谱的计算中,通常取阻尼比为0.05,对应的放大因子为10,本文中默认采用该取值)和冲击响应谱随距离的衰减规律,分别如图1和图2所示。当估算冲击响应经过连接界面的额外衰减时,NASA[4]建议每经过一个连接界面冲击响应谱峰值约衰减40%,最多计及三个连接界面,而对于冲击响应谱的上斜坡段不考虑衰减。这种方法存在的缺点是:需要不同火工冲击源的近场或中场冲击响应谱数据,而可靠的冲击源数据非常有限;由图2估算出的冲击响应谱在某些频率处的预示精度很差。早期的数据外推法由图1建立火工冲击源的冲击响应谱,由图2计算冲击响应谱随距离的衰减,又被称为经验模型法。

图1 不同类型火工冲击点源附近的冲击响应谱Fig.1 Shock response spectra for various point source pyrotechnic devices

图2 冲击响应谱随距离衰减规律Fig.2 Shock response spectrum versus distance from pyroshock source
随着大量火工冲击试验数据的积累,由一个参考航天器上的实测冲击响应数据外推得到一个具有相似设计的新型航天器上冲击响应的数据外推技术应运而生。数据外推技术的两个关键操作是火工冲击源的能量推算和距离推算。
令Er和En分别为参考航天器和新型航天器上火工装置释放的总爆炸能量(一般与火工品装药量成正比),那么新型航天器上的冲击响应谱Sn(f,d1)与参考航天器上的实测冲击响应谱Sr(f,d1)存在如下推算关系:
(1)
其中,d1表示响应点到火工冲击源的距离,f表示冲击响应谱的频率。一般来说,新型航天器与参考航天器所采用的火工装置和结构构型等设计的相似程度越高,式(1)的准确度越高。
得到火工冲击源处的响应后,可根据图2中的冲击响应谱随距离衰减规律推算任意关注点处的响应。由于图2不能很好地反映冲击响应谱衰减规律与频率的关系,NASA-HDBK-7005[4]给出了另一个描述冲击响应谱随距离衰减的推算公式:
(2)
式中:S(f,d1)和S(f,d2)分别为距离火工冲击源d1处(参考点)和d2处(预测点)的冲击响应谱,d=d2-d1。式(2)既可以与式(1)联合使用来推算新型航天器上关注点的冲击响应谱,也可以单独使用来推算原航天器上新增关注点的冲击响应谱,下文称为NASA rule。
需要注意的是,式(2)是由复杂桁架结构的点源火工冲击测量数据拟合而来,并不具有通用性。但是由于其具有简洁和易用的优点,NASA rule经常被应用于各种冲击源和结构构型的估算。
欧洲ESA-ESTEC结合大量的包带分离冲击测量数据,对NASA rule进行了适应性改造。基于SMART-1、Cluster、ROSETTA、Spot5和Eurostar 3000等型号的试验数据,ECSS-E-HB-32-25A[15]给出了适用于包带分离冲击的数据外推公式,称为ESTEC rule:
(0.0144d3-0.2d2+0.93d+0.024)}
(3)
ESA-ESTEC通过一个案例对比了ESTEC rule与NASA rule的预示精度。如图3[15]所示,相对于NASA rule,ESTEC rule在所有频率范围内的预示曲线更接近试验曲线。NASA rule的预示结果比实测结果偏低,特别是在高频段。
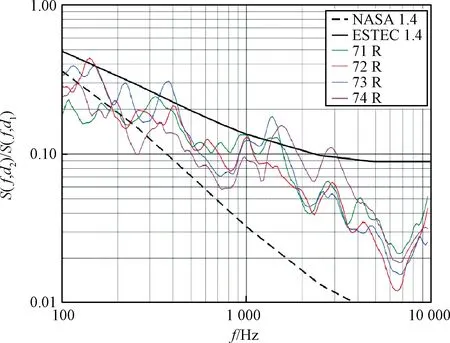
图3 ESTEC rule、NASA rule冲击响应预示曲线与试验曲线的对比示例(d=1.4 m)Fig.3 Example of validation of ESTEC rule by comparison with actual test and comparison against NASA rule (d=1.4 m)
最后,对于冲击响应通过连接界面时的衰减,国内外并没有统一的推算方法,这与连接界面的类型、界面对波的反射和折射特性等都有关。NASA[4]建议由连接界面导致的衰减量范围取为20%~75%。国内,丁继锋[16]基于对我国某卫星平台星箭分离冲击问题的研究,认为铆接等刚性连接一般不会造成冲击响应的衰减,而常见的螺接则会造成30%~60%的衰减;如果在连接界面上增加缓冲材料,过界面冲击响应的衰减量还会增加30%左右。
2 理论推导
通过上文的综述,可知式(2)和式(3)都是针对某一类火工冲击源和结构构型的试验数据拟合得来的,具有各自的使用局限性,特别是两个公式均与材料的弹性模量、密度等参数无关,这显然是不合理的。本节从火工装置爆炸产生的冲击波在弹性结构中的传播理论入手,研究冲击响应的衰减规律。
火工装置爆炸在结构中产生的冲击波初始主要为压缩波。由于工程上关心的结构响应不包含火工装置上的塑性变形区域,因此该冲击波在结构中的传播属于弹性力学的范畴,应符合弹性应力波的传播规律。在关于应力波传播的工程实践研究中,地震学对于地震波在地壳中的传播规律研究得最早,其研究成果对于本节的冲击波在结构中的传播规律研究具有一定借鉴意义。
在台站i观测到震源j引起的傅里叶振幅谱(观测谱)可以表示为[17]:
Aij(f)=Oj(f)Si(f)Gij(d)Bij(f,d)
(4)
式中:Oj(f)为频率为f时震源处的傅里叶振幅谱(震源谱),Si(f)是观测场地和仪器的响应,Gij(d)是路径距离为d处的几何扩散因子,Bij(f,d)是地震波传播时阻尼衰减因子。可见,其中与地震波传播规律相关的只有两项:Gij(d)和Bij(f,d),它们都是传播距离d的函数。
几何扩散因子Gij(d)与频率无关,通常可被写成
(5)
其中,系数k与波的类型有关:对于体波,取k=1;对于面波,取k=0.5。文献[18]给出了几何扩散因子与式(5)不同的分段表达式,可见该项需要根据实际情况凭借一定经验确定。
阻尼衰减因子Bij(f,d)主要由介质的品质因子Q决定,其表达式为:
(6)
其中,v为波速。在地震学中主要关心的是横波,横波波速约为纵波波速的一半。
2.1 阻尼衰减因子
下面采用经典多自由度系统振动理论对式(6)的阻尼衰减因子进行推导和分析。
有阻尼的n自由度系统的强迫振动方程可以表示成[19]:
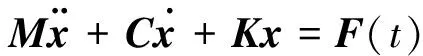
(7)
式中:M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,F(t)为载荷向量,x为位移向量。式(7)中C=0时的系统称为相应的无阻尼系统,假设通过模态分析已经得到它的振型矩阵Φ,相应的模态坐标向量为η,则存在如下坐标变换关系:
x=Φη
(8)
因此,式(7)可以写成
(9)
式中:P(t)=ΦTF(t)为模态载荷向量,模态质量矩阵Mp=ΦTMΦ=diag(Mp1)和模态刚度矩阵Kp=ΦTKΦ=diag(Kp1,Kp2,…,Kpn)为对角阵,而模态阻尼矩阵Cp=ΦTCΦ一般为非对角阵。
为了使式(9)能够解耦,工程上常忽略Cp中的全部非对角元素,即假设Cp=diag(Cp1,Cp2,…,Cpn),这时式(9)已解耦,其中的第i个方程为
(10)
式(10)两端除以Mpi,并令Cpi/Mpi=2ζiωi,可进一步得到
(11)
其中,ζi为第i阶模态阻尼比,ωi为第i阶固有圆频率。这种处理方法往往可以得到较好的近似解。
根据单自由度系统振动理论,式(11)的解为
ηi(t)=
(12)

对于冲击问题,冲击载荷作用时间很短,若只关心冲击波产生后的传播和衰减问题,则式(12)可以写成
ηi(t)=e-ζiωit·
e-ζiωitAisin(ωdit+φi)
(13)
式中:t0为冲击结束的时刻,也即为冲击波传播和衰减的初始时刻,Ai为第i阶模态振幅,φi为第i阶振动相位。
将式(13)代入式(8),得到第j个自由度位移的表达式为
(14)
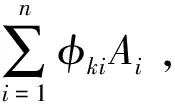
(15)
在高频激励下,系统模态密集,一般可以假定模态振型为1,并取该频段中间频率f作为系统固有频率、平均品质因子Q作为系统品质因子来近似处理,这样多自由度系统就具有了单一的固有频率和模态阻尼,从而将式(15)与式(6)统一起来。
2.2 几何扩散因子
地震学中的几何扩散因子表达式(5)存在奇点问题,即当d<1时Gij(d)>1、d趋于零时Gij(d)趋于无穷大,这显然是不合理的。由于地震学研究的尺度比较大,一般有d≫1,故该问题不影响式(5)在地震学中的使用,但不能将式(5)直接应用于航天器火工冲击问题。

对于一维问题,由于冲击波能量不存在几何扩散,有E(d2)=E(d1),故一维问题的几何扩散因子可写成
G1D=1
(16)
对于二维问题,假设冲击波能量集中在以冲击源中心为圆心、以传播距离为半径的圆弧上,则二维问题的几何扩散因子可写成
(17)
对于三维问题,假设冲击波能量集中在以冲击源中心为球心、以传播距离为半径的球面上,则三维问题的几何扩散因子可写成
(18)
2.3 CAST rule外推公式
综合上述的推导,将冲击环境数据外推公式整理如下:
(19)
式(19)可称为CAST rule,与基于试验数据拟合的NASA rule和ESTEC rule相比,理论上具有更广的适用范围,但其使用起来也略为复杂,需要额外地确定问题的维数、冲击波的传播速度v和介质的品质因子Q。
航天器结构构型中最为常见的是板壳结构,其次是梁式或桁架结构,而实体结构用的最少,它们依次对应着二维问题、一维问题和三维问题。
根据弹性力学理论,在弹性介质中存在着两种以不同速度传播的波,其中不引起旋转的波以速度vp传播,这种波称为无旋波或膨胀波,也称为纵波;不引起体积变化的波以速度vs传播,这种波称为等体积波或畸变波,也称为横波。它们的速度表达式分别为[20]:
(20)
(21)
其中,ρ为密度,λ为第一拉梅常数,G为第二拉梅常数或剪切模量。λ和G与弹性模量E和泊松比ν的关系为
(22)
(23)
将式(22)和式(23)代入式(20)和式(21),得到
(24)
(25)

介质的品质因子Q反映了介质的阻尼特性,一般需要通过试验确定,地震学中有大量的文献[17-18,21-22]研究Q值的估算方法和变化规律,可见Q值的确定具有一定复杂性。在缺少试验数据的情况下,可暂定Q=10。
3 对比分析
本节以大量的火工装置爆炸冲击试验数据为参照,对比分析CAST rule、ESTEC rule和NASA rule的预示精度,以下列出几个对比案例。
3.1 月球探测器案例一
某月球探测器相机转台解锁,参考点d1=0.15 m,预测点d2=1.45 m,所在结构板表面材料参数为:E=70 GPa、ρ=2780 kg/m3、ν=0.33;那么由三种外推公式计算出的预示曲线与试验曲线对比如图4和图5所示。
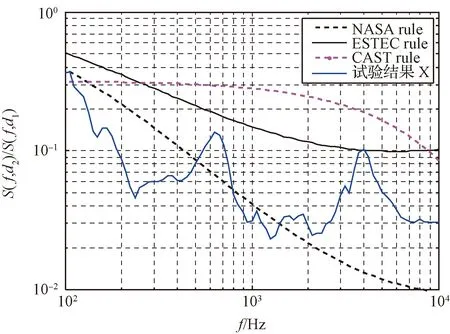
图4 预测点与参考点冲击谱比值预示曲线与试验曲线的对比示例(法向)Fig.4 Example of validation of CAST rule by comparison with actual test and comparison against NASA rule and ESTEC rule (normal)
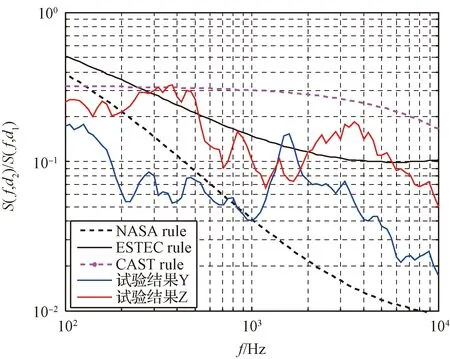
图5 预测点与参考点冲击谱比值预示曲线与试验曲线的对比示例(切向)Fig.5 Example of validation of CAST rule by comparison with actual test and comparison against NASA rule and ESTEC rule (tangential)
3.2 月球探测器案例二
某月球探测器采样机构解锁,参考点d1=0.18 m,预测点d2=1.1m,所在结构板表面材料参数为:E=70 GPa、ρ=2780 kg/m3、ν=0.33;那么由三种外推公式计算出的预示曲线与试验曲线对比如图6和图7所示。

图6 预测点与参考点冲击谱比值预示曲线与试验曲线的对比示例(法向)Fig.6 Example of validation of CAST rule by comparison with actual test and comparison against NASA rule and ESTEC rule (normal)
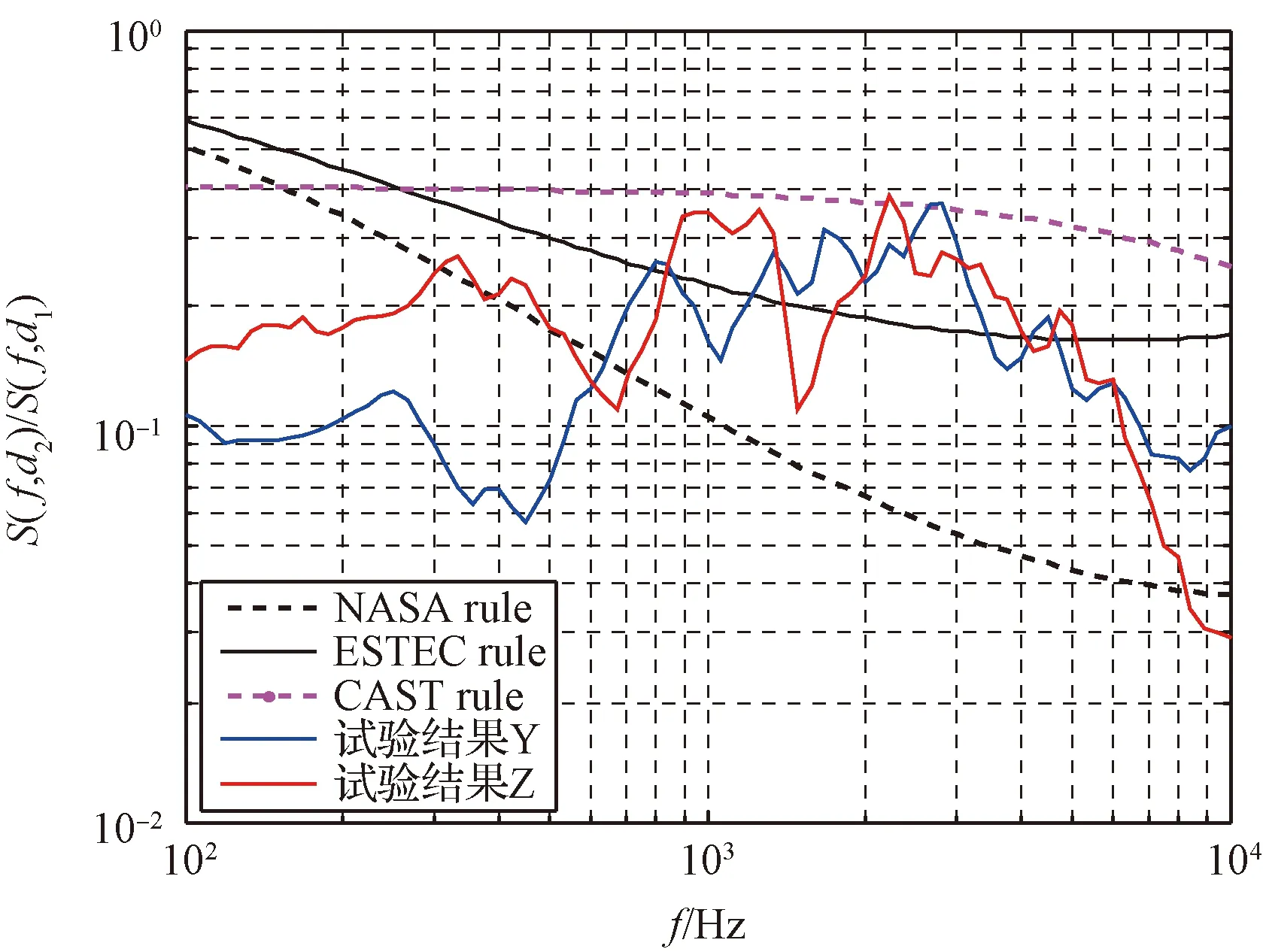
图7 预测点与参考点冲击谱比值预示曲线与试验曲线的对比示例(切向)Fig.7 Example of validation of CAST rule by comparison with actual test and comparison against NASA rule and ESTEC rule (tangential)
3.3 ESA-ESTEC案例
对于如图3所示的ESA-ESTEC案例,已知d=1.4 m。假设d1=0.1 m,d2=1.5 m,结构板表面材料参数为:E=70 GPa,ρ=2780 kg/m3,ν=0.33,则可将CAST rule预示曲线叠加在图中,如图8所示。
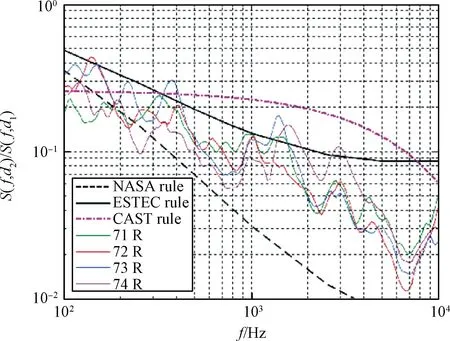
图8 ESA-ESTEC案例冲击响应预示曲线与试验曲线的对比示例Fig.8 Example of validation of CAST rule by comparison with actual test and comparison against NASA rule and ESTEC rule (ESA-ESTEC case)
3.4 小结
综合上述对比分析可知,NASA rule在中高频段的预示响应普遍比实测响应低,ESTEC rule在全频段的预示精度上优于NASA rule,但在中高频段仍常见实测响应超过ESTEC rule预示响应的情况;而CAST rule对中高频响应的包络性优于ESTEC rule,只有少数实测响应由于局部频率共振放大等原因能超过CAST rule的预示响应。
火工冲击能量主要集中在中高频段,因此该频段是火工冲击环境预示最为重要的频段。CAST rule相对于另外两个外推公式在中高频段上具有最好的预示精度,并且在理论上具有更宽的适用范围。
在上述对比分析案例中,CAST rule外推公式中介质的品质因子均取为Q=10。在获得实测响应数据之后,实际上可以通过修正Q在不同频率上的取值来实现CAST rule外推公式计算曲线与实测曲线的贴合;但是在瞬态冲击过程中Q值随频率的变化关系非常复杂,对于不同的结构、不同的位置甚至不同的振幅[23-24]都不相同,所以这种做法很难达到通用的预示效果。因此,在使用CAST rule外推公式进行冲击环境预示时仍建议取Q=10。
4 应用案例
某月球探测器在火工品起爆解锁试验中未测量分离电连接器安装处的冲击响应,试验后为了制定分离电连接器的冲击试验条件,采用上述数据外推公式根据距离较近测点的冲击响应测量数据来推算该处的冲击环境。距离分离电连接器安装位置较近的测点ZW17的最大冲击响应曲线如图9所示,该测点与冲击源的距离约为d1=0.1 m,分离电连接器安装位置与冲击源的距离约为d2=1.0 m,所在结构板表面材料参数取为E=320 GPa、ρ=1640 kg/m3、ν=0.3。根据数据外推公式计算,分离电连接器安装位置处的冲击环境预示曲线如图10所示。可见,由CAST rule外推公式计算的预示曲线峰值最高,在此基础上按照标准规定[2]增加一定余量制定出分离电连接器的冲击试验条件。

图9 距离分离电连接器安装位置较近测点ZW17的最大冲击响应曲线Fig.9 Shock response spectrum envelope of measuring point ZW17 which is relatively close to the separable electric connector

图10 分离电连接器的冲击环境推算和试验条件制定Fig.10 Extrapolation of pyroshock environments and design of test specification for the separable electric connector
5 结 论
本文综述了航天器火工冲击环境预示的三种方法,对其中数据外推法的国内外研究进展进行了详细总结和分析,并在此基础上提出了新的数据外推公式。通过理论推导和对比分析,证明本文提出的CAST rule外推公式比NASA rule和ESTEC rule外推公式有更好的通用性和预示效果,适用于航天器火工冲击环境中高频响应特性预示和组件冲击试验条件制定。
