弱引力下小行星动量驱动机器人的可控跳跃行为
2021-06-25王云飞张景瑞
王云飞,张 尧,李 谋,张景瑞
(北京理工大学宇航学院,北京 100081)
0 引 言
ESA在2004年发射的“罗塞塔-菲莱”,成为世界上首颗完成彗星表面着陆探测任务的探测器[1]。JAXA发射的“隼鸟2号”于2018年9月21日在小行星龙宫表面完成了两个MINERVA探测器的部署[2]。该探测器以跳跃的方式在小行星表面运动,跳跃距离远,可以在较短的工作寿命内完成对小行星表面较大范围的探测,能有效克服弱引力和复杂地表带来的一系列问题,但该探测器的跳跃距离和腾空高度是不可控的。借鉴成功经验,本文提出一种可控性强的动量驱动机器人(Momentum-driven Robot, MoRo),并对其动力学和控制问题开展研究。
在MoRo类型机器人的动力学建模和控制方面,学者们展开了丰富的研究。如Gajamohan等考虑动量轮和单摆两铰接点处的摩擦力,建立了倒立摆系统的非线性动力学模型,利用最小二乘法拟合系统摩擦系数等常值参数[3]。随后Gajamohan等设计了一种立方体机构(Cubli),其三个面上装有反作用飞轮,针对该Cubli机构Gajamohan等基于Kane方程建立了非线性动力学模型,通过LQR方法完成了反馈控制器的设计实现了Cubli机构的角稳定[4]。Muehlebach等使用拉格朗日方程建立了Cubli系统的非线性动力学模型并基于启发算法设计了偏移校正滤波器以降低建模过程中的误差,采用线性PID控制方法对Cubli进行角稳定控制[5]。Hockman设计了一款面向小行星探测活动的探测器,基于能量方法建立了系统动力学方程,针对跳跃、滚动和扭动三种运动形态提出了不同控制策略[6]。以上文献,虽建立了系统的动力学模型,但通常忽略了动量轮内部的摩擦,以及伺服系统非线性对系统模型的影响。因此,如何采用行之有效的方法建立完整描述MoRo类型机器人的跳跃行为动力学模型,是研究此类系统需要解决的问题。
在小行星探测任务中需要机器人有足够高的自适应能力,以实现在弱引力场以及在小行星表面环境不确定条件下的精确移动。若要实现此功能,需建立精确的行星环境模型或使用智能化方法进行辨识,学者们围绕此问题也展开了针对性的研究。如崔平远等[7]提出了一种障碍提取算法,可对着陆表面的岩石、弹坑等障碍进行信息提取,以确定最大无障碍着陆圆,降低了着陆的危险性;徐青等[8]提出了一种立体视觉在线测绘小行星形貌的方法和基于等值线分析的撞击坑特征提取方法,但其精度会随独立模型连接过程而降低,影响到小行星探测器导航与定位;So等[9]研究了基于光流的小天体表面跳跃式探测器相对定位的方法,随后引入了多相机系统,采用视觉测程法估计探测器的运动状态,解决了景深精度有限和探测器姿态变化带来的困难;郭林杰[10]在跳跃式小行星探测器的研究中结合深度确定性梯度算法进行了神经网络和奖赏函数的设计,使神经网络能够较好地学习飞轮卸载规划策略;陈康[11]通过引入价值迭代网络,使网络学习到的策略具有一定的避障能力,并针对跳跃移动任务设计了合理的单步奖赏值,加速了训练过程;Cheng等[12]为了提高小行星着陆的自主性和可靠性,提出了深度神经网络(Deep Neural Networks,DNN),为解决无小行星传递的间接方法提供了良好的初始解,并且通过解连续过程获得了精确的着陆解,实现了较高的着陆成功率;左国玉等[13]采用双质量弹簧负载倒立摆模型(Spring-loaded inverted pendulum,SLIP)对袋鼠机器人的结构进行简化,提出了通过调节着地角度控制SLIP的前进速度和通过能量补偿控制腾空高度的方法。
综上所述,目前对MoRo类型机器人的跳跃运动控制还没有成熟的研究。本文首先着眼于MoRo的结构特性,设计了MoRo的起跳过程,并分析了MoRo的跳跃机理;其次,建立了较为完善的跳跃行为动力学模型,并设计了有限时间微分控制器,解决了电机角速度的微分膨胀问题;然后,通过多次试跳辨识环境参数,并利用机器学习算法获得环境参数与跳跃参数之间的函数关系;最后,根据任务,完成对MoRo运动的控制和轨迹规划,并通过数值仿真验证了方法的可行性。
1 MoRo的跳跃行为动力学建模
1.1 MoRo的跳跃机理分析
动量驱动机器人的示意图如图1所示。MoRo为球台形对称结构,球台两侧各分布了八个触角,触角末端使用柔性部件以缓冲机器人跳跃、碰撞过程中小行星表面对其本体结构的振动冲击;内部正交布置的三个动量轮作为机器人的驱动系统,通过电机控制产生跳跃、姿态控制过程中所需要的控制力矩。
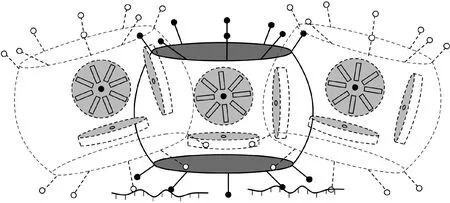
图1 MoRo示意图Fig.1 Schematic diagram of MoRo
在弱引力环境下,MoRo的跳跃原理如图2所示,当MoRo的动量轮完成减速刹车操作后,会施加给MoRo本体一个反作用力矩Tm。在该力矩Tm作用下,MoRo将会有向前翻滚运动的趋势,这会使接触触角与小行星接触表面的弹性形变增大,MoRo获得的支持力Fn将增大。当MoRo受到的支持力Fn的竖直分量大于重力G后,MoRo将产生竖直向上的加速度使触角离开小行星表面,这为MoRo完成起跳动作提供了可能。

图2 跳跃机理分析示意图Fig.2 Schematic diagram of jumping mechanism analysis

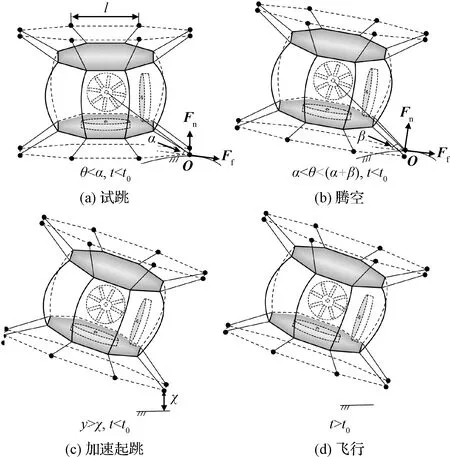
图3 MoRo起跳过程Fig.3 Jumping process of MoRo

1.2 MoRo的跳跃行为动力学模型
考虑接触碰撞、摩擦、弱引力场特性等因素,基于牛顿欧拉方法建立MoRo完整的跳跃行为动力学模型。首先,建立如图4所示的坐标系:小行星惯性坐标系fe(Oexeyeze)、MoRo本体坐标系fu(Ouxuyuzu)、动量轮安装坐标系fd(Odxdydzd)、动量轮旋转坐标系fw(Owxwywzw)。

图4 MoRo坐标系示意图Fig.4 Schematic diagram of coordinate system of MoRo
定义A21是坐标系1到坐标系2的坐标转换矩阵;r12是f1系下从点1到点2的矢量列阵;r×是矢量列阵r的叉乘矩阵。第i个动量轮上的质量元dmwi和本体上的质量元dm的矢径Rwi,R表述在fu下为:
(1)
式中:ru,rwi是质量元dm,dmwi在fu,fw下的矢量列阵。
不考虑动量轮动静不平衡的影响,第i个动量轮和本体的动量Pwi,Pu表述在fu下为:
(2)
式中:m是本体的质量;mwi是第i个动量轮的质量;vd是MoRo质心速度的矢量列阵;Su是MoRo本体对其体坐标系的静矩。
第i个动量轮、MoRo本体相对于MoRo质心Ou的动量矩表述在fu下为:
(3)
式中:Iwi,Id分别为第i个动量轮、MoRo本体的转动惯量;Ωi是第i个动量轮转速的矢量列阵。
起跳过程中小行星表面会施加给MoRo切向摩擦力Ff,需要建立碰撞过程中的切向摩擦力模型。借助于Karnopp模型方法,得到切向摩擦力Ff的计算公式为[14]:
(4)
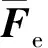
碰撞过程中,接触碰撞点的法向接触力可以描述为[15-16]:
(5)
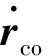
小天体质量体积比较小,形状不规则这导致其附近呈现不规则的弱引力场[17]。将形状、质量不规则的小行星简化为椭球体,利用球谐系数法对其展开,可得到目标小行星的引力势函数为:
(6)
式中:Pn,m(sinφ)为缔合勒让德多项式;Cn,m和Sn,m为引力场模型的球谐系数;θ是探测器着陆点的经度;φ是探测器着陆点的纬度;n为引力场模型的阶数;m为引力场模型的次数、R0为目标小行星的参考半径;R为探测器到小行星质心的距离;G是万有引力常量。
MoRo受到的引力加速度g是引力势函数U的梯度,可表示为:
g=gradU
(7)
引力势函数的梯度是引力势函数各变量求偏导数,本文取其前二阶来近似引力势函数[18]:
(8)
根据动量矩定理,整理可得到表述在坐标系fu下MoRo的转动动力学方程为:
(9)
式中:ruf1是MoRo质心与接触碰撞点连接矢径的矢量列阵;ruf2是MoRo质心与重心连接矢径的矢量列阵;Fn和Ff是支持力和摩擦力的矢量列阵;G是MoRo受到的重力的矢量列阵。
根据动量定理,整理得到描述在坐标系fu下MoRo的平动动力学方程为
(10)
将所建立的Karnopp摩擦模型式(4)、连续接触力Hertz模型式(5)、引力场模型式(8)代入到式(9)、式(10)中即可得到MoRo的跳跃行为动力学模型。
1.3 三闭环伺服系统和有限时间收敛微分器
利用永磁同步电机实现对动量轮的精确控制使MoRo完成跳跃动作以及姿态控制等任务[19]。采用id=0的矢量控制策略,该策略所需的定子电流最小且损耗低。仅考虑摩擦非线性对系统的影响,使用LuGre摩擦模型描述该非线性特性。LuGre摩擦模型可表示为[20]:
(11)

结合系统特点,基于奇异摄动技术,设计有限时间收敛微分器以保证电机伺服系统的微分精度[21]
(12)
2 环境参数辨识和跳跃参数设计
2.1 辨识环境参数
通过训练BP神经网络并分析MoRo多次起跳数值仿真的结果,找到环境参数K、C与试跳阶段结束时的速度大小V、速度与水平面之间的夹角η、高度h之间的函数关系,即:
(K,C)=ζ(V,η,h)
(13)
给定K的取值范围为100000~200000 N/m3/2,C的取值范围为100~200 N/(m·s-1)。将K和C排列组合代入式(9)、式(10)中,得到MoRo试跳结束时与K,C相对应的V、η和h的大量数据。剔除MoRo跳跃两次以上的数据、因参数不当跳跃距离和腾空高度过小的数据后,使用该数据训练神经网络得到式(13)中K、C与V,η和h之间的关系。为验证估计环境参数的精度,选取30组测试数据。环境参数的估计值和实际值如图5、图6所示。

图5 K的估计值和实际值Fig.5 Estimated and actual values of K
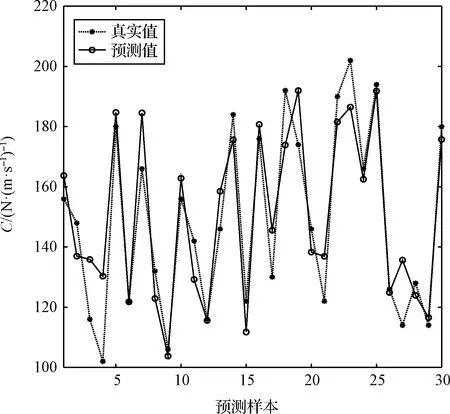
图6 C的估计值和实际值Fig.6 Estimated and actual values of C
2.2 设计跳跃参数
辨识环境参数后,通过训练BP神经网络设计跳跃参数,使MoRo每跳跃一次就可得到期望的腾空高度和跳跃距离。调整MoRo在起跳过程中的跳跃参数Te、α和β,得到腾空高度H和跳跃距离L。通过动量分配实现从起点到终点的多次跳跃,使腾空高度、跳跃距离可控。在环境参数K、C已知的情况下,建立跳跃参数和跳跃轨迹参数之间的关系,即Te、α和β与H,L之间的函数关系如下:
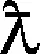
(14)
给定α的取值范围为40°~60°,β的取值范围为20°~40°,将α和β排列组合代入式(9)、式(10)中,得到与α,β相对应的H,L的值,实际起跳过程中Te可预先设定为定值。使用得到的大量数据训练神经网络得到式(14)中H、L与α、β和Te之间的关系,该学习结果作为MoRo起跳角α、腾空角β选取的依据。选取30组测试数据,H和L的估计值和实际值如图7、图8所示。
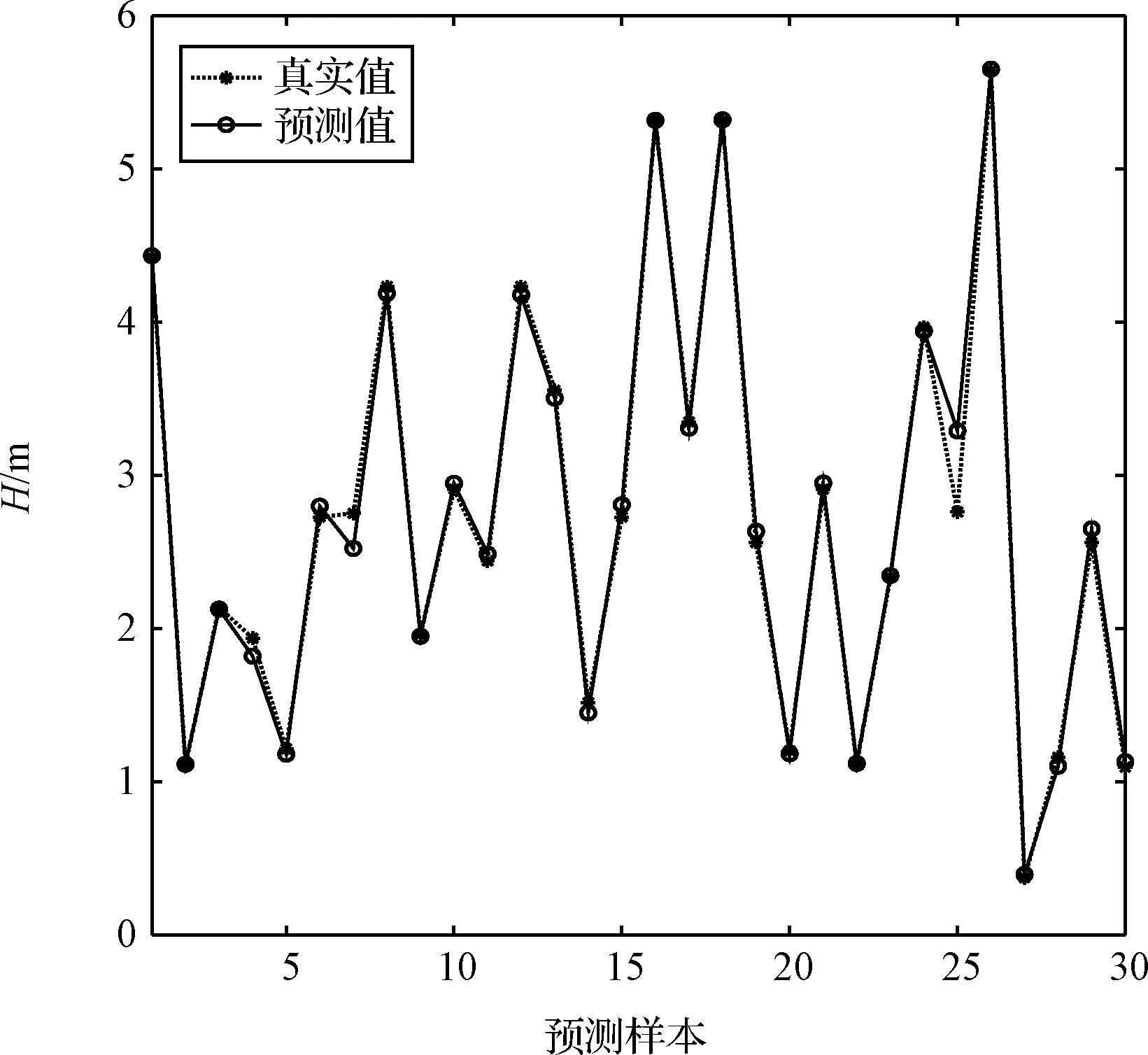
图7 H的估计值和实际值Fig.7 Estimated and actual values of H

图8 L的估计值和实际值Fig.8 Estimated and actual values of L
定义相对估计误差λ为:
(15)
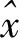
根据式(15)可得到相对估计误差。剔除极个别有较大偏差的预测样本,环境参数相对估计误差和腾空高度和跳跃距离相对估计误差均在15%以内。
3 仿真校验
弱引力环境下,给定目的地点B点坐标为(20.5,-17.5) m,在x-y平面上,MoRo从出发点A经过若干次试跳辨识其所在的环境参数并选取合适的跳跃参数到达目的地点B。给定环境参数的值为K=119000 N/m3/2,C=106 N/(m·s-1),经过若干次试跳通过机器学习算法辨识得到的环境参数的值为K=104702 N/m3/2,C=103.8 N/(m·s-1)。仿真过程中认为MoRo本体的几何形状是正八棱柱,其它主要参数见表1。

表1 其他主要参数Table 1 Other main parameters
表2是MoRo辨识环境参数后,完成起跳动作选取的跳跃控制器参数和实际的跳跃轨迹参数。MoRo最终经过四次跳跃到达目的地点B,数字1,2,3,4是MoRo四次跳跃的跳跃次序。给定MoRo四次跳跃的理想起跳点坐标、理想最高点坐标和理想落地点坐标。单次起跳后的理想跳跃轨迹由理想跳跃最高点所在z轴为对称轴,分别经过理想起跳点和理想落地点的两段抛物线组成。图9为MoRo的理想运动轨迹与实际运动轨迹,图中分别标记了理想曲线和实际曲线以及每次跳跃的起始点、最高点和落地点。实际到达目的地点B的x-y坐标为(20.5404,-17.2605) m。
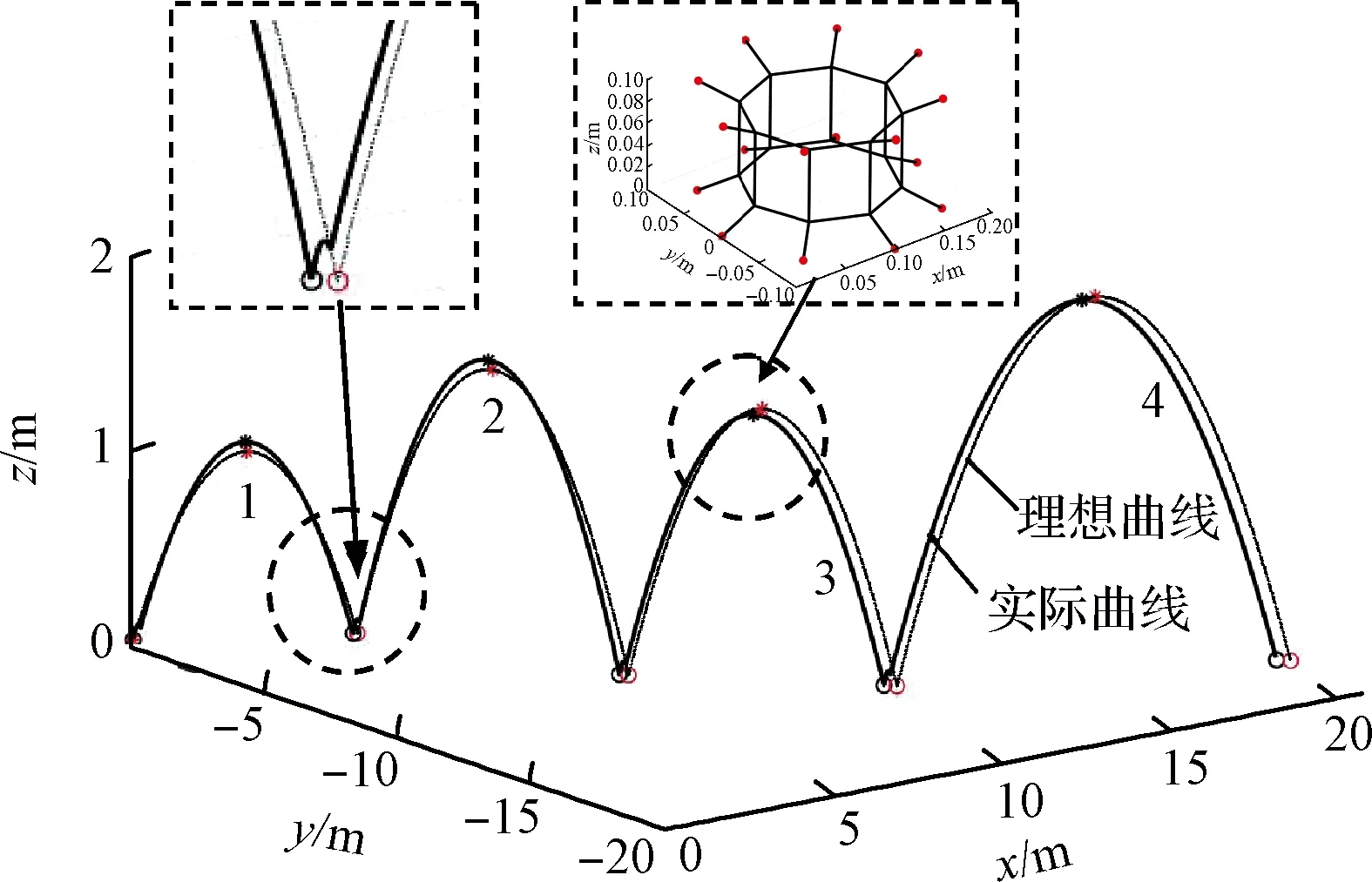
图9 MoRo的理想运动轨迹和实际运动轨迹Fig.9 Ideal trajectory and actual trajectory of MoRo

表2 跳跃控制器参数与跳跃轨迹参数Table 2 Jumping controller parameters and jumping trajectory parameters
MoRo的姿态使用欧拉角描述,MoRo每次起跳后在空中保持某一特定姿态执行定点拍照任务。三个动量轮分别独立控制俯仰轴、偏航轴和滚动轴的姿态,其姿态控制律具有相似性,其中一个动量轮控
制的偏航轴方向的姿态力矩Tca为:
(16)
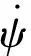
图10是MoRo连续跳跃过程中偏航角速度误差和偏航角误差。四次跳跃给定的偏航角分别为42°、144°、85°和113°,由于MoRo在落地瞬间会受到较大的冲击,会导致MoRo的姿态角速度发生突变,该突变持续时间在0.1 s左右,直至MoRo平稳着地后消失。由图10可知,MoRo的偏航角误差控制在0.5°以内。

图10 偏航角和偏航角速度的误差值Fig.10 Error value of yaw angle and yaw rate
图11是MoRo四次跳跃的过程中受到的Hertz力Fn和Karnopp力Ff的大小,MoRo通过在跳跃瞬间获得小行星表面的碰撞力和与小行星表面接触产生的摩擦力完成起跳。
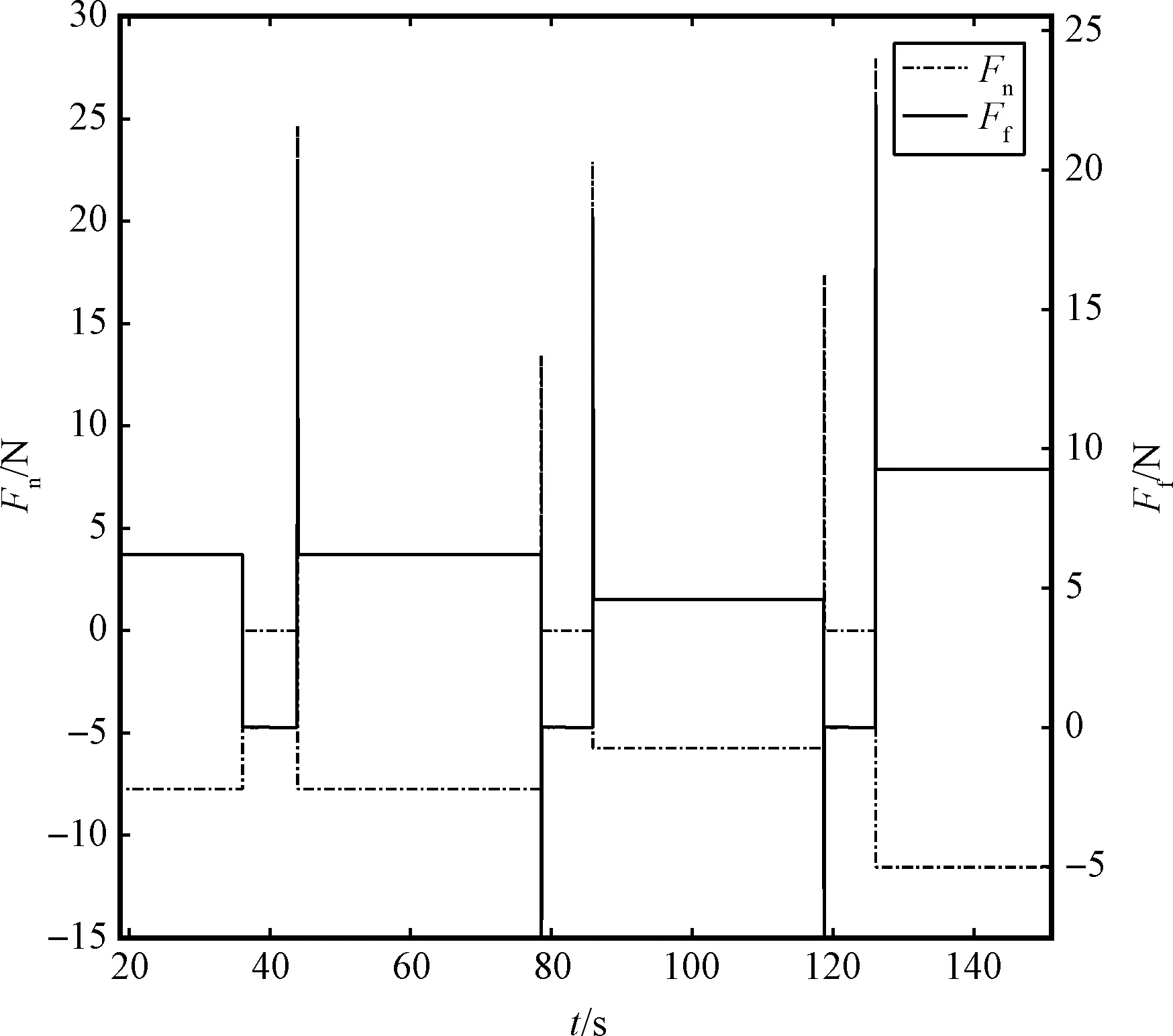
图11 连续跳跃过程中MoRo受到的Hertz力和Karnopp力Fig.11 The Hertz and Karnopp forces acting on the MoRo during continuous jumping
表3、表4分别为四次跳跃最高点和落地点的期望坐标、实际坐标以及误差,其中误差定义为期望点与实际点间的距离。误差有逐渐增大的趋势,原因在于MoRo每次跳跃结束后不能精确到达落地点,导致再跳跃时起跳点不能与理想起跳点重合。由表3、表4可知,MoRo跳跃最高点的误差在0.2 m以内,落地误差在0.35 m以内。

表3 跳跃最高点的期望坐标、实际坐标和误差Table 3 The expected coordinates, actual coordinates and errors of the highest point

表4 跳跃落地点的期望坐标、实际坐标和误差Table 4 The expected coordinates, actual coordinates and errors of point of fall
4 结 论
本文提出了一种小行星表面弹跳运动可控的动量驱动机器人。考虑接触碰撞摩擦、弱引力场、电机特性等因素建立了该机器人的跳跃行为动力学模型,可为数值仿真提供理论模型并能完整描述MoRo的跳跃运动过程;提出基于BP神经网络的环境参数辨识和跳跃参数设计方法,该方法可以达到使MoRo的跳跃距离、腾空高度可控的效果;通过数值仿真分析,MoRo的落地点精度可达到0.35 m以内,跳跃最高点精度可在0.2 m以内,姿态稳定精度在0.5°以内,验证了方法的可行性及有效性。
