某小型客车车身骨架轻量化综合优化设计

于保君， 何洪军， 肖永富， 杨少明， 孙立伟， 董 健

(中国第一汽车股份有限公司 研发总院，汽车振动噪声与安全控制综合技术国家重点实验室， 长春 130012)

汽车轻量化可以起到节能减排、保护环境的作用。汽车质量每减小100 kg,每升汽油可多行驶1 km[1]。客车车身质量占客车总质量的 40%～60%[2]。因此，车身轻量化工作极其重要。目前，车身结构轻量化方法主要包括拓扑优化、截面优化、厚度优化等。

目前，客车骨架结构优化一般仅采用一种方法[3-8]，未见综合利用拓扑优化、截面及厚度优化方法；针对客车骨架型材截面尺寸优化，一般采用一维梁单元模型，未见利用二维壳单元模型。本文建立某小型客车车身骨架隐式参数化模型，确认参数化模型精度满足技术要求后，对其侧围骨架进行拓扑优化，寻求局部最优结构；然后基于拓扑优化的壳单元模型，对车身骨架型材的截面尺寸和厚度同时优化，并进行强度校核。最终在满足刚度、强度及模态指标要求前提下，其车身骨架实现减重26.7 kg。

1 小型客车车身骨架轻量化路线

某小型客车车身骨架是由不同截面的矩管铝型材拼焊而成的空间桁架结构，长4 372 mm，宽1 864 mm，高2 115 mm。由于传统有限元模型无法实现型材截面尺寸参数化变更，显式参数化有限元模型虽然可以通过移动网格节点坐标实现截面尺寸变更，但很难实现截面尺寸较大变更和结构间复杂连接关系的更新；而隐式参数化有限元模型可以使用基点位置、基线曲率和截面形状等参数来控制型材截面尺寸及形状，并通过映射关系建立零部件结构之间的参数化装配关系，每一个参数的改变都会使它周边与之关联的结构或零部件参数发生相应变化，保证了其连接关系的稳定性和模型整体的连续性[9-12]。

另外，由于隐式参数化有限元模型在建模过程中简化了圆角、孔和加强筋等局部几何特征，而传统有限元模型对实际结构简化较少，更接近实际情况。因此，该小型客车骨架轻量化设计路线如图1所示。首先，建立该小型客车的传统有限元模型作为确认标准，然后再建立该客车的隐式参数化有限元模型，并计算两种有限元模型的部分性能值予以对比，以确认隐式参数化有限元模型的精度。再基于隐式参数化有限元模型开展车身局部结构拓扑优化、型材截面和厚度优化，以降低车身重量；最后校核整车结构强度，确定轻量化方案。

图1 某小型客车车身骨架轻量化设计路线

2 某小型客车车身结构轻量化设计

2.1 隐式参数化模型建模及性能计算

该小型客车车身骨架传统有限元模型采用壳单元划分网格，单元尺寸5 mm，采用单元共节点方式模拟焊接。整车传统有限元模型壳单元342 004个，节点335 881个。

使用SFE.Concept软件建立该客车骨架的隐式参数化有限元模型，步骤如下：在SFE.Concept软件中，以车身局部结构为例，如图2所示。选定梁的端点定义基点1和2，连接基点1和2，形成基线1，根据型材的空间走向，调整基线的曲率；依据型材结构定义截面1和3；通过上述基点、基线及截面定义①号型材，由于①号型材为弯曲件，需在中间增加截面2，保证①号型材在弯曲处与原结构相同。②号型材定义同①号型材，再将①号型材与②号型材的焊接边进行映射，以保证①号型材与②号型材连接关系。参数化结构搭建完成后，再利用SFE.Concept软件自动生成网格功能，完成①、②号型材隐式参数化有限元模型的建立。通过控制基点、基线或者截面实现结构变化，结构变化后重新生成新结构的有限元网格。

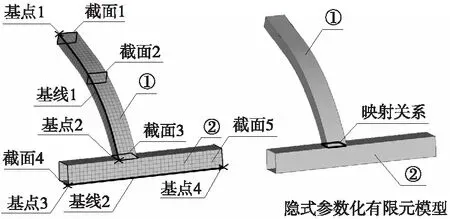
图2 隐式参数化有限元模型建立示意图

应用上述方法搭建的该小型客车车身骨架隐式参数化模型包括573个基点、356 根基线、1 320个基础截面、356根梁和705组映射关系。网格化后的参数化有限元模型含壳单元337 256个(壳单元尺寸5 mm)，节点331 173个。整车骨架隐式参数化有限元模型如图3所示。

图3 车身骨架参数化有限元模型示意图

弯曲刚度、扭转刚度、一阶扭转模态频率、重量是评价小型客车身骨架的关键性能指标。该参数化有限元模型与传统有限元模型的这些指标的计算结果见表1。可以看出，相对于传统有限元模型，参数化有限元模型的误差≤1%，满足后续分析要求。

2.2 侧围局部拓扑优化

考虑到装配、布置限制，本文选取受限小的左侧围结构进行局部拓扑优化。考虑地板与侧围结构限制关系，确定优化区域如图4所示。

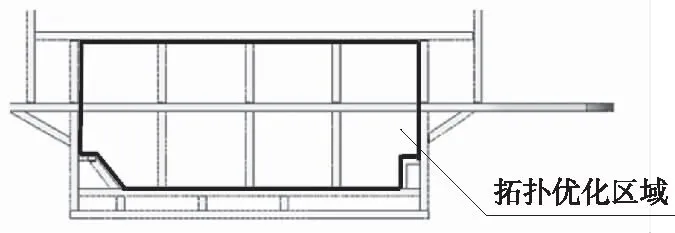
图4 侧围拓扑优化设计区域

为避免多目标优化时弯曲刚度、扭转刚度、一阶扭转模态频率权重系数分配的不合理，依据工程实际要求，采用单目标多约束优化方式求解满足扭转刚度、弯曲刚度、一阶扭转模态频率要求的最轻结构，即构建的优化模型如下：

Findρ=(ρ1,ρ2…ρn)

minMass

s.t.

KT(ρ)≥13 500 N·m/(°)

Kb(ρ)≥12 000 N/mm

ω(ρ)≥23 Hz

0<ρmin≤ρi≤1

式中：ρ=ρ1,ρ2…ρn是设计变量密度；n为单元数；Mass为车身骨架质量；KT为车身骨架扭转刚度；Kb为车身骨架弯曲刚度；ω为车身骨架一阶扭转模态频率。

综合考虑型材规格、焊接工艺、附件安装等限制，侧围拓扑优化后工程结构设计如图5所示。拓扑优化后，车身骨架扭转刚度提升2.6%；弯曲刚度下降1.6%，但仍满足要求，一阶扭转模态频率提升7.6%；质量降低7.7 kg。

图5 侧围拓扑优化结果及工程结构设计

2.3 车身骨架型材截面及壁厚优化

基于拓扑优化结构，选取车身骨架型材截面及厚度作为优化变量；仍以前述的扭转刚度、弯曲刚度和一阶扭转模态频率要求为约束条件，目标为小型客车身骨架重量最轻。

2.3.1 变量选取

小型客车身骨架主要由矩形管型材拼焊而成，其截面如图6所示。为避免局部结构应力集中，通常搭接2根型材在某一方向上等尺寸，图6中④方案搭接为最佳方案(2个型材截面高度一致，都为50 mm)。

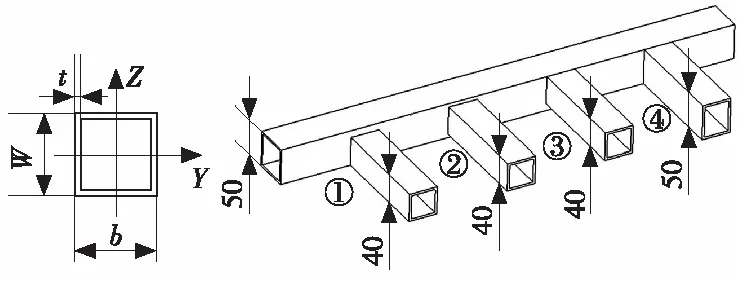
图6 型材截面及搭接关系示意图

从车身骨架中选取99根型材，考虑型材位置与规格，将该99根型材分成23组，如图7所示。考虑相邻型材之间截面尺寸单方向的一致性，将型材高度w或宽度b作为截面优化变量，壁厚t作为厚度优化变量，合计46个变量。同时，为节约成本，不额外增加型材规格，截面和壁厚变量值根据现有型材库选取。

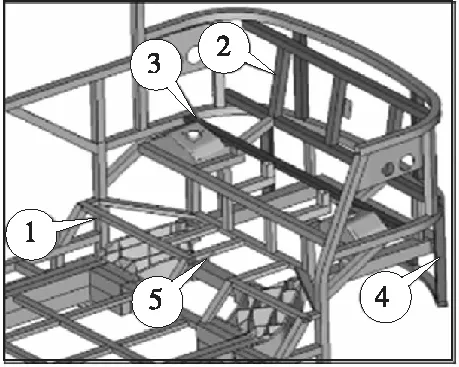
图7 变量位置示意图

2.3.2 优化流程搭建

基于响应面法搭建近似模型，通过模拟退火算法进行寻优。

首先，采用优化拉丁超立方方法生成截面尺寸和壁厚变量的试验设计样本。利用Isight软件驱动参数化模型获得样本点计算模型500个，提交给NASTRAN软件计算其扭转刚度、弯曲刚度、一阶扭转模态频率和质量。

然后，基于样本的上述刚度及模态频率和重量信息，构建响应面模型。经采用交叉验证方法进行误差分析，证明模型精度满足要求(精度要求≥0.9)，其中一阶扭转模态频率精度为0.97，其余3项精度均为0.99。

最后，采用自适应模拟退火方法，寻求刚度、模态满足要求的重量最小的截面及壁厚组合。优化模型如下：

Findvar=(s1,s2…s23,t1,t2,…t23)

minMass

s.t.

KT(var)≥13 500 N·m/(°)

Kb(var)≥12 000 N/mm

ω(var)≥23 Hz

s3,s20∈(-10,0,10)s18∈(-20,-10,0,10)

s19,s22∈(-30,-20,-10,0)

其他截面尺寸si∈(-20,-10,0)

t1,t2,…,t23∈(2,3,4)

式中：var为设计变量；s1,s2…s23为23个截面尺寸变量，t1,t2,…t23为23个壁厚尺寸变量；其余参数含义同2.2节。

2.3.3 优化结果

如图8所示，经2 568次迭代优化计算，在扭转刚度、弯曲刚度、一阶扭转模态频率性能满足要求的前提下，实现质量降低19.2 kg。将各变量优化值代入隐式参数化有限元模型生成优化后的隐式参数化有限元模型，计算其关键性能指标，结果见表2。

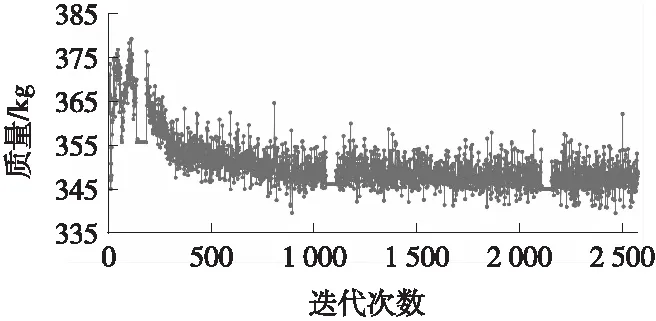
图8 小型客车骨架重量优化

表2 截面、壁厚优化的车身骨架性能指标

2.4 整车优化方案强度校核及改进

通过上述综合优化方案，车身骨架共计减重26.9 kg。将电池、内外饰件、座椅等部件重量简化为集中质量并用RBE3单元连接到该车身骨架模型中，构成小型客车全内饰有限元模型，以保证该模型总重、局部的重量分布以及质心位置与实际一致。对该内饰有限元模型再进行强度分析得知，最大应力工况是满载弯曲工况，最大应力出现在车门铰链安装处，其值为260 MPa，高于铝型材6061的屈服极限240 MPa，其他位置满足强度要求。通过在门铰链安装局部增加2 mm厚加强板增重0.2 kg，最大应力降低为137 MPa，满足强度要求。

3 结束语

本文建立小型客车车身骨架隐式参数化有限元模型，与传统有限元模型进行对比，保证了隐式参数化有限元模型的精度。以隐式参数化有限元模型为基础进行拓扑优化，同时进行截面尺寸及壁厚优化，并在已有型材库中选取型材规格。在保证扭转刚度、弯曲刚度、一阶扭转模态频率满足要求的前提下进行车身骨架轻量化、综合优化设计。后续将结合实车试验做进一步研究。