基于模糊数学理论的具有自学习功能的故障诊断系统研究
2021-06-24张秋颖沈小芳
张秋颖 沈小芳

【摘要】本文提出了一种基于模糊聚类和模糊模式识别的故障诊断系统的诊断流程,并讨论了将原始数据进行前期处理的方法,同时提出了使故障诊断系统具有自学习功能的方法.本文提出的方法不仅具有一定的学术价值,在实践中也具有指导意义.最后,本文对以上的研究工作进行了总结,并提出了进一步的研究方向.
【关键词】模糊聚类;模糊模式识别;故障诊断;自学习
引 言
基于模糊数学理论中的模糊聚类和模糊模式识别技术进行故障诊断是目前的研究热点,文献[1]研究了基于模糊聚类的柴油机故障诊断技术,其采用的是经典的模糊C均值聚类算法,该算法的一个明显缺点是以欧式距离度量样本间的距离,进而得出隶属度,仅对球状或椭球状数据集(各向同性数据集)能得出较优的分类结果,对其他类型数据集分类效果差,甚至与实际情况不符;文件[2][3]提出了改进的模糊C均值聚类故障诊断方法,即在计算样本距离时乘以一个权值;文献[4]以遗传算法计算权值,其实质仍然是以欧式距离度量样本间的距离.
结合上述介绍,本文主要研究的内容为:一是讨论基于模糊数学理论的故障诊断流程,并提出将系统原始数据集变换为各向同性数据集的思想;二是提出一种故障诊断系统的自学习机制,使故障诊断系统真正具有智能性.
一、模糊聚类、模糊模式识别与故障诊断
设对某个系统进行故障诊断,采集系统数据m个,每隔一段时间记录一组样本,已记录样本n个,分别用x1,x2,…,xn表示,其中每个样本的具体数据为:
xi=(xi1,xi2,…,xim)(i=1,2,…,n)(1)
于是可得原始数据矩阵如下表所示.
应用模糊聚类技术并结合实际情况,将上述n个样本分为r类,其中,第j类的样本数为nj,分别用x(j)1,x(j)2,…,x(j)nj表示,其中每个样本的具体数据为:
x(j)i=(x(j)i1,x(j)i2,…,x(j)im)(i=1,2,…,nj,j=1,2,…,r) (2)
第j类的聚类中心为:
x-(j)=(x-(j)1,x-(j)2,…,x-(j)m)(3)
式中x-(j)k为第k个数据的平均值,即:
x-(j)k=1nj∑nji=1x(j)ik(k=1,2,…,m)(4)
将n个样本分好类后,面对样本xn+1,根据r个聚类中心,应用模糊模式识别技术,将样本xn+1归为r类中的某类或求出其隶属于各类的隶属度.
以上即是基于模糊数学理论的故障诊断系统的基本原理,其是模糊聚类和模糊模式识别的综合运用过程.以下讨论具体故障的诊断流程.
二、基于模糊数学理论的故障诊断流程
在给出故障诊断流程之前,先讨论一下原始数据的前期处理.不同的数据一般有不同的量纲,为了使有不同量纲的量也能进行比较,需要对数据作适当的变换,通常是归一化处理,即将数据值压缩到区间[0,1]上.
应用模糊聚类进行故障诊断,需要计算样本之间的相似程度,而相似程度通常以样本间的欧式距离为基础.这就存在一个问题,即在某些情况下,欧式距离不能准确反映样本之间的相似程度,甚至与事实不符.
如某系统的电压、电流样本x1,x2,x3,x4分布如图1所示.从图中可以直观看出,若用欧式距离法计算样本之间的相似程度,则样本分类为{x1,x2},{x3,x4}.而实际情况中,若以系统的功率分类,则上述分类是符合事实的;若以系統表现出的电阻值分类,则符合事实的分类应为{x1,x3},{x2,x4}.
因此,若要进行符合事实的分类,在将原始数据归一化处理之前,应去除原始数据之间的耦合性,使原始数据集变换为各向同性数据集.对于图1所示的数据,以系统功率分类时,应以UI为新数据;以系统表现出的电阻值分类时,应以U/I为新数据.而实际系统复杂多样,且对同一系统,不同的分类所关心的数据也不一样,因此,并没有统一的使原始数据集变换为各向同性数据集的方法,应具体问题具体分析.本文总结出以下几种方法.
1.专家统计法
统计本领域内的专家意见,并进行综合考虑.
2.加权法
不同的分类所关心的数据不同,对分类影响大的数据给予大的权值,对分类影响小的数据给予小的权值.
3.借用法
直接借用已有的客观指标,如要将某些人按胖瘦分类,采集每人的身高、体重信息,则应采用国际通用的BMI指数(BMI=体重(kg)/身高2(m))方法进行数据变换.
4.倒推试凑法
如已事先知道样本的分类情况,可采用倒推试凑法,哪种数据变换方法的分类效果最好,就采用哪种方法.
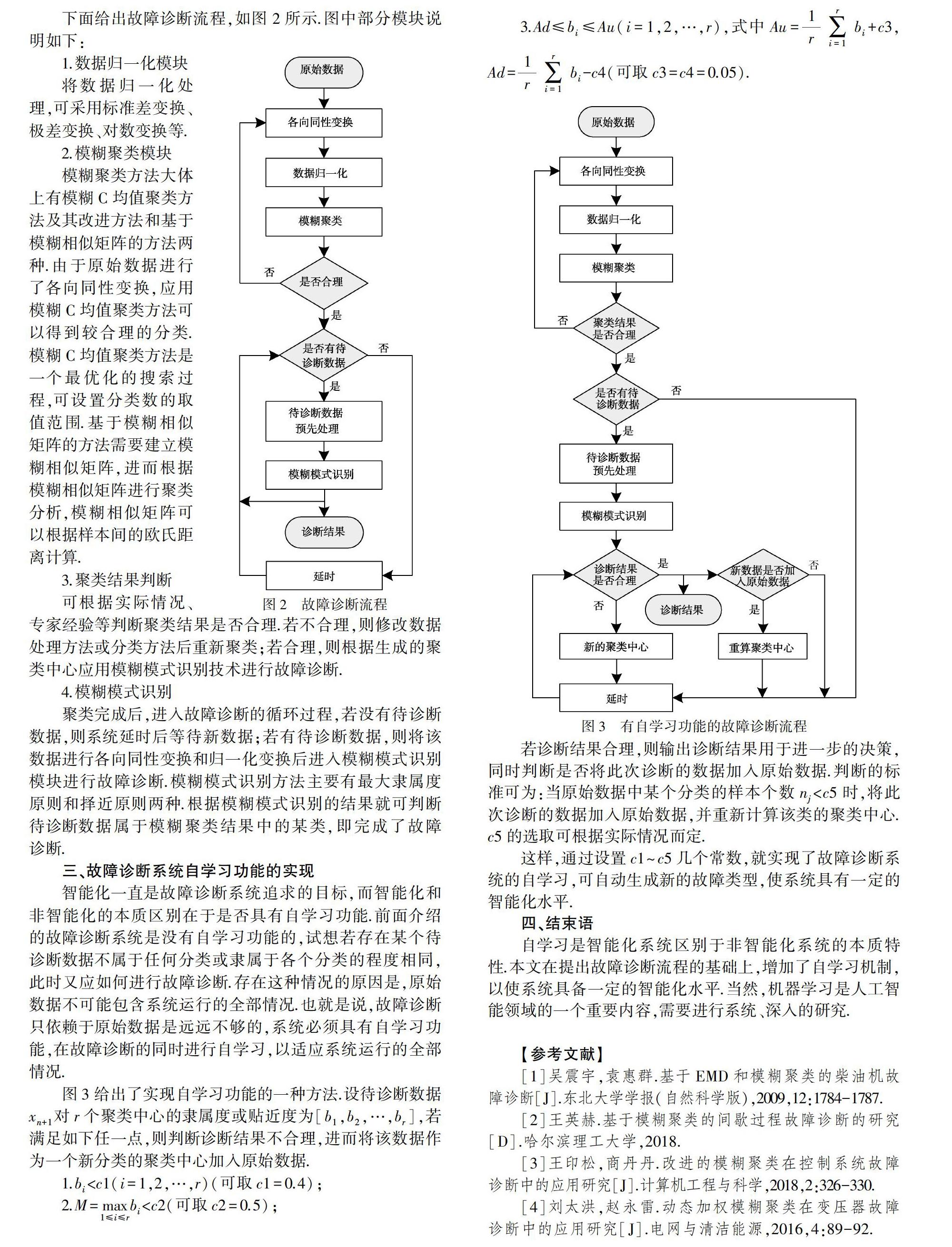
下面给出故障诊断流程,如图2所示.图中部分模块说明如下:
1.数据归一化模块
将数据归一化处理,可采用标准差变换、极差变换、对数变换等.
2.模糊聚类模块
模糊聚类方法大体上有模糊C均值聚类方法及其改进方法和基于模糊相似矩阵的方法两种.由于原始数据进行了各向同性变换,应用模糊C均值聚类方法可以得到较合理的分类.模糊C均值聚类方法是一个最优化的搜索过程,可设置分类数的取值范围.基于模糊相似矩阵的方法需要建立模糊相似矩阵,进而根据模糊相似矩阵进行聚类分析,模糊相似矩阵可以根据样本间的欧氏距离计算.
3.聚类结果判断
可根据实际情况、专家经验等判断聚类结果是否合理.若不合理,则修改数据处理方法或分类方法后重新聚类;若合理,则根据生成的聚类中心应用模糊模式识别技术进行故障诊断.
4.模糊模式识别
聚类完成后,进入故障诊断的循环过程,若没有待诊断数据,则系统延时后等待新数据;若有待诊断数据,则将该数据进行各向同性变换和归一化变换后进入模糊模式识别模块进行故障诊断.模糊模式识别方法主要有最大隶属度原则和择近原则两种.根据模糊模式识别的结果就可判断待诊断数据属于模糊聚类结果中的某类,即完成了故障诊断.
三、故障诊断系统自学习功能的实现
智能化一直是故障診断系统追求的目标,而智能化和非智能化的本质区别在于是否具有自学习功能.前面介绍的故障诊断系统是没有自学习功能的,试想若存在某个待诊断数据不属于任何分类或隶属于各个分类的程度相同,此时又应如何进行故障诊断.存在这种情况的原因是,原始数据不可能包含系统运行的全部情况.也就是说,故障诊断只依赖于原始数据是远远不够的,系统必须具有自学习功能,在故障诊断的同时进行自学习,以适应系统运行的全部情况.
图3给出了实现自学习功能的一种方法.设待诊断数据xn+1对r个聚类中心的隶属度或贴近度为[b1,b2,…,br],若满足如下任一点,则判断诊断结果不合理,进而将该数据作为一个新分类的聚类中心加入原始数据.
1.bi 2.M=max1≤i≤rbi 3.Ad≤bi≤Au(i=1,2,…,r),式中Au=1r∑ri=1bi+c3,Ad=1r∑ri=1bi-c4(可取c3=c4=0.05). 若诊断结果合理,则输出诊断结果用于进一步的决策,同时判断是否将此次诊断的数据加入原始数据.判断的标准可为:当原始数据中某个分类的样本个数nj 这样,通过设置c1~c5几个常数,就实现了故障诊断系统的自学习,可自动生成新的故障类型,使系统具有一定的智能化水平. 四、结束语 自学习是智能化系统区别于非智能化系统的本质特性.本文在提出故障诊断流程的基础上,增加了自学习机制,以使系统具备一定的智能化水平.当然,机器学习是人工智能领域的一个重要内容,需要进行系统、深入的研究. 【参考文献】 [1]吴震宇,袁惠群.基于EMD和模糊聚类的柴油机故障诊断[J].东北大学学报(自然科学版),2009,12:1784-1787. [2]王英赫.基于模糊聚类的间歇过程故障诊断的研究[D].哈尔滨理工大学,2018. [3]王印松,商丹丹.改进的模糊聚类在控制系统故障诊断中的应用研究[J].计算机工程与科学,2018,2:326-330. [4]刘太洪,赵永雷.动态加权模糊聚类在变压器故障诊断中的应用研究[J].电网与清洁能源,2016,4:89-92.
