滚子包络环面蜗杆传动副装配误差分析

2021-06-24陈永洪郑正鼎陈兵奎

重庆大学学报 2021年6期

唐鹏，陈永洪，郑正鼎，陈兵奎

(重庆大学机械传动国家重点实验室, 重庆 400044)

蜗杆传动属斜面传动，作为齿轮传动的一个重要分支，其传动原理与典型齿轮传动的杠杆传动原理有较大区别，蜗杆传动副齿面相对滑动速度较大，齿面磨损较快。

将蜗杆传动副共轭齿面之间的滑动摩擦改为滚动摩擦是减小摩擦系数提高传动效率的有效途径。Kato等[1]提出针轮蜗杆传动，并对其结构设计、加工工艺、传动效率及润滑条件等问题进行了全面的研究，日本三共(SANKYO)株式会社成功地将滚柱包络环面蜗杆传动应用于减速器生产。Siegmund等提出了滚珠环面蜗杆传动，在蜗轮与环面蜗杆之间加入了钢球作为蜗轮齿，并在钢球和蜗轮母体球窝内布满小钢珠以减小钢球与蜗轮母体之间的滑动摩擦[2]。张光辉等[3]和陈永洪等[4]提出滚锥包络环面蜗杆传动，并进行了啮合理论、参数优化、样机制造及性能试验等方面的系统研究，证明滚锥包络环面蜗杆传动具有传动效率高、承载能力大、使用寿命长及制造简单等优点。邓星桥等[5-6]提出无侧隙双滚子包络环面蜗杆传动，所用蜗杆是以蜗轮齿面为原始母面包络展成的环面蜗杆，蜗轮轮齿则是两个能够绕其自身轴线转动的滚子，不仅具有滚子包络环面传动效率高、啮合齿数多、承载能力强等优点，还具有侧隙可调及零侧隙的特点。Chen等[7]建立了球面包络环面蜗杆传动的啮合几何学，分析了误差对传动副接触区域的影响规律。Wang等[8]分析了滚子包络环面蜗杆传动副的时变啮合刚度，研究了滚子直径对啮合刚度的影响规律。Deng等[9]分析了滚子包络环面蜗杆传动减速器的润滑流场。上述对滚子包络环面蜗杆传动副的研究主要是针对蜗杆的啮合传动性能、设计参数优化、润滑流场等方面[5-9]。但是单纯在理论状态下建立的数学模型并不能反映实际工况下传动副的接触情况，缺乏装配误差对齿面接触的影响规律等理论指导，则会导致在传动过程中出现轮齿接触不良、卡死等现象。

笔者基于滚子包络环面蜗杆的传动原理，建立了考虑装配误差的传动副干涉分析模型，提出了干涉定量评价指标及其数值计算方法，并系统地分析了中心距误差、蜗杆轴向窜动量误差、滚子蜗轮轴向误差和轴交角误差对滚子包络环面蜗杆传动副的接触情况的影响规律。

1 滚子包络环面蜗杆传动副啮合几何学

1.1 几何标架及坐标变换

滚子包络环面蜗杆传动副的蜗轮是以圆柱滚子为轮齿的组合体，环面蜗杆齿面是以滚子圆柱面为母面按啮合运动关系包络展成，基于啮合关系建立标架如图1所示。图中空间固定标架σm(om-xm,ym,zm)和σn(on-xn,yn,zn)为滚子蜗轮和蜗杆的初始位置，其底矢分别为(im,jm,km)和(in,jn,kn)；滚子蜗轮与运动标架σ1(o1-x1,y1,z1)固连，并绕z1轴以角速度ω1转动，环面蜗杆与运动标架σ2(o2-x2,y2,z2)固连，并绕z2轴以角速度ω2转动；标架σ1和σ2的底矢分别为(i1,j1,k1)和(i2,j2,k2)；滚子蜗轮和环面蜗杆某瞬时的转动角位移分别为φ1和φ2，且有φ1/φ2=ω1/ω2=Z2/Z1=i12，其中Z1为环面蜗杆头数，Z2为滚子蜗轮齿数，i12为蜗杆传动副传动比；a为传动副中心距。

图1 传动副几何标架Fig. 1 Coordinate systems in the worm drive

由图1所示几何关系，有滚子蜗轮固连坐标系σ1与环面蜗杆固连坐标系σ2之间的转换关系为：

(x2,y2,z2,1)T=Mn2MmnM1m(x1,y1,z1,1)T，

(1)

1.2 滚子齿面

建立滚子蜗轮齿面在其固连坐标系的示意图如图2所示，图中r为滚子半径，u和θ为滚子齿面参数。

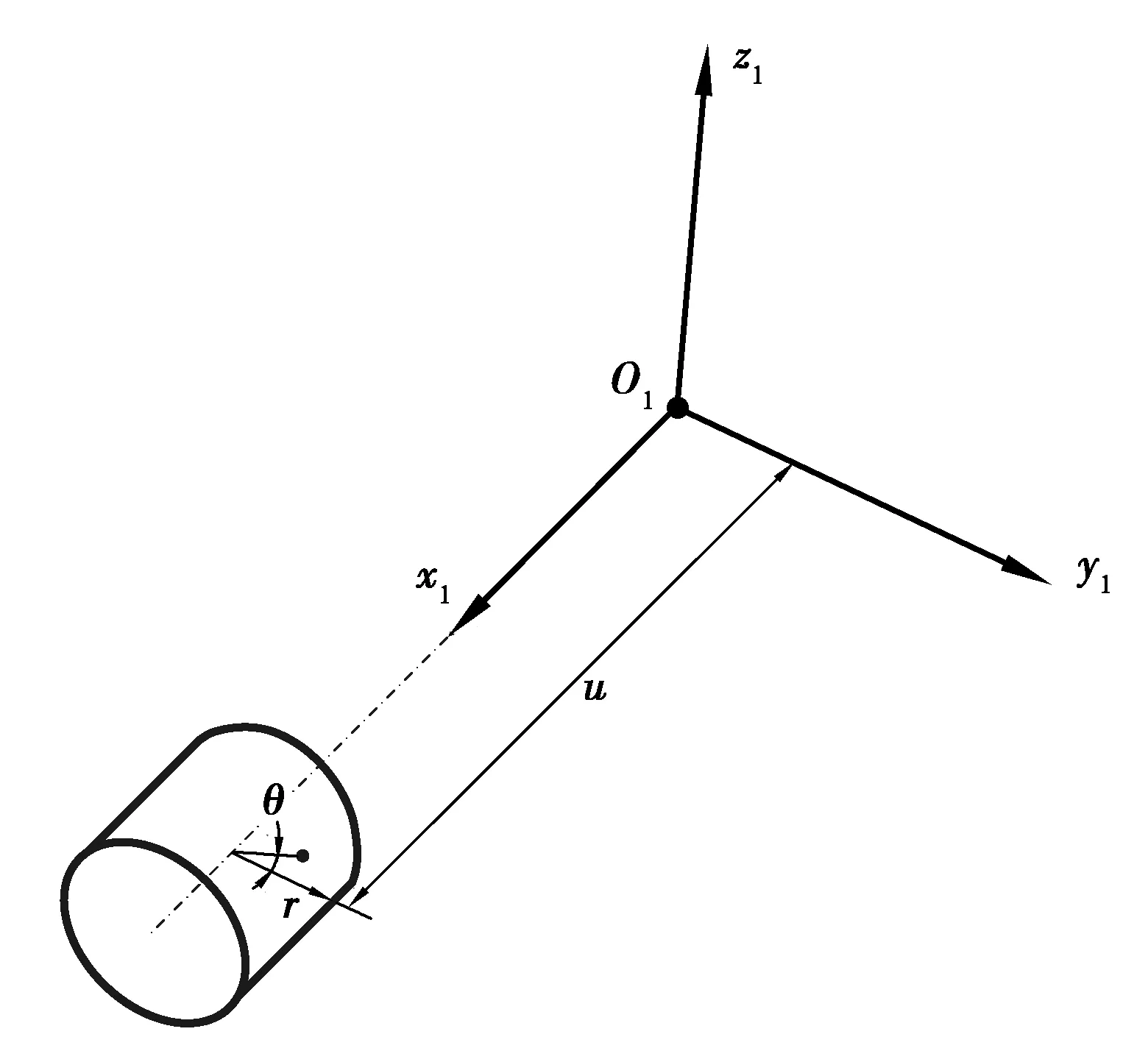
图2 滚子蜗轮齿面Fig. 2 Tooth surface of the roller worm

则滚子蜗轮固连坐标系σ1下滚子蜗轮的齿面位置向量为：

(2)

基于上述齿面方程式(2)，由微分几何关系[10]可得滚子蜗轮固连坐标系σ1下滚子齿面的单位法向量为：

(3)

1.3 传动副的啮合关系

为了表示环面蜗杆与滚子齿面的相对运动关系，同时考虑简化计算而又不失一般性，令ω2=1 rad/s, 则ω1=1/i21=i12rad/s，通过坐标变换及底矢转换，可得滚子蜗轮固连坐标系σ1下的齿面啮合点处的相对速度为：

(4)

环面蜗杆齿面与滚子齿面保持连续啮合，必须满足在传动中时刻处于相切接触状态，即满足条件[1]Φ=v(12)n1=0，得滚子蜗轮包络环面蜗杆传动的啮合函数为：

Φ(u,θ,φ1)=ai12cosθ-usinθ-ui12cosφ1cosθ。

(5)

1.4 滚子齿面接触线

滚子齿面上满足啮合方程式(5)的点即为传动副在滚子齿面的瞬时接触线。故滚子齿面接触线方程为：

(6)

1.5 环面蜗杆齿面

将滚子齿面上满足啮合方程的点转换至环面蜗杆固连坐标系，得环面蜗杆齿面方程为：

(7)

x2=acosφ2-ucosφ1cosφ2-rcosθsinφ2-rcosφ2sinφ1sinθ，

y2=asinφ2+rcosθcosφ2-ucosφ1sinφ2-rsinφ1sinφ2sinθ，

z2=usinφ1-rcosφ2sinθ。

2 含装配误差的传动副数学模型

2.1 几何标架及坐标变换

在传动副的实际装配过程中难免会产生装配误差。将传动副的装配误差分解到各个方向分量上，分别对传动副在装配过程中可能出现的中心距误差、蜗杆轴向误差、蜗轮轴向误差及轴交角误差进行分析。为了分析简便，在不失一般性的情况下假设滚子蜗轮为标准安装位置，上述所有误差均是环面蜗杆相对于滚子蜗轮而产生的，建立含装配误差坐标系如图3所示。

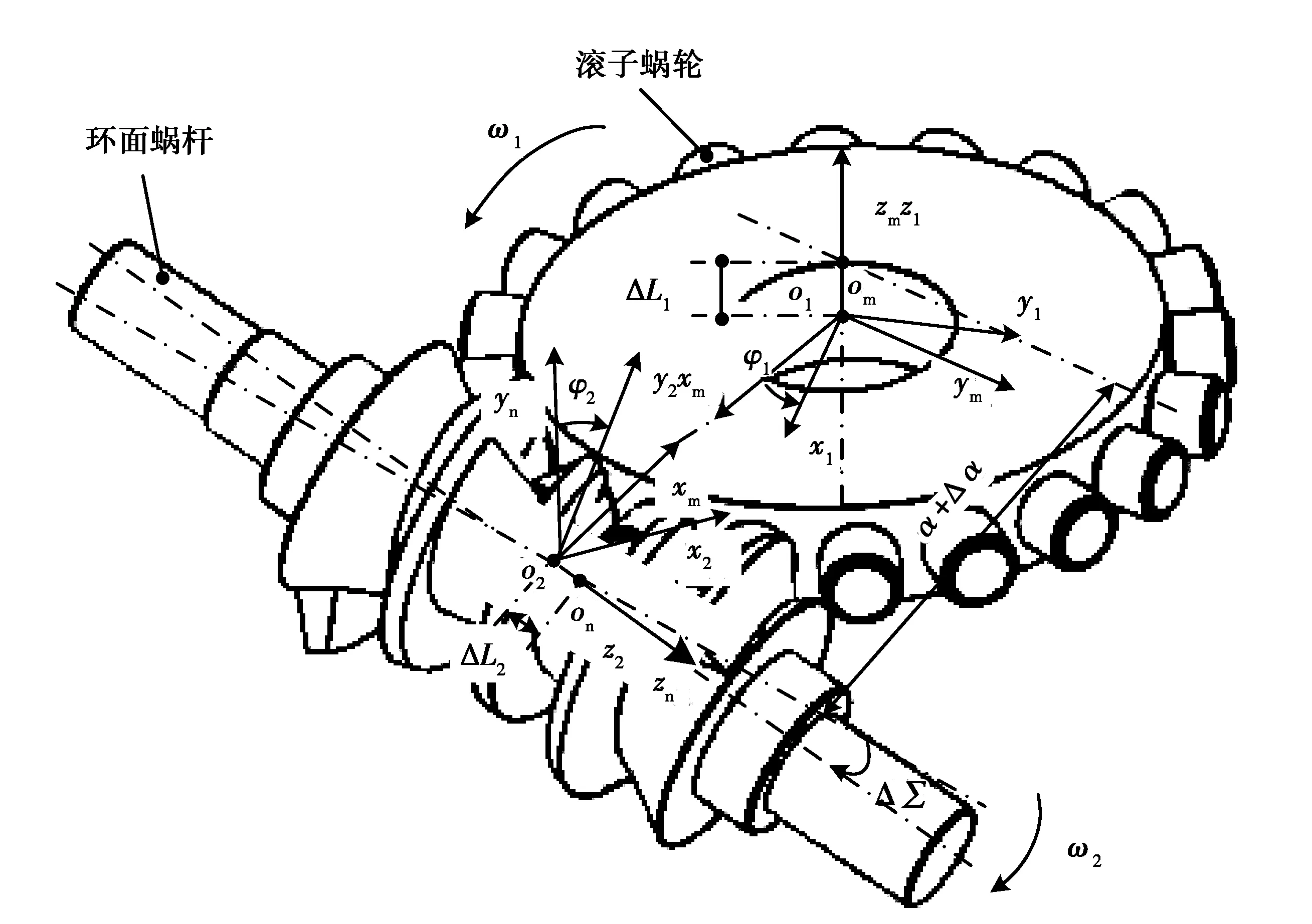
图3 含装配误差的传动副几何标架Fig. 3 Coordinate systems of the worm drive with errors

图3所示含装配误差坐标系中，考虑了蜗杆和滚子蜗轮间的误差相对位移关系，所以蜗杆固定标架σm与滚子蜗轮固定标架σn之间的变换矩阵为：

(8)

式中：Δa为中心距误差；ΔL2为蜗杆轴向误差；ΔL1为蜗轮轴向误差；ΔΣ为轴交角误差。

此外，滚子蜗轮活动坐标系σ1与其固定坐标系σm的坐标变换、蜗杆活动坐标系σ2与其固定坐标系σn的坐标变换没有发生新的误差，相对位移保持不变。

2.2 含误差的齿面方程

基于上述滚子蜗轮标准安装的假设，滚子蜗轮齿面为标准齿面，与式(2)一致。而环面蜗杆齿面则由式(8)的含装配误差变换矩阵进行转换后，得含装配误差的环面蜗杆齿面方程为：

(9)

2.3 干涉质量评价

在装配中产生蜗杆/蜗轮轴向误差、中心距误差和轴交角误差后，滚子和蜗杆会产生不同程度的干涉情况，了解各误差类型对干涉程度的影响规律对滚子包络环面蜗杆实际生产装配具有重要的指导意义。衡量它们之间的干涉质量可以用干涉体在滚子上的截面面积大小来表示。由于干涉方向的多样性，截面常会是面积较小的任意曲边形，将干涉截面近似处理为三角形或者四边形会在保留规律性的基础上很大地缩减计算量。干涉截面为图4所示的2种表现形式。

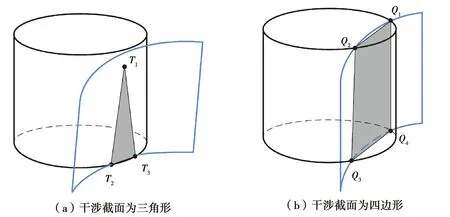
图4 两种干涉截面形式Fig. 4 Two types of the interference cross sections

图4(a)所示为三角形干涉情况，3个顶点的坐标分别为(xT1,yT1,zT1), (xT2,yT2,zT2) 和(xT3,yT3,zT3), 则总干涉面积为：

(10)

式中：

图4(b)所示为四边形干涉情况，4个顶点的坐标分别为(xQ1,yQ1,zQ1) (xQ2,yQ2,zQ2)(xQ3,yQ3,zQ3)和(xQ4,yQ4,zQ4)，则总干涉面积为：

(11)

式中：

P1=(aQ+bQ+cQ)/2，

P2=(cQ+dQ+eQ)/2。

2.4 干涉点求解

为了计算上述干涉区域面积，需获取各顶点坐标值。如图5所示滚子蜗轮齿面与环面蜗杆齿面，点j为滚子蜗轮的滚子轴线上的一点，坐标为(xj,yj,zj)，点k为环面蜗杆齿面上同一圆弧高度的环面螺旋线的一点，坐标为(xk,yk,zk)。若环面蜗杆齿面点与滚子蜗轮之间发生干涉，如图5所示情况，则：

(12)

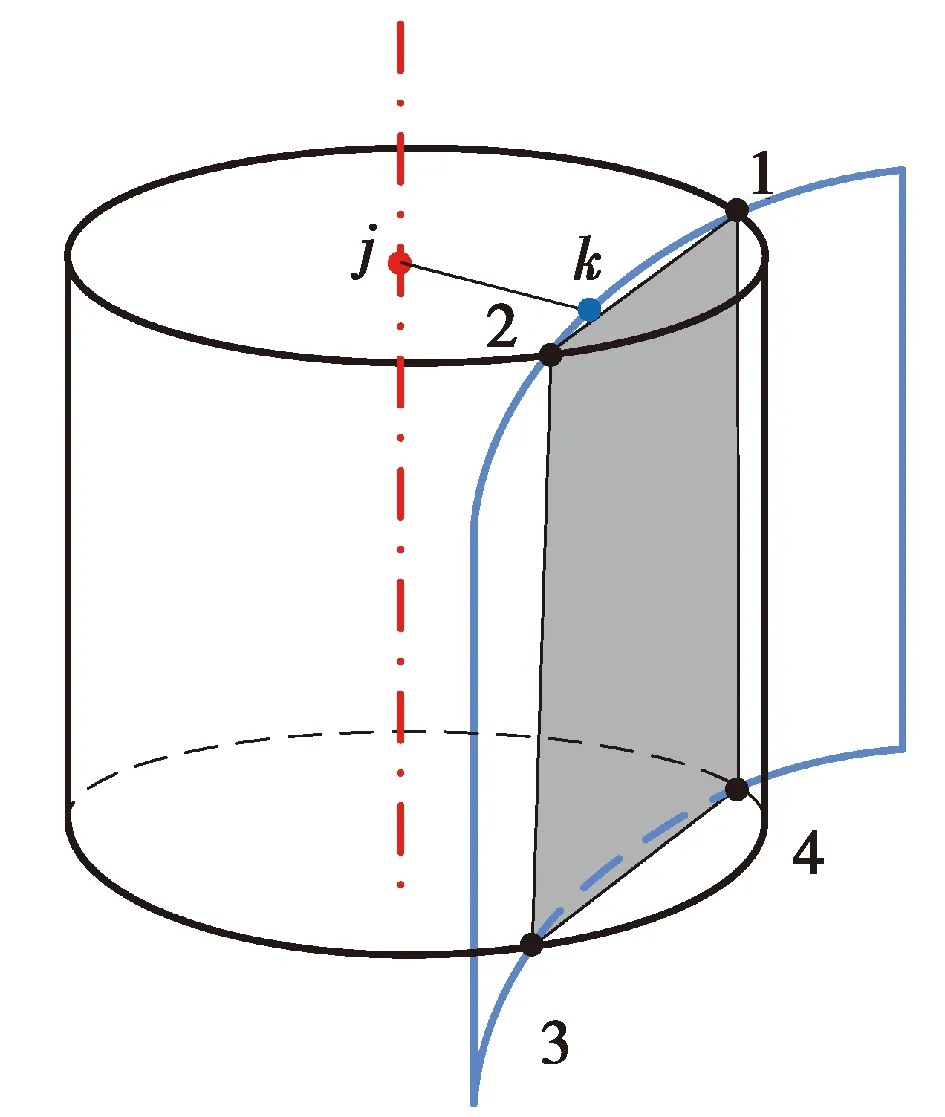
图5 齿面坐标点的距离关系Fig. 5 Distance relation of coordinate points on tooth surface

若环面蜗杆齿面点与滚子蜗轮之间不接触，则：

(13)

各顶点处应满足：

(14)

结合滚子蜗轮齿面方程式(2)、含装配误差的环面蜗杆齿面方程式(9)和顶点坐标值条件式(14)，设R为计算点在滚子蜗轮坐标系中的半径值，即j点至蜗轮旋转中心的距离，蜗杆啮合转角φ1的最小值φ11、最大值φ12及计算步长φ1h，采用图6所示求解流程编制MATLAB程序，可求解各顶点坐标值。

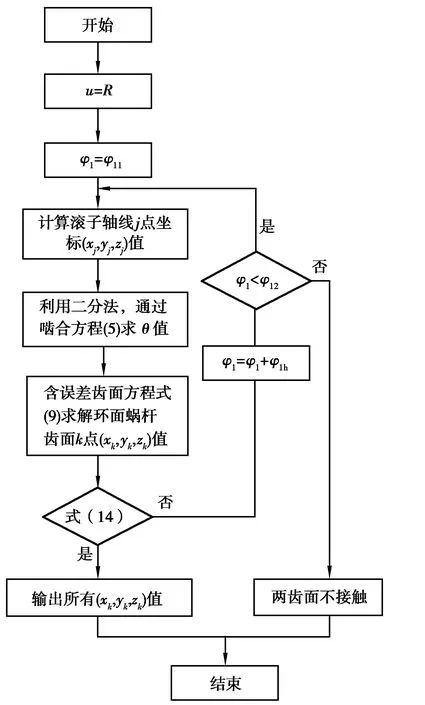
图6 干涉顶点求解流程图Fig. 6 Flow chart of solving the interference vertices

3 接触特性实例分析

含装配误差的传动副数学模型考虑了实际工况中蜗杆副误差的主要来源，这种把误差分量加入啮合模型的分析思路已见于文献[11]所研究的平面齿内齿轮一次包络鼓形蜗杆传动中。文献[11]中采用定性地观察瞬时接触线的分布来验证模型的正确性，本研究中将定量地分析干涉量随误差的变化规律。

为了验证上述理论的可行性和有效性，以表1所示参数的滚子包络环面蜗杆传动副为例，利用上述理论数学模型和含装配误差的数学模型，分析其理论接触特性和含装配误差的接触特性。

表1 蜗杆传动副基本参数

3.1 理论接触特性

根据滚子蜗轮齿面理论接触线方程式(6)和设计参数，绘制滚子齿面接触线及传动副齿面的理论接触情况如图7所示，可见滚子包络环面蜗杆传动副的理论接触线为空间螺旋曲线，分布在滚子中间平面附近。

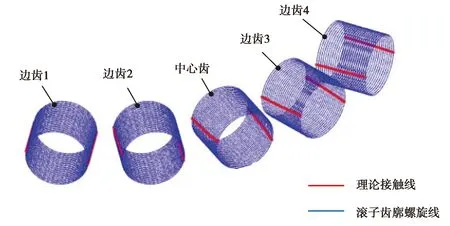
图7 滚子蜗轮齿面理论接触线示意图Fig. 7 Spiral lines generated by MATLAB

3.2 带装配误差的接触特性

实际装配中由于存在装配误差，滚子和蜗杆不再是规则的线接触，而是存在干涉情况。根据上文提出的考虑装配误差的环面蜗杆数学模型，分别考察中心距误差、蜗杆轴向误差、蜗轮轴向误差和轴交角对滚子包络环面蜗杆传动副的接触特性的影响。

3.2.1 中心距误差与干涉截面积的规律

以中心距增大为正误差、减小为负误差，进行中心距误差对滚子包络环面蜗杆传动副齿面接触的影响规律分析。由于边齿1、边齿2和边齿3、边齿4的干涉截面积总和具有对称关系，为了简化冗余而不失代表性，只分析边齿1、边齿2和中心齿左右两侧齿面的干涉截面积总和。以表1实例参数为基础，中心距误差取Δa∈[-0.10,0.10]，其余参数不变，中心距误差对滚子包络环面蜗杆传动副的干涉截面积影响规律如图8所示。

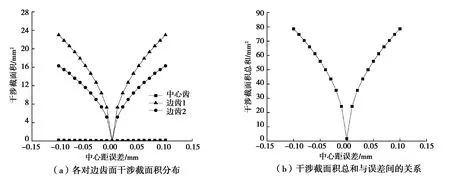
图8 中心距误差与齿面干涉面积的关系Fig. 8 Relationship between the center distance error and the interference area

从图8(a)中可以看出，各对齿对不同中心距误差的敏感程度不同。中心齿理论上干涉面积为0，但边齿的干涉截面积随中心距误差绝对值增大而增大，增大的变化率逐渐变小，外侧的边齿干涉面积大于内侧边齿。干涉截面积以零误差为轴对称分布，这是由于当误差为正时，干涉发生在滚子蜗轮右齿面；而误差为负时，干涉发生在左齿面，图8(b)中分析的是5对滚子轮齿与环面蜗杆左右侧齿面干涉截面积的累计值。

3.2.2 蜗杆轴向误差与干涉截面积的规律

由于环面蜗杆齿面的对称性，两端窜动的效果等效，故只分析其向一端窜动时的接触变化情况。考察蜗杆轴向误差ΔL2对滚子包络环面蜗杆传动副接触情况的影响，取ΔL2∈[0.00,0.10]，其余参数不变，蜗杆轴向误差对传动副干涉情况的影响规律如图9所示。

图9 蜗杆轴向误差与齿面干涉面积的关系Fig. 9 Relationship between the axial error of the worm and the interference area

从图9可以看出，蜗杆轴向窜动量对蜗杆上的各对齿的影响基本相同，总体趋势为增长率随窜动量增大逐渐减小，提示在误差产生的初期控制误差的精度尤为重要。

3.2.3 滚子蜗轮轴向误差与干涉截面积的规律

在分析滚子蜗轮的轴向误差与干涉截面积关系时，根据环面蜗杆齿面的对称性，同样只需考察其向一个方向的偏移。取ΔL1∈[0.00,0.10]，其余参数不变，计算所得干涉截面积大小如图10所示。

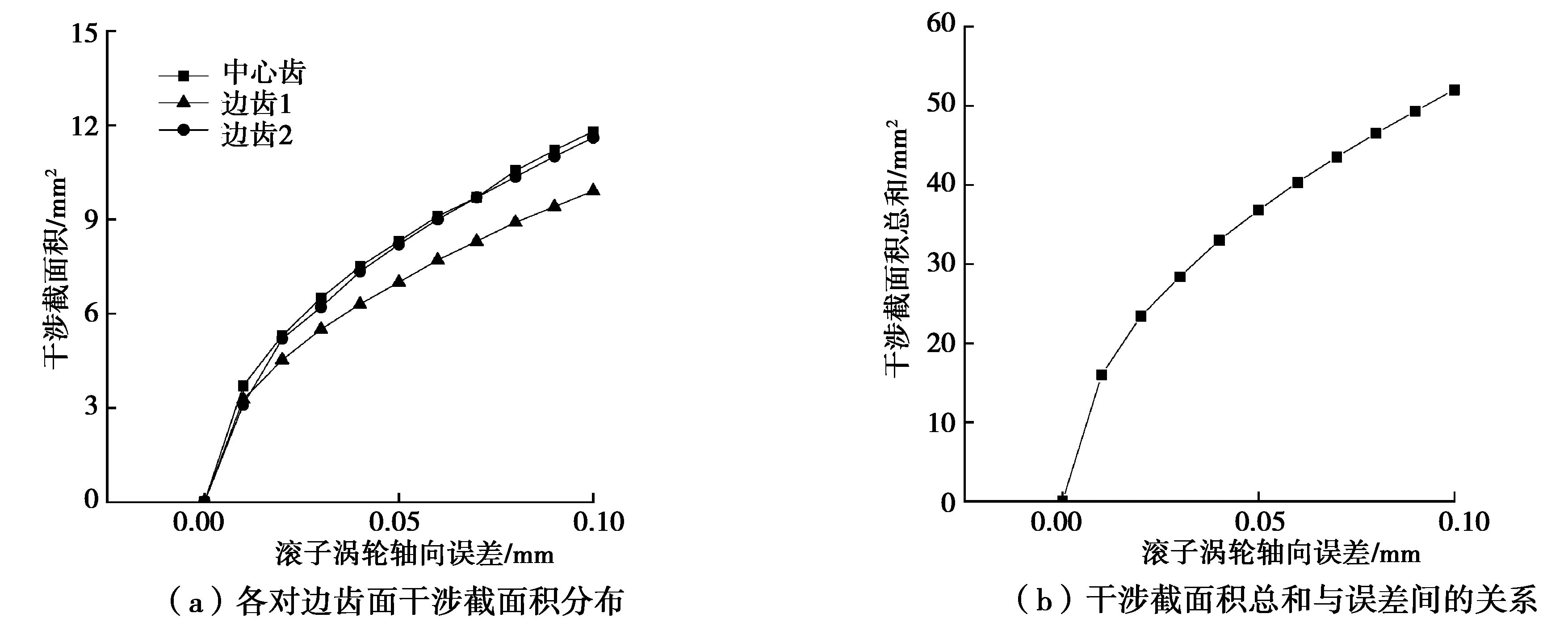
图10 蜗轮轴向误差与齿面干涉面积的关系Fig. 10 Relationship between the axial error of gear and the interference area

蜗轮轴向误差对传动副干涉的影响程度较中心距误差和蜗杆轴向误差的影响小，这是由于在沿蜗轮轴方向上啮合程度最小。滚子蜗轮轴线误差对蜗杆上的各对齿的干涉影响基本相同，呈增长变缓的增大趋势。

3.2.4 轴交角误差与干涉截面积的规律

轴交角的误差也是装配误差的重要分量之一。以沿滚子顺时针方向旋转为正，沿滚子逆时针方向旋转为负，取ΔΣ∈[-0.5°,0.5°]，其余参数不变，计算所得各对齿干涉截面积如图11所示。

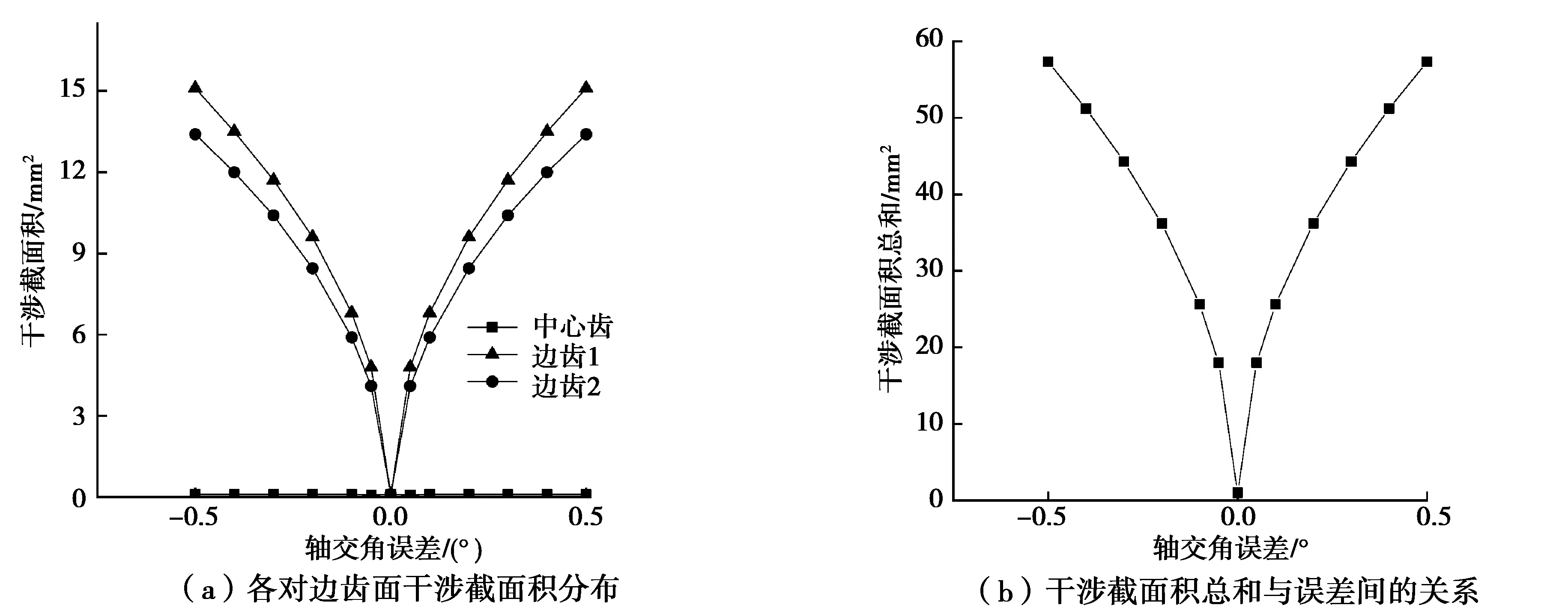
图11 轴交角误差与齿面干涉面积的关系Fig. 11 Relationship between the intersection angle error and the interference area

当轴交角误差绝对值控制在0.5°以内时，各对齿干涉量较小；且干涉截面积以误差正负值对称分布，随着误差绝对值增大而增大，然而其变化率相较之前3种误差更大。

3.2.5 各误差类型对干涉截面积的影响规律

分别对传动副在装配过程中可能出现的中心距误差、蜗杆轴向误差、蜗轮轴向误差及轴交角误差进行分析。因轴交角误差与它们量纲不同，故不在同一图内分析。由图12可以看出，在相同的数值下，蜗杆轴向窜动量误差对干涉截面积的影响最大，滚子蜗轮轴向误差对干涉截面积的影响最小。干涉截面积随装配误差增大而增大，但增长率下降。