基于F-P谐振与SPP共振的石墨烯双模吸波体设计

李从午，卞立安

(1.中电科网络空间安全研究院有限公司，北京 100166；2.中国电子科技集团有限公司 电子科学研究院，北京 100093；3.长沙理工大学 物理与电子科学学院，长沙 410114)

引 言

吸波体能够吸收电磁波，将电磁能转换为其它形式的能量，在军用和民用领域均具有良好的应用。近年来，凭借独特的光电属性，石墨烯吸波体被广泛报道[1-4]。相对于传统吸波体而言，这种新材料吸波体具有智能的电调控、超薄的结构以及超宽的吸波带等特点。在众多的吸波体中，双模吸波体在特定场景下展现出更高的实用价值，比如,可用于双波长激光发射、频率转换以及倍频效应激发[5]。因此，设计石墨烯双模吸波体在光通信系统中具有重要的意义。

独立悬浮的石墨烯吸收率很低，仅有2.3%。为了改善这种状况，常常构造各种光子晶体结构来激励法布里-珀罗(Fabry-Pérot,F-P)谐振以增强石墨烯处的电场，提高其吸收率。2013年，美国国家科学委员会将石墨烯薄层置于光子晶体缺陷腔内部，在818nm处获得了约100%的吸收率[6]。2017年，南京航空航天大学利用两端包含石墨烯介质周期结构的非对称光子晶体获得多个完美吸收模式[7]。除F-P谐振外，石墨烯光子晶体或光栅还支持表面等离子激元(surface plasmon polariton，SPP)共振，使光紧紧局域在石墨烯层。2015年，佐治亚理工学院利用石墨烯条带阵列加载的金属栅在中红外波段将石墨烯吸收率提高到94%[8]。2019年，北京邮电大学利用2维光栅与F-P谐振腔串联方式设计出双宽带太赫兹吸波体[9]。可见，激励F-P谐振或SPP共振是提高石墨烯吸收率的有效手段。

为了实现双模吸收，本文中将石墨烯条带置于光子晶体缺陷腔中，利用严格耦合波法仿真发现在F-P谐振和SPP共振的共同作用下石墨烯在太赫兹波段获得了双模完美吸收(吸收率大于90%)。在两模式下，结构阻抗与自由空间阻抗实现了良好匹配。调节石墨烯化学势能够改变吸收模式的数目；调节石墨烯条带的周期与占空比能够控制两模式的耦合程度；调节入射光方向能够同时改变模式数目和模式耦合程度。

1 石墨烯模型与仿真方法

仿真中将石墨烯建模为有厚度的3-D材料，利用介电常数εg来表征其电特性。εg可由石墨烯的表面电导率σg导出，二者的关系为εg=1+iσg/(ωε0dg)[10]，其中,ω为入射光角频率，ε0为空气的绝对介电常数，dg为单层石墨烯的厚度。电导率σg由带内部分和带外部分组成。在太赫兹波段,μc≫kBT0条件下，σg可表示为[11]:

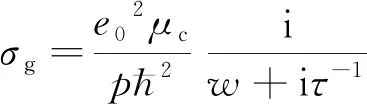
(1)

为了获得结构的吸收率，将采用严格耦合波分析(rigorous coupled-wave analysis，RCWA)法对结构进行仿真。RCWA法广泛用于求解周期结构电磁衍射问题，通过矩阵分析方法可求得电磁波的传输率T和反射率R以及吸收率A=1-T-R。具体求解步骤如下[12]：首先对光栅进行适当分层，然后对每一层内的电磁场进行傅里叶级数展开，导出光栅上层和其下层的电磁场表达式；其次，利用傅里叶级数对光栅的介电常数做展开，根据麦克斯韦方程组推导出耦合波方程；接下来，利用电磁边界条件解出每一层本征模式场的振幅、传播系数等物理参量，并确定光栅衍射效率；最后，通过分别累加前向衍射效率和后向衍射效率来获得传输率和反射率。

2 系统模型与频谱分布

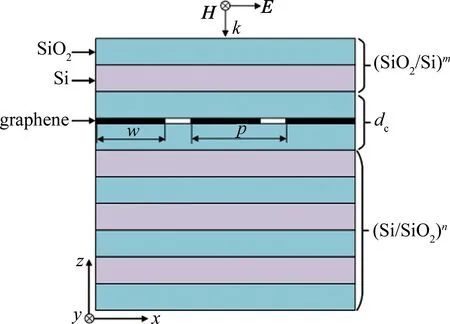
Fig.1 Defective photonic crystal with embedded graphene ribbon

结构的光响应频谱如图2所示。由于底部多层介质的光子禁带效应，系统传输率在整个目标频段内为0，以至A=1-R，提高了系统的重吸收能力。在5.1537THz和5.1970THz处，吸收率达到了0.9882和0.9825，实现了双模完美吸收，两模式依次命名为模式1和模式2。当结构阻抗等于自由空间阻抗时，结构反射率为0，系统能够获得全吸收。结构的等效阻抗能够表示为[14]:

Fig.2 Light-response spectra

(2)

式中，S11和S21分别代表端口1的反射系数和端口1到端口2的传递系数。图3中给出了阻抗Z随频率的变化情况。这里Re(Z)和Im(Z)分别代表Z的实部和虚部。显然，在模式1和模式2处，Re(Z)≈1和Im(Z)≈0成立，结构获得了良好的阻抗匹配。

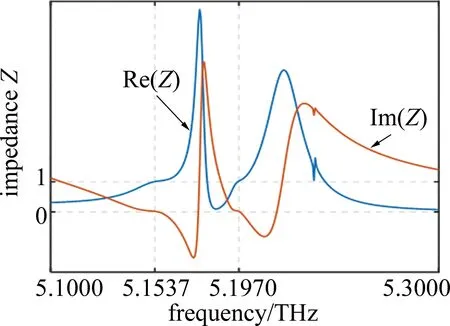
Fig.3 Variation curve of impedance Z with frequency

为了说明吸收模式的起源，图4中给出了光子晶体缺陷腔内部模式1和模式2对应的归一化磁场H分布。可见，两模式下腔内均有纵向磁场局域，其表现出F-P谐振的特点，而在石墨烯的位置，磁场表现出横向局域，其反映出SPP共振的特点。所以，两完美吸收模式是在F-P谐振和SPP共振耦合作用下产生的。

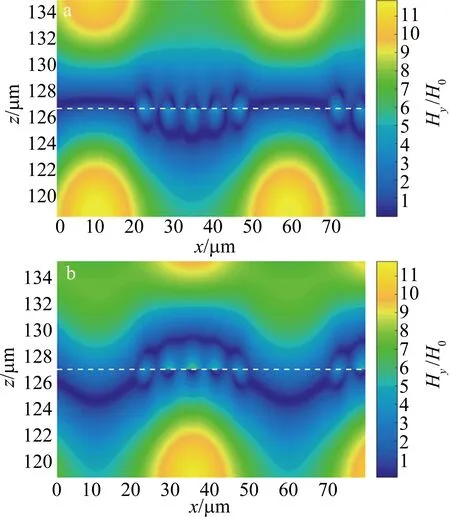
Fig.4 Normalized magnetic field distributions at mode 1 and mode 2

3 关键参量对吸收谱的影响

通过电调谐石墨烯的化学势能够显著改变石墨烯器件的性能。图5中给出了系统吸收谱随μc的变化情况。当μc较低时，系统仅有一个弱的F-P谐振吸收模，此时石墨烯表现出弱的金属性。随着μc增加，石墨烯的金属性不断增强，以至其SPP共振效应开始凸显。此外，F-P谐振模式向高频方向移动，这种现象可用微扰理论来解释。腔内谐振波长偏移满足以下关系[15]:

Δλ/λ=Δε·ΔV/V

(3)

式中,λ为谐振波长，Δλ为波长的偏移量，Δε为腔的扰动引起的介电常数的变化，ΔV为扰动体积，V为腔的体积。μc增加导致Δε减小，所以F-P谐振模式蓝移。当μc>0.5eV时，系统在F-P谐振和SPP共振的双重作用下获得了两个完美吸收模式;当μc=0.7eV，两模式完全耦合，二者峰峰距很小，其可用于探测毗邻的入射光。

Fig.5 Varying absorption spectra with the chemical potential of graphene

石墨烯作为结构中唯一的吸波材料其尺寸直接影响着系统的光吸收性能。图6中分别给出了石墨烯条带周期p和占空比η的变化对系统吸收率的影响。在图6a中，随着p的增加，SPP共振模幅度和位置均随之改变，以至完美吸收模式数目不断变化。当p为0.7λ0或0.8λ0时，系统保持双模吸收，且两模式处于耦合状态。在图6b中，随着η的增加，F-P谐振模式蓝移，而SPP共振模位置保持稳定。当η=0.7时，两模式完全耦合。可见，调节石墨烯条带周期和占空比可以直接控制模式间的耦合程度，改变模式峰峰距，这有利于对不同频差的双路光信号进行探测。对比完整石墨烯薄层加载的缺陷光子晶体吸波体[6]，石墨烯条带加载方式能够提高系统调控的2个自由度。

图7中给出了入射光的角度对系统吸收谱的影响。当入射光少许偏离垂直入射，模式数目增加。由于F-P谐振模式不会分裂，所以模式数目增加来源于SPP共振模式分离[16]。垂直入射时，±m级次SPP共振模式简并；斜入射时，简并性被破坏，模式开始分离，分别向高频和低频方向移动。随着入射角度增大，SPP共振模式衰减愈发严重。当θ=4°时，系统将仅仅保留高吸收的F-P谐振模式。

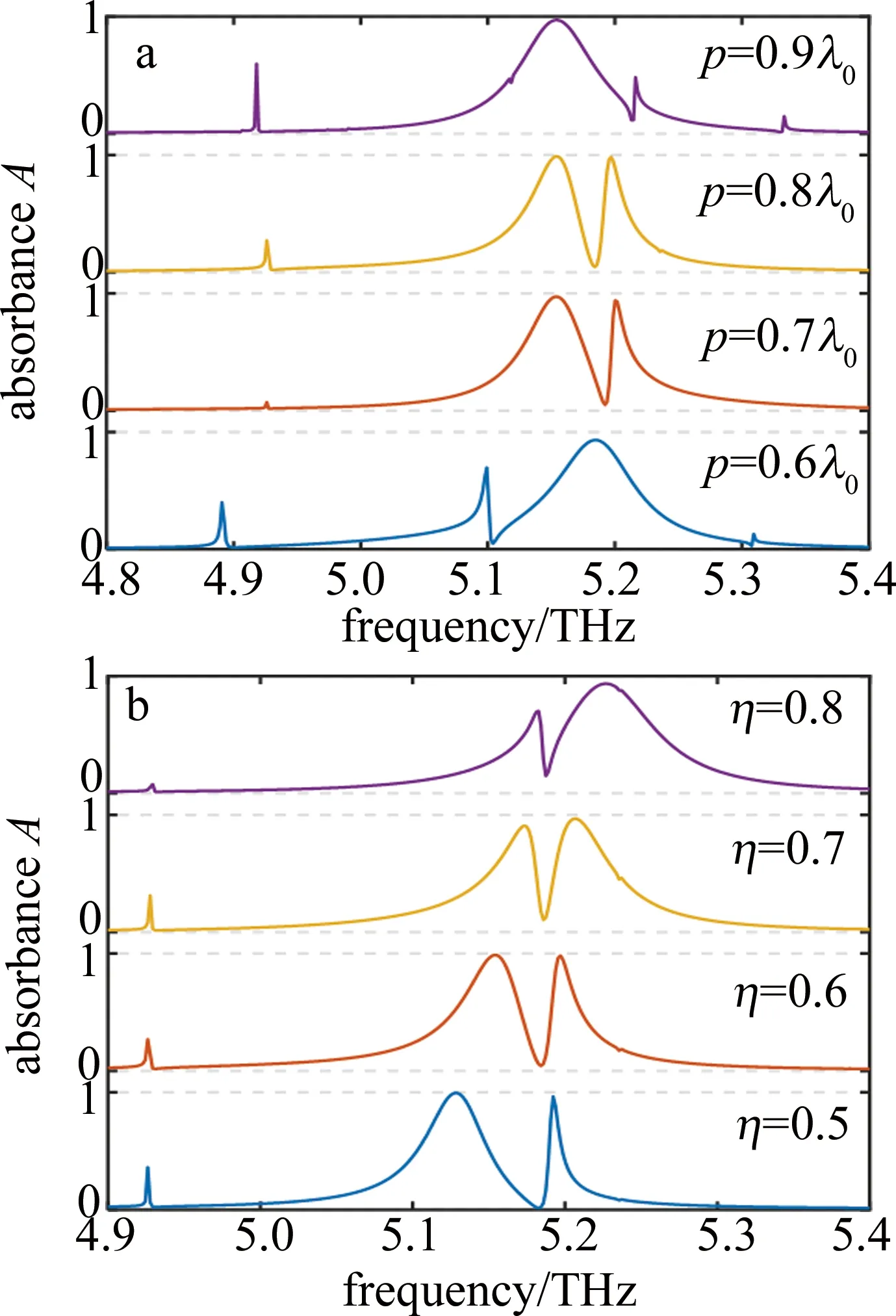
Fig.6 Varying absorption spectra with the geometries of graphene ribbon

Fig.7 Effect of the angle of incident light on system absorption spectra

4 结 论

利用嵌有石墨烯条带的光子晶体缺陷腔实现了石墨烯的双模完美吸收。通过严格耦合波法仿真发现，两个模式分别出现在5.1537THz和5.1970THz处。此时，结构等效阻抗等于自由空间阻抗。观察归一化磁场分布图，判定二者起源于F-P谐振和SPP共振的共同作用。在器件制备过程中，通过控制石墨烯条带刻蚀尺寸能够制约两模式的耦合程度；器件制备完成后，两模式的耦合能够通过调节石墨烯外加电压以及入射光角度来控制。耦合的吸收峰能够探测毗邻的光信号，其在非线性光学系统中可能有重要的作用，如检测3阶交调后的光信号。