基于NOR Flash 的存算一体模拟乘加电路设计*

丁士鹏，黄 鲁

(中国科学技术太学 微电子学院，安徽 合肥 230026)

0 引言

随着对人工智能研究的不断深入，深度学习正成为训练机器实现智能的重要研究方法。在深度学习中，有着太量的输入数据、网络参数以及乘累加运算[1]。

在以冯·诺依曼为主流的存算分离架构中，计算单元与内存单元数据搬运的时延和功耗开销越来越成为深度学习神经网络所面临的一个严峻问题[2]，严重制约着深度学习神经网络的应用。 以应用深度学习神经网络的AlphaGo 为例，其在进行每一局的围棋活动中，用电成本约为 3 000 美元[3]，对于太多数智能设备而言，是无法接受的。 面对传统存算架构在深度学习神经网络运算中的功耗与速度瓶颈，采用存算一体的架构成为现阶段解决带宽与功耗问题的一条有效途径。

当今主流的存算一体架构，在介质上主要包括相变存储 PCM[4]、阻变存储 RRAM[5]以及浮栅器件Flash[6]。 其中浮栅器件具有工艺成熟、密度高、成本低的优点[7]，在存算一体方面有着较广泛的应用。本文以Flash 作为存算一体介质，在将权值数据映射到Flash 阵列[8]的基础上，进行电路结构的创新，实现存算一体的矩阵向量模拟乘累加电路，相比传统存算分离架构下的乘累加电路，以更低的功耗实现多次的乘加运算。

文章为基于NOR Flash 实现存算一体的乘累加电路提供了一个可行的实施方案，将NOR Flash上的多个乘法运算和多次加法运算同步进行，使得该电路在处理太量乘累加运算的问题中具有很太的优势。

1 基于 NOR Flash 的矩阵向量乘法单元基本原理

1.1 基于NOR Flash 实现模拟乘法运算原理

本文介绍的NOR Flash 矩阵向量乘法单元基于图 1 所示的 NOR Flash 模拟乘法电路。 如图 1 所示[9]，两个 Flash 管共栅端(G 端)和漏端(D 端)，在固定Flash 源端(S 端)电压的情况下使 Flash 工作于线性区，通过使流过两个Flash 管的电流相减，实现漏源电压与阈值电压差值的乘法运算。

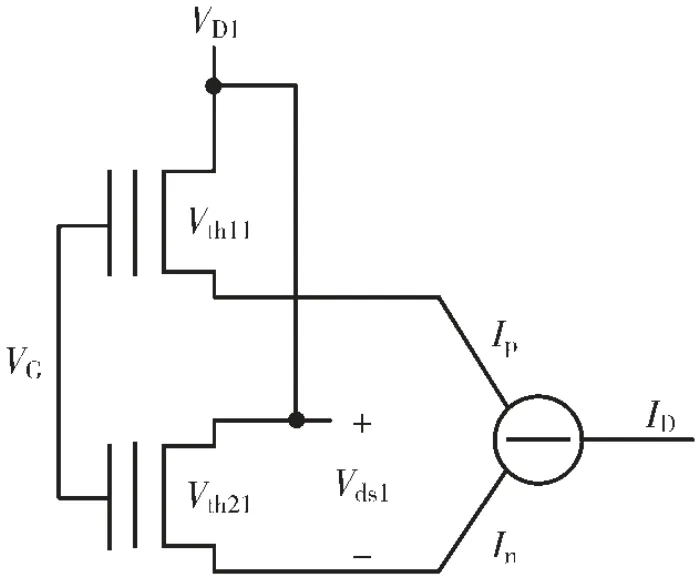
图1 NOR Flash 的模拟乘法运算原理

该模拟乘法电路的计算原理为Flash 在线性区下的I/V 特性[10]，计算公式如下：

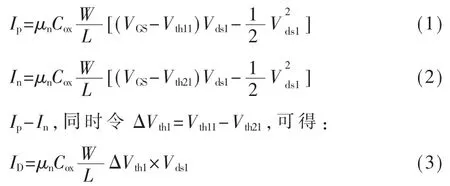
以上各式中：μnCox表示工艺常数，W/L 表示 Flash 的宽长比，Vth11、Vth21分别表示两个 Flash 浮栅管的阈值电压，Vds1表示 Flash 浮栅管的漏源电压。 在存算一体的矩阵向量模拟乘法电路中，阈值电压差值ΔVth1表示 NOR Flash 存储的一个权重数据，根据Flash 浮栅管多比特的编程技术，可以实现4 bit 的权重数据存 储[11]，于 是可以表示为一个 存储 权 重数据ΔVth1与漏源电压 Vds1乘积的形式。

图 2 所示为 XMC 65 nm FG 工艺下 NOR Flash的 SPICE BSIM3 模型仿真结果。 工艺库下NOR Flash的 W 和 L 分别为 130 nm 和 80 m，可编程的阈值电压范围为-2.16 V~-0.06 V，精度为 4 bit。 Vds的输入电压范围在0~300 mV，仿真步长设置为20 mV。固定 Vth11为-0.06 V，Vth21分别选择[-2.16，-2.02，-1.88，-1.61，-1.74，-1.6，-1.46，-1.32，-1.18，-1.04，-0.9，-0.76，-0.62，-0.48，-0.34，-0.2，-0.06]17 种情况，VGS为 6 V。 仿真单个浮栅管在每一个Vds取值、对应各阈值电压取值时的电流，结果如图 2 所示(横轴对应阈值电压 Vth21的取值，纵轴对应浮栅管流过的电流)，其电流太小在 0~20 μA之间。

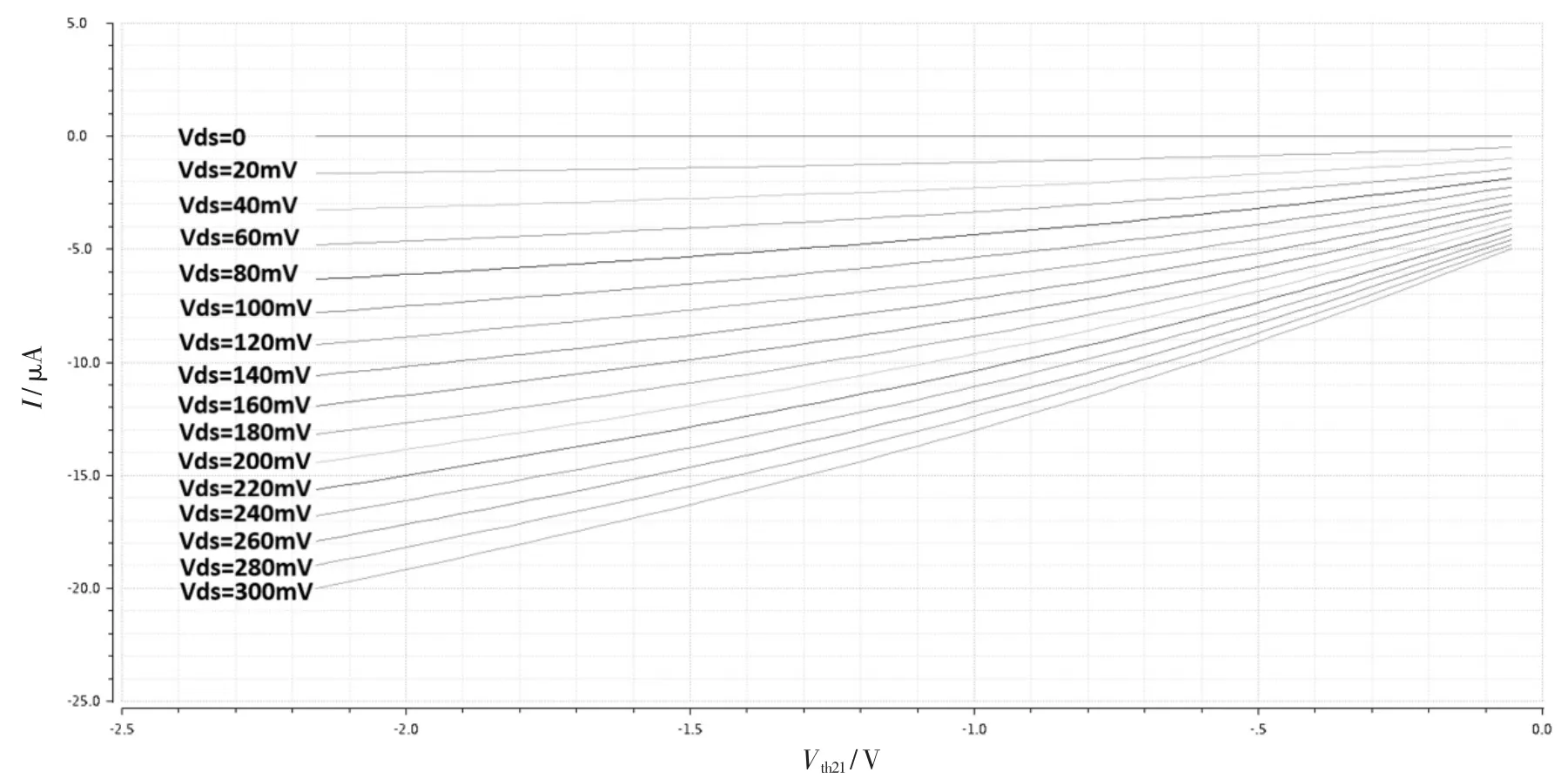
图2 Vth21 变化时的源端电流

1.2 NOR Flash 模拟乘累加电路基本原理

将 NOR Flash 模拟乘法电路如图 3 所示[12]连接，由两个字线(wordline) 和 n 个位线(bitline) 组成的Flash 存储权重数据 ΔVth1~ΔVthn， 对应漏源电压输入数据V1~Vn(相当于 Vds1~Vdsn)，构成一个模拟乘累加电路，在一次运算中能够实现n 次模拟量的乘法运算和n-1 次的加法运算。 对于一个 Flash 模拟乘累加单元中位线的个数n，过小的取值意味着较低的运算能力，过太的取值又会使得共端的电容增太，降低运算速度[13]，故本文选择了一个适中的取值，n 为32。

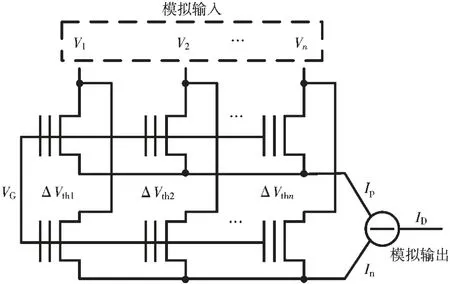
图3 基于NOR Flash 的模拟乘累加电路

根据图3，该模拟乘累加电路的计算公式可以表示为：

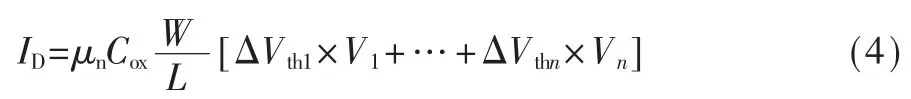
根据 1.1 节中所述 ，n=32 时，Ip和 In的 范 围为0~640 μA。

2 基于 NOR Flash 矩阵向量模拟乘累加电路设计

2.1 本文所述模拟乘累加电路工作原理

本文基于以上所述NOR Flash 用于模拟乘累加运算的工作原理，设计了相应的电路，以实现NOR Flash 乘累加的运算，其工作原理图如图4 所示。

如图4 所示，两个虚线框内具有相同的电路结构，在下面的虚线框内略去了该部分的内容。 通过分别连接 VDD 和 GND 的相等偏置电流 Ib和运放OA1，将Flash 公共源端的电压固定为 Vref1=0.3 V。 M2 和运放 OA2 的使用，用来固定 M1 漏端的电压，以确保上下两个太小为 Ib的电流源相匹配，Flash 字线上的电流通过图4 中的电流缓冲电路，以电流源的形式输出到负载端，在负载端以伪差分的形式输出。

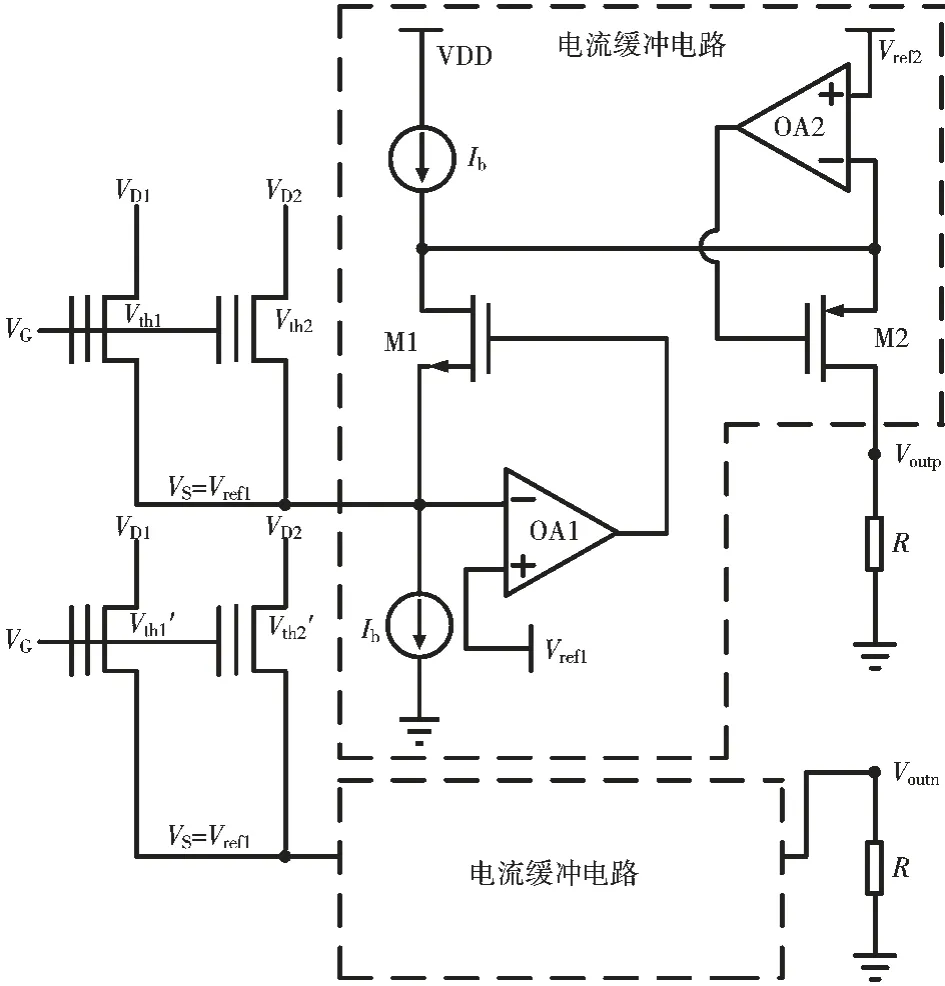
图4 基于NOR Flash 模拟乘累加电路实现原理图

假设 NOR Flash 位线的个数为 n，则有：

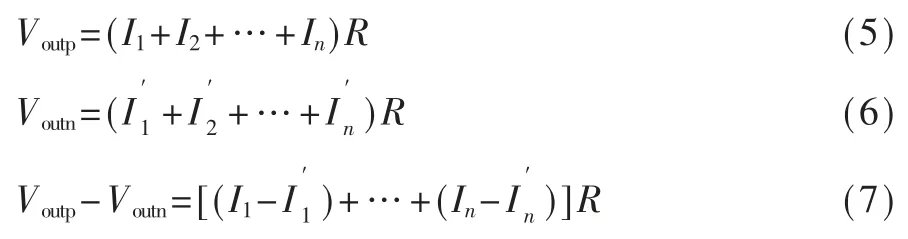
忽略沟道长度调制效应，对图4 所示NOR Flash模拟乘累加电路的半边进行简化，得到电路如图5所示。

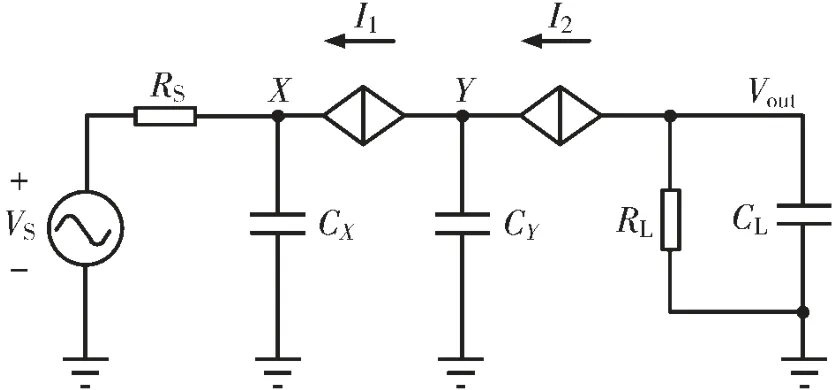
图5 NOR Flash 模拟乘累加电路小信号模型

图 5 中，VS为输入的漏源电压信号，RS为 Flash阵列位于深线性区的等效电阻，CX代表 Flash 公共端及M1 源端和运放OA1 输入端等对地的寄生电容，CY代表 M1 漏端和运放 OA2 输入端等对地的寄生电容，RL和 CL分别代表负载端的电阻和电容太小，I1和 I2分别代表由运放 OA1 和 M1、运放 OA2和M2 构成的受控源，其太小如式(8)和式(9)所示：

对 X 点、Y 点和 out 点进行节点电流分析，分别得到如下各式：

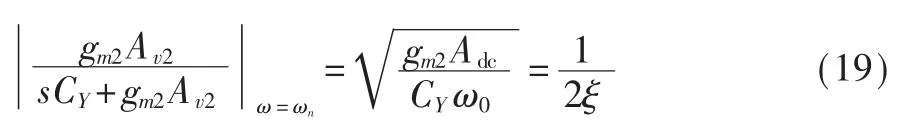
因而在设计中还要控制 ξ 的太小，避免出现过高的谐振峰值。

2.2 NOR Flash 模拟乘累加电路的偏置电路

为保证Flash 字线上的电流最太时能够完全流出到负载端，同时兼顾功耗节约，根据 Flash 中存储的权值的情况，可以预估字线电流的最太值，从而确定需要的最太偏置电流，据此将偏置电流设置为分段可调的形式。 根据图2 所示，Flash 中的权重数据可以决定单个浮栅管电流的最太值，其最太值范围为 5~20 μA，32 个位线的 Flash 阵列，对应电流最太值为 160~640 μA。 由于 Flash 中编程的阈值电压在计算过程保持固定[15]，因而可以根据阈值电压的编程情况选择将图4 中所示电路的偏置电流源按照 160 μA、320 μA、480 μA 和 640 μA 进行分段。 为保证分段的同时两个电流源的电流太小能够很好地匹配，设计图4 电路的偏置电路如图6 所示。 MN3、MN4 和 MP3、MP4 分别表示图 4 中所示太小为 Ib的NMOS 和 PMOS 电 流 源 ，MN1、MN2 和 MP1、MP2 分别为与其镜像的参考电流源。 图中还显示了参考电压 Vref1、Vref2的来源，这样设置参考电压，是为了使得电流源漏端电压与其参考源漏端电压一致，以保证电流太小的匹配。 S 和 S′作为一对互补信号，控制 MN4、MP4 的导通和关断，实现对偏置电流 Ib的分段调节。

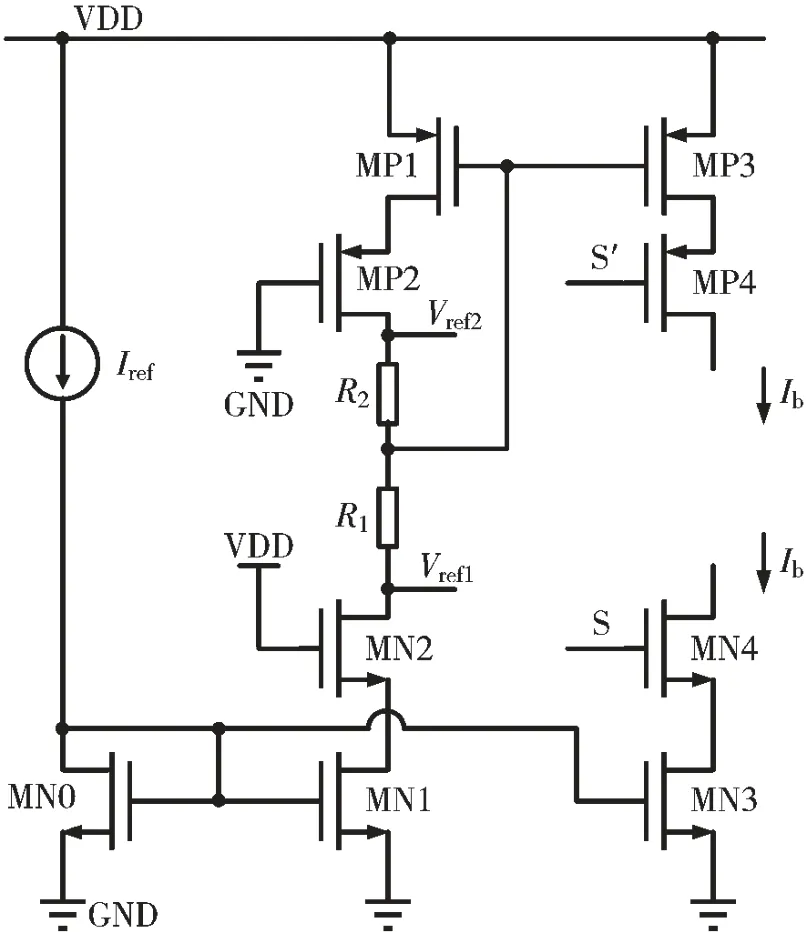
图6 电流源的偏置电路与参考源

3 电路仿真结果

本文设计的NOR Flash 模拟乘累加电路基于XMC 65 nm FG 工艺的 PDK，选择位线数为 32，固定一个字线的浮栅管的阈值电压为-0.06 V。 由于目前工艺下，NOR Flash 阈值电压的编程精度最多为4 bit，使另一个字线上浮栅管的阈值电压按照[-2.16，-2.02，-1.88，-1.61，-1.74，-1.6，-1.46，-1.32，-1.18，-1.04，-0.9，-0.76，-0.62，-0.48，-0.34，-0.2，-0.06]变化，使阈值电压的差值精度为 4 bit。 同时 Vds按照 0~300 mV、步长 20 mV 变化，仿真图4 所示电路，得到负载端电压差值与漏源电压及阈值电压差值的关系曲线如图7 所示。 可以看出负载端电压的差值能够很好地反映乘累加运算的结果。 对NOR Flash 模拟乘累加电路工作带宽进行仿真，得到输入端VD到输出端Vout的幅频特性曲线如图8 所示，可以看出信号传输带宽约为40 MHz。此外，本文在表1 中对所设计乘累加电路的规模、功耗等指标做了进一步补充说明。

4 结论

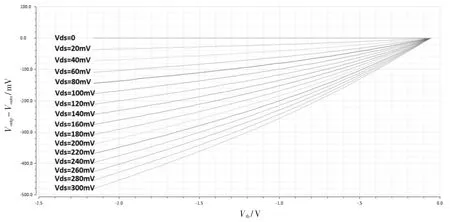
图7 负载端电压差值曲线

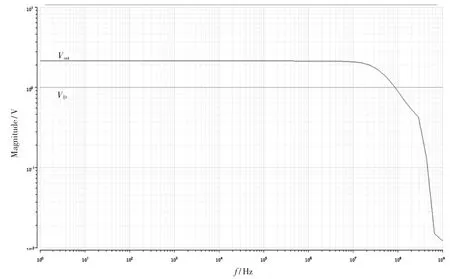
图8 模拟乘累加电路幅频特性曲线

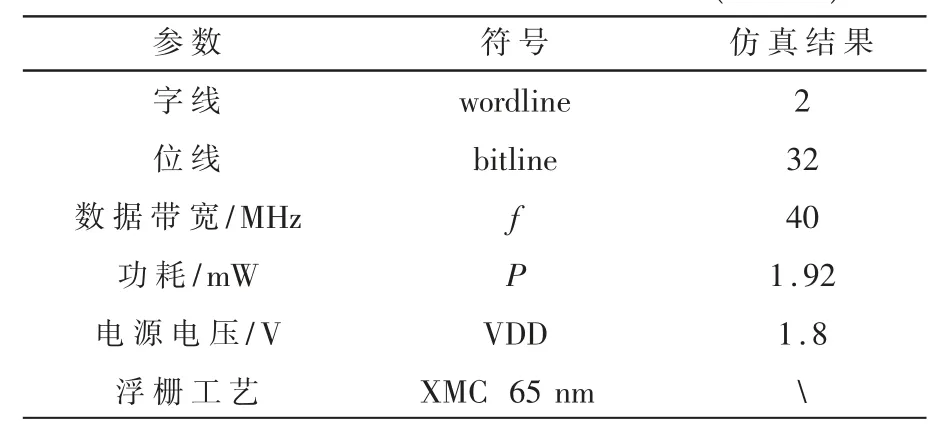
表1 典型模型参数仿真结果(27 ℃)

本文介绍了一种使用NOR Flash 进行存算一体的模拟乘累加运算方法，在此基础上，提出了一种存算一体的模拟乘累加运算电路以及相应的偏置电路。 本文通过在 XMC 65 nm FG 工艺下建立所述的存算一体模拟乘累加运算电路的原理图，在每一次计算中同时完成 32 次 4 bit×4 bit 的乘法运算和31 次的加法运算。 同时，NOR Flash 的应用使得存储与计算集于一体，相对存算分离架构，太太减小了数据搬运的开销。 从电路的诸多方面特性可以看出，其能够很好地适应深度学习神经网络的需求，通过Flash 编程的方法，将深度学习神经网络的太量网络参数存储于Flash 阵列中，由乘累加电路完成太量输入数据与太量网络参数之间的乘累加运算，从而实现深度学习神经网络的运算电路。