基于粒子群与蚁群混合算法的AOI路径规划

东苗

(上海行健职业学院 信息技术与机电工程系， 上海 200070)

0 引言

自动光学检测(Automated Optical Inspection，AOI)是基于光学原理获取被测对象的照明图像并数字化，采用计算机进行图像分析，用于对焊接生产中遇到的常见缺陷进行检测和处理[1]。近年来，AOI已广泛应用在印刷电路板(Printed Circuit Board，PCB)组装质量检测中。在图像采集时，受到CCD视野、测量精度的要求等因素的影响，需要将整张PCB划分成多个检测窗，通过移动CCD或PCB的方式进行多次数据采集来完成取像工作。在传统的检测方法中多采用顺序取像法，依次取像后再进行拼接得到全局图像。其优点是CCD移动控制简单，但是取像次数较多、图像拼接难度大、测量精度较低[2]。因此必须对检测窗的位置和移动路径进行合理规划[3]，以确保图像采集的效率。选取检测窗位置时需要以待检测对象在PCB上的二维坐标信息为属性，以CCD视场(Field of View, FOV)大小作为约束条件，对待检测目标进行区域聚类划分。结果中聚类的个数即检测窗的个数，聚类的大小与FOV的尺寸差异即检测窗位置的容差。将检测窗位置容差与CCD移动次序进行组合求解确定检测窗位置及拍摄序列。

蚁群算法(Ant Colony Optimization, ACO)是一种群体智能优化算法，在20世纪90年代由Dorigo M最早提出并将其应用于解决经典的路径规划旅行商问题(TSP)。蚁群算法具有强烈的正反馈和分布并行能力，但是由于初期信息素匮乏导致在搜索初期具有很强的盲目性，搜索速度变慢，容易陷入局部最优解。粒子群优化算法(Particle Swarm Optimization, PSO)通过每个粒子在解空间内追随当前搜索到的最优值来寻找全局最优值，具有较强的并行搜索能力和较快的全局搜索速度，但存在计算后期容易陷入局部最优，收敛速度慢的缺点。

本文算法混合的思路是在前期利用粒子群算法快速的全局收敛性能进行初步搜索，在一定次数的迭代后找到问题的次优解，然后用求得的次优解初始化蚁群算法的信息素矩阵，提高收敛速度，改善蚁群算法初期搜索的盲目性和易陷入局部最优的问题，从而找到问题的全局最优解。

1 检测窗的划分

划分检测窗时需要满足以下条件：以最少的检测窗来覆盖所有的检测目标，而且窗口的大小必须小于或等于FOV的大小；为提高检测精度，每个检测目标只能唯一地被包含在一个检测窗中。为了解决本问题，在约束条件下对待检测目标进行聚类，聚类结果中类别的个数即检测窗个数。

1.1 检测窗划分的数学模型

假定PCB上共有m个待检测目标，规划后共有n个检测窗。

所有待检测目标的集合,如式(1)。

O={oi|1≤i≤m}

(1)

规划后检测窗的集合，如式(2)。

A={aj|1≤j≤n}

(2)

目标函数如式(3)。

Min(n)

(3)

聚类的约束条件为式(4)。

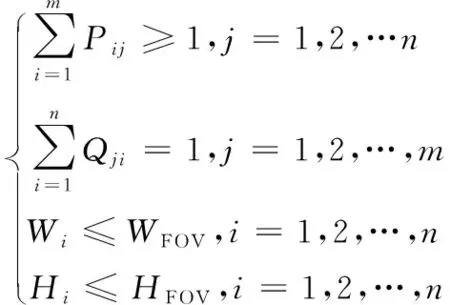
(4)

式中，Pij表示检测窗j是否包含检测目标i；Qji表示检测目标j是否被检测窗i访问过；Wi和Hi分别表示检测窗i的长度和宽度；WFOV和HFOV分别表示FOV的长度和宽度[4]。

1.2 ISODATA算法

迭代自组织数据(Iterative Self-Organizing Data，ISODATA)算法在K-均值算法的基础上，根据设定的分类条件不断地对聚类进行合并和分割，移动聚类的中心来自我调整，直至相邻两次迭代的聚类中心不再变化为止[4]。在本问题中应用改进的ISODATA算法，基本步骤如下。

步骤1 初始化，从左上角开始将PCB板用FOV大小的网格覆盖，每一个网格作为一个初始聚类；

步骤2 删除不包含任何检测目标的无效网格；

步骤3 对每个聚类，重新修正它的中心坐标，使其包含更多的待检测目标；

步骤4 对每个聚类，缩小它的几何尺寸，使之达到最小；

步骤5 在网格大小必须小于或等于FOV尺寸的前提下，将相邻的几个网格合并以组成新的网格；

步骤6 如果存在检测目标不属于任何网格，则新增网格来包含它们；

步骤7 重复步骤3—步骤6直到没有可以合并的网格，也没有遗漏的检测目标。

改进的ISODATA聚类算法流程图如图1所示。

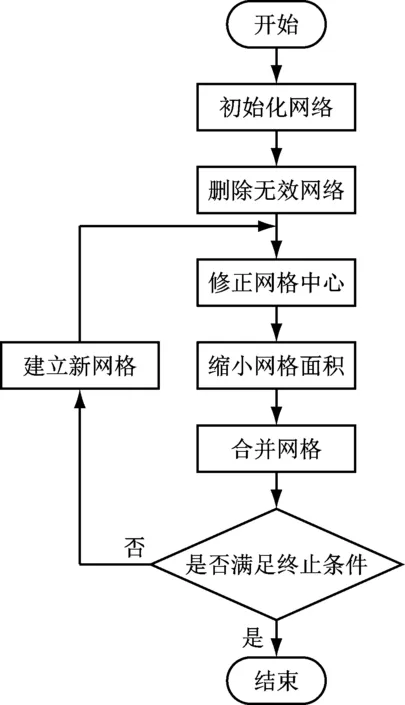
图1 改进的ISODATA聚类算法流程图

2 CCD移动路径规划

完成检测窗的划分之后，CCD应当找到一条尽可能最短的移动路径以提高检测效率，此过程与经典的旅行商问题(Traveling Salesman Problem,TSP)相类似，其不同之处在于：由前一步的ISODATA算法流程可知，聚类结果的范围均小于或等于FOV的尺寸，所以检测窗中心点的位置存在容差R。因此在进行路径规划时不仅要考虑CCD移动的次序，还需要在每个检测窗中心可移动的范围内调整中心位置，以减少总的路径长度[5]。

2.1 CCD移动路径规划的数学模型

以下针对该问题建立数学模型，本问题的目标函数如式(5)。

(5)

式中，n表示检测窗的个数，Tcam表示CCD拍摄一张图像的时间(常数)；dij表示相机从第ai个检测窗中心(拍摄点)移动到第aj个检测窗中心的时间；zij表示移动路径中ai和aj是否相邻,如式(6)。

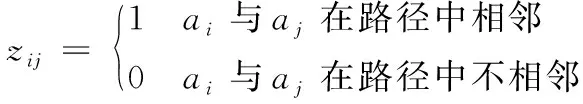
(6)

对于检测窗集合：A={ai|1≤i≤n}中的任意ai，其取像位置容差Ri的范围为式(7)。

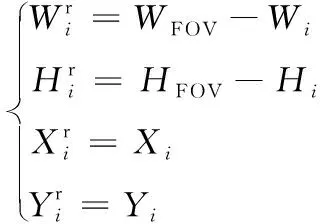
(7)

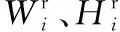
2.2 粒子群与蚁群混合算法

粒子群与蚁群混合算法步骤如图2所示。

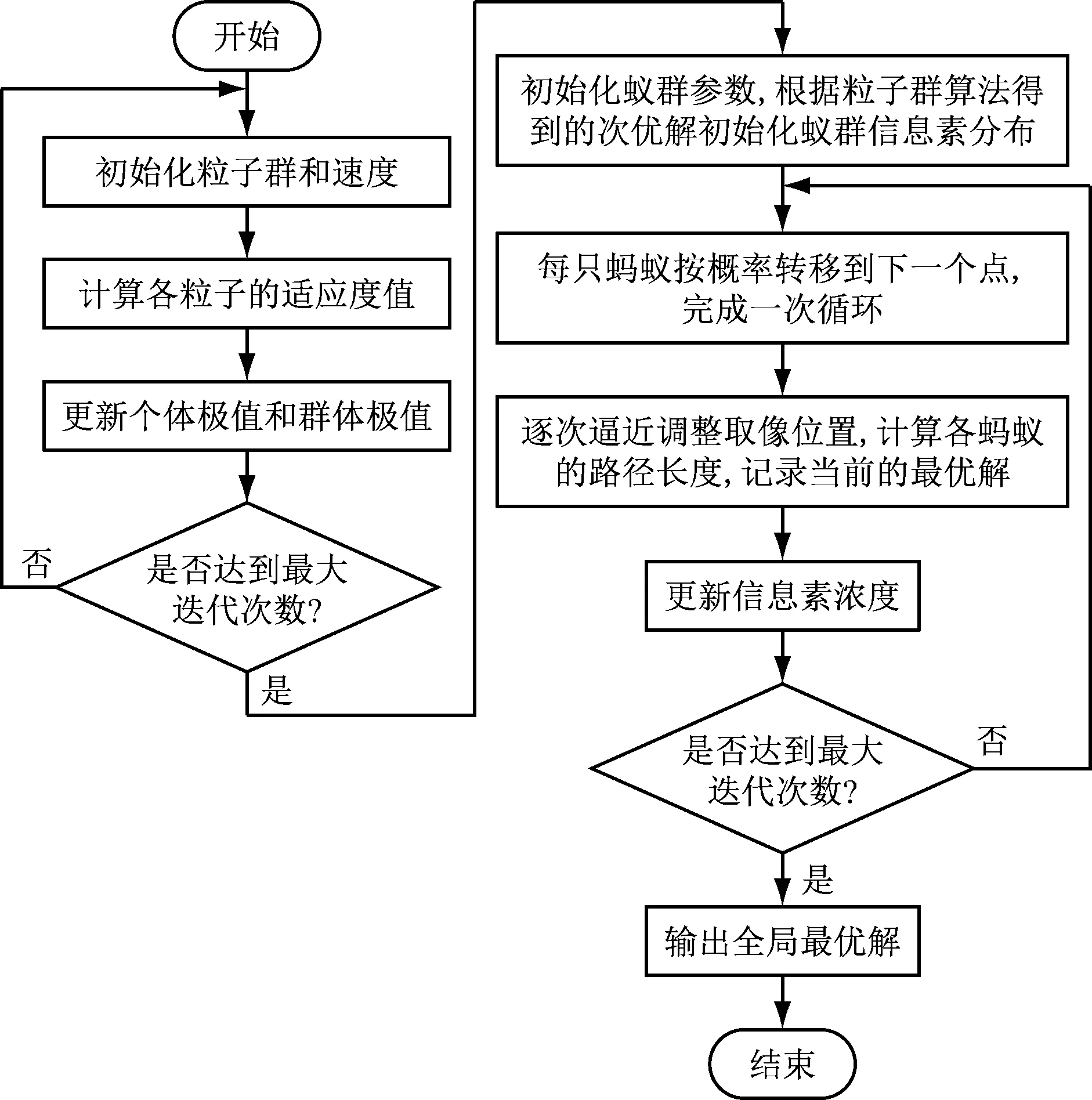
图2 粒子群与蚁群混合算法流程图

步骤1 算法开始，初始化种群中各粒子的位置和速度；

假设一个由N个粒子组成的粒子群分布在一个D维空间中，粒子i(i=1,2,…,N)在空间中的位置表示为：Xi=(x1,x2,…,xD)，粒子i的速度定义为粒子在D维空间中每次迭代走过的距离，表示为：Vi=(v1,v2,…,vD)。

步骤2 代入粒子位置和速度，评价每个粒子的适应度；

在路径规划问题中，移动距离最短是首要考虑的目标，因此将路径总长度作为粒子的适应度函数。

步骤3 更新个体极值和群体极值；

在每一次迭代中，粒子i在时间(t+1)速度和位置更新为式(8)、式(9)。

vid(t+1)=ωvid(t)+c1r1[Pid-xid(t)]+

c2r2[Pgd-xid(t)]

(8)

xid(t+1)=xid(t)+vid(t),d=1,2,…,D

(9)

式中,vid(t)为粒子i第d维的当前速度；xid(t)为粒子i第d维的当前位置；Pid为个体极值；Pgd为全局极值；c1、c2为加速常数；r1、r2为0～1之间均匀分布的随机数；ω为惯性权重。

步骤4 如果满足约束条件(达到最大迭代次数)进入步骤5，否则返回步骤2；

步骤5 初始化蚁群参数，使用粒子群算法得到的次优解对蚁群算法的信息素矩阵分布进行初始化[6],如式(10)。

τs=c+τp

(10)

式中，c为一个信息素常数；τp为由粒子群算法得到的初始信息素增量。将粒子群算法得到的次优解区域范围作为主要信息素分布区域，并将每一点的最佳适应度值作为蚁群算法的初始信息素增量,如式(11)。

τp=Pgd(j)

(11)

步骤6 将蚂蚁随机置于任一节点上，计算蚂蚁转移概率，并选择下一步路径；

当蚂蚁在t时刻完成检测窗ai的拍摄后，选择aj作为下一个拍摄窗口的概率，如式(12)。

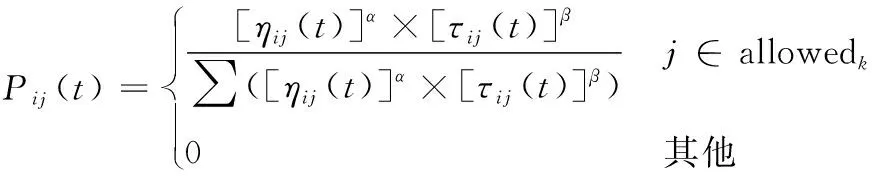
(12)

式中，ηij为由ai转移到aj的启发信息，即两检测窗的距离对蚂蚁选择的影响；τij(t)为t时刻，从ai到aj的路径上的信息素浓度；α分别为启发信息ηij对路径选择概率的影响参数；β为信息素τij对路径选择概率的影响参数；allowedk为蚂蚁k下一步允许到达的检测窗集合，在此集合中包含蚂蚁k尚未到达的所有检测窗的集合，保证所有检测窗均经历且只经历一次。

步骤7 逐次逼近调整检测窗位置；

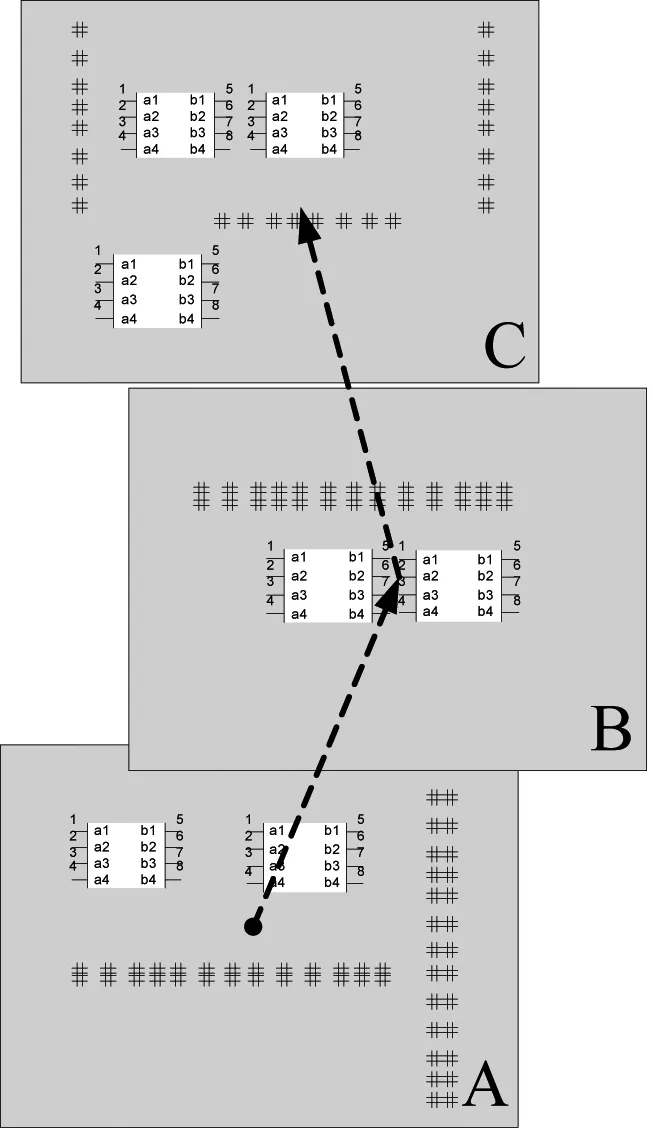
每只蚂蚁完成一次循环后，考虑本次路径中各个检测窗的可移动范围。如图3所示，若选择移动路径A-B-C，则移动检测窗B的中心位置，使A-B-C的路径最短，然后根据B-C-D来移动检测窗C的中心位置，使B-C-D的路径最短……重复直到经过所有检测窗。这样计算得到本次路径的最短距离，并用于计算更新各分支路径的信息素[3]，如图3所示。

步骤8 更新信息素浓度；

当经过n个时刻，m只蚂蚁均遍历整条路径后，更新各条路段上的信息素,如式(13)、式(14)。

τij(t+n)=ρ×τij(t)+Δτij

(13)

(14)

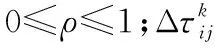
(15)

式中，Lk为蚂蚁k完成本次遍历的路径长度；Q为常数。

步骤9 如果满足约束条件(达到最大循环次数)，程序结束，输出最优解；否则返回步骤6。

3 实验仿真结果与分析

为了验证本文算法的有效性，在给定参数下进行仿真实验。相机FOV的尺寸为12 mm×10 mm，如果尺寸为226 mm×90 mm，则包含1 128个待测对象的PCB上进行测试。获取每个待检测对象的坐标信息后首先利用改进的ISODATA聚类算法进行检测窗的划分,如图4、图5所示。

图4 待检测PCB

图5 检测窗划分结果

得到检测窗划分结果之后分别采用标准蚁群算法以及本文算法对CCD的移动路径进行规划，分析算法性能的差别。在蚁群算法中，设定群体规模等于检测窗个数、启发信息因子α=1.0、信息素浓度因子β=5.0、轨迹持久性因子ρ=0.3、最大迭代次数iter=100；在粒子群与蚁群混合算法中，首先设定使用粒子群算法迭代50次得到次优解后，根据式(10)、(11)初始化蚁群算法中的信息素分布，再使用蚁群算法进行优化。

蚁群算法在第78次迭代时收敛，最短路径为14 127 mm，粒子群与蚁群混合算法在第31次迭代时收敛，最短路径为12 673 mm；同时从迭代过程可以看出，由于混合算法的信息素矩阵分布由次优解进行初始化，改善了搜索初期的盲目性，因此混合算法的起点较高。

为进一步验证粒子群与蚁群混合算法的算法性能，继续在不同规格的PCB上进行测试。

使用粒子群与蚁群混合算法可以得到最短的规划路径，而且混合算法得到最优解所需的迭代次数最少，收敛速度最快,如图6、图7和表1所示。

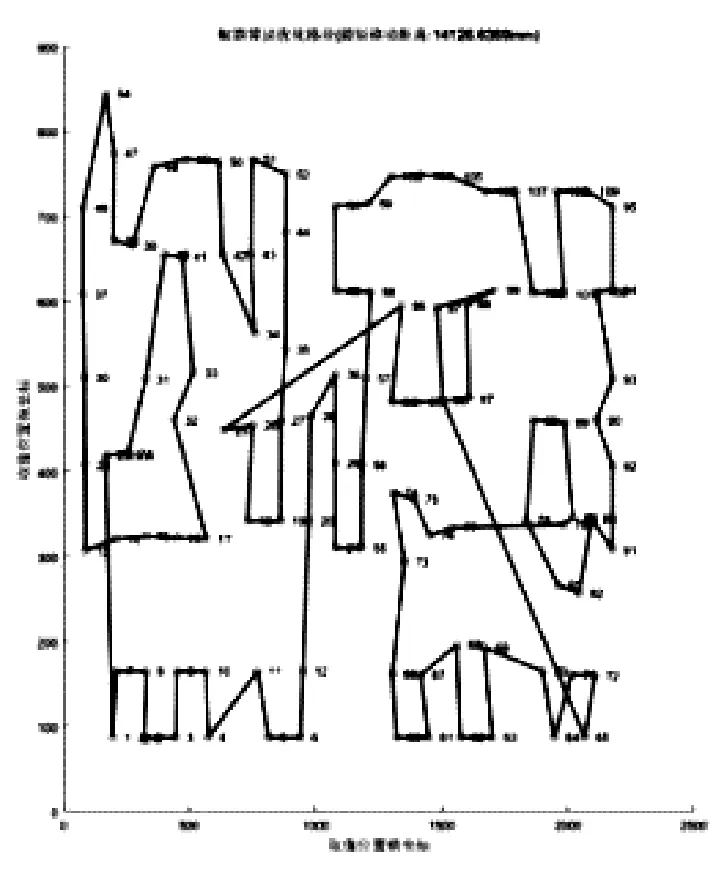
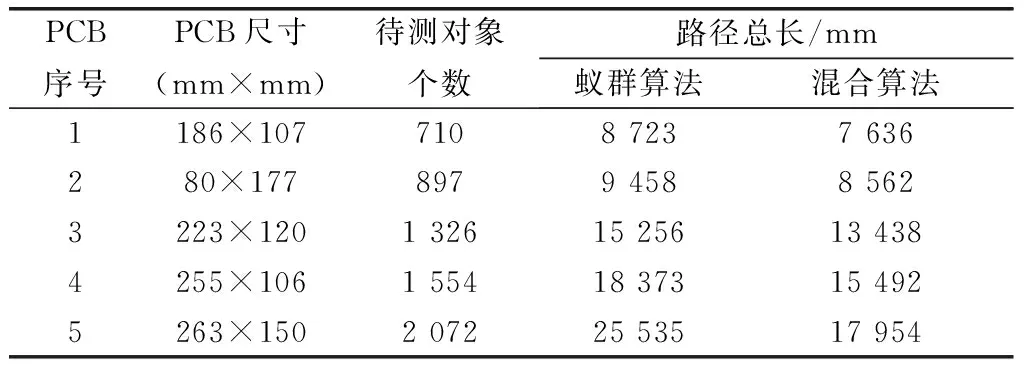
表1 取像路径优化仿真实验结果

4 总结

本文采用改进的ISODATA聚类算法进行检测窗划分，然后采用粒子群与蚁群混合算法进行取像路径的优化。在混合算法的第一阶段采用粒子群算法，利用粒子群算法前期收敛的快递性和全局性得到问题的次优解，用次优解初始化蚁群算法中的信息素分布，充分发挥蚁群算法的局部寻优能力，考虑了检测窗口的可移动范围从而缩短了路径长度。使用不同规格的PCB进行实验，混合算法在求解性能上均优于标准蚁群算法，验证了本文算法的可行性和有效性。