基于层次分析法的宏观经济指标可靠性评价
2021-06-24韩笑
韩笑
(黑龙江中医药大学 马克思主义学院, 黑龙江 哈尔滨 150040)
0 引言
随着国家经济的发展,如何保证国家经济的稳步发展以及保证宏观经济振兴的效果,需要通过对宏观经济水平作出评价来实现。因此,建立一套可靠的宏观经济指标评价体系,对于国家经济发展和监测具有重要意义[1]。相关的宏观经济指标评价研究受到人们的极大关注。目前,我国学者提出一种相关性分析的宏观经济指标预测算法,通过插值和归类等方法预处理指标数据,根据获得的时序数据进行寻优[2]。还有学者提出采用显著性差异和冗余信息剔除原则筛选指标,构建金融评估指标体系[3]。但上述方法常因指标的相关程度不同导致在时间序列中动态传导预测误差较大,而使指标评价的可靠性不足。
为解决上述问题,本文引入层次分析法构建宏观经济指标可靠性评价模型。构建宏观经济指标的描述性统计分析模型,采用面板数据检测方法进行宏观经济指标的大数据信息融合,提取宏观经济指标面板融合数据的统计特征量,通过关联规则谱分析方法进行宏观经济指标的可靠性融合和决策,建立宏观经济指标可靠性评价的模糊决策函数,通过层次分析方法进行宏观经济指标可靠性决策和层次化决策分析,实现宏观经济指标的可靠性评价。最后检验结果验证了本文方法在宏观经济指标可靠性评价中误差较小,精度较高,结果较可靠,性能较优越。
1 宏观经济指标可靠性约束指标分析和模型构建
1.1 宏观经济指标可靠性约束参量分析
为实现宏观经济指标可靠性评价,结合面板相关数据分析方法,构建宏观经济指标可靠性的约束关系模型,结合市场因素和货币因素,寻优控制宏观经济指标可靠性分析结果,构建宏观经济指标可靠性分析的约束参数模型[4],如图1所示。

图1 宏观经济指标可靠性分析的约束参数模型
根据宏观经济指标可靠性分析的约束参数模型,结合货币政策波动以及商品市场价格波动因素的联合评价方法,分析宏观经济指标可靠性[5]。经济可靠性分布的联合平均值为Cij,采用空间均衡调度方法,模糊决策宏观经济指标可靠性评价,得到全球化环境下宏观经济指标可靠性评价指标参数的模糊度函数,如式(1)。
(1)

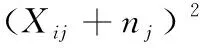
(2)
采用关联规则挖掘方法,得到宏观经济指标可靠性评价的约束参量模糊关联规则集,如式(3)。
y(e)=∑Z+lp+ε1(t)
(3)
其中,ε1(t)表示标准正态函数。
根据上述分析结果,采用自适应寻优控制,预测宏观经济指标可靠性的水平,结合特征信息聚类,提高宏观经济指标可靠性聚类水平[7],进一步提高宏观经济指标可靠性评价能力[8]。
1.2 宏观经济指标可靠性评价模型构建
采用面板数据检测方法融合宏观经济指标的大数据信息,提取宏观经济指标面板融合数据的统计特征量[9],得到宏观经济指标可靠性分布的寻优函数,如式(4)。
(4)
其中,f表示大数据信息融合参数。根据宏观经济指标可靠性评价的特征提取和面板数据寻优结果,预测宏观经济指标的波动指数[10],建立宏观经济指标可靠性评价的模糊度函数,如式(5)。
h(r)=bt+|φa+w|
(5)
其中,φa表示宏观经济指标可靠性分布式融合参数;w表示国际投资的全局效率。构建货币政策对宏观经济影响的先验分布集,结合先验知识预测宏观经济指标可靠性[11],得到宏观经济指标可靠性评价的制约参数模型,如式(6)。
p=h(r)+li+∑w
(6)
其中,li表示DCC-MVGARCH模型的聚类函数。采用货币政策的饱和度分析方法,得到宏观经济指标可靠性评价的决策函数,如式(7)。
(7)
通过上述模型,采用宏观经济指标可靠性评价的多元回归分析模型,通过非线性时间序列分析,得到宏观经济指标的可靠性层次差异迭代模糊评价模型,如式(8)。
w(i)=b+(xi,xj)+to
(8)
其中,(xi,xj)表示宏观经济指标的分布单元格;b表示宏观经济指标评价的拉格朗日算子。通过关联规则谱分析方法实施宏观经济指标的可靠性融合和决策,通过层次分析方法实行模糊迭代,建立宏观经济指标可靠性决策和模糊度函数,以期提高宏观经济指标的可靠性决策能力[12]。
2 宏观经济指标可靠性评价优化
2.1 参数寻优
分析货币政策对宏观经济指标可靠性的制约约束,结合宏观经济指标的波动特征分析方法,展开宏观经济指标可靠性评价的层次分析[13]与宏观经济指标的波动特征,根据宏观经济指标的波动幅值实施量化加权,得到宏观经济指标可靠性自适应评价的模糊加权控制函数,如式(9)。
(9)
根据经济增长的水平衡量系数,通过协方差运算,得到量化特征分布协方差矩阵,如式(10)。
(10)
其中,SR,SS和SE分别表示宏观经济指标可靠性分布的梯度分量。结合波动性影响因素实施定量分析宏观经济指标可靠性[14],得到宏观经济指标可靠性分布式约束参数模型,如式(11)。
(11)
辨识宏观经济指标可靠性参数,得到宏观经济指标可靠性评价参数的寻优控制模型,如式(12)。
C=∑U+v(j)+qc
(12)
采用最大Lyapunov参数寻优控制的方法,实施并得到宏观经济指标可靠性决策,通过自相关映射和特征寻优,得到宏观经济指标可靠性参数,提高宏观经济指标可靠性评价的准确性。
2.2 可靠性评价决策
将宏观经济指标可靠性变量定义为Zi(i=1,2,…,8),得到约束宏观经济指标可靠性的市场敏感性特征量,通过成本约束和代价函数分析方法,得到宏观经济指标可靠性分布的加权系数为Wki(i=1,2,…,8;k=1,2,…,8),制约宏观经济指标可靠性的基础货币增长率定义为Xij(i=1,2,…,6;j=1,2,…,8),构建SPSS统计分析模型,得到宏观经济指标可靠性评价的统计特征量,如式(13)。
E=Zi+Wki+Xij
(13)
分析观测变量的面板数据主成分,建立宏观经济指标可靠性分布的最大似然函数,得到宏观经济指标可靠性决策的层次化分析标准量化参数,如式(14)。
(14)
结合货币差异性评价[15]和市场因素流动性波动分析方法,进行宏观经济指标可靠性的评价,得到评价决策的拟合函数,如式(15)。

(15)
综上分析,建立宏观经济指标可靠性评价的模糊决策函数,通过层次分析方法进行宏观经济指标可靠性决策和层次化决策分析,最终实现宏观经济指标的可靠性评价决策。
3 实证分析
为量化分析宏观经济指标可靠性,采用SPSS统计分析软件,统计分析国家发布的2018年全国经济数据与2019年全国经济数据,设置数据采样的长度为1 024,迭代次数为500,以经济增长水平和市场投资水平为自变量,得到描述性统计分析结果,如表1所示。
由表1的分析结果进行宏观经济指标可靠性评价决策,得到宏观经济指标可靠性评价的分布模型,如图2所示。
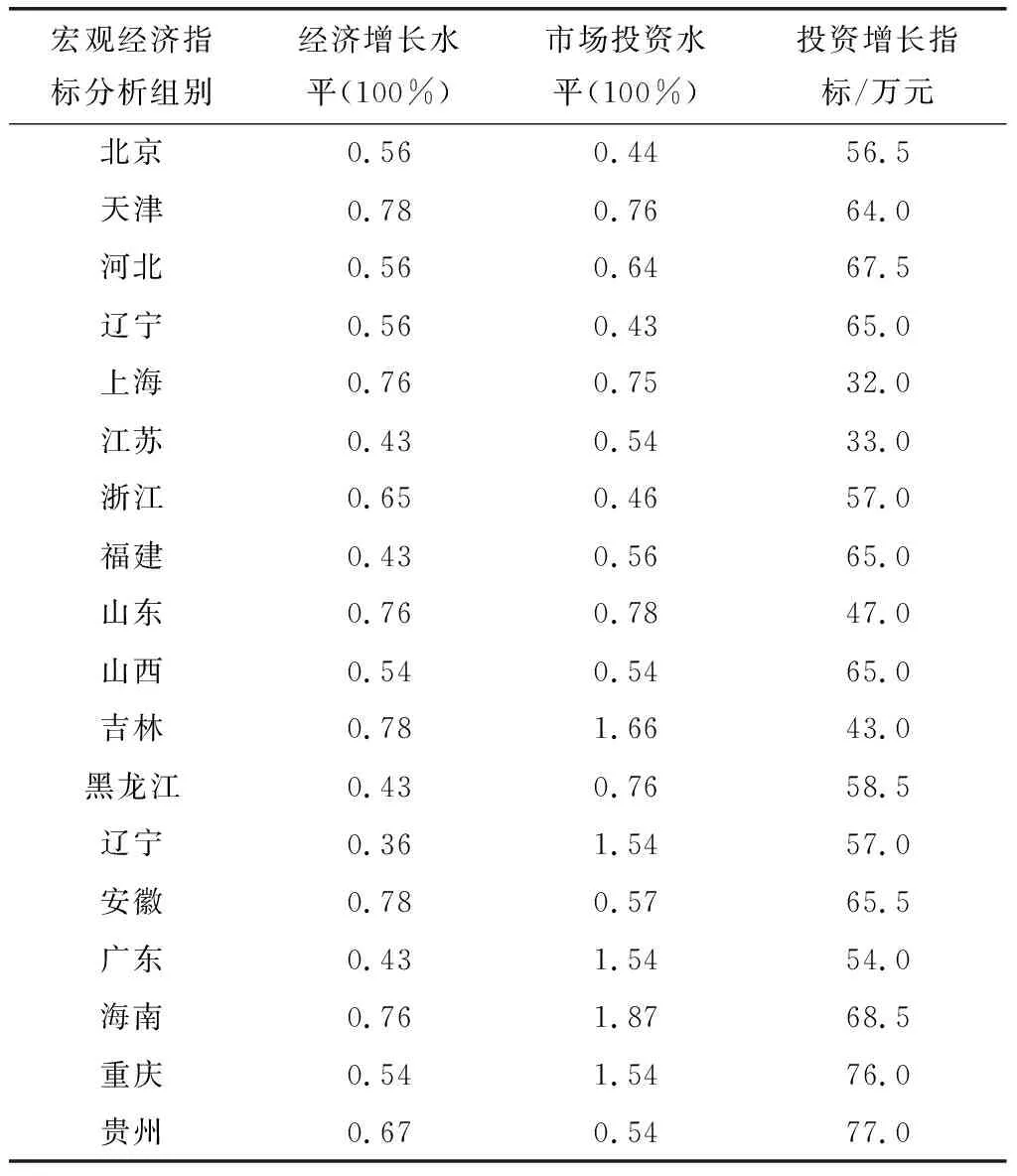
表1 描述性统计分析结果
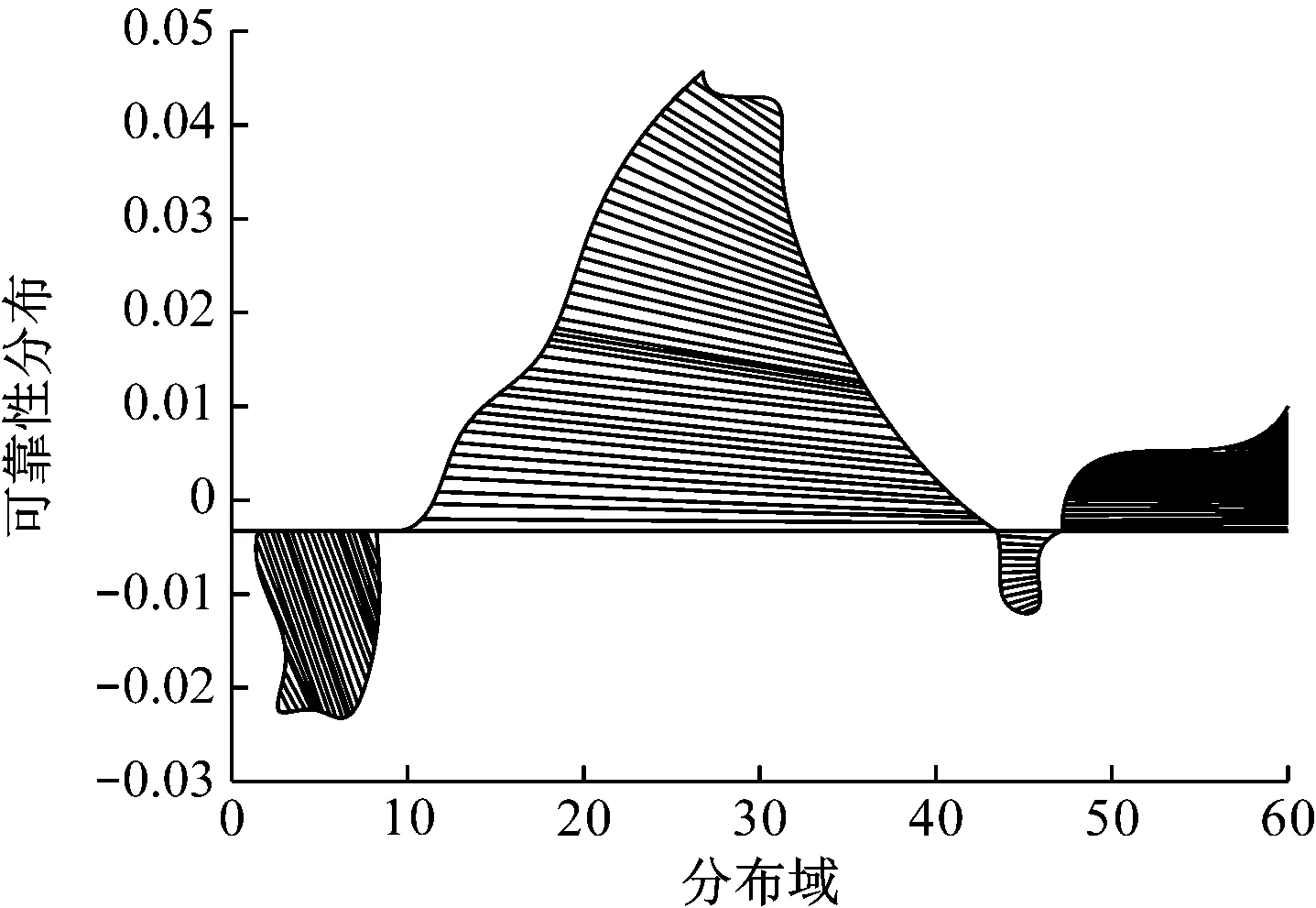
图2 宏观经济指标可靠性评价的分布
由图2可知,P<0.05,有统计学意义,因此本文方法能有效实现对宏观经济指标可靠性评价。测试宏观经济指标可靠性评价的变异系数(标准差/平均值)和绝对差率(各指标最小值/各指标最大值),所得结果如图3所示。
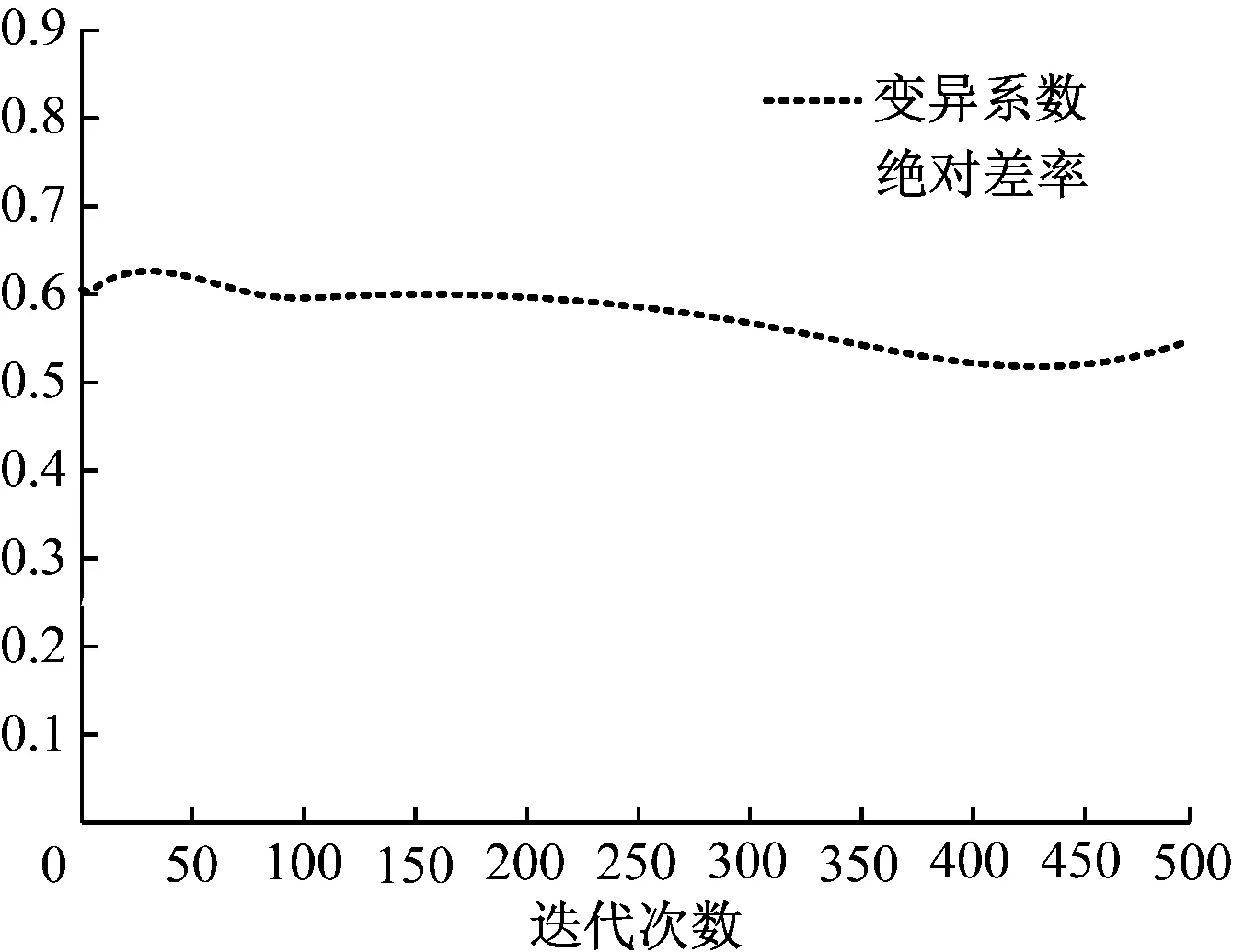
图3 宏观经济指标可靠性评价的收敛性测试
由图3可知,以本文方法进行宏观经济指标可靠性评价的各指标变异系数总体上在0.58上徘徊,绝对差率也大致稳定在0.2附近,波动幅度都不大,说明本文方法的评价误差可控。
为验证本文方法的优越性能,采用文献[2]方法、文献[3]方法与本文方法分别验证2018年和2019年宏观经济指标指数的实际值与预测值,如表2所示。
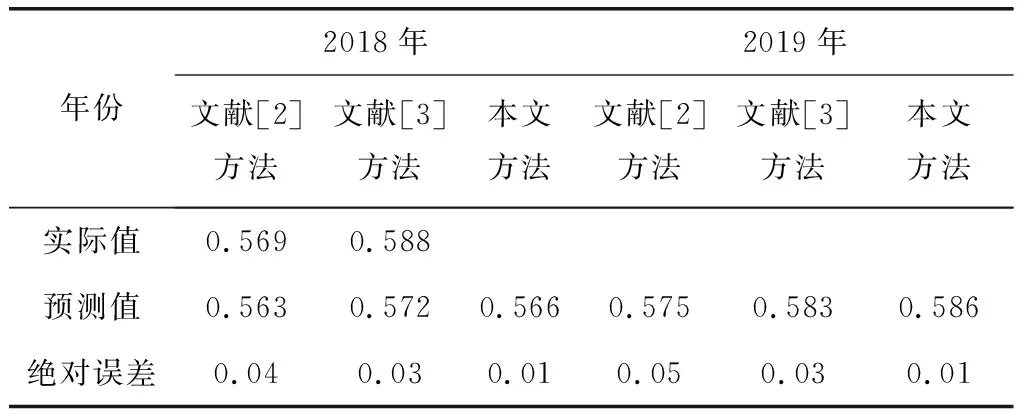
表2 2018—2019年预测验证结果
由表2可知,本文方法的预测值与实际值较接近,绝对误差保持在0.01,与传统方法相比,误差较小,精度较高,结果较可靠。
4 总结
本文根据市场因素和货币因素,建立了一个科学合理的,能全面反映宏观经济总体情况的宏观经济指标可靠性分析模型。采用面板数据检测方法进行宏观经济指标的大数据信息融合,提取宏观经济指标面板融合数据的统计特征量,通过关联规则谱分析方法进行宏观经济指标的可靠性融合和决策,建立宏观经济指标可靠性评价的模糊决策函数。分析得知,本文方法对宏观经济指标可靠性决策评价的准确性较好,结果较可靠。本文方法可在一定程度上提高宏观经济指标的可靠性决策能力,以期推动国家经济发展。
