基于深度神经网络的电力变压器故障诊断
2021-06-24邓燕山赵凯利吕文超白杰董杰高岭
邓燕山, 赵凯利, 吕文超, 白杰, 董杰, 高岭
(国网冀北电力有限公司唐山供电公司, 河北 唐山 063000)
0 引言
溶解气体分析法(DGA)是诊断电力变压器故障的常见方法[1]。DGA的原理是故障电力变压器在热应力和电应力作用下,其油纸绝缘层会分解出可溶解的气体,通过气体分析可以诊断变压器的故障类型[2]。本文将使用深度神经网络算法(DNN)对溶解气体数据进行挖掘分析,以实现变压器故障的自动分类。
DNN需要大量数据进行监督学习。为了降低对高可用性数据的依赖,本研究将使用杜瓦尔三角法生成模拟DGA数据,并将其应用于DNN训练中。为了证明DNN在电力变压器故障诊断应用中的有效性和性能,本文针对分类准确性将DNN与随机森林分类算法(RFC)、K最近邻分类算法(KNN)进行了对比测试。
1 机器学习算法
1.1 KNN算法
KNN算法是简单的且广泛使用的监督聚类算法之一。其主要思想是通过数据点之间距离的计算,实现对未分类的数据进行分类。k是最近数据点的数量。对于每个未分类的点,该算法将计算其与k个最近的数据点之间的距离,如图1所示。
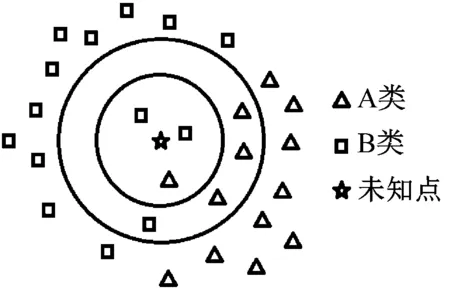
图1 KNN算法
如果k设置为3,则未知点将归为B类,因为三个最近点中的两个属于B类;如果k设置为7,则未知点将属于A类,因为属于A类的点最近。
KNN算法通常会产生一致的结果,并且计算过程较简单[3]。但是,该算法的效率会随着数据量的增大而大幅下降[4]。
1.2 随机森林分类算法(RFC)
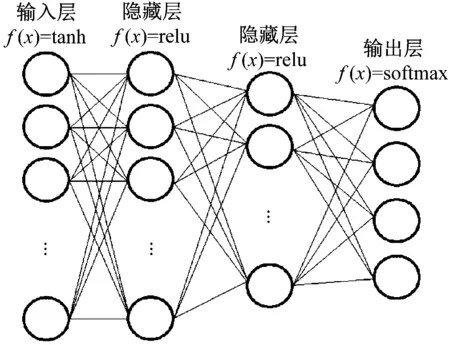
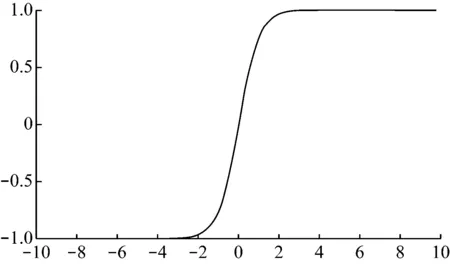
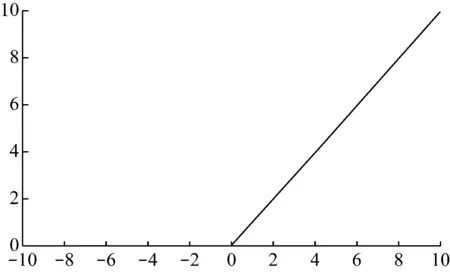
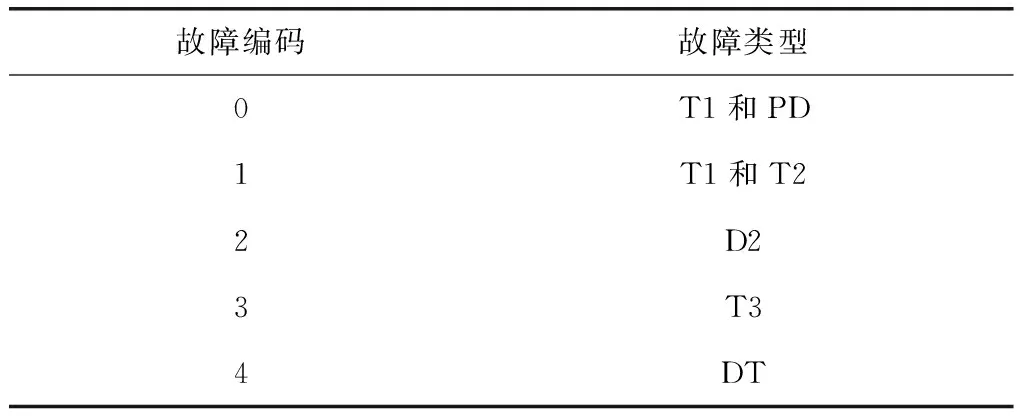
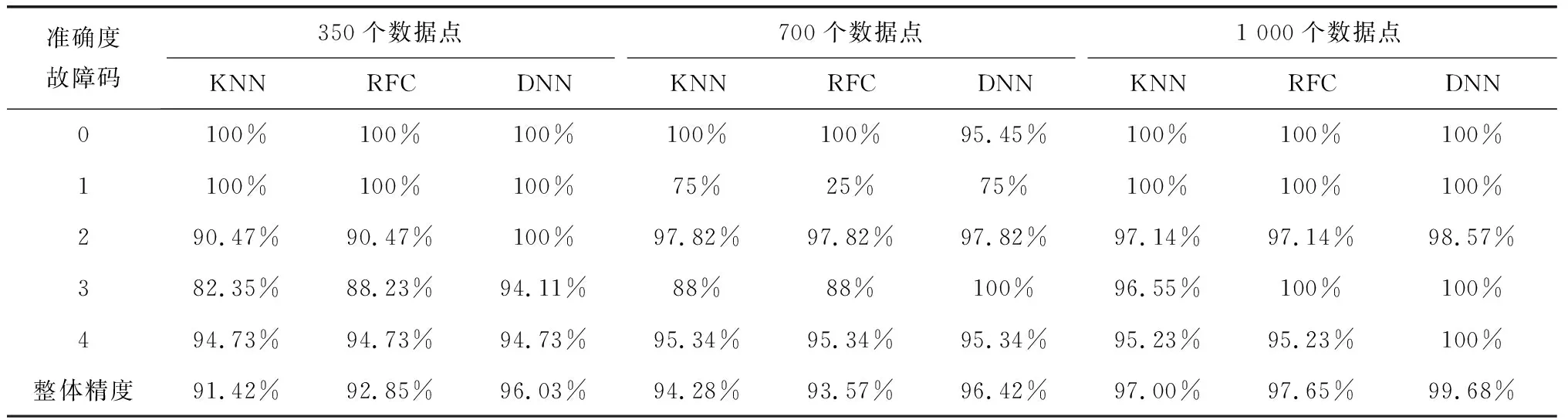
RFC是一种监督聚类算法。该分类算法由多个决策树组成,这些决策树用于对未分类的数据集进行分类。每个决策树都是一个分类器。如果有N个训练数据,则在训练过程中,随机替换M个训练数据(M 神经网络是从生物神经元结构衍生而来的抽象和简化模型。通常,神经网络模型由输入层、隐藏层和输出层组成。每层中的节点都模仿神经元,节点之间使用不同的权重进行连接[7]。 神经网络算法的过程包括输入数据正向传播和误差反向传播。在正向传播中,原始数据从输入层传输到隐藏层,隐藏层使用激活函数提取数据的特征。激活函数的目的是通过加权输入的非线性组合产生非线性决策边界。输出层完成分类过程[8]。在误差反向传播中,该算法利用监督的分类结果并修改神经元连接的权重[9]。 DNN由多个隐藏层组成,如图2所示。 图2 神经网络 每个层都应提取不同级别的数据特征。分类器包含两个隐藏层。输入层的激活函数为tanh,两个隐藏层的激活函数为ReLU,输出层的激活功能为SoftMax。 tanh函数将实数值映射到[-1,1]范围,如图3所示。 图3 tanh函数图形 ReLU函数的计算式为f(x)=max(0,x),如图4所示。 图4 ReLU函数图形 与tanh函数相比,ReLU函数的优点之一是极大地加快了随机梯度下降的收敛速度[10]。因此,将两个隐藏层的激活函数选择为ReLU。Softmax(归一化指数函数)函数[11]的计算式为式(1)。 (1) σ(z)是输出向量,zj是输入向量z的元素,如图5所示。 图5 Softmax函数图形 在反向传播过程中,本研究使用Adam优化方法更新网络权重。相对于随机梯度下降优化方法,Adam优化方法可以根据梯度的第一和第二矩的估计来计算不同参数的单独学习率。经验结果表明,Adam优化方法在实践中比随机梯度下降方法效果更好[12]。 常见的分析变压器油中所溶解气体的方法有关键气体法、Rogers比率法、Doernenburg比率法和杜瓦尔三角法[13-14]。通过338个油样的对比试验表明,与其他溶解气体分析方法相比,杜瓦尔三角方法具有最高的一致性。 因此,在本研究中随机生成大量的气体化合物百分比数据,并使用杜瓦尔三角法生成相应的故障类型。这些模拟数据分为用于深度神经网络模型的训练数据集和测试数据集。杜瓦尔三角分析法如图6所示。 图6 杜瓦尔三角 杜瓦尔三角故障区域如表1所示。 表1 杜瓦尔三角故障区 实验首先是随机生成包含三种气体的数量的1 000个数据点的数据集,并使用杜瓦尔三角方法确定相应的故障类型。从故障变压器历史数据得出的最小值和最大值边界,以确保所生成的数据样本落在经验值边界之内。三种溶解气体为CH4、C2H2和C2H4,它们各自的百分比为三种气体占气体总量的比例。由于某些故障类型的发生概率较低,本实验将七种故障类型组合为五种:低能放电(D1和PD)、高能放电(D2)、最高700℃的发热故障(T1、T2)、高于700℃发热故障(T3)以及热电故障(DT)。每个样本的故障类型编码都为0到4之间的整数,如表2所示。 表2 故障编码 为了测试数据大小的影响,实验采用生成的数据集的子集的方式来形成其他数据集。具体而言,创建分别具有350、700和1000个数据点的三个数据集。对于这三个数据集的每一个,将80%的数据点用作训练数据集,并将其余的数据点(20%)用作测试数据集。实施的DNN模型的每一层中的节点数分别为256、126、32和5。实验首先以10-3的学习率训练网络,然后将其更改为10-5进行测试。深度神经网络的参数如表3所示。 表3 DNN参数 基于表3指定参数,深度神经网络模型(DNN)在具有1 000个数据点的数据集上实现了99.68%的精度。实验还使用相同的数据集测试了KNN和RFC。KNN算法的准确率为97%,而RFC为97.65%。 为了检查数据大小对准确性的影响,实验采用了三种不同大小的数据集,这三个实验过程的准确性如表4所示。 表4 每种故障类型与整体精度的准确性比较 从表4可以看出,随着数据点数量的增加,实验的准确性都会提高。实验结果可以总结如下:(1) 数据集越大,每种方法在电力变压器故障识别应用中的总体精度就越高;(2) 测试结果表明,与KNN和RFC方法相比,DNN具有更高的识别准确性。 本文使用DNN来识别变压器的故障类型。在本研究的实验中随机生成数据点,并使用杜瓦尔三角法确定用于监督学习的故障类型。DNN被设计为具有四层的网络结构,其激活函数分别是Tanh、ReLU和SoftMax。权重更新使用Adam优化器。试验结果表明,与KNN和RFC相比,DNN在识别变压器故障类型方面具有更高的准确性。1.3 深度学习网络
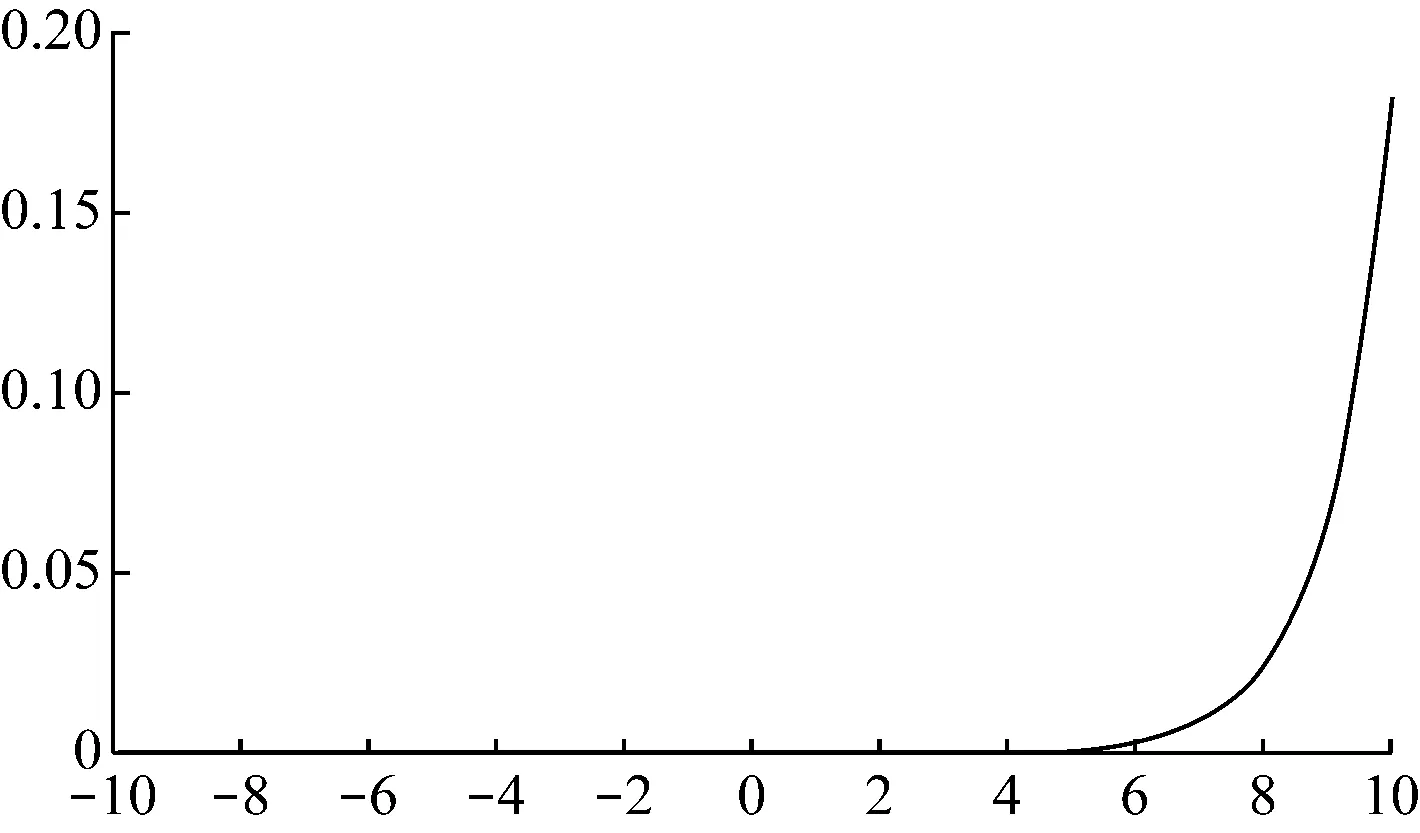
2 采用杜瓦尔三角生成仿真数据
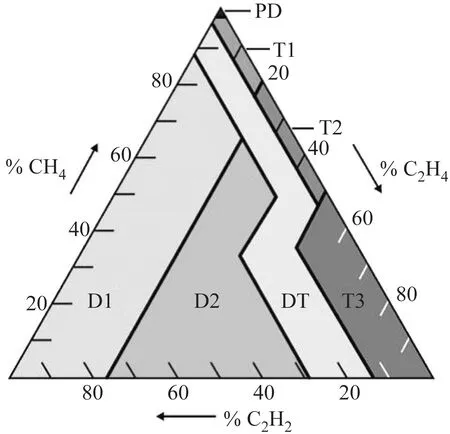
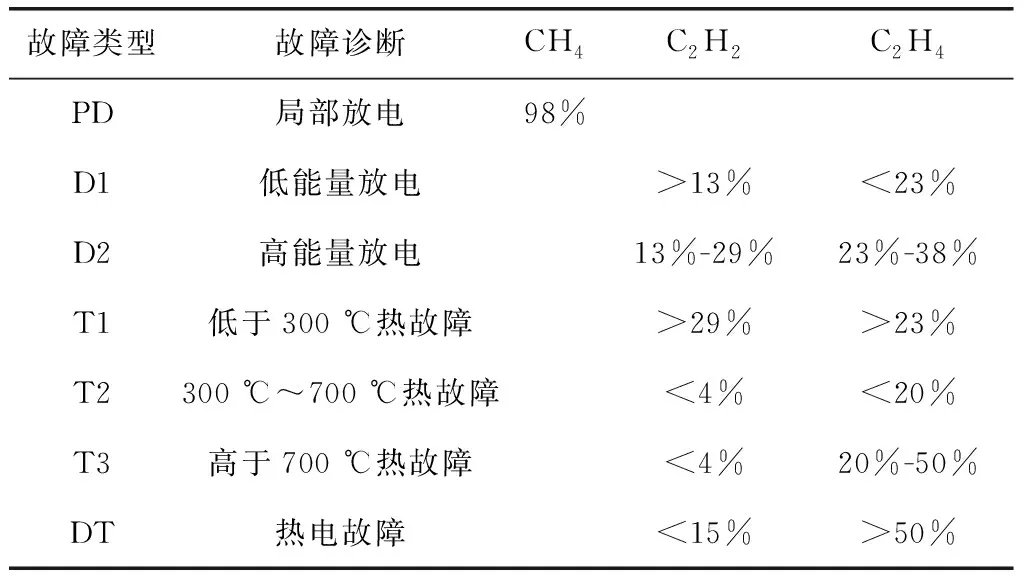
3 实验验证

4 总结
