变频调速系统电磁干扰主要影响参数

曹海洋， 余志洪

（1.中国矿业大学电气与动力工程学院，江苏徐州 221116；2.江苏省电力传动与自动控制工程技术研究中心，江苏徐州 221116）

0 引 言

变频设备中的开关器件均工作在开通和关断状态下，该特性决定了IGBT等开关器件在开通关断时会带来较大的功率、电压和电流并且会在电路里面产生较大电压跳变以及电流纹波，使电路中电压，电流包含大量的高次谐波，引起很大的电磁干扰［1-5］。电磁干扰的预测需要在设计阶段建立干扰耦合路径模型，搭建精确的路径模型需要获取各个寄生参数的值以及系统整体的特性，这样需要耗费大量时间和精力［6-10］。本文研究的对象是兆瓦级变频调速系统，如果全盘考虑系统所有的寄生参数，由此建立的模型将会相当复杂，甚至有可能导致建模失败。本文基于巨变灵敏度的思想对预测模型进行化简，删除对电路干扰影响程度较小的寄生参数支路，极大地简化了变频器调速系统预测模型。本文通过实验，将简化模型计算出的传导电磁干扰与实验结果进行对比，验证了理论分析和预测模型的准确性。

1 基于高压探头三电平变频器传导EMI路径分析

电磁干扰路径是指噪声从干扰源到敏感设备之间的流通路径，传导干扰分为共模干扰和差模干扰［11-14］，以电压或电流形式在干扰路径中流通，由于测试是基于电压探头的，故分析干扰路径时也是基于电压探头进行分析，双三电平调速系统干扰流通路径如图1所示，其中功率开关器件产生的d u／d t会在耦合电容中产生共模干扰电流，如图1中红色虚线所示，主要在相线／中线-地线之间流动；差模干扰主要由功率开关器件开通关断过程中产生的d i／d t在系统线路中的寄生电感上感应出很大的差模电压，形成噪声发射，在相线间流通，如图1中蓝色虚线所示。

图1 变频调速系统传导电磁干扰路径

2 基于高压探头三电平变频器传导EMI模型建立

根据第1节中对传导电磁干扰路径的分析，可以得到基于电压探头传导EMI模型如图2所示。

图2中的干扰源为载波同相层叠时三电平空间矢量脉宽（Space Vector Pulse Width Modulation，SVPWM）调制策略下的干扰源模型，载波的频率设置为2 kHz，调制波的频率设置为50 Hz，调制度为1。其中：U1为整流侧的干扰源；U2为逆变侧的干扰源；Lc1、Rc1、Lc2、Rc2分别为变频器长度为1 m的输入电缆和长度为10 m的输出电缆的等效电感和等效电阻；L、Ri、Ci分别为电抗器、其等效损耗电阻和匝间寄生电容；Ls1、Rs1、Ls2、Rs2分别为直流母排的等效寄生电感和电阻；Cig、Cip、Cs、Cc、Cg分别为电抗器、变频器开关器件IGBT、直流母排、输出电缆和异步电动机单相绕组的对地寄生电容；Zm1为定子单相绕组的阻抗，Zm1＝(Rω＋jωLω－j/ωCω)//Re//jωLd；C、R、Rb用来模拟电压探头测试电路。

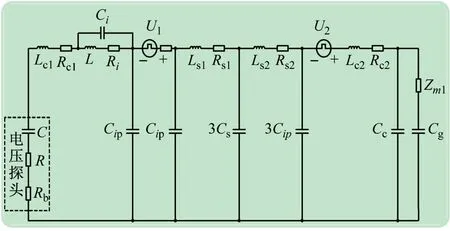
图2 基于高压探头的变频调速系统EMI高频模型

3 基于巨变灵敏度分析的传导干扰模型简化

灵敏度的概念源于电子电路设计领域，经典电路理论给出的参数y对参数x的灵敏度为：

式中：y为电路系统的某项性能指标，比如电路的电压或电流；x为电路中某个组成元件的参数［15］，如阻抗。由此可见，灵敏度的思想是用偏导数来反映控制对象某个参数改变对系统某项性能参数的影响，这一思路也是适用于传导EMI研究的。

为方便对寄生参数进行巨变灵敏度分析，对于图2中元件做适当的修改，将干扰源模型由电压源U1、U2变为电流源I1、I2与电阻并联的形式，其中与电流源I1、I2并联的电阻分别为：R5＝R8＝1Ω。其余元件的对应关系以及仿真参数为：L1＝Lc1＝0.38μH、L2＝L＝0.7 mH、L3＝Ls1＝22.5 nH、L4＝Ls2＝22.5 nH、L5＝Lc2＝3.8μH、R1＝R＝1.45 kΩ、R2＝Rb＝50Ω、R3＝Rc1＝80 mΩ、R4＝Ri＝0.39Ω、R6＝Rs1＝1.7 mΩ、R7＝Rs2＝1.7 mΩ、R9＝Rc2＝0.8 mΩ、C1＝C＝1.25 nF、C2＝Ci＝181 pF、C3＝Cig＝53.85 pF、C4＝Cip＝2.5 nF、C5＝3Cs＝15 nF、C6＝3Cip＝7.5 pF、C7＝Cc＝8 nF、Z0＝Zm1＝ (Rω＋jωLω－j/ωCω)//Re//jωLd、Rw＝10.3Ω、C8＝Cg＝195.8 nF、Lw＝1.66μH、Cw＝8.61 nF、Re＝145Ω、Ld＝0.185 mH、C8＝195.8 nF。修改后得到的传导干扰预测模型如图3所示。

图3 用于灵敏度分析的干扰模型

对图3所示节点列写方程为：

将节点电压方程表示成矩阵形式Y0X0＝W0。其中：

根据图3可知，干扰电压即为高压探头在电阻R2上的分压，所以干扰电压为：

式中，

由式（2）可以看出，系统是7×7阶，以寄生电容C3、C4、C5为例，进行灵敏度分析，由节点导纳矩阵可以得到接入矩阵P和QT，且Q＝PT，

设C3、C4、C5的变化量为ΔC3、ΔC4、ΔC5。设对角阵为：

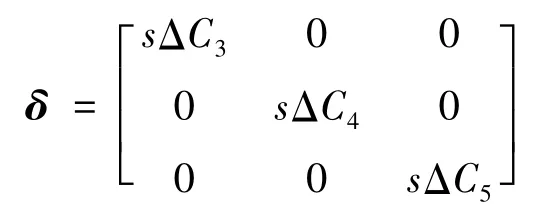
则新的系统方程可以表达为：

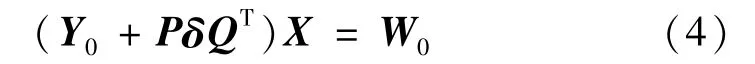
在式（4）中引入y＝QTX，z＝δQTX可以得到X的表达式。由此得到此时的差模电压表达式为：

由式（6）可以得到任意元件的灵敏度数值，依据化简原则进行电路简化。下面以电容C3为例，分析其对系统产生传导EMI的影响大小，其灵敏度仿真结果如图4所示。

图4 电容C3的巨变灵敏度曲线

图4（a）中，红色、蓝色、黑色曲线分别为电容C3减小至×10－3、×10－2和10－1倍时的灵敏度曲线，在100～10 MHz之间的灵敏度幅值均没有超过1 dB。图4（b）中，红色、蓝色、黑色曲线分别为电容C3增加至103、102和10倍时的灵敏度曲线，可以发现电容C3增大至102倍时，其灵敏度的幅值在1 MHz附近就已经接近5 dB，根据巨变灵敏度简化原则，可以对电容C3进行开路处理。其余高频参数的巨变灵敏度曲线可以通过同样的方法得到，具体情况见表1。

通过以上分析可以得到基于巨变灵敏度分析后的共模干扰简化电路，如图5所示。

图6为当模型中所有参数化简后的灵敏度曲线，可见，简化电路的灵敏度绝对值均小于1 dB，说明对模型按上述方法进行简化没有较大的影响模型的精度。

图5 干扰简化等效电路

表1 干扰模型参数简化表

图6 最终简化电路的灵敏度

4 实 验

本文的实验平台由10／1.14 kV变压器、电源滤波器、电抗器、兆瓦级双三电平变频器、2 MW对托平台及相关传导EMI测试设备组成，其中传导EMI测试设备包括电压探头、限幅器和EMI接收机，具体传导EMI测试的电气连接如图7所示。在对传导干扰进行测量时利用10 kV高压探头，并依据国标GB12668.3。其具体放置位置如图8所示。

实际测得的干扰电压频谱与利用基于巨变灵敏度方法得到的最简模型仿真得到的干扰电压频谱如图9所示。由图9分析可知，150 kHz～10 MHz内两者吻合得较好，误差在5 dB左右；10～30 MHz两者虽然存在一定误差，其原因是由近场耦合以及双重傅里叶理论本身的局限性造成，由此可以说明巨变灵敏度方法可以简化干扰模型并同时可以保证预测结果的精度。

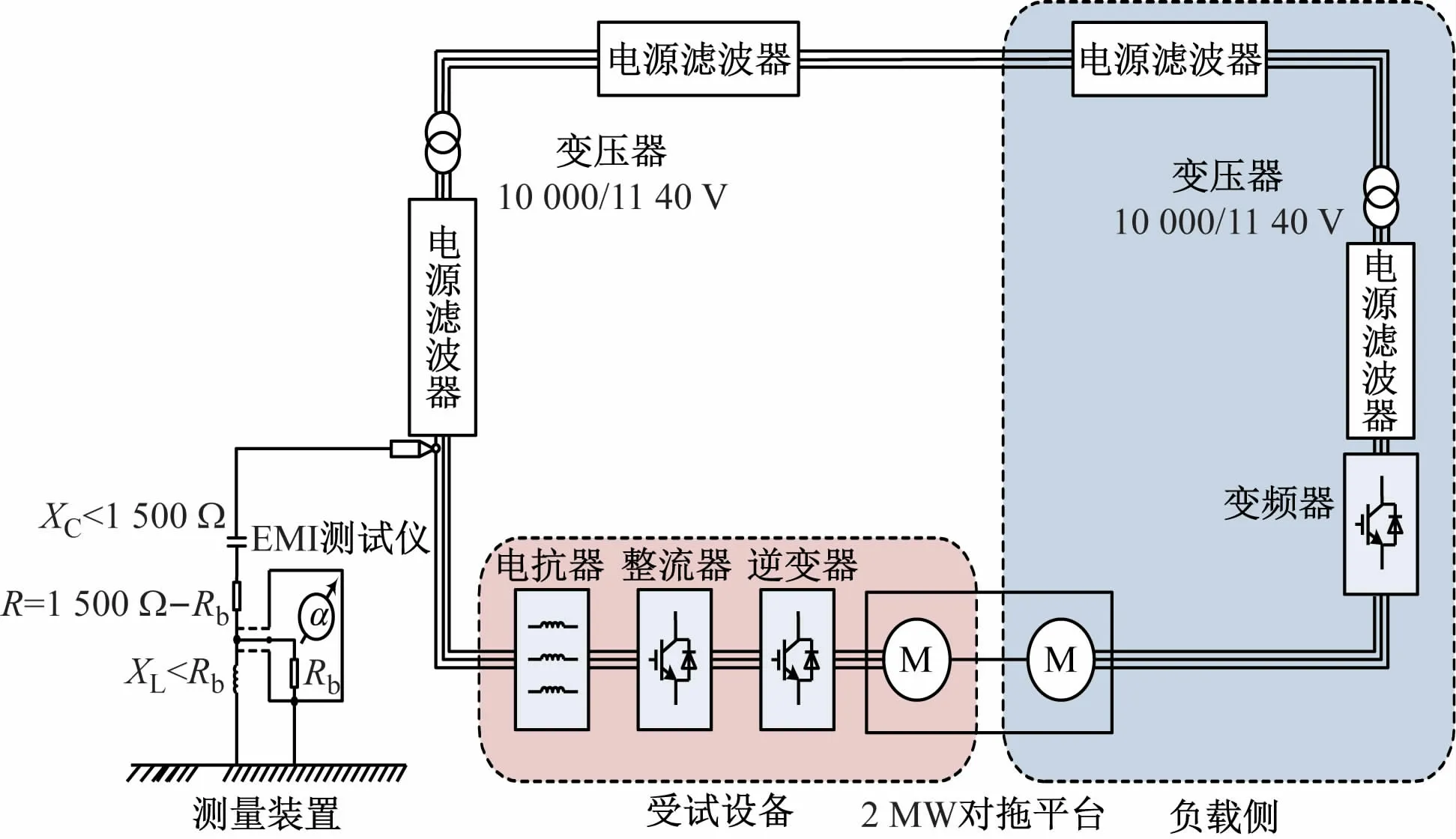
图7 传导EMI测试的电气连接图

图8 高压探头测试干扰电压位置

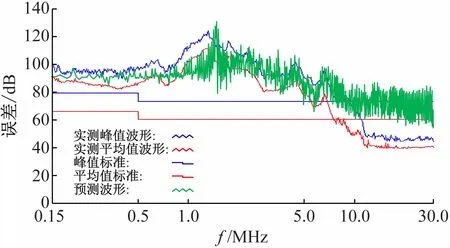
图9 预测与实测结果对比

5 结 语

本文通过对兆瓦级双三电平变频器进行巨变灵敏度分析可知，滤波器电感、IGBT与散热器间寄生电容、母排以及出线电缆对地寄生电容等元件对整体电磁干扰有很大影响，而各个元件的寄生电阻对整体电磁干扰影响很小，可以忽略，最终得到频域简化模型，该模型在反应干扰耦合路径上更加直观，并且通过与实验对比，验证了简化电路的正确性。研究结果对产品电磁兼容特性的优化设计提供了较好的指导。