盾构下穿对既有地铁隧道的影响规律数值模拟

肖自卫 张盛红

(1.中铁南方投资集团有限公司，广东 深圳 518000；2.亚热带建筑科学国家重点实验室(华南理工大学)，广东 广州 510640)

0 引言

随着中国城市化的快速推进，城市人口流入规模也在不断扩大。城市地铁作为一种城市交通的重要手段，得到了快速发展的同时也出现了许多问题。由于城市地铁的数量不断增加，不可避免地会遇到新建地铁下穿运营期地铁线路的情况，由于新建隧道会对既有隧道周围土体造成扰动，容易使既有隧道产生较大变形，因此得到临近隧道施工对既有隧道的变形影响规律具有重大工程意义。

目前，盾构隧道下穿施工对既有隧道影响的相关工程问题已经有了一些相关研究。在数值分析方面，Liu[1]研究了多种形式开挖情况下上覆隧道的内力计算方法；Wang等[2]利用数值软件建立三维盾构下穿施工模型，得到了潜在影响因素对管线变形的影响。在物理模型试验研究方面，Marshall[3]利用试验手段对下穿隧道开挖对既有管线变形特性的影响特性展开探索。同时下穿诱发的变形也被现场试验手段展开研究(Liao[4]、金大龙[5])。

上述研究得到的结论只适用于某一工程或地区,无法推广到其他工程中。基于此，本文通过数值仿真的方法，以某实际下穿隧道工程为背景，研究既有隧道变形特性的影响规律，研究成果可供类似工程借鉴。

1 工程概况

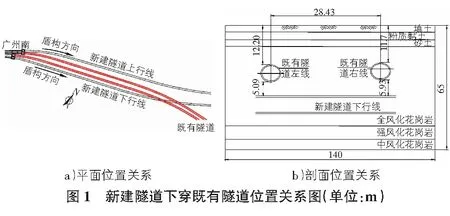
本文依托工程位于广州南站附近，原计划由新建隧道先行施工上跨穿越既有线路，由于工期延误，新建隧道下行线需两次下穿已建城际隧道，两隧道相交角度约24°斜。新建隧道采用直径为9 139 mm的土压平衡盾构法施工，衬砌外径8.8 m，内径8.0 m，环宽为1.8 m；既有隧道衬砌内外径7.7 m 和8.5 m，两相距28.43 m(轴心距离)，上覆土层厚约为12 m，两隧道最小净距5.07 m。具体工程概况如图1所示。

区间场地为珠三角平原地貌，按照土层结构及分布情况，大致可分为6层，新建隧道盾构穿越的主要地层为全风化花岗岩。

2 盾构下穿施工模拟

2.1 三维有限元模型

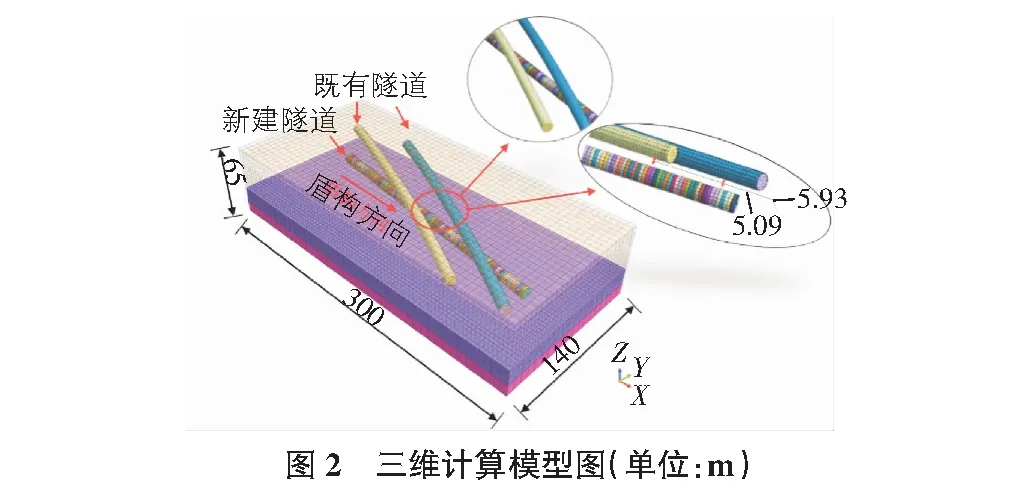
本文采用有限元软件Midas GTS对依托工程进行建模计算，通过前人研究以及建模分析，发现地下隧道开挖后的应力、应变，仅在距离隧道中心点3D～5D隧道直径范围内存在影响[6]。为减少边界效应影响，确定模型整体尺寸为300 m(长)×140 m(宽)×70 m(高)。模型边界条件为：底面固定Z方向、四周约束法线方向，三维计算模型图如图 2所示。本文采用刚度迁移法与生死单元模拟盾构开挖卸载释放地应力过程[7]。盾构开挖引起的地层损失使用位移收敛法中的圆环均匀收敛模拟[8]。模型总计138 757个单元。

2.2 模型参数的选取

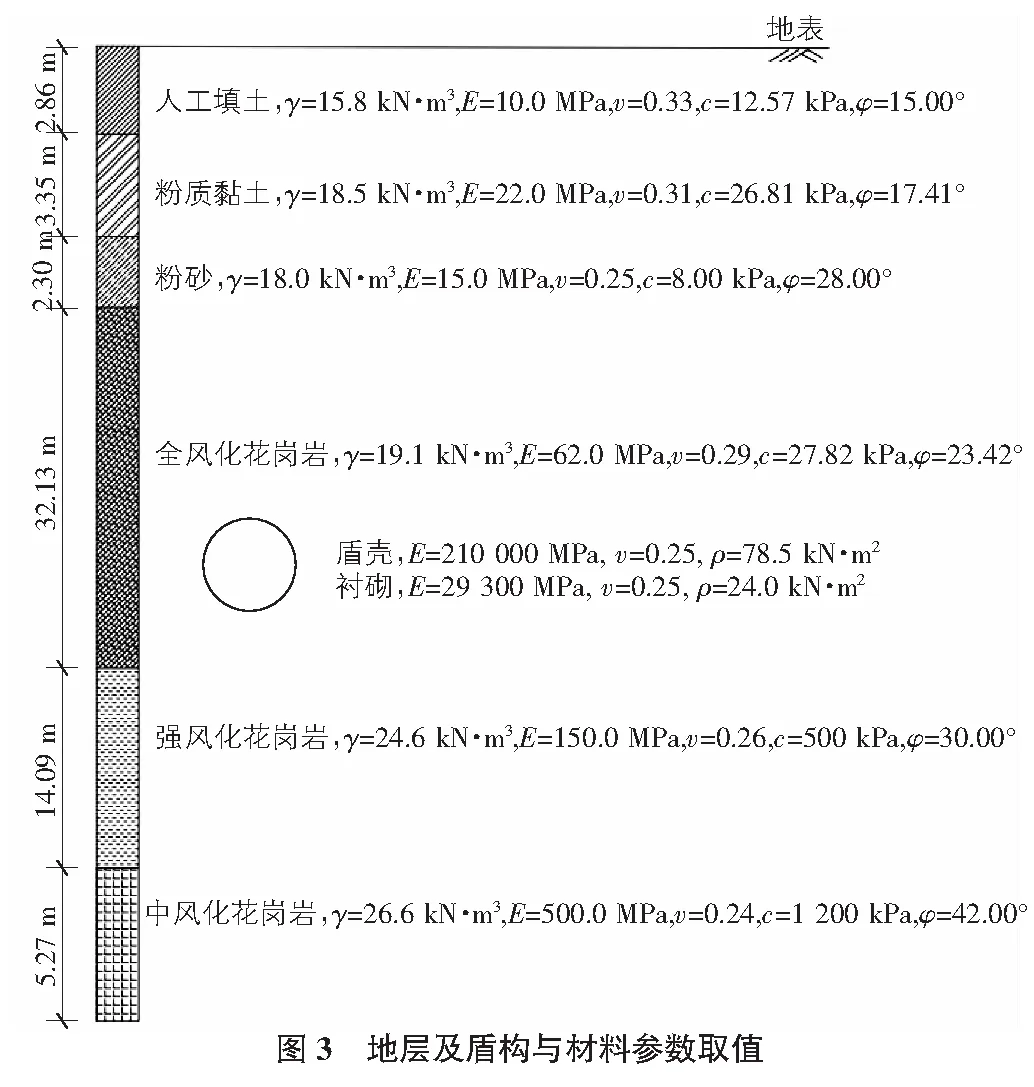
假设所有材料均为各向同性，土体采用三维实体单元模拟，服从Drucker-Prager弹塑性屈服准则。不考虑盾构机的内部构造，盾壳、管片使用板单元模拟，假定为完全线弹性材料。盾壳的强度参数与钢材参数一致；衬砌，弹性模量E取3.45×104MPa(C50混凝土)，由于其错缝拼接，弹性模量折减因子为0.85，地下水位为地表以下3 m，具体模型计算参数如图 3所示。

2.3 盾构开挖仿真

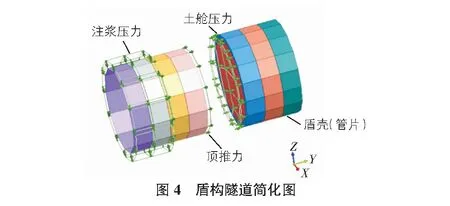
实际工程中盾构机掘进是一个连续的过程，有限元模拟可将掘进过程分解成若干相互衔接的施工步，通过激活、钝化的方法来模拟每个施工步内盾构开挖过程(见图 4)。整条新建隧道的开挖过程总共由67个施工步组成，每次掘进长度为两个环距离，约为3.6 m，模拟盾构机在实际盾构推进过程中连续动态开挖过程。

2.4 现场测点布置

通过对已建隧道盾构下穿施工段现场的地表沉降进行监测，可以得到新建下行线施工过程中施工场地的土体沉降以及临近构筑物的位移变形大小(见图 5)。分别在既有隧道以及新建隧道附近设置两个监测断面，纵向地表监测点两两间距为10 m；横向监测点彼此间距为6 m。断面2的测点布置相对距离与断面1大致相同。

3 下穿施工的三位有限元数值模拟分析

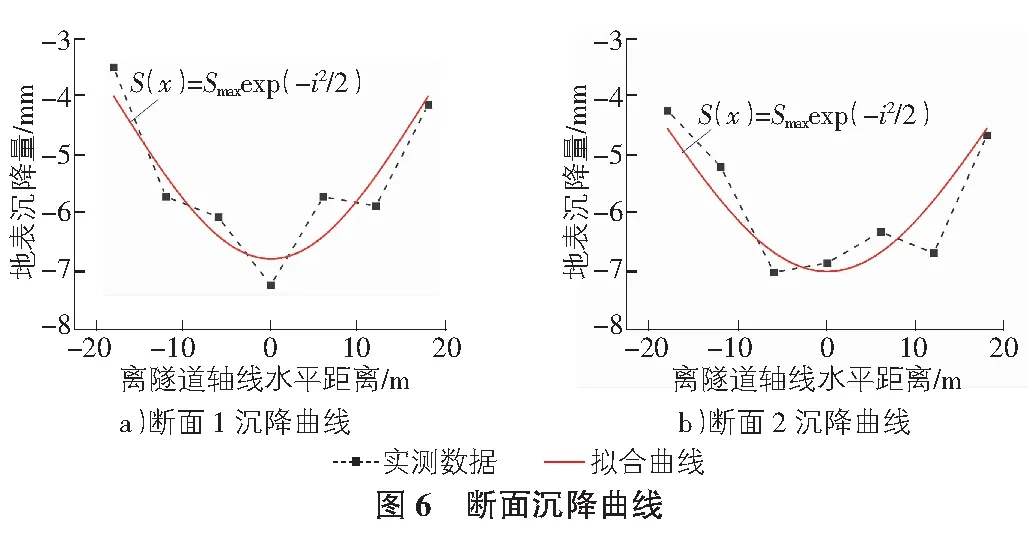
盾构施工产生的地层损失为实际开挖土体体积与建成的隧道体积(包括注浆体积)之差[8]。本文执行位移收敛方法仿真盾构施工引起的地层损失[9]。该工程的地层损失率η由断面1、断面2的实际地表沉降得到，如图 6所示，经过Peck公式(式1)反算[10]，见式(2)。根据对断面1,断面2的现场监测沉降数据反算后，得到该工程的地层损失率约为0.57%，将作为关键参数输入数值模型分析下穿施工影响。

(1)

(2)

其中，x，S(x)，Smax，i和r分别为距离隧道水平距离、沉降、地表最大沉降量、宽度系数和隧道半径。

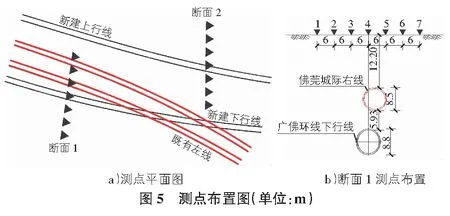
由于广佛环形下行线(既有左线)埋深较大，且两线隧道相距较短，所以盾构施工时，左线隧道的变形相较于右线隧道要更大，因此本文主要研究左线隧道的变形沉降规律。

3.1 数值模拟分析

3.1.1 既有隧道沉降

如图 7为沉降特性曲线，随着盾构开挖的进行，既有隧道不同部位处的沉降曲线规律总体为略微上升—急剧下降—趋于稳定。开挖面距离两隧道交叉点4D时，可以发现既有隧道的沉降值有所增大，有轻微的隆起的现象； 随着开挖面向隧道交叉点靠近，左拱腰部位首先开始出现沉降，这是因为既有隧道左拱腰部位最先进入盾构扰动区域，且沉降速率随着盾构开挖的进行而不断增大，拱顶、拱底和右拱腰亦有类似规律。当开挖面与交叉点距离为-1D，0D，1D，2D时，既有隧道拱底的累计沉降占比分别为1.1%，42.6%，82.9%，90.4%。此外，在整个盾构开挖过程中，拱底和拱顶沉降量最终稳定值分别为7.24 mm和5.3 mm。

图8为既有隧道拱顶、拱底、两侧拱腰四个典型部位随盾构开挖过程中的水平位移曲线(以盾构掘进方向为正)。从图中可以看到，既有隧道各部位的变形方向均与盾构掘进方向一致，但既有隧道不同部位的水平位移发展趋势有所不同，最终水平位移量也互不相同：开挖面距离两隧道交叉点4D时，既有隧道整体水平位移开始逐渐增大，方向为中部向前；随着盾构推进，在(-4D，-1D)区域时，拱顶及拱底两处部位水平位移值平稳增长，而左右拱腰在开挖面经过既有隧道正下方时，水平位移值有所下降，右拱腰处降低的位移值大小要大于左拱腰；在开挖面与两隧道交叉点重合后，拱腰位移方向又转变为朝盾构方向移动；当开挖面与交叉点距离大于两倍隧道直径(2D)后，隧道水平位移值大小趋于稳定。总体来说既有隧道在下穿施工过程中水平位移的发展过程为“向前—稍向后回归—再向前”。

盾构推进过程中，拱顶和拱底的水平位移差异反映出隧道发生了扭转。如图所示，差异值在开挖面经过(-4D，-1D)区间逐渐增加至0.54 mm，在(-1D，0)区间减少到0.37 mm，经过(0,1D)区间差异值继续增加到0.75 mm，随即差异值再次减少，最后稳定在0.3 mm左右。说明既有隧道在盾构下穿过程中经历了向前扭转—稍向后扭转—再向前扭转—回转的复杂过程。

3.1.2 地层应力传播

地层应力发生改变是导致地层变形的主要原因，图 9a)为既有隧道纵向土压力分布曲线图。从图9中可以看到，既有隧道拱顶土压力以新建隧道中线为界近似对称，在中线位置处变化较大。纵向土压力分布曲线整体呈现出以新建隧道轴线为中心，中间低两侧高的“V”形，可见施工扰动在地层的传播和发展会受到既有隧道的影响。离新建隧道轴线中心线距离越近，夹层土竖向土压力越小，最小土压力值出现在新建隧道轴线上方，最大土压力在水平方向上距新建隧道约1D处，明显大于相同埋深的原始土压力。

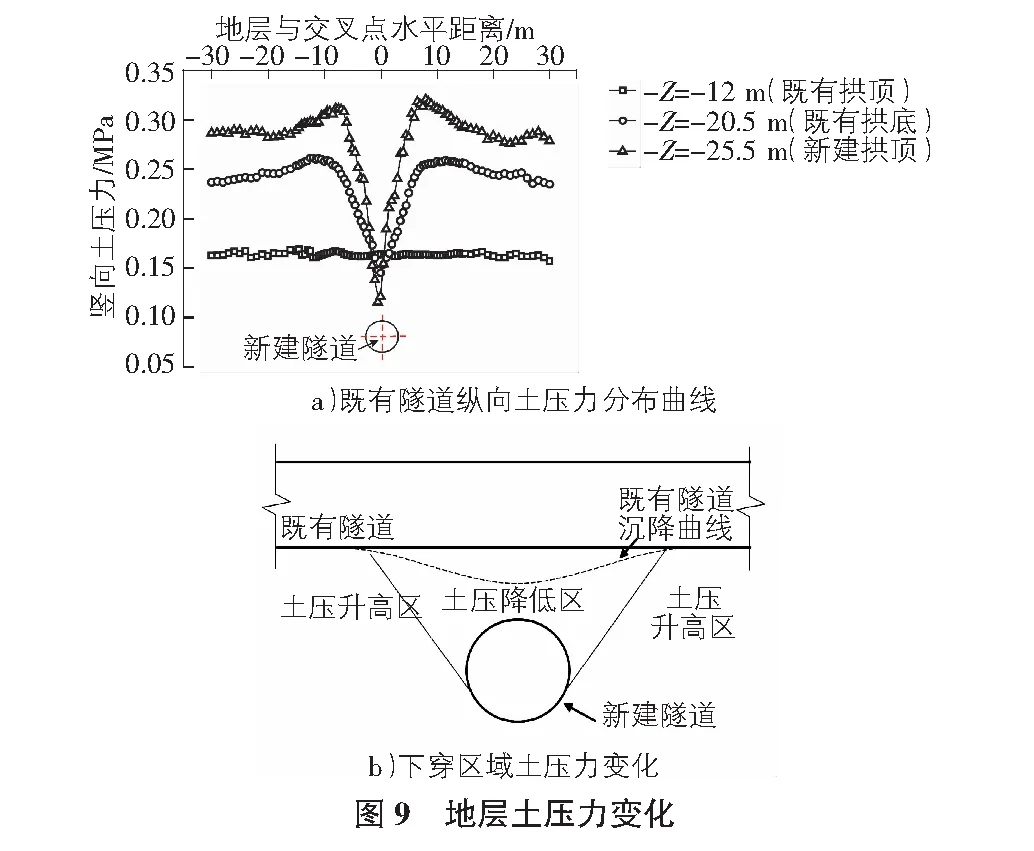
总的来说，既有隧道下方土体应力降低使其隧道受到附加应力是引起既有隧道沉降变形的直接原因。新建隧道盾构掘进时，新建隧道与既有隧道之间的夹层土受到扰动，向新建隧道内塌落，拱顶处的土层塌落后会继续向周围蔓延，由于破坏了原有地层的平衡状态，所以在新建隧道左右拱腰上侧会形成松动圈，周围土体强度下降。当夹层土土层条件较好，厚度较大时，松动圈在扩张过程中会形成稳定的承载拱，承载拱的存在可以起到约束松动圈土体的作用，限制松动圈面积进一步扩大，同时可以类似拱一样“拖”起隧道上方部分土体，分担上部荷载，提高隧道承载力。当土层厚度较薄强度较低时，只会出现松动圈而难以形成承载拱。由于缺少承载拱的约束，盾构机开挖对周围土体扰动形成的松动圈会继续向既有隧道方向延展，当松动圈发展到一定程度后，最终使既有隧道拱底与土层脱离。

3.1.3 既有隧道纵向应力

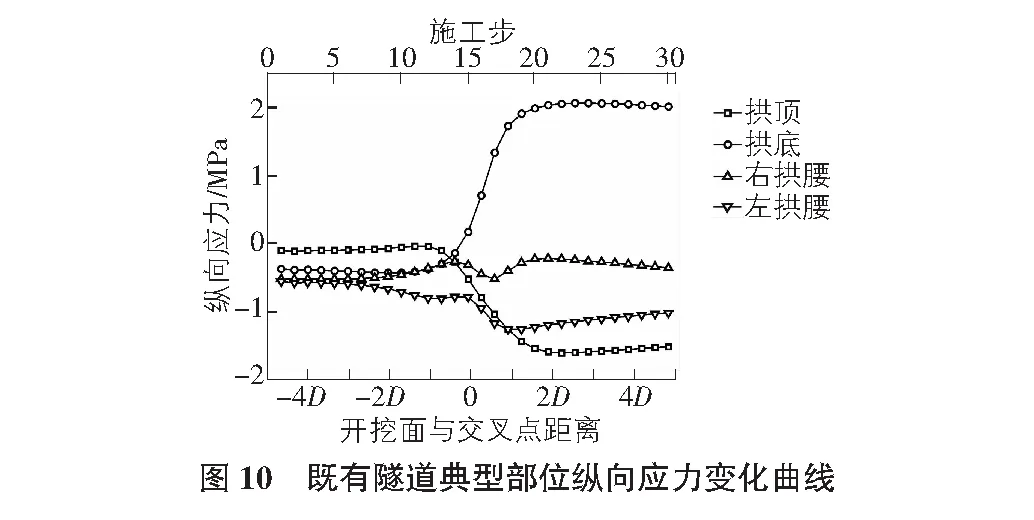
如图 10所示，既有隧道交叉截面不同部位的受扰范围和变化趋势有很明显的不同。左右拱腰受扰范围在开挖面经过(-2D，1D)区段，变动幅度较小；拱底和拱顶受扰范围在(-1D，1D)区段，拱顶压应力急剧增加为截面最大压应力，拱底由较小的压应力迅速增长为拉应力，而隧道的纵向抗拉强度低，这对既有隧道衬砌的安全十分不利，可能引起衬砌拉裂，影响隧道正常使用，需在施工时重点监测下穿段纵向应力变化。

3.2 下穿工程参数敏感性分析

为掌握盾构隧道下穿施工对既有隧道的影响规律，使用有限元软件MIDAS模拟不同工况盾构下穿施工过程，探究地层弹性模量、覆土厚度、隧道净距、隧道下穿角度以及地层损失率等因素对既有隧道变形沉降的影响。

通过合理简化模型，可以保证计算准确的同时提高计算效率，有限元计算模型不考虑土体的不均匀性，采用单一均质地层，服从Drucker-Prager弹塑性屈服准则。地层参数基于珠三角地区常见的地层参数取值(γ=19 kN/m3，E=40 MPa，v=0.3，c=26 kPa,φ=23°)，对应位置关系为(C=12 m，P=4 m，θ=45°，D=6 m，地层损失率为1%)。

3.2.1 弹性模量E的影响分析

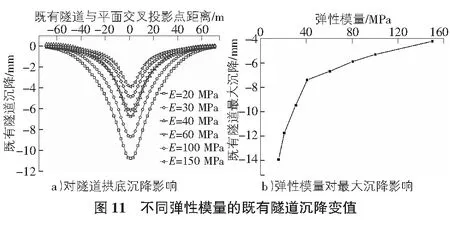
通过改变地层的弹性模量，得到不同地层弹性模量下的既有隧道沉降值，计算结果如图11 a)所示。从图中可以看到，随着围岩弹性模量降低，既有隧道最大沉降值及隧道周围土体扰动范围均会明显增加。当围岩弹性模量较小时变形相对较小。

如图11 b)所示，以弹性模量40 MPa为分界点，当弹性模量小于40 MPa时，沉降最大值随弹性模量变化幅度较大；而大于40 MPa时规律则相反。

总体而言，隧道的沉降峰值随着围岩的弹性模量的增大而减小，围岩弹性模量对既有隧道的变形影响较大。

3.2.2 覆土厚度C的影响分析

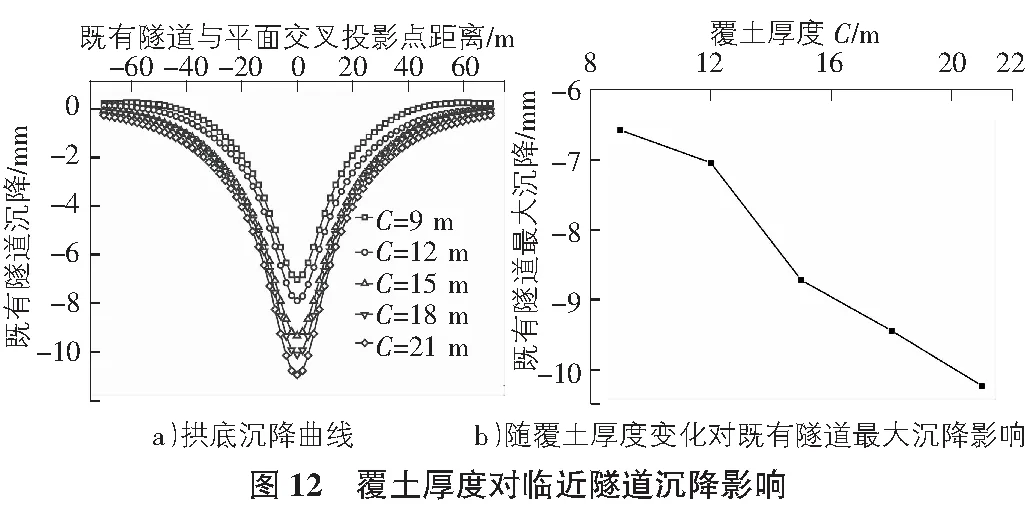
改变覆土厚度后，可以看到既有隧道的沉降曲线均有差异(见图12)，可见覆土厚度对既有隧道的整体沉降影响较大。随着覆土厚度的增加，既有隧道的沉降值也在不断扩大。这是因为隧道埋深增大后，新建隧道周围地层土压力也相应增大，盾构施工后地层应力重分布作用更明显。

3.2.3 新旧隧道净距P的影响分析

当新旧隧道净距大于1D时，随着两线隧道净距的增大，沉降槽的形状也逐渐改变。随着既有隧道周围土体扰动区域的逐渐增大，沉降槽宽度相应增加，整体形状由窄变宽，从 “漏斗状”变成 “盆状”(见图 13)。

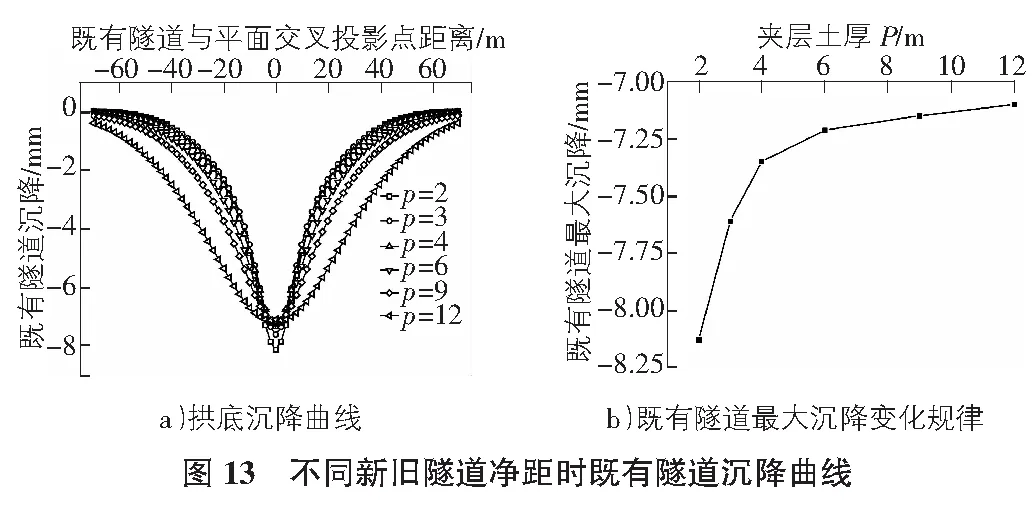
既有隧道最大沉降值随两线隧道净距的降低而逐渐增大，当两线隧道之间的夹层土厚度小于1D时，新旧隧道净距对沉降峰值影响很大；当夹层土厚度大于1D后，对既有隧道沉降影响减小。因此，为了减小既有隧道的沉降峰值，降低施工风险，在设计下穿隧道线路时应保证新旧隧道之间留有一定的净距。

3.2.4 下穿角度θ的影响分析

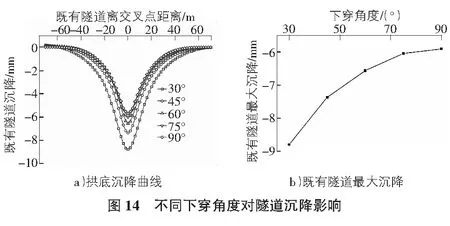
下穿角度对既有隧道沉降峰值影响见图14。交叉角度每隔15°从30°增至75°的过程中，既有隧道沉降分别减少了19.4%，11.0%，7%；从75°增至90°时，既有隧道沉降趋于稳定，基本无变化。因此，在设计阶段适当增大隧道下穿角度可以降低既有隧道的沉降峰值。

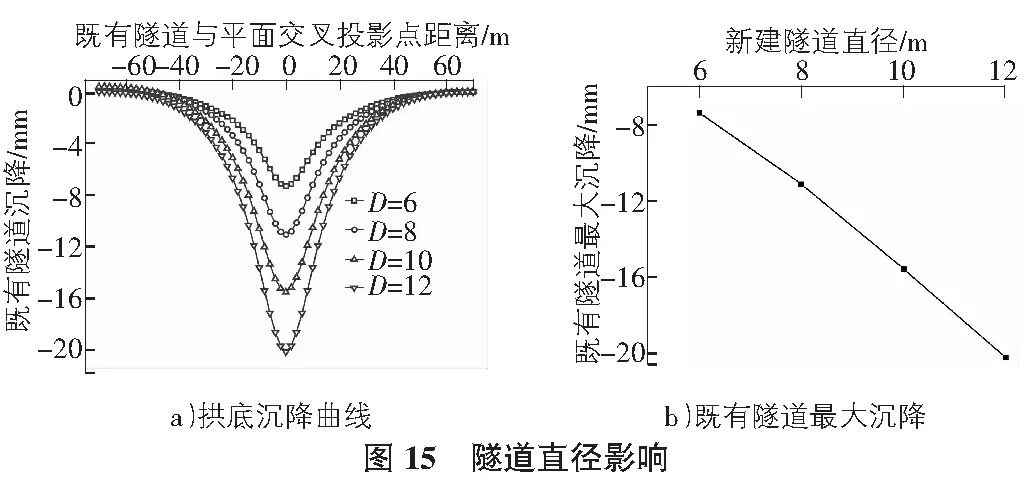
3.2.5 新建隧道直径D的影响分析

从图15可以看出，既有隧道沉降峰值随盾构直径增加而不断增大，且增长非常迅速。盾构直径对既有隧道变形有较大影响有两个原因：一方面是因为增大隧道直径后，在相同覆土厚度且新旧隧道净距保持不变时，隧道的埋深也相对增加，此时隧道周围土压力也随之增大，盾构掘进扰动原有土层后，土体再次恢复平衡状态所需时间更长；另一方面，假设工程所处区域地层损失率保持不变，由于隧道直径增大，实际开挖土体体积与建成的隧道体积之差会成倍增长。因此在进行大直径隧道施工时，如果要增大隧道直径，必须控制好地层损失体积量，减小隧道沉降值。

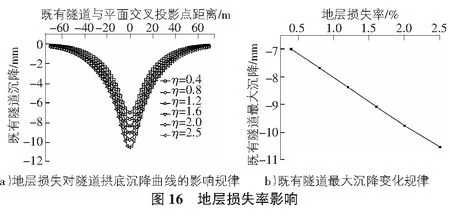
3.2.6 地层损失的影响

如图16所示，既有隧道沉降最大值与地层损失率近似呈正相关。平均地层损失率每增加0.25%，既有隧道沉降峰值约增加0.42 mm。

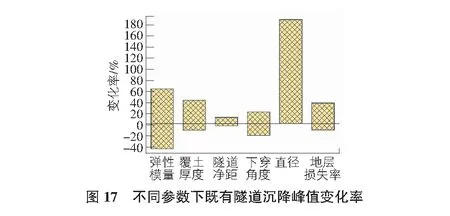
3.2.7 参数敏感性分析

盾构隧道的直径变化对既有隧道沉降峰值影响最大，其他因素(地层弹性模量、覆土厚度、下穿角度、地层损失率)对既有隧道沉降的影响相当(见图17)。因此既有隧道的变形控制可对土体进行注浆加固处理，增加隧道周围的土体的强度。

4 结论

本文利用数值仿真对盾构下穿既有隧道的变形特性展开系统研究，主要得到了以下结论：

1)既有隧道变形是新建隧道施工后隧道上半周土体形成松动圈，土压力降低所致。

2)当盾构开挖面经过交叉点前后各1D区间时，下穿施工对既有隧道的影响最大。既有隧道在该区间的沉降接近整个既有隧道总沉降的80%。既有隧道远离扰动区域后，最大沉降出现在两隧道平面交叉位置衬砌拱底处，为7.24 mm。

3)盾构隧道的直径变化对既有隧道沉降峰值影响最大，其次是地层弹性模量，其他影响因素(覆土厚度、新建隧道下穿角度、地层损失率)对既有隧道变形特性的影响程度相当。综上所述，实际工程中要控制既有隧道的变形量可对土体进行注浆加固处理，增加隧道周围的土体强度。