降雨作用下南水北调膨胀土渠道稳定性及影响因素

沈丹萍，何 军，任 杰，王 媛

(1. 河海大学力学与材料学院，南京 211100； 2. 南水北调中线干线工程建设管理局，北京 100038； 3. 河海大学水利水电学院，南京 210098)

南水北调工程是为缓解中国水资源分布不均、优化水资源配置而兴建的大型调水工程，包括东、中、西三条线路。其中中线工程全长1267km，横跨四省，经过分布有膨胀土(岩)地区的长度达到387km。降雨诱发边坡失稳的原因：一方面增加土体的重度，使边坡滑动面上的下滑力加大；另一方面提高土体含水率，使孔隙水压力升高，基质吸力减小，有效应力降低，从而降低滑动面上的抗剪强度[1-5]。膨胀土具有胀缩特性[6-8]，对土体含水率的变化十分敏感，天然状态下含水率较低，边坡强度很高，降雨作用下土体吸水膨胀，含水率升高，边坡强度大大降低，所以深入研究降雨作用下膨胀土渠道边坡的稳定性，对于南水北调工程的治理和防护具有指导性意义。

降雨作用改变了土体的润湿特性，降低了边坡的安全系数。王俊光等[9]考虑降雨强度和降雨历时对边坡稳定性的影响，发现边坡安全系数随降雨强度和历时的增加而明显减小；汪勇等[10]通过试验和数值模拟相结合，发现降雨过程中，土体含水率的变化对抗剪强度参数的影响显著，尤其是黏聚力；王一兆等[11]基于非饱和渗流理论发现，边坡浅层滑动面安全系数在降雨期连续减小，停雨后均增大；王述红等[12]基于ABAQUS耦合渗流场和应力场分析降雨对边坡稳定性的影响，发现对比降雨时长，浅层土体形成饱和区的速度和降雨强度相关性更大，极易发生浅层滑坡；聂超等[13]以西南某机场某高填方边坡为例，通过数值模拟并结合实际勘查报告，分析了不同降雨强度、降雨时长等条件下边坡的变形情况；韩廷文等[14]以露天矿高填方为例，基于Geostudio软件模拟了边坡的安全系数及表面水平位移随降雨强度和降雨时长的变化规律。上述研究大都是分别从含水率、安全系数、位移中的一个或两个指标出发来分析降雨条件下的边坡稳定性，较少综合考虑多个指标，对边坡稳定性进行整体、系统化地研究；同时上述研究只考虑了降雨强度、降雨时长对稳定性的影响，然而降雨过程中，影响边坡稳定性的因素较多，且影响程度各不相同，因此有必要对边坡失稳的影响因素进行敏感性分析，确定各因素的主次关系，为边坡的稳定性评价提供依据。

关于边坡稳定性影响因素敏感性分析方面，传统的分析方法如主成分分析、方差分析、回归分析等，不仅需要大量的计算，而且对样本数据的要求很高，在实践中有很大的局限性[15]；正交试验法可以减少试验次数，减小计算量，但无法考虑各因素之间互相影响的情况[16]。基于正交实验结果进行灰色关联分析不仅可以克服传统方法的缺点，同时可以考虑多个因素的相互影响效应。

在上述研究基础上，现以南水北调膨胀土渠道某高填方断面为例，对比分析考虑和不考虑非饱和渗流对边坡稳定性的影响，验证考虑非饱和渗流的必要性，然后基于饱和-非饱和渗流理论，分析降雨作用下膨胀土渠道边坡内部的含水率、孔隙水压力、安全系数和位移的变化规律，并结合正交试验和灰色关联理论对影响边坡稳定性的因素进行定量分析，确定最不利因素，为南水北调工程降雨条件下渠坡的防护提供依据。

1 非饱和渗流理论和灰色关联理论

1.1 渗流微分方程

用于二维非饱和渗流计算的控制方程为

(1)

式(1)中：H为总水头，m；kx、ky分别为x和y方向的渗透系数，m/s；Q为施加的边界流量，s-1；mw为土水特征曲线的斜率，kPa-1；rw为水的容重，kN/m。

上述渗流方程求解的前提是确定模型的初始条件和边界条件[17]，即

H(x，y，t)|t=0=H0(x，y，t0)

(2)

H(x，y，t)=f(x，y，t)|(x，y)∈Γ1

(3)

q(x，y，t)|(x，y)∈Γ2

(4)

式中：H0(x，y，t0)为初始时的水头分布；Γ1为水头边界，m；Γ2为流量边界，m/s；f(x，y，t)为水头分布函数；q(x，y，t)为单位时间内的法向流量函数(入渗为正，逸出为负)； cos(n，x)、 cos(n，y)为边界面沿外法线方向的余弦值。

1.2 非饱和土的抗剪强度

使用Fredlund等[18]提出的可以分别考虑总法向应力和孔隙水压力变化的影响的抗剪强度公式预测非饱和土的抗剪强度，即

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(5)

式(5)中：c′为有效黏聚力，kPa；φ′为有效内摩擦角，(°)；φb为吸力内摩擦角，(°)； (σ-ua)为净法向应力，kPa； (ua-uw)为基质吸力，kPa。

采用Vanapalli等[19]提出的可以替换φb的公式，即

(6)

式(6)中：θw为体积含水率；θr为饱和体积含水率；θs为残余体积含水率。

1.3 灰色关联分析法基础理论

灰色关联分析法的理论基础是选取影响因素自变量作为子序列，系统特征因变量作为母序列，通过对比分析子母序列数据曲线之间的几何接近程度来计算各个影响因素的关联度，进而评价其影响的主次程度。计算步骤如下。

(1)定义子母序列矩阵。设子序列矩阵为X，母序列矩阵为Y。

(7)

(8)

式中：n为自变量个数；m为因变量个数。

(2)对X、Y矩阵进行无量纲处理。为了消除矩阵中数据的单位和量级不同的影响，采用区间相对值的方法对矩阵X、Y进行处理，得到矩阵X′和Y′中的各元素表示如下。

(9)

(10)

式中：xij为第j个影响因素相应第i个水平值；yij为xij对应的安全系数的均值。

(3)计算关联系数矩阵和关联度。由式(11)计算X′和Y′矩阵中对应数据的绝对差值得到差异矩阵为

Δij=|x′ij-y′ij|

(11)

取Δij中的最大值和最小值为

Δmax=maxΔij

(12)

Δmin=minΔij

(13)

关联系数矩阵中的各元素表示为

(14)

式(14)中：η为分辨系数，取值区间为[0，1]，一般取η=0.5。

(4)计算关联度。由关联系数矩阵按照式(15)计算得各影响因素的关联度为

(15)

式(15)中：rij为关联系数矩阵的各元素；k为各影响因素所取水平数，g∈[0，1]，g越接近1，表示影响因素对系统因变量的影响程度越大，反之越小。

2 有限元计算模型

首先对比分析了考虑和不考虑非饱和渗流对边坡稳定性的影响，然后基于SEEP/W计算得到的饱和-非饱和渗流场，分析降雨因素对含水率和孔隙水压力的影响，最后考虑不同降雨因素下的孔隙水压力分布规律，分析不同降雨因素下渠道边坡的安全系数和位移的变化规律。

2.1 计算模型及参数

以南水北调某高填方渠段为例，选取研究断面如图 1所示，该截面渠堤填高12m，堤顶宽度为5m，渠堤内外坡比1︰2，距堤顶6m设置一级马道，马道宽度2m。

用于数值模拟的膨胀土边坡网格如图2所示，其中A为监测点。考虑到渠道表面铺有水泥改性土、土工膜和混凝土面板，因此在模型上游面设置一层渗透系数很小的单元(区域2)，区域1为渠道堤身填土。

采用Van Genuchten模型描述膨胀土的土水特征曲线，如图 3所示，饱和体积含水率为0.49%，残余含水率为0.1%。

图 1 高填方断面示意图Fig.1 Schematic diagram of high fill section

图 2 有限元模型Fig.2 Finite element model

图 3 土水特征曲线Fig.3 Soil-water characteristic curve

根据该高填方段监测资料显示，堤顶已出现裂缝，故对表层土的渗透系数进行优化，取饱和渗透系数为4×10-5m/s。渗透系数与基质吸力的关系如图 4所示。

图 4 渗透系数与吸力的关系Fig.4 Relationship between permeability coefficient and matric suction

图 5 渗流模型中边界条件Fig.5 Boundary conditions in the seepage model

2.2 模型边界及初始条件

模型施加的边界条件如图 5所示。

其中： 上游面考虑到渠道水位，设置为总水头边界；从堤顶到一级马道处铺设有土工膜，设为不透水边界；堤顶、一级马道至坡底在初始状态设为自然边界，降雨时设为流量边界；模型底部设为不透水边界。

渠道的设计水深为7m，模型在初始状态的孔隙水压力分布仅考虑上游渠道水位的影响，因此以考虑上游水位7m时SEEP/W计算的稳态渗流场作为模型的初始条件。

2.3 降雨工况设计

根据现有监测资料，该断面所在叶县段的年降雨量如图 6所示，实测最大日降雨量为90.6mm，实测年总降雨量为612.6mm。

图 6 叶县管理处辖区2018年降雨量变化过程线Fig.6 Rainfall change process line in the jurisdiction of Ye County Management Office in 2018

根据该地年降雨量变化，选取3种工况，考虑大、中和小降雨强度，如表 1所示。

表 1 降雨工况Table1 Rainfall conditions

3 数值模拟结果

3.1 考虑非饱和渗流对边坡稳定性的影响

以同一渠道断面为研究对象，分别在考虑非饱和渗流和不考虑两种情况下，基于有限元方法，计算得到不同强度参数下边坡的安全系数如表 2、表3所示。

表 2 不考虑非饱和渗流下边坡的安全系数Table2 Safety factor of slope without considering unsaturated seepage

表 3 考虑非饱和渗流下边坡的安全系数Table3 Safety factor of slope considering unsaturated seepage

从表 2、表3可以发现，考虑非饱和渗流时，在不同强度参数下计算得到的边坡安全系数相比于不考虑时均降低。该断面在2016年4月7日发现裂纹，根据监测数据显示，2018年10月14日位移发生突增，初步假定为发生滑移。对该断面进行有限元分析，考虑非饱和渗流时计算得到的渠道边坡安全系数为1.18，非常接近1.0，即渠道发生滑坡的概率很大；但是不考虑非饱和渗流时计算得到的渠道边坡的安全系数为1.37，即渠道处于较安全的状态。由此可见，考虑非饱和渗流下边坡稳定性分析结果更能反映渠道真实的运行状态。

3.2 降雨因素对边坡渗流场的影响

按照表 1计算得到的边坡孔隙水压力分布如图7(a)～图7(f)所示。

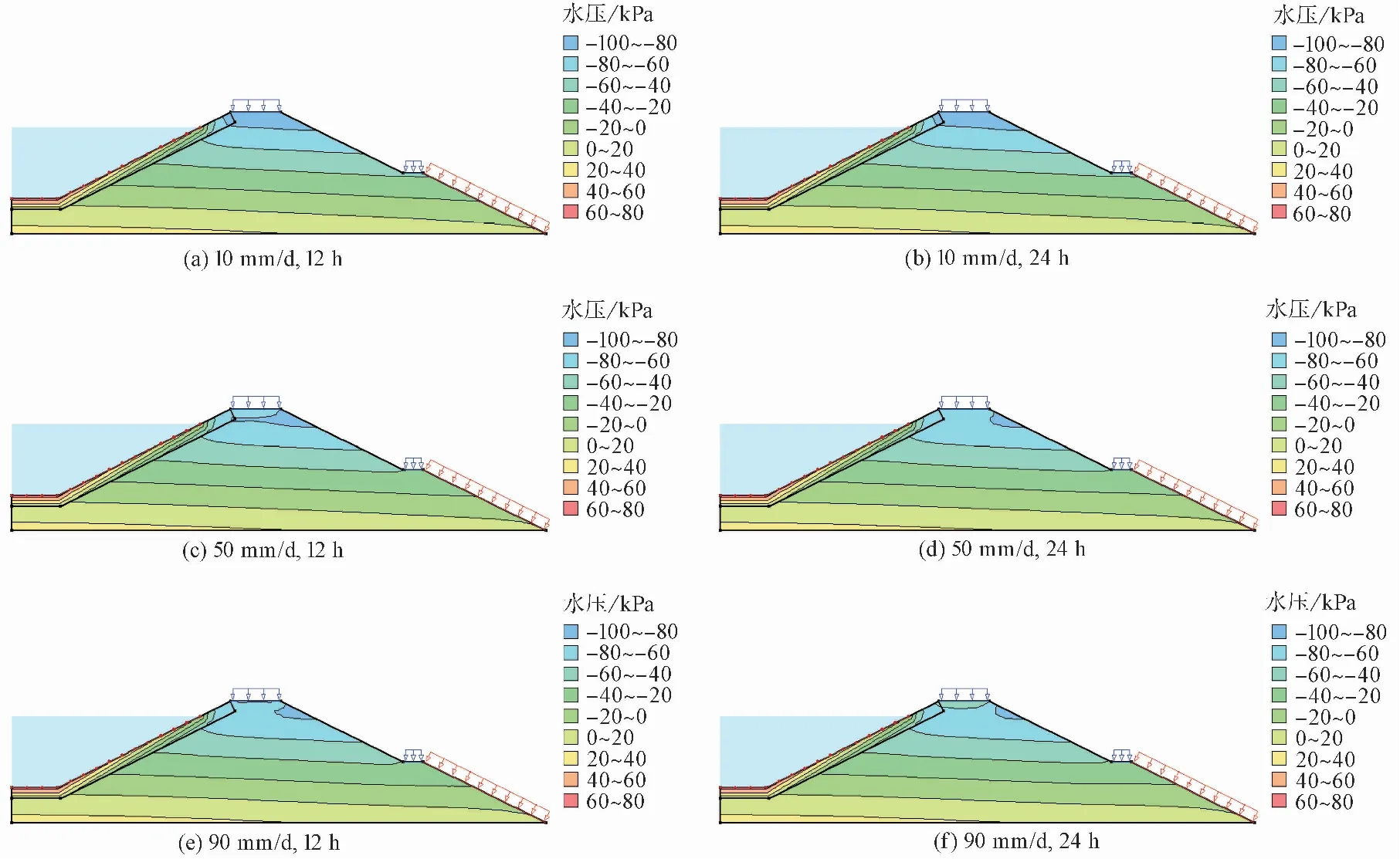
图 7 边坡孔隙水压力分布Fig.7 Distribution of pore water pressure in slope

分析图 7 发现，随着降雨入渗，边坡的孔隙水压力开始增大，最小孔隙水压力-100～-80kPa的土体范围逐渐减小；当降雨强度增加到50mm/d时，边坡浅层土体的孔隙水压力增加到-80～-60kPa，并且随着降雨时长的增加，这一土体范围快速增大；到降雨强度增加到90mm/d时，边坡浅层土体的孔隙水压力已达到-60～-40kPa。

为分析降雨因素对渠坡土体含水率的影响，取降雨强度为10、50、90mm/d，降雨时长为8、16、24h共9组工况，分别以堤顶和一级马道右侧的纵剖面为研究对象，其含水率沿埋深方向的分布如图 8所示。

分析图8发现，降雨对边坡浅层土体的含水率的影响较大，深层土体的含水率在整个降雨过程中几乎不变化，从堤顶往下，受降雨影响的土体深度范围在0～2.5m；从一级马道往下，受降雨影响的土体深度范围在0～5m，其中0～1.5m范围内的土体受影响的程度较大。对比分析含水率受影响的程度：降雨强度90mm/d、时长8h>降雨强度50mm/d、时长16h；降雨强度50mm/d、时长8h>降雨强度10mm/d、时长24h；即短时强降雨下，边坡浅层含水率变化幅度更明显，表明降雨强度对渠坡浅层土体的影响程度更大。

3.3 降雨因素对渠坡位移变化规律的影响

由于渠道水位和自重作用，边坡在降雨前就存在沿X和Y方向上的位移，如图 9(a)和图9(b)所示。在X方向，边坡上游土体受渠道水位的影响出现向右(下游)的位移；在Y方向，边坡土体主要是向下的沉降位移，并且堤顶的沉降值最大，底部最小。

图 8 堤顶和一级马道右侧纵剖面含水率分布Fig.8 Water ratio curves in longitudinal section on the right side of the top embankment and the first stage

图 9 降雨前边坡位移Fig.10 Slope displacement before rainfall

图 10 降雨后边坡位移Fig.10 Slope displacement after rainfall

图10(a) 和图10(b)分别是降雨强度为90mm/d、历时1d后边坡沿X和Y方向的位移云图。对比图 9(a)和图10(a)发现，降雨作用下边坡浅层土体的含水率变化最明显，土体吸水膨胀导致位移出现轻微的回弹，上游浅层土体有向左的位移，下游浅层土体有向右的位移；对比图 9(b)和图10(b)发现，由于浅层土体在降雨作用下吸水膨胀，Y方向的沉降位移也出现减小趋势。

选取图 2中堤顶右(A)端点作为监测点，其位移在不同降雨强度下随降雨时长的变化如图 11所示。

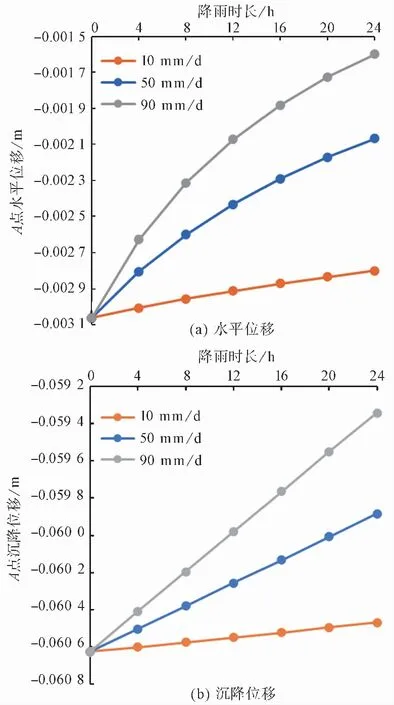
图 11 降雨过程中A点水平位移、沉降位移变化曲线Fig.11 Horizontal and settlement displacement curve of point A during rainfall

从图11(a)和图11(b)中可以看出，在同一降雨强度下，随着降雨时长的增加，监测点A的水平位移和沉降位移都逐渐减小；在同一降雨时长下，降雨强度越大，位移减小的幅度越大。

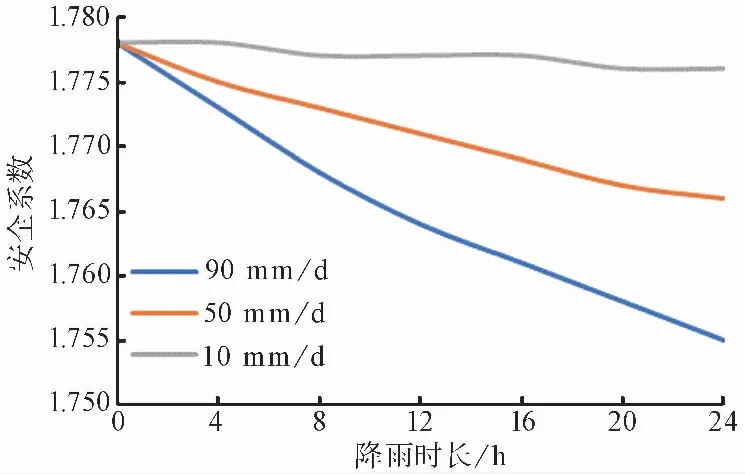
图 12 不同降雨强度下边坡安全系数随降雨时长的变化曲线Fig.12 Variation curve of slope safety factor with rainfall duration under the different rainfall intensity

3.4 降雨因素对渠坡稳定性变化规律的影响

在3种工况下，将SEEP/W计算的不同时刻的瞬态孔隙水压力分布导入到SLOPE/W中分析边坡稳定性变化规律。采用Bishop法计算安全系数，如图 12 所示。

由图12可知，在同一降雨强度下，边坡安全系数随着降雨时长的增加而降低；在同一降雨时长下，降雨强度越大，边坡安全系数降低的幅度越大。

3.5 影响渠坡稳定性因素的敏感性分析

选取影响边坡稳定性的6个主要因素：降雨强度(X1)、降雨历时(X2)、黏聚力(X3)、内摩擦角(X4)、饱和渗透系数(X5)和重度(X6)，设计6因素5水平的正交试验，然后基于灰色关联理论对正交试验结果耦合分析，最后对各个影响因素的敏感性进行评价。

3.5.1 正交试验

不考虑上述6个影响因素间的交互作用，每个因素取5个水平，设计6因素5水平的正交试验，各个因素及对应水平的取值以及正交试验结果如表 4、 表5所示。

表 4 影响因素水平Table4 Levels of influencing factors

表 5 正交试验结果Table5 Results of orthogonal experiment

3.5.2 灰色关联耦合分析

选取正交试验中6个影响因素对应的各水平值作为子序列矩阵X，各水平对应安全系数的均值作为母序列矩阵Y。

(16)

(17)

由式(9)、式(10)对X、Y矩阵进行无量纲处理，然后由式(11)计算的差异矩阵Δij为

(18)

由式(10)～式(12)计算得到关联系数矩阵R为

(19)

最后由式(13)计算得到关联度矩阵D为

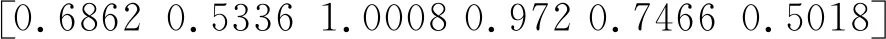
(20)

上述计算结果表明，影响边坡稳定性因素的敏感性排序：黏聚力>内摩擦角>饱和渗透系数>降雨强度>降雨时长>土体重度；在降雨过程中，土体的强度参数对边坡稳定性的影响最明显，重度则相对较小。

4 结论

研究非饱和渗流对边坡稳定性的影响，基于饱和-非饱和渗流理论分析降雨作用下南水北调高填方渠道边坡的渗流场、位移和稳定性变化规律，并结合正交试验和灰色关联理论对影响边坡稳定性的因素进行敏感性分析，得出如下结论。

(1)考虑非饱和渗流下边坡稳定性分析结果更能反映渠道边坡真实工作状态。

(2)降雨过程中，边坡浅层一定深度内土体的孔隙水压力迅速增大，并随着降雨强度增大和时长增加，这一土体范围向深部扩展；降雨对堤顶向下0～2.5m范围和一级马道向下 0～5m范围内土体含水率的影响较大，深层土体的含水率在整个降雨过程中几乎不变化，土体含水率同时受降雨强度和时长的影响，但降雨强度的影响更显著，因此在渠道防护时，应密切关注浅层土体含水率在降雨过程中的变化。

(3)降雨过程中，渠坡浅层土体含水率迅速增大，土体吸水膨胀导致位移出现轻微的回弹；随着降雨时长的增加，浅层土体的水平位移和沉降位移逐渐减小，并且降雨强度越大，位移减小的幅度越大。降雨过程中，渠坡的安全系数逐渐降低，并且降雨强度越大，降幅越大。

(4)影响边坡稳定性因素的敏感性排序：黏聚力>内摩擦角>饱和渗透系数>降雨强度>降雨时长>土体重度；在降雨过程中，土体的强度参数对边坡稳定性的影响最明显，重度则相对较小，降雨强度的影响程度大于降雨时长。