基于多源数据分析的变电站状态维护策略优化方法

钱宇骋，朱太云，甄 超，赵常威

(1. 国网安徽省电力有限公司电力科学研究院，合肥 230601； 2. 国网安徽省电力有限公司，合肥 230001)

电力行业的发展离不开电力系统的发展，电力系统由众多部件组成，如电力变压器、断路器和输电线等。随着系统不断的运行，部件可能出现故障及缺陷，这将严重影响电网维护运行中的稳定性并将带来不可预测的经济损失。此外，随着中国电力行业的发展，电力系统数据急剧增加，当前已达到千万亿字节(petabyte，PB)水平。这意味着当前电力行业正进入大数据时代[1-4]。因此基于海量数据研发可稳定保障电网运行的维护策略势在必行。

变电站状态的维护是供电保证与电力安全的基础工作，但通常情况下都具有较大的不确定性以及不可控性[5-7]，因此对变电站的维护提出了更高的要求。当前应用于变电站电网维护已有不同的策略，如基于时间的维护策略，纠正性维护策略及基于状态的维护(condition based maintenance，CBM)策略。与前两者相比，CBM因其能减少故障损失及延长设备使用寿命从而得到了广泛的应用[8-10]。文献[11]提出了一种能够同时兼顾变电站供电可靠性和设备全寿命周期成本的设备检修决策优化方法。文献[12]提出了一种基于役龄回退分析的弹性周期和状态的检修决策优化算法，该算法可以预测检修后的故障率。文献[13]提出了一种基于检修风险收益的输变电设备检修优先级排序方法，以解决在检修资源有限情况下设备检修优先级的排序问题。然而上述文献存在较为明显的缺点。首先用于决策的样本信息较少，一些关键的参数和因素的值往往被经验值取代，其次维护对象往往是单一组件，在电力系统中不同组件之间的连接可能导致区域性的故障，对区域内所有设备进行维护能减少中断时间。

针对上述问题，现提出一种基于多源数据分析的变电站状态的CBM策略优化方法。首先，分析可用于变电站维护的状态数据；其次，提出系统维护单元的概念，结合不同组件之间的互连关系，将变电站分为不同的维护单元进而对不同的维护单元中组件进行统一维护；再次，为定量评估维护前后零件的可靠性，分别建立基于健康指数(health index，HI)和寿命降低因子的失效率计算模型。为获得良好的经济效益，建立基于生命周期成本理论(life cycle cost，LCC)理论的CBM优化模型。最后，通过案例验证所提策略的有效性。

1 CBM维护数据1.1 数据管理系统

为了更好地处理电力系统中日益增长的数据，已经开发了许多数据管理系统，如信息管理系统(management information system，MIS)、能源管理系统(energy management system，EMS)、生产管理系统(production management system，PMS)等。每个系统为不同的应用程序存储不同类型的数据。因此，寻找和获取这些数据对优化维护策略具有重要意义。根据一些标准和参考文献[14-16]，现简要介绍一些重要的数据管理系统。

(1)MIS。它存储每个组件的基本信息。例如铭牌数据，包括名称、生产厂家、额定电流和额定电压、运行时间、负载损耗和空载损耗等。铭牌数据将直接影响CBM，此外，铭牌数据也是确定组件故障时间和维护方式的关键影响因素之一。

(2)EMS。EMS的数据反映了设备和变电站的负荷水平，这对CBM调度有较大影响。EMS数据包括有功功率、无功功率、电流和电压。

(3)PMS。PMS用于记录电力设备的管理信息，包括设备帐户信息、故障或缺陷的历史记录、检查和预防性测试数据等。一些潜在的故障，以及异常组件的位置和严重程度，都可以通过PMS数据找到。

1.2 其他类型数据

除了上面提到的系统，对维护策略的优化过程还应该参考其他类型的数据。

(1)LCC。LCC定义为购买、使用、维护和报废组件的所有成本[14]。维护策略对LCC的影响很大，尤其是部件的维护成本和故障成本。LCC是评估不同CBM策略经济性的有效经济分析工具，它被用作许多CBM策略优化模型的最优目标。

(2)变电站的电气主接线图。在变电站中，不同类型的组件相互连接。组件的运行或中断状态受其自身或其他组件影响。例如，在电力系统中，某个组件故障可能导致其他组件故障[10]。因此，可以将这些维护组件安排在一起，以减少平均停运维护时间，并提高变电站的供电可靠性。

(3)状态评估和风险评估。状态评估用于评价电力设备的退化程度和健康水平。风险评估是评估电力系统中组件故障概率的有效工具。预期负荷损失和负荷削减概率是描述电力系统风险水平的常用标准。状态和风险水平是影响CBM调度的重要因素。例如，当多个部件需要维护时，状况较差或风险较高的部件总是要优先维护。

2 系统维护单元及方式

2.1 系统维护单元划分

近年来，为保障电网中输电系统的安全，单偶发性原则(N-1原则)已被广泛的应用。N-1原则要求任何单个组件的故障都不会导致任何负载削减。图 1为具有两个功率流路径的典型变电站配置，每个路径由一个变压器(T1/T2)，4个断路器(DL1、DL2、DL3、DL4)和传输线组成，两条路径互为备用，以满足N-1原则。通常对于单个组件的维护将对变电站的运行产生一定的影响，这将导致变电站的可靠性下降。因此当不同路径的组件需维护时，需要对其进行有序维护，以避免变电站中断。

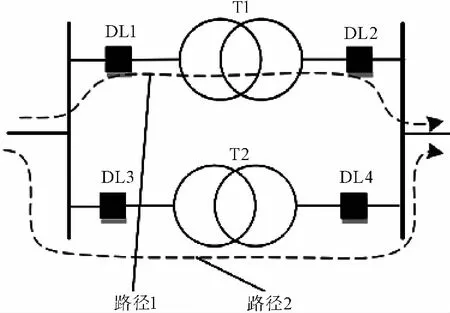
图 1 典型的变电站配置Fig.1 A typical substation configuration

由于变压器、断路器及传输线等不同组件之间的相互连接和相互作用，使得某个组件停止服务并进行维护时将导致其他组件中断。若T1停止运行，则路径1中的电流中断并将导致两个断路器DL1和DL2停止运行。此时在维护时，若对DL1和DL2分次进行维护，将会对某一条路径中断两次，而若对两者同时维护时，中断时间将显著减少。

传统的CBM维护策略的调度目标侧重于不同组件的维护顺序，忽略了组件之间的互联关系，导致难以获得最优结果。为解决这个问题，提出维护单元的概念，将可同时维护的组件(如图 1中T1、DL1和DL2)包含在同一维护单元中，而后将变电站划分为不同的维护单元，并将维护单元视为基本单元从而优化维护策略，如图 1有两个基本维护单元。

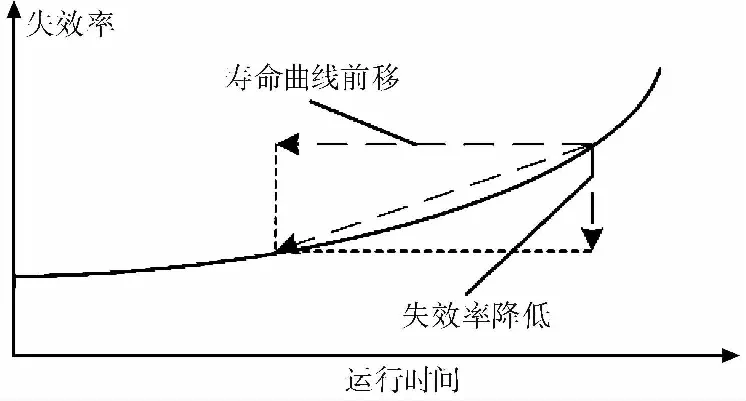
图 2 早期故障期后的失效率Fig.2 Failure rate curve after infant mortality region

2.2 电力设备维护方式

消除组件的不同故障或缺陷需要特定的维护模式。依据文献[12-13]，定义了4种维护模式，分别为A、B、C、D，其中A、B、C为关机维护，D为开机维护。

维护模式A：拆解检修，即对设备进行大修，此情况下维护周期长，维护成本高。

维护模式B：局部检修，对本体以外的部分子组件进行维护或更换，维护费用低于维护模式A。其中，维护B的所有工作包含在维护A内。

维护模式C：小型维护，一般为电力设备的例行监测、维护及调试。其中，维护C的所有工作包含在维护B内。

维护模式D：一般为简单维护，例如变压器的带电清洗，此情况下组件仍可正常运行。

通常情况下，失效率和故障概率被广泛应用于确定所需的维护模式，如模式A用于失效率高的组件，模式B、模式C、模式D用于失效率低的组件，但某些情况下具备一定的局限性，如冷却系统的故障将导致变压器处于高失效率水平，此时无需通过模式A进行维护。

3 失效率

失效率是反映不同维护方式运行状况和维护效果的关键参数。为了定量评估组件维护前后的状态，分别建立了基于HI和寿命降低因子的失效率计算模型。

3.1 基于HI的失效率计算

HI通常用于描述设备的劣化程度。组件的状态可分为正常状态、注意状态、异常状态和严重状态[17]。HI越低，表示组件的状态越差。

基于HI的失效率计算公式为

λ=Ke-ISEC

(1)

式(1)中：λ为失效率；K和C分别为比例参数和曲率参数，可以在采集到HI数据和构件失效数据后通过反演计算得到；ISE为组件健康指数值(该值在0～100)，可通过检测数据和试验数据进行评估。由式(1)可知，设备的ISE越高，意味着失效率λ越低，即组件的状况越好。

3.2 基于寿命降低因子的失效率计算

电力设备在其使用期内的失效率可以用浴盆曲线表示。浴盆曲线表示设备失效率与寿命之间的关系，由3个主要区域组成：早期故障期；正常工作区域；耗损失效期。通常，失效率λ在正常工作区域中保持恒定或缓慢增加，而在耗损失效期会急剧增加。两个区域的失效率可以分别用式(2)和式(3)表示。

λnormal=Const≤T

(2)

(3)

式中：Cons为常量参数；α、β为服从韦伯分布的函数，其中α为比例参数，β为状态参数；t为组件的寿命；T为两个区域之间的截止点。

实际上，很难估计两个区域之间的截止点T。因此综合失效率函数可由式(4)表示，该式中不含参数T，即

表 3 不同维护模式下的η值Table3 The η value of different maintenance mode

表 2 不同模式的停机时间Table2 Outage time of different mode

表 1 维护成本的数据Table1 Data of maintenance cost

(4)

Cons、α和β由分量的λ(t)和t估计，每个分量的λ(t)和t的数据存储在PMS中。在收集了组件数据样本的λ(t)和t之后，利用最小二乘法对这3个参数进行评估。

通过对异常情况组件进行有效的维护操作，可以降低失效率，这类似于寿命曲线在失效率曲线图中前移，如图 2所示。为定量描述不同维护模式之间的失效率变化程度，提出了寿命降低因子η(0<η<1)的概念。维护后的等效寿命teq可通过式(5)计算，公式为

teq=Tactual(1-ηj)

(5)

式(5)中：Tactual通过式(4)的反演计算得到，为维护前的寿命；ηj为维护模式j的寿命降低因子。然后，通过将teq代入式(4)来计算维护后组件的失效率。

4 维护策略优化模型

一般而言，良好的CBM策略通常基于设备和电力系统中不同类型的数据，LCC数据在用于CBM优化模型中可获得经济效益，因此基于LCC理论对CBM策略进行优化。

4.1 电力设备的生命周期成本

电力设备的LCC分为5个部分，分别是投资成本、运行成本、维护成本、故障成本和报废成本。LCC的配置如图 3所示。

图 3 电力设备的LCCFig.3 LCC of power equipment

投资成本包括购买新设备、安装等的成本。运行成本通常包括能耗成本(仅针对变压器)和检测费用。维护费用来自维护操作、购买维护工具以及维护工程师的薪水。故障成本包括故障组件的维护成本和电力系统的中断费用。报废成本通常包括废料成本和回收成本。一般情况下，维护措施对投资成本、运行成本和报废成本影响很小，而对部件进行维护后，不同的维护模式对故障成本和维护成本的影响会有较大的变化。

在采取有效的维护措施后，降低了故障成本，同时增加了维护成本。因此，在优化维护策略时，平衡维护成本与故障成本具有重要意义。将故障成本和维护成本作为维护策略优化模型的指标。

4.2 故障成本及维护成本

由于意外故障而出现的组件故障会导致两种类型的故障成本。

4.2.1 维护成本RF

维护成本RF来自故障组件的维护操作，计算公式为

(6)

式(6)中：Nt为维护周期的划分周期数；N为变电站中组件的数量；dt为周期t的长度；D为维护周期的总长度；F(t)j为周期t中由组件j引起的维护费用。

4.2.2 中断费用RC

故障组件可能会导致断电事件。电力中断的严重程度可以由中断成本RC来描述，计算公式为

(7)

式(7)中：Cf为单位中断成本，元/(MW·h)；S为变电站状态的总数； EENSS(t)为变电站状态总数S在t时段的EENS，由式(8)估算，即

EENSs=Ps(t)CDsTs

(8)

式(8)中： CDs为状态s的负载削减；Ts为状态s的持续时间；Ps(t)为s在周期t中的状态概率，利用设备的不可用性通过蒙特卡洛方法进行评估。不可用性的计算公式为

(9)

式(9)中：MTTR为平均修复时间，变压器和断路器的MTTR估计为175.2h和87.6h；U(t)j为周期t中组件j的不可用性。

4.2.3 维护成本RM

维护活动涉及修理或更换异常或老化部件，这需要大量的费用来购买新部件、专用维护工具并支付维护工程师的薪水。不同维护方式之间的费用通常是通过对维护费用的历史记录来计算的。

4.3 总费用及维护模型流程

故障成本与维护成本之和定义为总成本AF，公式为

AF=RF+RC+RM

(10)

在此基础上，通过选择最优的维护策略，建立CBM优化模型的目标，维护策略流程如图 4所示。

图 4 维护策略优化流程Fig.4 The procedure of maintenance strategy optimization

由图 4可知，维护策略流程具体步骤如下。

(1)根据电气主接线图及各部件的互连关系，将变电站划分为不同的维护单元。

(2)异常组件的维护方式取决于故障或缺陷的位置和严重程度。在此基础上，提出了替代维护策略。

(3)由HI和寿命降低因子计算组件的失效率。

(4)计算不同备用维护策略成本，并选取总成本最小的最优维护策略。

5 案例分析

5.1 案例介绍

图5 为220kV变电站的电气主接线图。该变电站有3个并联的电流路径，每个路径由1个变压器和3个不同电压等级的断路器组成。电力从220kV一侧传输到110kV和10kV一侧。变压器T1的类型为SFPSZ7-120000/220，T2和T3的类型为SFSZ10-180000/220。3个220kV断路器(HDL1，HDL2和HDL3)的类型为GL314，3个110kV断路器(MDL1，MDL2和MDL3)的类型为LTB145D1/B，3个10kV断路器(LDL1，LDL2和LDL3)的类型为10-VPR-32C(D)。将断路器用于连接总线和变压器。所有正常条件分量的ISE为100。为简化计算，假定线路和总线的失效率为1。

图 5 变电站电气主接线图Fig.5 The electric main wiring diagram of the substation

表 1 显示了不同维护方式的维护成本和修复成本。这些成本是根据维护操作的历史记录估算的。不同维护方式的平均停机时间如表 2所示。不同维护方式的寿命降低因子如表 3所示。单位中断成本为12200元/(MW·h)，采用国内生产总值法(GDP)进行计算。

根据变电站的配置以及变压器和断路器的互联关系，将变电站分为3个维护单元，如图 5所示。每个单元都是一条路径，其中包括1个变压器和3个断路器。

在日常检查中，维护工程师在一个变压器和两个断路器中发现了一些缺陷，所有这些组件都需要维护。检验数据和测试数据的信息以及这些组件的状态如表 4所示。根据缺陷的位置和严重程度，应通过维护模式B维护T2和MDL2。HDL1应采用维护模式A进行维护，因为基础沉降将会对整个设备产生影响。

表 4 组件的检验数据和测试数据Table4 Inspection data and test data of the components

基于此，根据样本数据和第3节的方法，分别估算了变压器和断路器的参数K、C、Cons、α和β，结果如表 5所示。基于HI和年龄降低因子的失效率计算结果，如表 6所示。

表 5 参数计算结果Table5 The parameters calculation result

表 6 失效率计算结果Table6 Calculation result of failure rate

5.2 维护策略

维护部门要求在15d内消除所有部件的缺陷。为了降低变电站的风险，负荷调度部门降低了变电站的负荷水平。这15d平均有功功率估计为215MW，满足变电站的N-1原则。为进一步说明所提策略的先进性，此处选择文献[12-13]作为比较对象。基于此，设计了5种维护策略，如表 7 所示。

表 7 5种可选策略Table7 Five alternative strategy

策略 1 和策略2为所提策略优化结果，为了保证变电站的供电能力，两个检修单元应有序检修，而不能同时检修。第3种和第4种策略分别对应了文献[12]和文献[13]，它们不考虑维护单元，按顺序对这些组件进行维护，因此修复时间较长。策略5 仅作为比较参考，该策略选择同时维护3个组件，维护停机时间仅为5d。

5.3 维护策略的选择

采用第3节的方法计算了每个维护周期内3种不同时期的成本，并最终估算出每种策略的总成本。策略1计算结果如表 8所示。

表 8 策略1的计算结果Table8 Calculation results of strategy 1

同理，可得其余策略的总成本，计算结果如表 9所示。策略1 在5种策略中总成本最小，为最优策略。

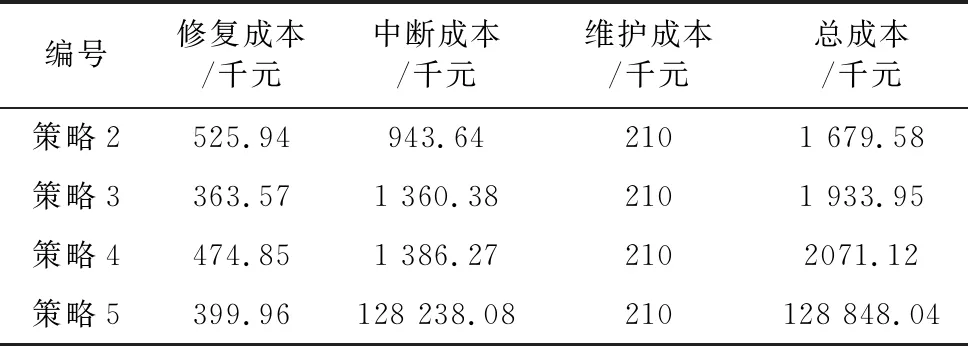
表 9 其他4种策略的运算结果Table9 Calculation results of other 4 strategies

从表 9 的计算结果可以看出，由于确定了异常部件的维护方式，所以各备选策略的维护成本相同。但是，策略1和策略2的中断成本明显小于其他策略。在策略3和策略4中，分别对T2和MDL2进行维护，增加了变电站的维护时间和潜在风险。因此，组件一起维护可以明显降低中断成本。另外，策略5的计算结果表明，同时进行所有设备的维护是不合理的。策略5的中断成本远远高于其余策略，原因是变电站有功功率超出T3的输电能力。因此，应有序地维护不同维护单元中的组件。

策略1与策略2的区别在于异常组件的维护优先级。计算结果表明，策略1优于策略2，因为其修复成本和中断成本较低。通过对原因的进一步分析，维护2个单元的可靠性低于维护1个单元。优先安排T2和DL2的维护行动，可以更好地提高可靠性，降低组件和变电站的风险。因此，在优化维护策略时，应优先维护失效率较高的部件，以达到总成本更低的目的。

6 结论

针对当前传统的基于状态的电力设备维护策略在维护策略不足等问题，提出了一种基于多源数据分析的变电站状态的CBM策略优化方法。引入了维护单元的概念，通过变电站电气主接线图和不同组件之间的关联可将变电站划分为不同的维护单元，而后引入了基于健康指数(HI)和寿命降低因子的失效率计算模型，最后建立了LCC理论的CBM优化模型并进行了针对性实验，得出以下结论。

(1)维护单元概念的引入可以达到对该组件内组件进行统一维护而变电站整体影响较小。

(2)基于失效率计算模型能有效地利用更多的数据来估算模型中参数从而达到更高的精准度。

(3)基于LCC理论模型建立的CBM优化策略能有效地减少变电站的维护时间，降低维护成本，并提高变电站的供电可靠性。