基于计算流体力学-离散单元法耦合的粗糙壁面颗粒趋壁沉积过程的数值模拟

刘 岩，秦 攀，洪文鹏

(1. 中电华创(苏州)电力技术研究有限公司，苏州 215123； 2. 东北电力大学能源与动力工程学院，吉林 132012)

细微颗粒物在日常生活和生产中普遍存在。粒径小于10μm的颗粒能够进入上呼吸道甚至深入肺部，引起呼吸系统疾病[1-2]；而10μm以上的颗粒沉积在室内会导致材料退化，如艺术品和电子设备受损[3]，如何降低室内颗粒物浓度成为当前建筑环境研究领域的热点问题之一。建筑物中的通风和空调系统作为室内外空气交换的主要场所，室内颗粒浓度与颗粒在通风和空调系统管道中的输运及沉积现象密切相关[4]。

近几十年来，许多学者从理论、实验和模拟3个方面对粗糙壁面颗粒沉积机理和求解方法开展了大量研究。发现虽然通过理论[5-6]和实验[7-10]得到的颗粒沉积速率和无量纲弛豫时间关系曲线变化趋势一致，但是无量纲沉积速率差值最大达到1～2个数量级[4-9]。理论研究更多是根据实际经验得到半经验解，而实验很难捕捉到所有重要信息，因此，仅通过理论和实验对粗糙壁面颗粒行为研究具有一定挑战。

目前计算流体力学(computational fluid dyna-mics，CFD)对颗粒沉积应用比较广泛，能够提供更详细的流场和颗粒行为信息。采用直接数值模拟、大涡模拟和分离涡模拟方法进行求解计算成本过高，只有部分学者采用此方法对粗糙壁面表面粗糙度、颗粒再悬浮和多层沉积过程进行研究[11-14]。相比以上3种方法，雷诺应力模型应用最为广泛。学者们主要通过改变粗糙元布置方式[15-18]、形状[19-20]、间距和高度[18，21]，探索粗糙壁面多层沉积、颗粒沉积规律和不同位置沉积情况，还有学者采用Hertz-Mindlin接触模型对大粒径、非球体颗粒运动规律进行初探[22-23]。

然而，以往对粗糙壁面颗粒沉积的研究大多简化了颗粒沉积条件，即假设颗粒接触壁面就会无条件发生沉积或没考虑黏附作用，但实验研究表明，即使是微米级颗粒，也会出现反弹现象，并且微米级颗粒间还存在黏附作用[24-25]。

因此，现采用计算流体力学-离散单元法(discrete element method，DEM)[26]耦合方法，模拟颗粒沉积过程，充分考虑颗粒-颗粒、颗粒-壁面间的接触碰撞、反弹和黏附作用，对光滑和粗糙壁面颗粒沉积进行模拟，分析颗粒粒径、碰撞力、黏附力和二次流对颗粒沉积的影响，探索粗糙壁面颗粒趋壁沉积行为机理，不仅对促进气固两相流动与沉积规律的研究有一定的理论依据，还对室内空气品质的改善和其他相关应用具有一定的指导意义。

1 动态沉积模型

颗粒在壁面附近运动包括在流场中运动、沿壁面滑动和与壁面接触黏附或反弹3个过程，采用CFD-DEM耦合模型进行模拟，首先在Fluent中对气相进行求解，随后在EDEM软件中对颗粒相进行计算，通过Fluent中UDF和EDEM中API接口实现耦合连接，部分耦合代码如图 1所示。

图 1 部分耦合代码Fig.1 The part of the coupled code

1.1 气相模型

气相视为不可压缩流体，流体连续性方程和动量方程分别为

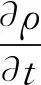
(1)

(2)

式中：ρ为空气密度；t为时间；u为空气速度；μ为空气动力黏度；V为CFD网格单元的体积；FD为曳力，是颗粒物在流道中运动和沉积的主导作用力。

1.2 颗粒相模型

1.2.1 颗粒运动模型

颗粒受力包括重力、曳力、Saffman升力、颗粒-颗粒、颗粒-壁面之间的碰撞力和黏附力，颗粒发生碰撞和黏附及其受力示意图如图 2所示。

图 2 颗粒碰撞、黏附和受力示意图Fig.2 Schematic diagram of particle collision，adhesion and force

颗粒的运动方程为

(3)

式(3)中：mp为颗粒质量；up为颗粒运动速度；FG为重力；Fad为黏附力；FC为颗粒受到的碰撞力；FS为Saffman升力；FAr为阿基米德浮力。

1.2.2 JKR接触模型

采用Hertz-Mindlin with JKR Cohesion[27]接触模型，考虑接触区域内范德华力对颗粒-壁面、颗粒-颗粒间的黏附作用，粒子黏附产生的力基于重叠量、相互作用参数和表面能，公式为

(4)

(5)

式中：E*为当量弹性模量；R*为当量半径；α为接触半径；γ为表面能；δ为颗粒间重叠量，当颗粒与壁面接触时，视壁面为无穷大颗粒。

2 模拟条件

计算区域是三维底面布置矩形横肋的粗糙流道(160 mm×20 mm×20 mm)，底面均匀布置7个间距为20 mm的横肋粗糙元结构，粗糙元高度e为2mm，计算域如图 3所示。为了减少计算量和仿真时间，采用边界函数分布法对入口速度和湍动能进行初始化；出口采用自由出流边界；在距离流道入口3R(R为颗粒半径)处均匀释放颗粒，当颗粒全部沉积或流出流道视为模拟结束，主要模拟参数如表 1所示。

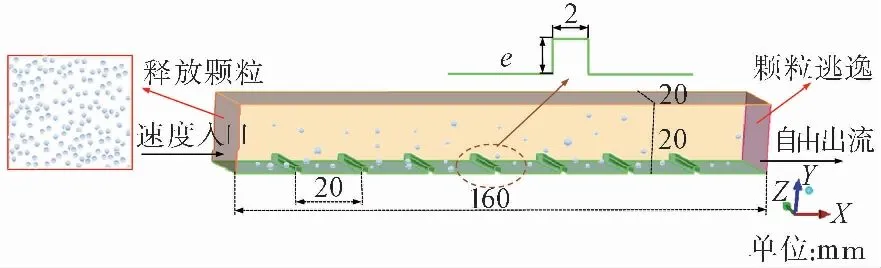
图 3 计算域Fig.3 The computational domain

表 1 主要模拟参数Table1 The main simulation parameters

使用ICEM软件对模型进行网格划分，粗糙结构的存在使得流场变得复杂，为准确预测颗粒-壁面的相互作用，对近壁面网格进行加密，第一层网格高度为0.05mm，第一层网格质心到壁面的无量纲距离y+为1.2，增长因子为1.2，结构化网格，考虑到计算代价和准确性等因素影响，经网格无关性验证，如图 4所示，采用网格数为59.8×104的模型进行计算。

图 4 网格无关性验证Fig.4 Grid independence verification

图 5 粗糙结构间气流速度分布Fig.5 The air velocity distribution between rough structures

3 模型验证

3.1 湍流场

精确的湍流场是研究颗粒沉积的基础，有研究表明，流场在第Ⅳ个粗糙结构后趋于稳定。因此选取第Ⅵ和第Ⅶ个粗糙结构间气流速度与实验值[28]进行对比，发现吻合较好，如图 5所示，说明采用雷诺应力模型可以准确预测粗糙流道的湍流场。

3.2 数值算法验证

(6)

式(6)中：h为计算域高度；U0为平均流速；Ndep为壁面沉积的总颗粒数目；Nin为进入流道总颗粒数；u*为湍流摩擦速度；L为计算域的长度。

基于流动内时间尺度的无量纲颗粒弛豫时间[30]为

(7)

式(7)中：S为气固密度比；dp为颗粒直径；Cc为坎宁汉系数；ν为空气动力黏度。

为了验证数值算法的正确性，将光滑壁面颗粒无量纲沉积速率与经典模拟[31-32]和实验值[33-34]进行对比，吻合较好，如图 6所示。因为颗粒与壁面为点接触，因此采用的JKR模型同样可以准确预测粗糙壁面颗粒沉积情况。

4 结果与讨论

4.1 气相流场

微米级颗粒受流场影响程度较大，研究颗粒在流场中的运动情况，首先对流场进行分析。

从图 7光滑和粗糙流道湍动能和流线分布可以看出，气流在流经粗糙结构时边界层发生分离，使粗糙结构附近出现大小不一的湍流旋涡，增加对颗粒的卷吸作用，并且有垂直于流动方向的湍流脉动速度，颗粒趋壁速度得到提高，粗糙流道最大湍动能达到光滑流道湍动能的6.97倍，而光滑流道的流线几乎与X轴平行，更易携带颗粒流出流道，不利于颗粒沉积。

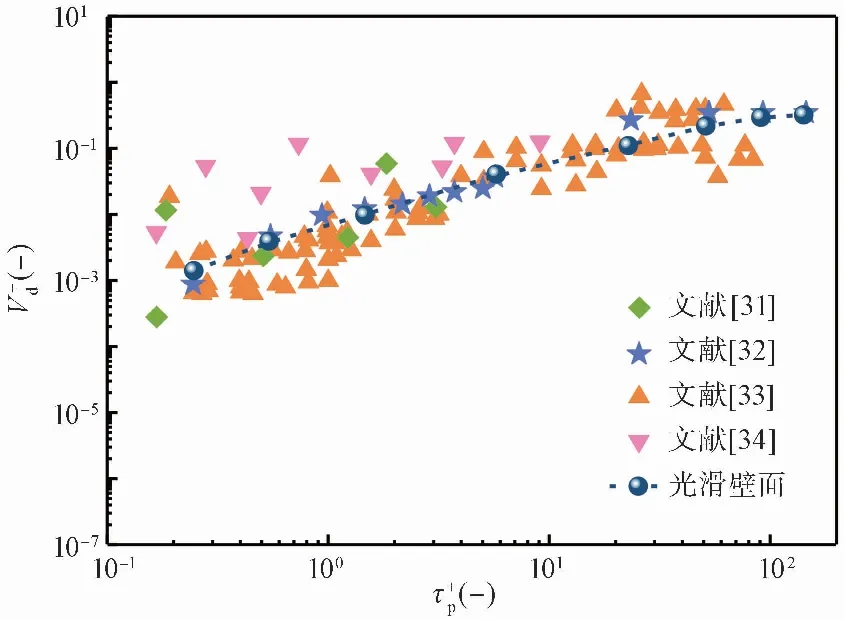
图 6 光滑壁面无量纲沉积速率对比验证Fig.6 Comparison and verification of non-dimension deposition velocity on smooth surface

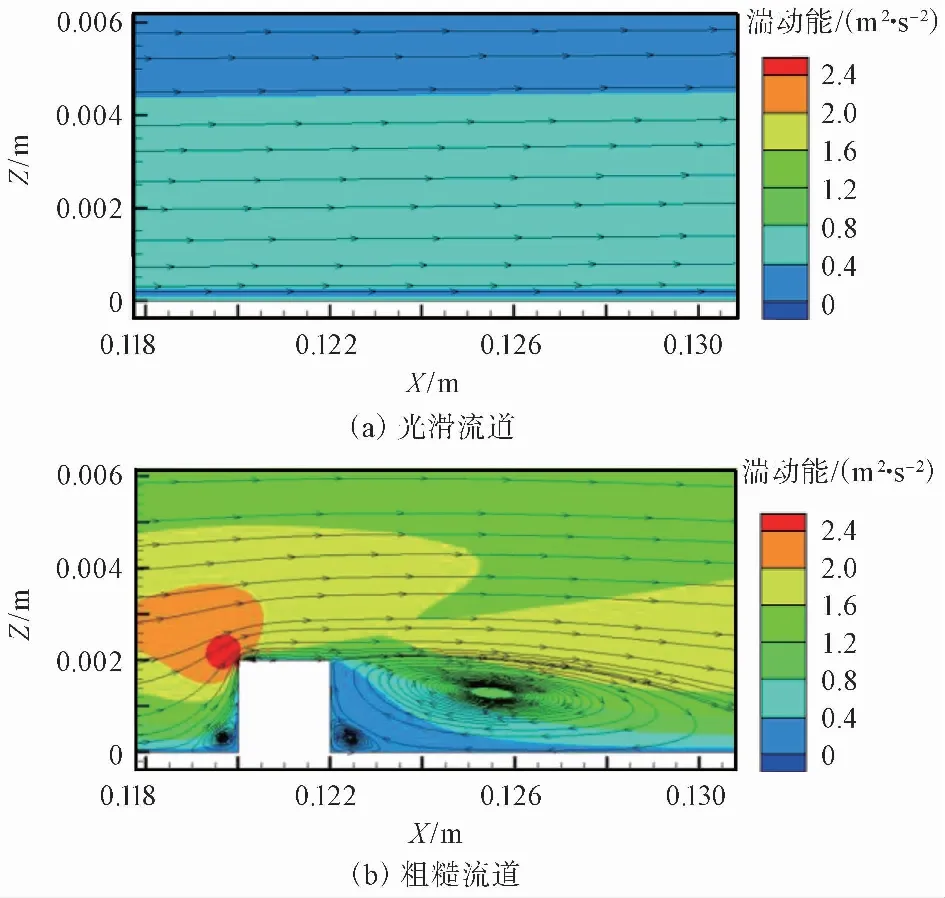
图 7 光滑和粗糙流道湍动能和流线分布Fig.7 Turbulent kinetic energy and streamline distribution on smooth and rough surface

4.2 粗糙结构对颗粒沉积影响

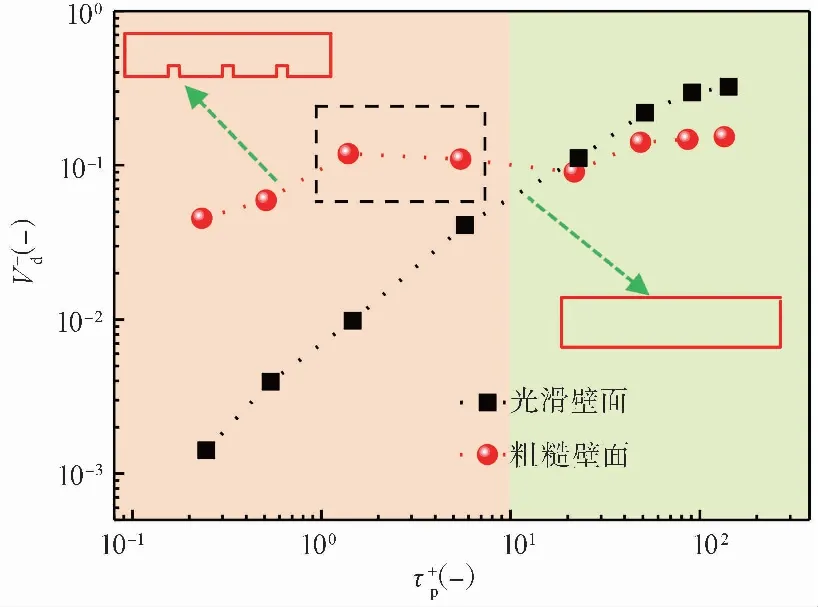
图 8 粗糙和光滑壁面颗粒无量纲沉积速率对比Fig.8 The comparison of particle deposition velocity on rough and smooth surfaces

图 9 2μm和3μm颗粒运动轨迹Fig.9 2μm and 3μm particle trajectories

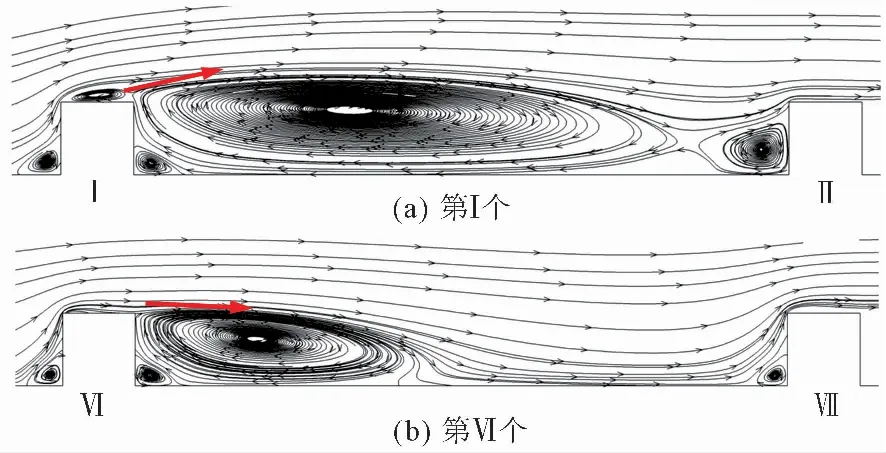
图 10 第Ⅰ个和第Ⅵ个粗糙结构附近旋涡回流Fig.10 Vortexes near the first and the sixth rough structure

图 11 50μm颗粒运动轨迹Fig.11 50μm particle trajectory

4.3 碰撞力和黏附力对颗粒沉积影响

为进一步探索颗粒沉积机理，首先从颗粒能够与壁面接触数进行分析，经统计，50μm颗粒与壁面接触数为2μm颗粒与壁面接触数的8.9倍，而50μm颗粒沉积速率仅是2μm的3.4倍，颗粒运动情况不仅受气相流场影响，还与颗粒-壁面间碰撞力和黏附力有关。图 12(a)、图12(b)分别为2、5μm颗粒-壁面间黏附力和碰撞力对比情况，对于2μm的较小颗粒而言，其与壁面碰撞力和黏附力大小相当，因此旋涡卷吸是使小颗粒沉积的主要因素；而对于50μm相对粒径较大颗粒，在0.05s，颗粒全部发生沉积或沿壁面滑动，在0.05s之前，颗粒-壁面碰撞力明显大于黏附力，说明颗粒-壁面碰撞是使颗粒沉积速率减小的主要原因，而黏附力和自身惯性是颗粒沉积的主要因素。

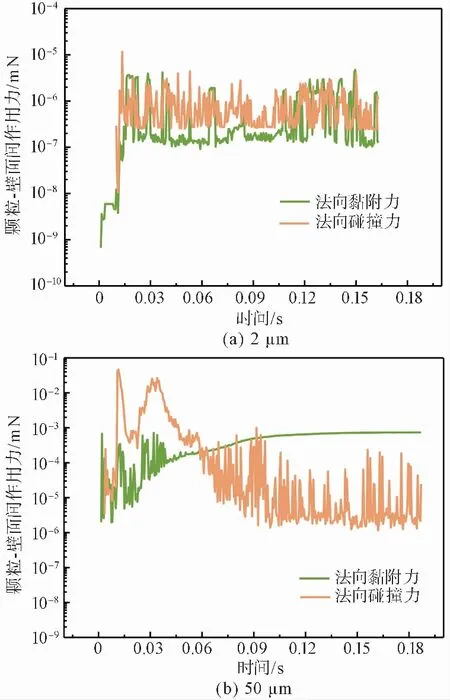
图 12 颗粒-壁面作用力对比Fig.12 Comparison of the particle-wall forces

4.4 二次流对颗粒沉积影响

由于法向和展向壁面的剪切作用，气相在沿着主流方向运动过程中发生边界层分离，使得在垂直于流动方向横截面上压力分布不均，流道壁面与流道中心之间压力不平衡，压力梯度驱使气相在流道壁面与流道中心之间对流流动，形成二次流，其现象如图 13所示。由于粗糙元的存在使得粗糙流道只在底部产生两个明显的旋涡，卷吸颗粒使其在底面两侧附近聚集。为了更直观地看到二次流对不同粒径颗粒沉积情况的影响，分别选取粒径为5、20、50μm的颗粒进行分析，颗粒沿X方向上的沉降情况的概率密度ζ(颗粒沉积数/颗粒总数)分布如图 14所示。由此看出5μm颗粒均匀分布在壁面两侧，壁面中间位置基本不发生颗粒沉积，20、50μm的颗粒沉积绝大部分发生在粗糙壁面两侧附近，在壁面中间位置会有少部分沉积，在两侧壁面附近，50μm颗粒的概率密度将达到5μm的34倍。这是因为小颗粒由于自身惯性低而容易受到湍流二次流的影响，随着颗粒直径的增大，受重力和惯性的影响越大，越不容易被涡卷吸，从而发生沉积。

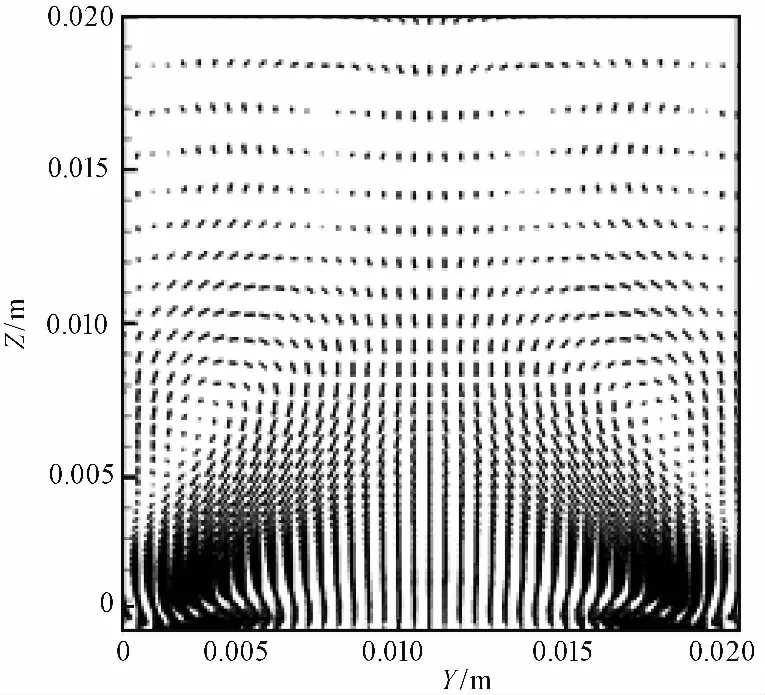
图 13 粗糙流道二次流矢量分布Fig.13 The secondary flow vector distribution in rib-roughened channel

图 14 颗粒沿X方向上沉降情况的概率分布Fig.14 The particles probability density distribution in the X direction

5 结论

采用计算流体力学(CFD)-离散单元法(DEM)耦合模型对三维矩形光滑壁面和布置横肋粗糙壁面的颗粒沉积进行模拟计算，分析了单分散颗粒沉积过程，在研究分析过程中得出在涡扩散碰撞区，粗糙壁面颗粒沉积速率大于光滑壁面颗粒沉积速率，特别是对于粒径为2μm的颗粒，粗糙壁面颗粒沉积速率达到光滑壁面的32倍；在惯性缓冲区，由于大颗粒碰撞作用较为强烈，使得粗糙壁面颗粒沉积速率反而小于光滑壁面颗粒沉积速率。由于二次流的影响，使得较小粒径颗粒均匀沉积在壁面两侧，中间位置几乎不发生沉积，而对相对粒径较大颗粒，大部分颗粒沉积在壁面两侧，有少部分颗粒沉积在壁面中间位置，并且在壁面两侧，50μm颗粒的概率密度将达到5μm的34倍。