煤层注水中湿润半径和渗流速度演化规律的探索
2021-06-24吴金随陈学习张润畦
吴金随,陈学习,张润畦
(1.华北科技学院 安全工程学院,北京 东燕郊 065201;2.华北科技学院 安全监管学院,北京 东燕郊 065201)
0 引言
煤层注水是煤矿开采中降低回采工作面产尘量的重要手段,是从根本上解决矿井粉尘问题的有效措施。同时,煤层注水在防治瓦斯灾害、减少冲击地压、软化煤体等方面也具有显著作用[1-3]。国内外许多学者研究了煤层注水中湿润半径的渗流规律[4-6]。宋维源等[7]忽略煤层中瓦斯含量变化的影响,研究了煤层注水中渗流基本规律,建立了厚煤层和薄煤层注水的渗流模型。孙超和宋维源等[8]研究了煤层注水过程中水气驱替理论,得到了平面平行流湿润半径的变化规律及流速的关系式。梁宝霞等[9]研究了高瓦斯薄煤层注水平面平行流模型。在假定湿润半径为常数的前提下,推导出薄煤层湿润半径与时间的函数关系式。张茂增等[10]基于双重空隙介质渗流理论,对煤层注水的机理进行了论述,没有给出解析式。朱红青等[11]提出脉动注水增透技术,从微观机理上对脉动注水原理和疲劳裂纹起裂扩展过程进行了研究,没有考虑湿润半径和注水时间的关系式。郭红玉等[12]通过实验得出:随着含水饱和度的增大,渗透率逐渐降低,启动压力梯度逐步增大,渗透率越低的样品对含水饱度越敏感的规律。从理论上解释了煤层注水抑制瓦斯涌出的原因。孟筠青等[13]重点研究了煤层高压脉动注水在防治煤与瓦斯突出中的应用前景。曹家琳等[14]给出了采动影响下工作面深孔注水非线性渗流规律。曾现策等[15]使用 Comsol 软件模拟了单孔煤层注水,忽略毛细管力、重力、水气与孔隙介质之间物理化学反应,只考虑单相情况,对气液两相流没有研究。黄腾瑶等[16]考虑到注水压力对湿润半径的影响,得到了其经验关系式,有两个实验参数。汪文瑞等[17]在注水模型中引入分形维数。陈绍杰等[18]对煤层注水和瓦斯抽采过程进行分析,建立了煤层注水与瓦斯抽采单相渗流的数学模型。还系统的分析了活塞式驱替下水与瓦斯分界面运动规律,推导出非活塞式驱替下平面径向渗流含水饱和度分布方程,建立了煤层注水驱替瓦斯两相渗流模型。邓志刚[19]指出:采动过程中煤层渗透率是有明显变化的,没有研究湿润半径演化规律。郭敬中等[20]在煤层注水中应用渗透棒将注水湿润半径从6~8 m提高到了20 m以上。程为民等[21]总结了二十年来粉尘防治理论及技术取得的成果,并提出了未来发展方向。
综上所述,为了深入研究煤层注水中渗流规律,学者们结合实验数据总结出了经验公式,但没有给出渗流速度和浸润半径之间有明确物理含义的参量表达式。本文以渗流力学为基础,从两相流的理论出发,建立煤层注水湿润过程中新的渗流方程,得了煤层注水压力、湿润半径、渗流速度等物理量随时间演化的解析表达式。与工作面深孔注水非线性渗流规律对比,给出了新的理论适用范围。结合郑煤集团白坪矿采煤工作面实测参数,该模型给出了煤层注水后润湿半径的理论预测值。
1 平行平面流煤层注水渗流模型
煤层注水的过程就是沿煤层孔隙将水注入煤体内部的过程。由于注水煤层厚度远小于采掘工作面走向长度,该力学模型中液体在注水区的运动可视为平面平行流[16],如图1所示。因此,可以用平行平面流模型来研究煤层注水的渗流过程。
为简化模型,本文假定液态水和瓦斯气体的渗流过程均服从达西定律。假定注水的地层都具有均质、等厚、各向同性的特点。钻孔前,地层各处压力相等,且为原始地层压力。假设储水区和含气区均为单相,保证在气液流动过程中重力作用和毛细管张力作用的影响极小,都可以忽略不计。假设注水过程中液态水和瓦斯气体均不与煤层的孔隙介质材料发生物理化学反应,即假设“水驱气过程”为完全驱替过程(活塞式驱替过程)。
由此,本文建立了“平行平面流”的煤层注水渗流模型,如图1所示。
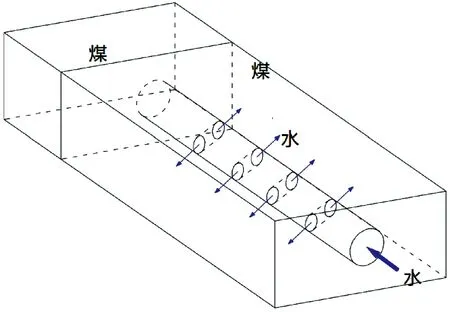
图1 煤层注水模型示意图[16]
在定压渗透的情况下,为简化计算,本文设末端压强为0,则初始条件和边界条件可写为:
(1)
式中,P为压强;Pw为注水压强;v为流速;rw为注水孔半径;x为水头位置。
当注入的液态水在管中流动时,假设管两端的压强差由Pw变到0的过程为定压过滤过程。根据达西定律可得:
(2)
式中,k为渗透率;μ为液体粘滞系数。
由式(2)可得:
(3)
式中,ΔP=P-Pw。
由式(3)对t求导:
(4)
由Dupuit-Forchheimer关系式:
(5)
式中,Φ为孔隙率。
联立式(4)和(5)可得:
(6)
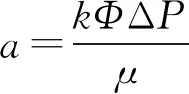
(7)
式(7)两边分别对dt和dv积分可得:
(8)
进一步可解得流速随时间的变化关系式:
(9)
由式(9)可知,流速、压强、渗透率、孔隙率等参数都是非线性变化的,其演化规律有一定的复杂性。
联立式(3)和式(5)得:
(10)
对式(10)两边积分得:
(11)
可解得:
(12)
由式(12)可知,湿润半径随时间变化的函数关系,以及压强随时间变化的函数都是非线性的。
2 理论模型分析
曹佳琳研究采动影响下工作面深孔注水非线性渗流规律,给出了解析式[14]。
(13)
(14)
式中,s为煤体的贮水系数项,m-1;Fm为煤体最大湿润水分增值,m3;a为压力修正系数;bS为贮水识别系数;P为润湿压力,Pa。
我们用(12)式湿润半径和注水时间的预测值与非线性模型[14]进行对比,如图2所示,两种模型湿润半径与注水时间的预测值符合的很好。在模拟过程中,使用了非线性模型[14]中的基本参数P0=0 MPa,Pw=10 MPa,Rw=0,k=593×10-3mm2。
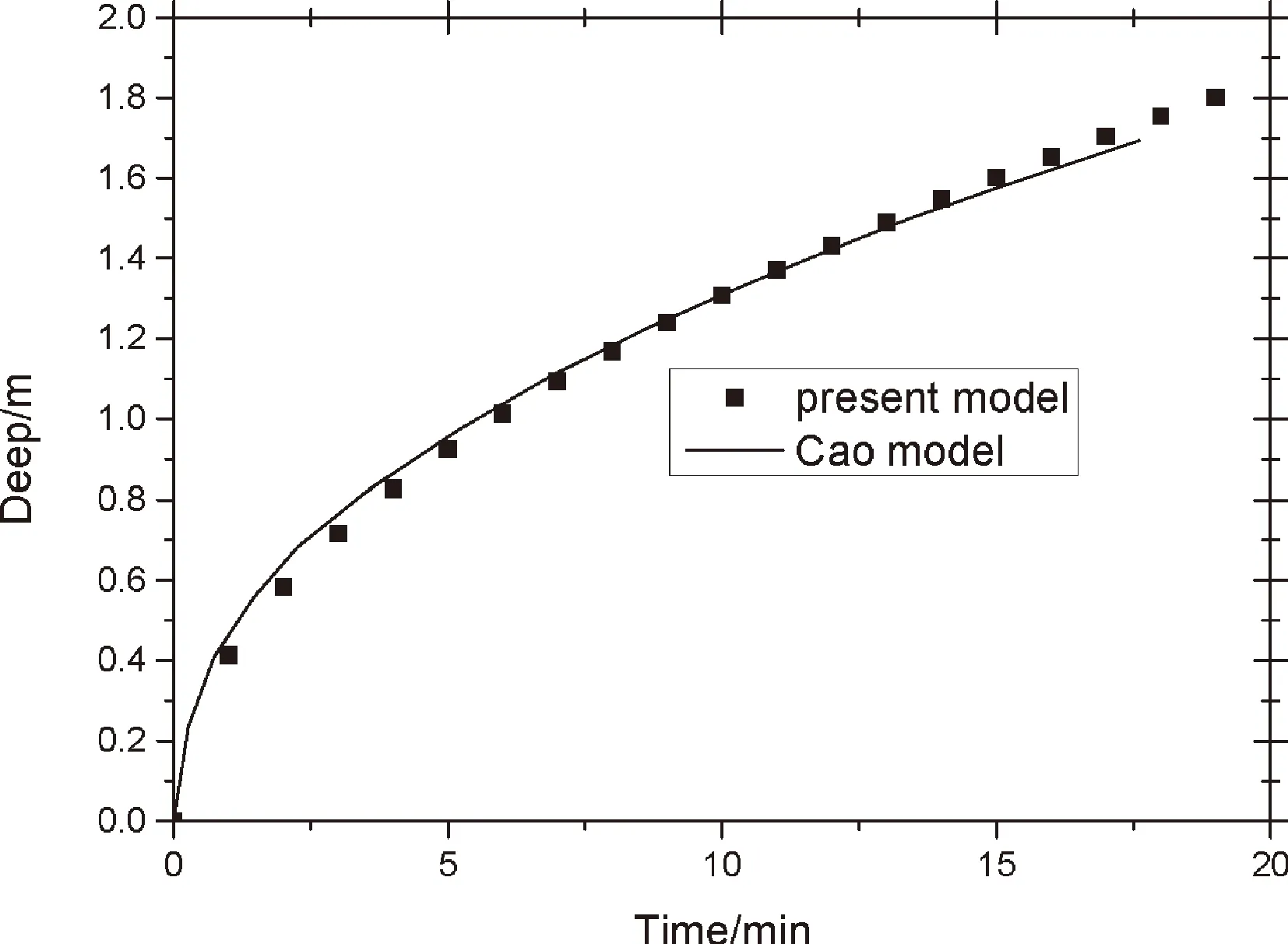
图2 湿润半径与注水时间的规律
从图2中可以看出,薄煤层注水渗透深度的预测值和非线性模型预测值[14],两者之间的差距小于1%。曹佳琳的非线性模型为简化运算,选取特定煤层,但是在实际开采过程中,煤岩的孔隙率与埋藏深度有关,煤层孔隙率对注水渗透深度有很大影响,是一个重要物理参量。 为了更好地研究孔隙率变化对湿润半径的影响,本文根据平行平面流煤层注水渗流模型,结合公式(12)模拟了孔隙率从0.02变化到0.20过程中煤层注水湿润半径的变化规律,如图3所示。具体计算中,假设k=10 md,Pw=4 MPa,P0=0,rw=0.075 m,μ=1.005×10-3Pa·s。
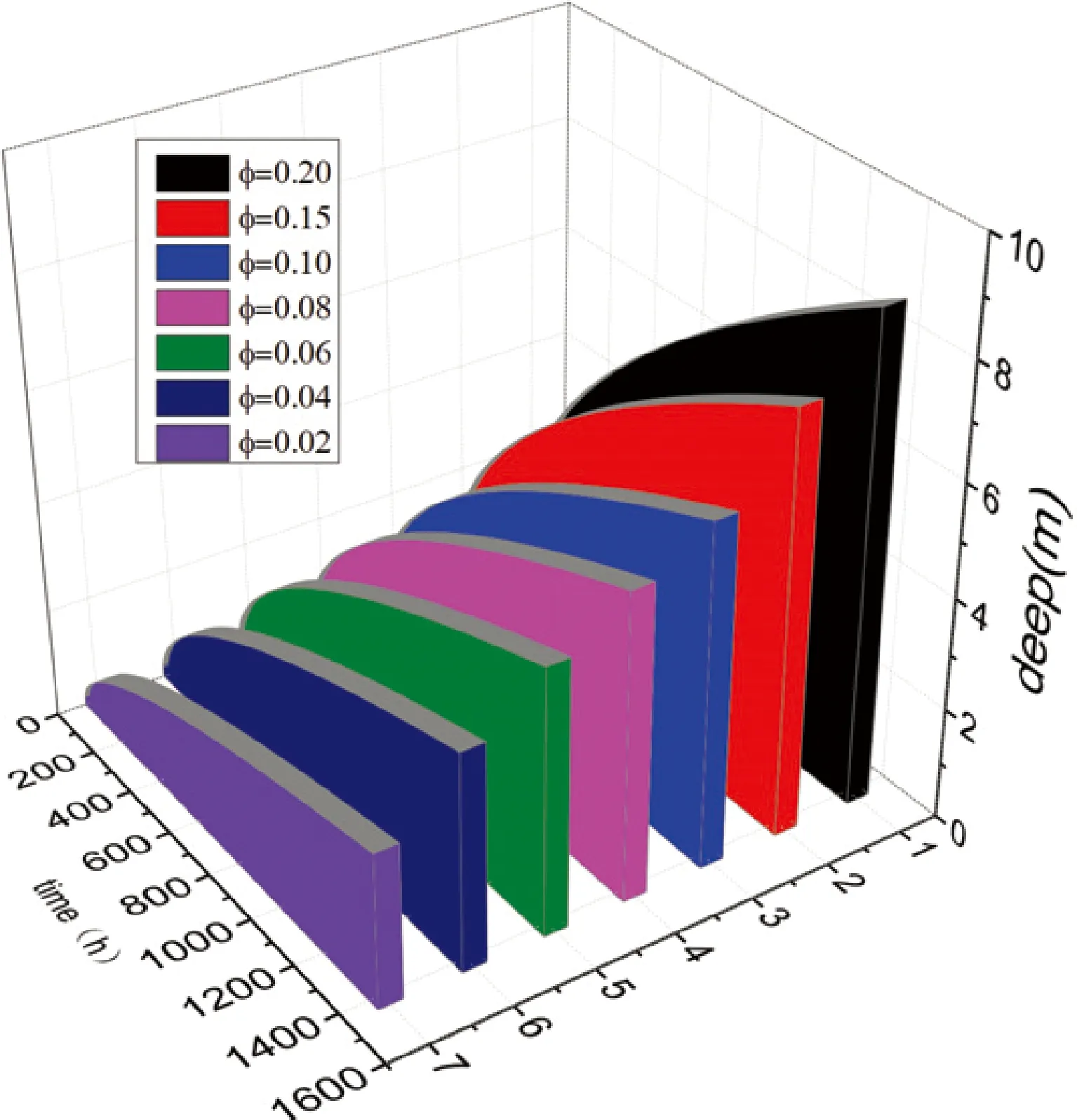
图3 孔隙率的变化对湿润半径的影响
由图3可知,当煤岩的渗透率增加时,注水煤层中水的渗流速度也增加。当煤岩的孔隙率为0.02时,经过1200 h后,计算得到的湿润半径只有2 m。而当孔隙率取0.20时,同样经过1200 h后,计算得到的湿润半径变为8 m,扩大了四倍。图3给出了孔隙率在0.02~0.2范围内变化时湿润半径随时间的变化关系,从图中可以看出相同的注水条件下,湿润半径随孔隙率增加而增加。
下面,本文按煤层渗透性进行分类[18],可分为:非渗透性煤层(渗透率小于0.0001 mm2);低渗透煤层(0.0001~0.001 mm2);中等渗透性煤层(0.001~0.005 mm2);较高渗良好煤层(0.005~0.010 mm2);渗透性极好煤层(大于 0.010 mm2)。邓志刚指出:采动过程中煤层渗透率是有明显变化的[19]。仅通过观测潞安五阳煤矿就发现渗透率从0.042 mm2变化到0.791 mm2,变化了近二十倍[19]。根据式(12)模拟水从低渗透煤层(渗透率为0.0005 mm2)到高渗透煤层(渗透率为0.5 mm2)渗透过程中,煤层注水湿润半径演化规律如图4所示。设同一水平采区中煤层孔隙率为0.05,注水孔半径为0.05 m。设注水区域边界处,Pw=4 MPa,P0=0.35 MPa。 由图4可知,煤层的渗透率对注水半径影响很大。煤层的渗透率越大,注水的湿润半径越大。
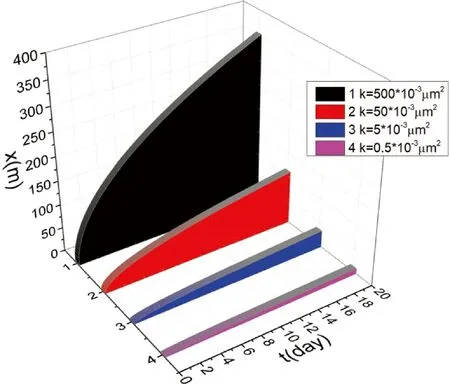
图4 渗透率和湿润半径的关系
图5计算了煤层注水速度随时间的变化规律。煤层孔隙率取0.05时,注水孔半径0.05 m,渗透率0.010 mm2。设注水区域边界处Pw=4 MPa,P0=0.35 MPa。根据注水量换算出水流初始速度v0为 0.5 mm/s,从图5可以看出煤层的注水速度随时间减小。
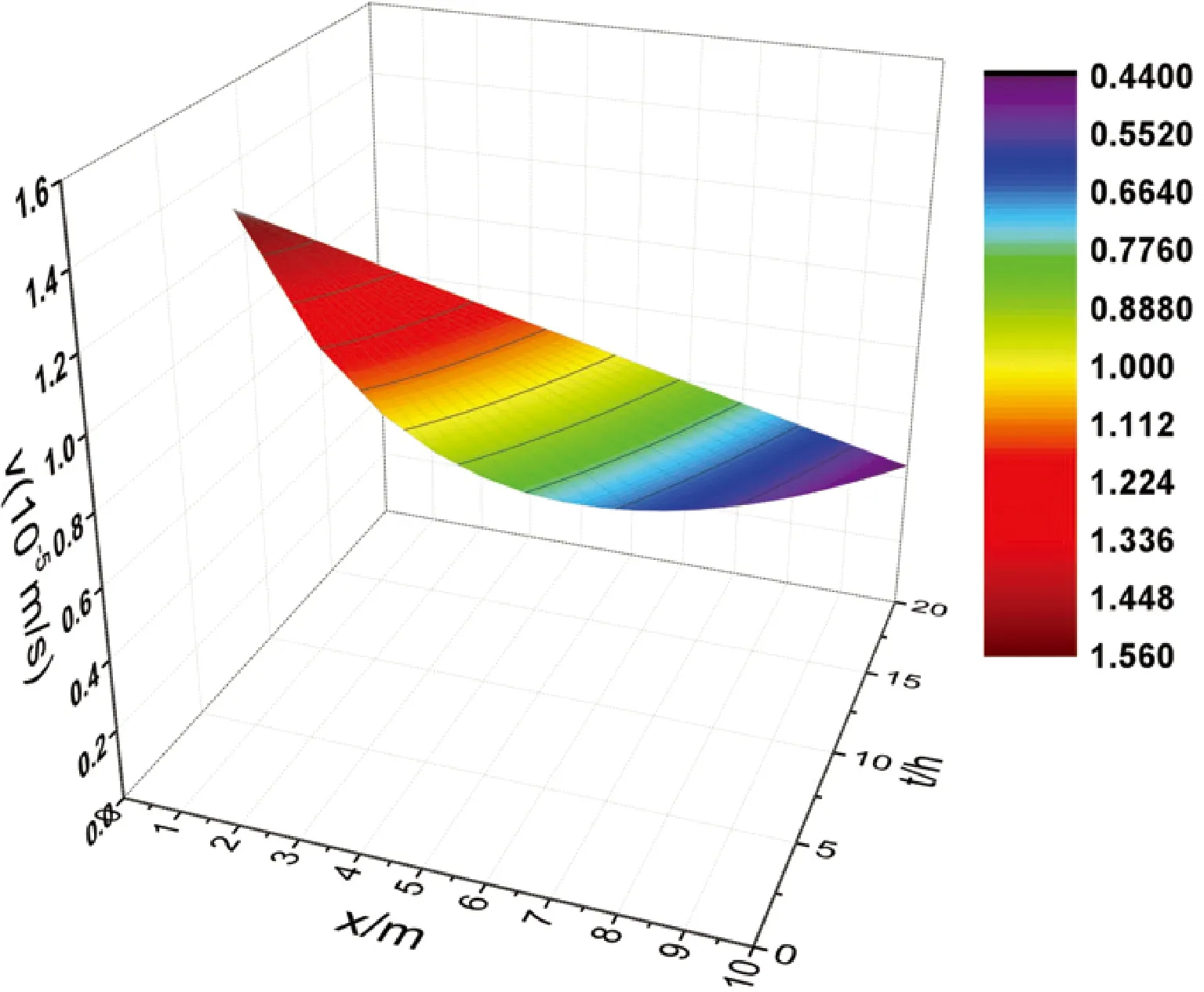
图5 煤层渗透水流速度随注水时间的变化
3 应用
渗透率实验在郑煤白坪矿11221回采工作面进行的,在白坪矿测量了每层孔隙率Φ、注水润湿边界rd、注水压强Pw、煤层瓦斯压强Pg,具体参数见表1。

表1 白坪矿渗透率实验参数值
在待注水煤体的表面上,选取一块没有明显的裂隙相对完好的区域,钻一个直径同采面注水孔(深 3 m)作为测定渗流系数的注水孔;再在其左侧或右侧 (1 m处)钻一个同等直径的孔(深2 m)作为探测孔,用于探测水渗透到该工作面时所需的时间。本轮测试在工作面进行了三次实验,注水时间t分别为 8 min、 8.5 min、9 min,平均为8.5 min。根据式(12)可以计算出渗透率k为
(13)
根据表2中注水量和时间求出单位时间的注水量为

表2 煤层静压注水实施数据统计表
(14)
式中,Q0为总注水量。
再进一步求出注水速度
(15)
式中,L为钻孔长度,d为封孔深度。
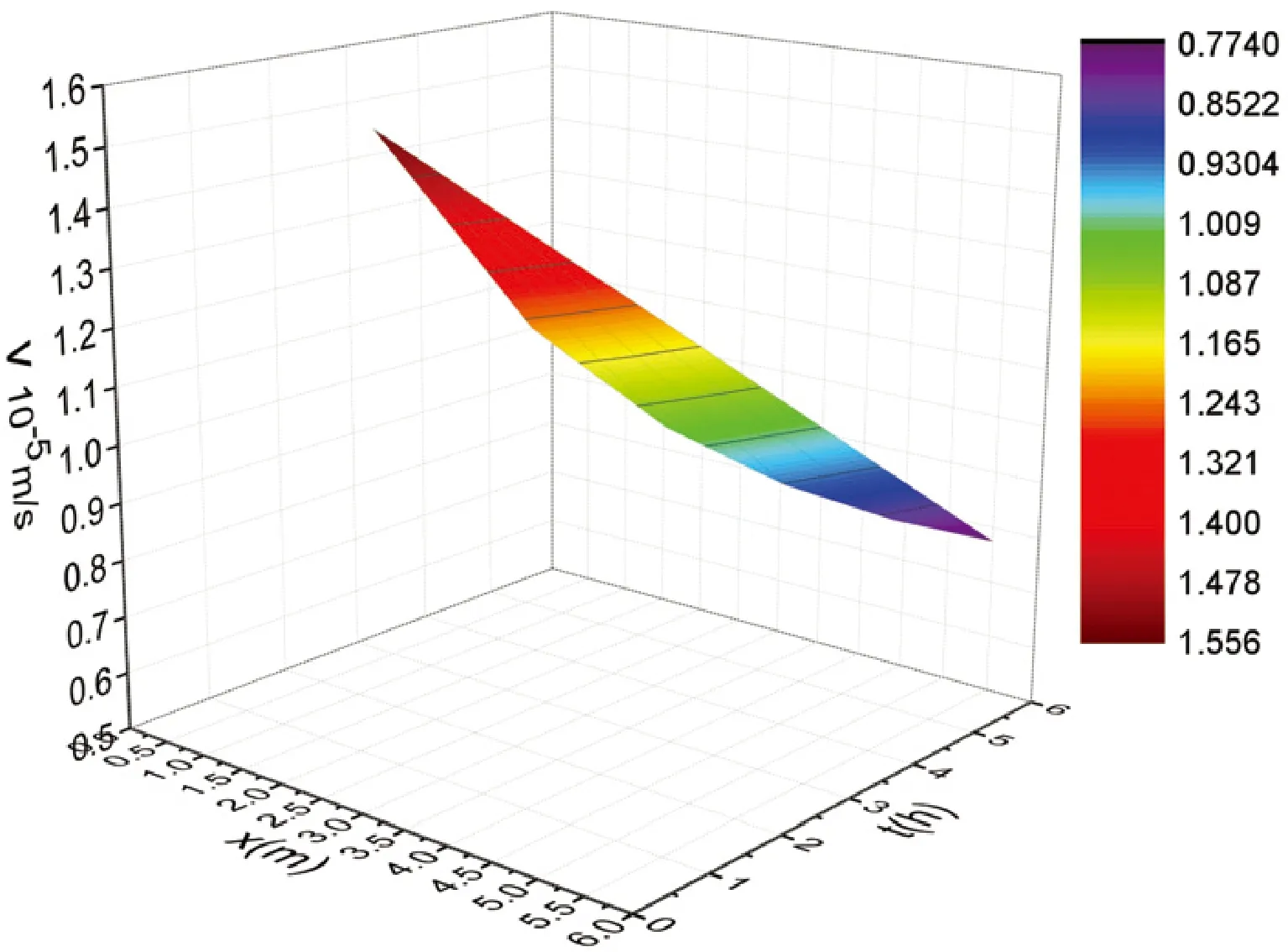
图6 白坪矿渗透水流速度及湿润半径随时间的变化
在郑煤白坪矿进行了煤层注水现场实验,实验结果表明距离注水钻孔5~6 m范围内,煤体含水量大于1%,有一定规律性。因此,认为常规条件下注水的有效湿润半径为5~6 m。本文计算注水后湿润达到6 m需要的时间。
表3和图7研究注水压强对注水时间和湿润半径的影响。当rw=0.075、k=0.01682 mm2、Φ=0.065时, 模拟煤层瓦斯压强Pg恒定取 0.35 MPa时,注水半径与注水时间随注水压强Pw变化的关系。由表3和图7可知:煤层注水压力越大,相同的湿润半径需要的时间越短。
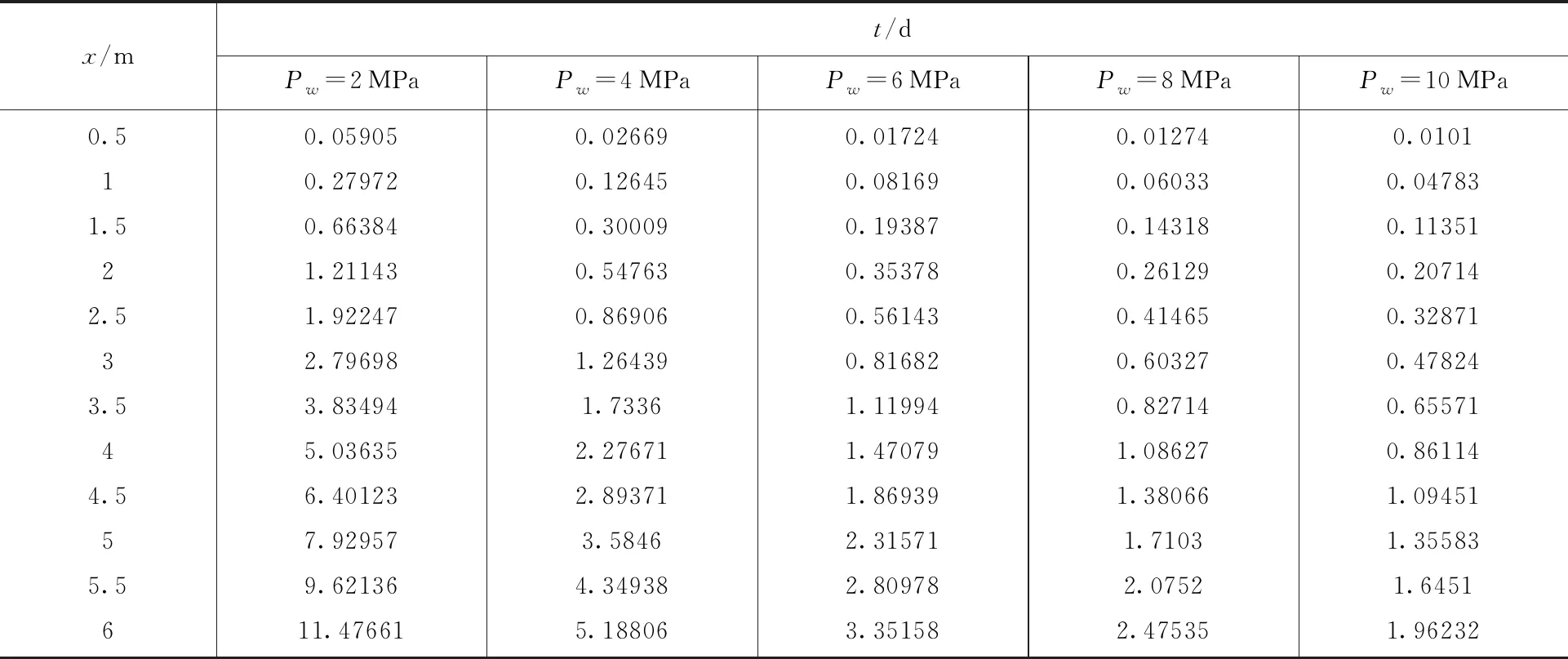
表3 煤层瓦斯压强Pg恒定时注水半径与注水时间的关系
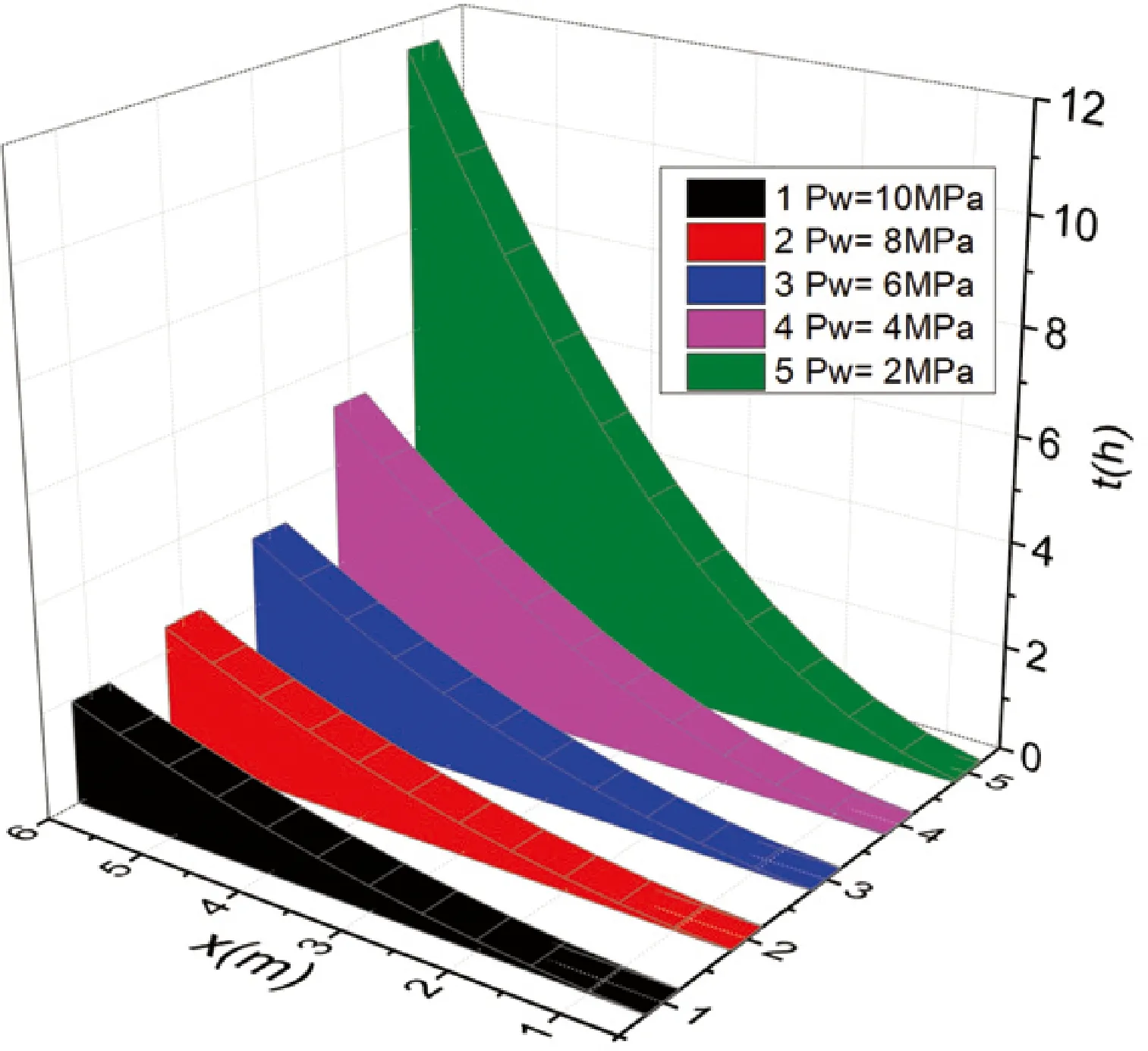
图7 注水压强对注水时间和湿润半径的影响
表4和图8研究 煤层瓦斯压强对注水时间和湿润半径的影响当rw=0.075、k=0.01682 mm2、Φ=0.065时,模拟注水压强Pw恒定取 4 MPa时,注水湿润半径与注水时间随煤层瓦斯压强Pg变化的关系。由表4和图8可知,当煤层压力变大时,要使煤层达到预定的湿润半径,将需要更长时间注水。
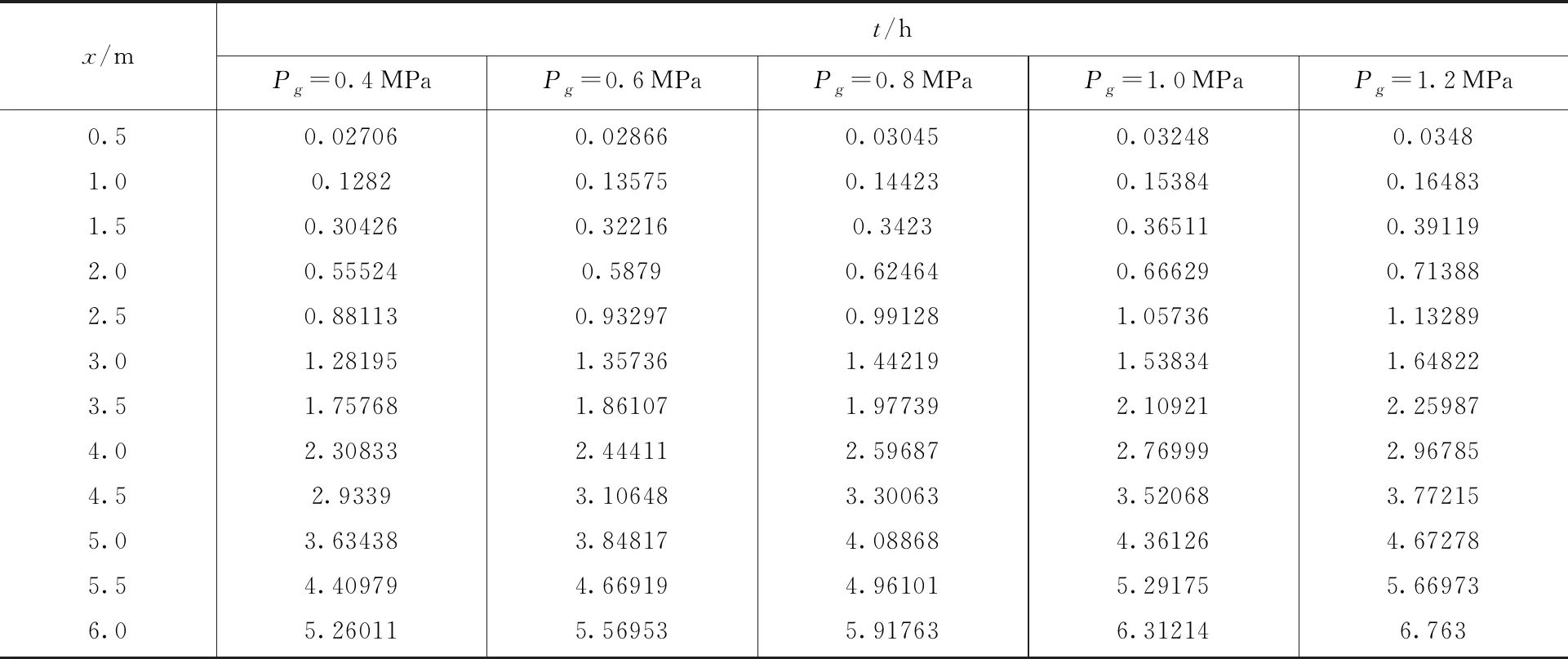
表4 注水压强Pw恒定时注水半径与注水时间的关系
4 结论
(1) 基于达西定律提出的煤层注水渗流力学模型,得到了湿润半径和渗流速度时间、孔隙率等物理量的函数关系式。预测了孔隙率渗透率的变化对湿润半径的影响,以及湿润半径和渗流速度随时间的变化关系。
(2) 将渗流理论应用于白坪矿,根据现场测试数据,计算了白坪矿11221回采面的渗透率和注水速度,预测注水压力和煤层压力变化对湿润半径的影响,并计算了有效湿润半径达到5~6 m所用时间。
(3) 本文没有考虑厚煤层径向流、非线性流以及温度变化等对湿润半径的影响,与复杂问题的精确解相比有偏差,模型还有待改进。
