长九神山灰岩矿开采爆破块度预测研究*

朱子晗，尹岳降，陈 明，魏 东，卢文波，刘建程

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2.中国水利水电第八工程局有限公司，长沙 410004)

爆破作为一种破碎岩体的有效手段，是矿山开采、隧道开挖、铁路和公路建设、水利水电设施建设等工程的主要施工手段。目前在矿山开采中，都存在采矿和碎矿两个环节，很长一段时间内，人们都把它们作为两个独立的过程，忽略了将整个碎矿过程视为一个整体来进行研究，从而影响了总体效益[1]。在露天采石场中，爆破的主要目的是使岩石破碎到合适的尺寸范围，并且需要极大可能地降低大块率和岩粉含量，爆破后岩体块度分布直接影响到后续的装载、运输、破碎过程耗能与成本。因此，事先对爆破后岩石块度大小的分布进行预测对于降低能耗，减小成本有十分重要的意义[2,3]。

20世纪50年代至今，国内外许多学者在爆破块度方面做了大量的研究工作，C Cunningham将Kuznetsov方程与R-R方程结合获得Kuz-Ram模型[4]；刘慧和冯叔瑜基于能量损耗[5]，推导出炸药单耗与块度分布分维数的关系方程式；张宪堂和陈士海考虑块度的二次碰撞[6]，构建了包含损伤变量的块度预测理论模型；周先平和吴新霞等通过建立岩体破碎的临界损伤质点峰值振动速度与爆破块度分布的数学关系式[7]，阐述了基于PPV的爆破块度预测方法；王仁超和朱品光基于森林回归方法建立了爆破块度预测模型[8]，并验证了该模型的可行性。

目前常用的块度预测模型，大多视岩体为均质的连续介质[9]。然而，实际的岩体内存在着节理裂隙等软弱结构面，爆破岩体主要是沿着节理裂隙面破裂而产生的[10]。要想准确预测爆破块度，就必须将节理裂隙的影响考虑其中，但岩体的节理裂隙难以进行确切的描述，常采用经验公式，这就需要针对不同的工程实际对公式内的参数进行优化，使得预测结果更接近实际情况。

基于长九神山灰岩矿料场现场的爆破试验，通过对爆破后爆堆进行人工筛分试验，计算得到平均块度的实测值，并将其与Kuz-Ram模型计算的平均块度值进行比较分析，对模型进行参数优化，并对优化后的模型进行检验。

1 Kuz-Ram预测模型

1.1 模型基本公式

Kuz-Ram模型是南非人C V B Cunningham在前苏联人V E Kuznrtsov研究的基础上提出的。他认为爆破块度服从Rosin-Rammler分布函数。在目前多种块度预测模型中，Kuz-Ram模型因为其具有参数基本已知，计算简便，修正比较容易等优点是目前最常用的爆破块度预测模型。

Kuz-Ram模型的基本表达式由Kuznetsov方程、R-R分布函数和均度不均匀指数部分所组成，具体的计算公式如式(1)～(3)[2,4]

(1)

R=1-e-(X/X0)n

(2)

n=(2.2-14W/d)(1-e/W)[1+(m-1)/2]L/H

(3)

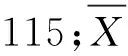
1.2 模型参数的修正方法

Kuz-Ram模型把爆破参数与爆破块度很好地联系起来，具有一定实用的基础，得出的理论计算值和块度分布曲线都有一定的准确性，该模型对于粗粒径部分的预报有较好的准确性，但是用于预报细粒径部分尚有一定的差距。因此对于细粒径料的预测，为了提高预测的准确性，有学者对Kuz-Ram模型的一些参数进行了修正[11]。

(1)岩石系数A的修正

岩体节理、裂隙对爆破的块度分布有很大的影响。岩体本身的性质，如强度、密度、破碎性对于爆破的块度也有关系。岩石系数A就反映这些关系和影响。它是既考虑了岩石的物理学性质，又考虑了岩石节理裂隙发育情况的综合性指标。模型中规定的几种不同情况的取值，并不能全面客观的反映不同岩性、不同节理裂隙开度及分布对岩石破碎块度的影响。C V B Cunningham使用现场反馈的实际资料作了进一步改进，并提出岩石系数A确定的新方法如式(4)～(7)

A=0.06(RMD+JF+RDI+HF)

(4)

RDI=25RD-50

(5)

当E<50 GPa时

HF=E/3

(6)

当E>50 GPa时

HF=UCS/5

(7)

式中：RMD为岩石性能系数；JF为节理特征系数；RDI为密度系数，g/cm3；RD为密度，g/m3；HF为硬度系数；E为杨氏模量，GPa；UCS为抗压强度，MPa。其中岩石性能系数RMD和节理特征系数JF按照文献[11]中规定取值。

(8)

式中各符号含义同上。

2 长九神山灰岩矿爆破块度预测

2.1 工程概况

长九神山灰岩矿是国内规模最大的灰岩矿，矿山位于安徽省池州市西南方向约37 km处。矿区范围面积5.14平方公里。采用露天爆破开采，矿山生产规模为7000万t/a。设计采场采出原矿块度不大于1000 mm。

矿山为独立矿体，相对高差较大，坡角一般为15°～34°，矿区以灰岩为主，夹少量页岩，构造不发育，局部岩溶较发育，岩体完整性较好，硬度3(f系数一般8～12)，密度2.68 g/cm3，湿度在0.27%～1.05%之间，平均值为0.48%，抗压强度在36.3～93.4 MPa之间，平均值为64.9 MPa。除二叠系龙潭组页岩外，岩体稳定性一般。

矿区地质构造复杂，褶皱和断层较发育。矿区内褶皱主要为神山倒转向斜；矿区内断层主要有北西向(F1、F2、F3)断层，其次为近东西向断层(F4、F5)，断层对边坡岩体完整性和稳定性有一定的影响；岩层产状较陡，各分层间无构造破碎带，可溶盐岩主要受节理裂隙的影响，岩体中等完整，呈块状、厚层状，相互间咬合，结构面具一定的粘合力。矿区深部岩溶局部发育。除了具有个别大溶洞外，深部岩溶以小溶洞为主，溶洞发育地段岩层结构承载力降低，可能出现溶洞上层的岩石坍塌或者掉块。

2.2 爆破块度预测

为了验证Kuz-Ram模型在节理发育岩体中预测的准确性，先后在长九神山灰岩矿1#、2#两个采区共进行11次爆破试验，其中1#采区节理裂隙发育，岩性条件较差，共进行了8次试验；2#采区节理裂隙较发育，岩性条件相对较好，共进行了3次试验。爆破试验前典型临空面如图1所示，具体试验参数如表1所示。

图 1 爆破试验前典型临空面Fig. 1 Typical free face before blasting test

表1 神山矿爆破试验参数Table 1 Blasting test parameters of Shenshan mine

根据矿区岩石试验成果及钻孔声波测井完整性评价统计成果，并考虑岩石强度、岩体完整程度及其风化程度等因素，针对矿区石灰岩完整、较完整及破碎三种主要岩体，其岩石力学参数取值大致如表2所示。

表2 长九神山石灰岩主要物理力学参数Table 2 Main physical and mechanical parameters of Changjiu Shenshan limestone

试验区域1#、2#号采区的岩石为较完整岩体，节理、裂隙教发育，其岩石系数计算如表3所示，其中节理特征系数JF取最小值10；现场采用混装多孔粒状硝铵炸药，炸药密度0.8 g/cm3，现场测量炸药爆热约为3700 kJ/kg，爆速约2900 m/s，故在预测模型计算时，炸药相对威力E取值90；石料允许最大粒径取值1 m，结合爆破试验参数，平均预测值如表4所示。

表3 采区岩石系数A计算Table 3 Calculation of rock factor A in mining area

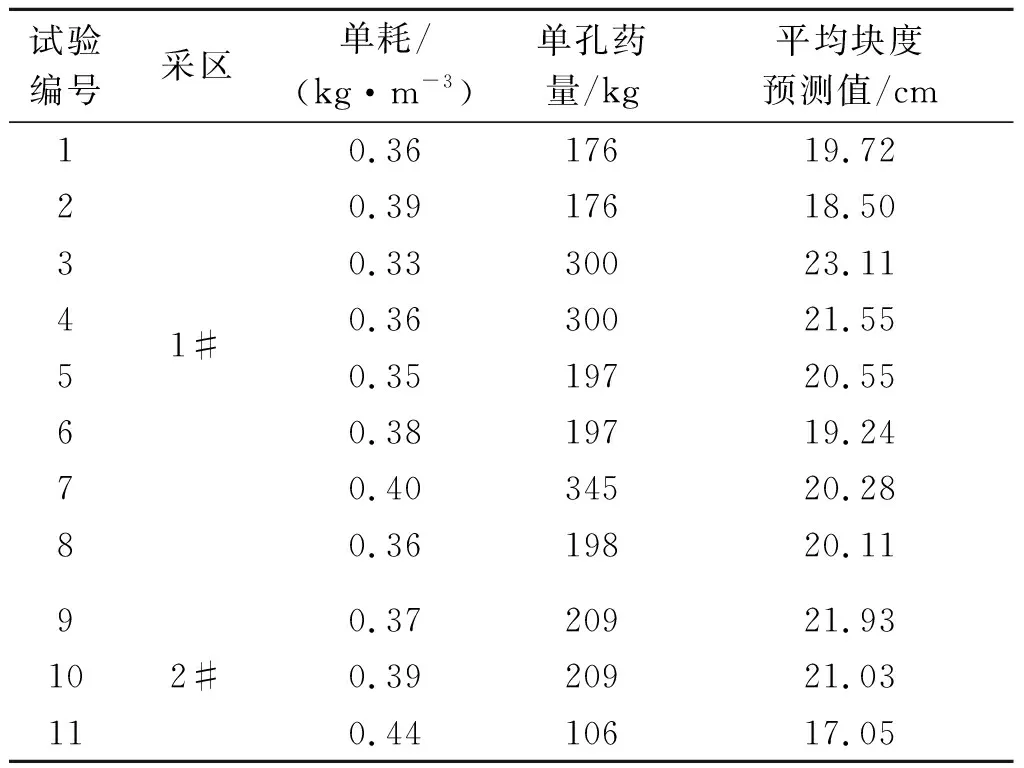
表4 Kuz-Ram模型预测计算表

每一次爆破试验后，选择有代表性的区域进行取样筛分试验，每组爆破试验取样6个点，分别在爆破孔正前方的上部、中部及下部、以及同排两个炮孔中间的上部、中部及下部。取样时，需扒开爆堆表层2～3 m厚的爆渣，取爆堆内部的岩样，每个取样点，取约1 m3样品。爆破试验后典型爆堆如图2所示，典型块度分布如图3所示，现场筛分试验先通过移动筛分机将取样的岩石分为120 mm以上，60～120 mm，60 mm以下三部分，根据筛分规程测量统计120 mm以上粒径岩石的尺寸并对60～120 mm和60 mm以下岩块进行人工筛分，如图4所示。

图 2 爆破试验典型爆堆Fig. 2 Typical explosion pile in blasting test

图 3 爆破试验典型块度分布图Fig. 3 Typical block distribution of blasting test

图 4 现场筛分试验Fig. 4 Field screening test

根据现场筛分试验，可以得到每一次爆破试验后的爆破块度分布曲线以及平均块度的筛分实测值，爆破试验典型爆破块度分布曲线如图5所示，利用Kuz-Ram模型计算得到的平均块度预测值与实际值比较如表5所示。

图 5 典型爆破块度分布曲线Fig. 5 Distribution curve of typical blasting fragmentation

表 5 平均块度预测与实测比较表Table 5 Comparison between average fragmentation prediction and actual measurement

表6 采区修正后岩石系数A计算Table 6 Calculation of corrected rock coefficient A in mining area

3 块度预测模型中岩石系数的修正

3.1 节理特性对岩石系数的影响

在一些地质条件下，使用预测模型对平均块度进行计算时，需要对模型进行修正，通过修正使计算爆破块度分布曲线与实测爆破块度分布曲线更加吻合，这样有利于将通过计算确定的爆破设计参数用于现场布孔装药，取得满足设计级配块度要求的效果。

3.2 岩石系数A的修正

虽然C V B Cunningham结合现场实际资料的反馈对岩石系数A的计算提出了新的方法，但在Kuz-Ram模型实际使用过程中，平均块度的模型计算数值与现场实际筛分值仍存在一定差距，为了优化岩石系数A的取值，现通过长九神山矿料场爆破试验结果对其计算公式进行修正，使其预测结果更具有实际意义。

在岩石系数A的计算中，主要计算参数有岩石性能系数，节理特征系数，密度系数，硬度系数。其中节理特征系数按照表2取值，但在节理发育岩体中，可能存在多组节理裂隙交错出现的情况降低岩石强度，使得爆破后岩体较为破碎，故在取值时可以尽可能取最小值。

岩体内部的裂隙、节理对岩体性质影响最大，但在计算公式中节理系数占比重较小。在实际的岩石爆破过程中，炸药与岩石的波阻抗很难完全匹配，且岩石密度系数在岩石系数占据很大比重，且对于节理裂隙发育程度差异较大的1#、2#两个采区，其密度系数差距很小，从而降低了节理特性在其中的占比，故提出在岩石系数A的计算中，删去密度系数RDI。修正后的岩石系数A计算公式如式(9)

A=0.06(RMD+JF+HF)

(9)

采用修正后的计算方法计算得到的采区岩石系数A如表6所示，结合爆破试验参数，其他参数均不变，仅不考虑岩石密度对爆破块度的影响，使用修正后岩石系数计算得平均预测值与现场实际值比较如表7所示，不考虑岩石密度系数修正岩石系数前后计算值与实际值相对误差对比如图6所示。

表7 平均块度预测与实测比较表Table 7 Comparison between average fragmentation prediction and actual measurement

图 6 修正前后相对误差对比图Fig. 6 Comparison of relative error before and after correction

从图6中可以看出，修正后的模型预测值相对误差比之前未修正公式有显著的减小，误差基本在20%以下，说明Kuz-Ram模型的预测趋势和变化符合客观规律，但是其对于岩性的描述并不是适用于所有的岩性情况，对于节理裂隙发育的岩体，可能存在各种节理裂隙交错出现的情况，通过模型计算得到的岩石系数要比实际情况要大很多。从而使用预测模型计算所得的预测平均块度与实际有较大的差距，影响爆破参数的确定与优化。

3.3 岩石系数A修正的验证

为了验证修正后岩石系数A计算方法的准确性，在长九神山灰岩矿1#、2#两个采区分别进行了两组四次验证性试验，试验参数如表8所示。验证性试验进行场地岩性比之前较好，故节理系数取12，岩石系数A取值如表9所示，四次试验现场筛分后得到的块度曲线如图7所示，利用修正后模型计算得到的计算值与现场实际筛分值对比如表10所示。

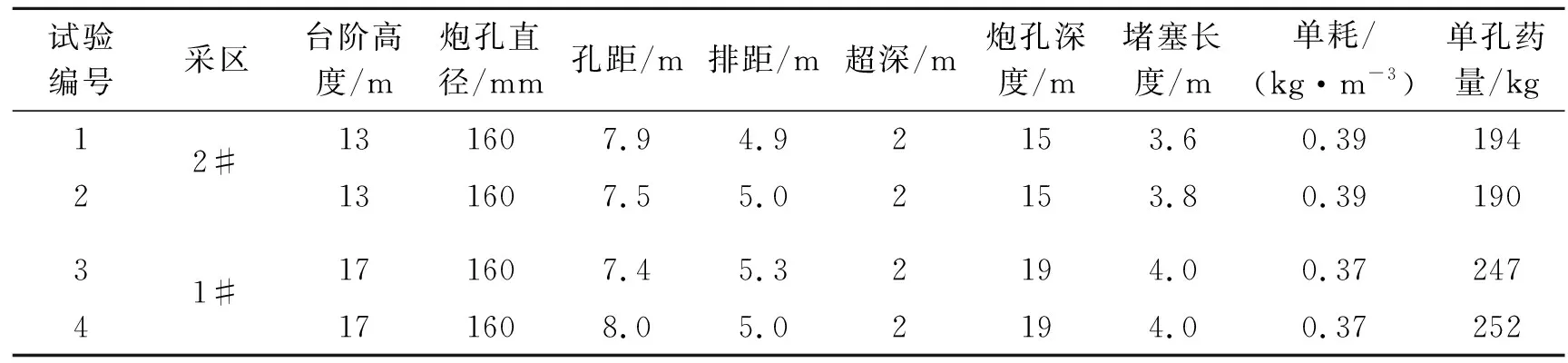
表8 神山矿爆破验证性试验参数Table 8 Verification test parameters of blasting in Shenshan mine

图 7 爆破块度分布曲线Fig. 7 Blasting fragmentation distribution curve

表 9 采区岩石系数A计算Table 9 Calculation of rock factor A in mining area

从表10可以得出，对于4次验证性试验，由于岩体的节理裂隙发育具有的复杂性和不确定性和现场筛分试验过程中可能存在的一些误差，使用修正后的预测模型计算得到的平均块度与实测平均块度仍存在一定的误差；但该误差均在10%以下，属于可接受范围内。修正后的预测模型对于孔网参数的确定与优化具有很大的意义。

表10 平均块度预测与实测比较表Table 10 Comparison between average fragmentation prediction and actual measurement

4 结论

本文结合长九神山灰岩矿区的11次爆破开采试验，对爆破后的爆堆进行人工筛分试验获得爆堆的平均块度，利用爆堆平均块度的实测值，针对长九神山矿区两个采区的岩性对预测模型进行参数优化，并在现场进行4次验证性试验对修正的模型进行验证，得到以下结论：

(1)岩体的节理裂隙对爆破后的块度分布具有很大的影响，Kuz-Ram模型中虽然有对岩石性质的描述，规定了几种情况下的岩石系数的取值方法及计算公式，但是岩体具有复杂性，模型中给出的计算公式并不能客观、全面的反映出岩体中节理、裂隙对爆破后块度分布的影响，所以针对不同的地质条件，需要对模型进行优化。

(2)长九神山灰岩矿料场，岩体节理裂隙发育程度高，通过Kuz-Ram计算得到的平均块度预测值与现场人工筛分实测的平均块度误差较大，最高超过90%。通过Kuz-Ram模型计算的平均块度并不反映实际值，需要对模型的岩石系数A进行优化。

(3)通过对现场爆堆筛分得到的平均块度值，对两个采区的岩石系数A的计算公式进行优化，并通过验证试验检验。使用修正后的模型计算得到的平均块度相较之前计算结果要更接近实际值，说明通过实测平均块度对Kuz-Ram模型进行修正的方法是可行的。

(4)在长九神山灰岩矿后续的实际开采爆破中，建议采用修正后的岩石系数计算方法，即不考虑密度系数的影响。

通过对预测模型进行修正，可以使预测结果更接近实际值，具有参考意义。修正后的模型计算结果与实测值仍存在一定的误差，误差基本小于20%，在可接受范围内。由于在人工筛分的操作过程中可能存在一定的误差，使得优化结果可能存在一定偏差，在后续的研究过程中会加以改进。