基于被动跟踪环境的自适应修正角度滤波算法

刘晓阳，徐炜莉，陈基茗，徐沛然，周祥祥

（1.上海机电工程研究所，上海 201109；2.上海航天技术研究院，上海 201109）

0 引言

近年来，反辐射导弹、隐身飞机和电子对抗等雷达对抗技术迅速发展，以雷达为代表的有源定位系统受到越来越严重的威胁。而相对于雷达等有源定位系统，无源定位系统不辐射电磁信号，它只通过测量目标可见光或红外参数或其发射的电磁信号参数来确定目标的空间位置，具有隐蔽性好、生存能力强等优点［1］。

当前，电子干扰机在朝着多干扰波束方向发展的同时，干扰机在作战过程中对其干扰范围内的雷达进行干扰，使受到干扰的雷达无法测到回波时间，从而得不到距离信息并且失去对其进行定位和跟踪的能力。然而，被干扰的雷达仍然可以获得干扰机的方位和俯仰信息。基于此，在干扰机环境下的目标被动跟踪定位问题也成为了很有吸引力的研究课题［2］。

在上述两种背景中，对于目标定位，使用最多、最广泛的一种方法是三角定位法。如果将传感器和目标均看作三维（或二维）空间的点，那么由方位角、俯仰角可以确定一条源自传感器经过目标的射线。通过多部传感器的多条关联目标信息，利用三角定位法，就可以实现目标（含干扰机）的定位和跟踪。

影响定位结果精度的因素有很多，包括定位模型输入数据的精度、传感器之间的布阵距离、目标与传感器之间的关系等，而其中影响最大的便是定位模型输入数据的精度。为了提高输入数据的精度，需采用滤波的方式对目标跟踪数据进行处理。滤波算法有很多种形式，比较典型的有Kalman滤波［3-4］、α-β滤波、α-β-γ滤波［5-8］、平方根中心差分卡尔曼滤波［9］以及交互多模型算法［10］、可变维度算法［11］、输入估计算法［12］等。这些算法对常规目标都可以取得较好的跟踪效果，但是它们方法复杂、计算量大、实时性差，并且当传感器给不出目标距离时，没有目标完整的球坐标信息就无法转换得到完整的直角坐标信息，利用一般的卡尔曼滤波便无法得到较好的跟踪效果。抛开传感器自身探测精度的高低，无法对两个角度滤波降噪以及无法将两路目标信息进行时间对齐是影响探测精度的重要原因。极坐标下，不能通过简单的前后角度数据相减再除以时间而得到角加速度，因为极坐标下的角度变化要考虑伪加速度。

为此，本文引入了伪加速度，提出一种自适应修正角度滤波算法，一方面可以对无距离的目标信息进行滤波降噪；另一方面，可以得到准确的角加速度，利用外推进行时间对齐，为后续三角定位提供更为准确的输入。与此同时，可以为数据融合提供相应的辅助因素，具有很显著的工程意义。

1 自适应修正角度滤波器

在现代的跟踪系统中，雷达给出的距离、方位、俯仰信息这三者是线性无关的，但转化为直角坐标后的三个分量是耦合相关的，而各种算法的假定测量噪声都是高斯白噪声，因此在直角坐标下滤波本身就会存在模型误差。本文引入伪加速度，在球坐标系下建立了伪加速度修正的目标运动模型及外推方程，一方面解决了目标二维角度滤波效果差的问题，另一方面克服了以往球坐标系下滤波的伪加速度未完全修正的缺陷，避免了耦合误差，提升了滤波精度。

2.1 滤波方程

在方位和俯仰方向上分别进行滤波，通过将上一点计算得到的外推值与当前点的测量值加权相加，得到当前点的滤波值，具体滤波方程为

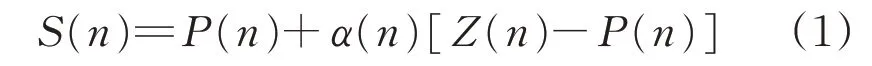
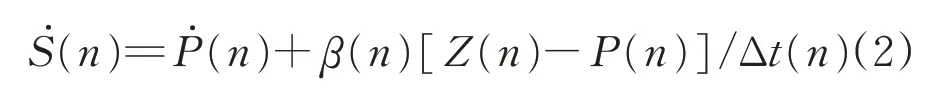
式中：n为雷达观测次数；S(n)代表的参数具体为Al(n)、El(n)，分别表示方位角、俯仰角的滤波值；P(n)代表的参数具体为Aw(n)、Ew(n)，分别表示方位角、俯仰角的外推值；Z(n)代表的参数具体为AZ(n)、EZ(n)，分别表示方位角、俯仰角的测量值；为S(n)的一阶导数；为P(n)的一阶导数；α(n)代表的参数具体为αA(n)、αE(n)，分别表示n时刻方位角A、俯仰角E的滤波器增益；β(n)代表的参数具体为βA(n)、βE(n)，分别表示n时刻方位角A、俯仰角E变化量对应的滤波器增益；Δt(n)为n和n-1次观测时刻的时间差，即雷达采样间隔。

2.2 参数计算

增益的计算式为

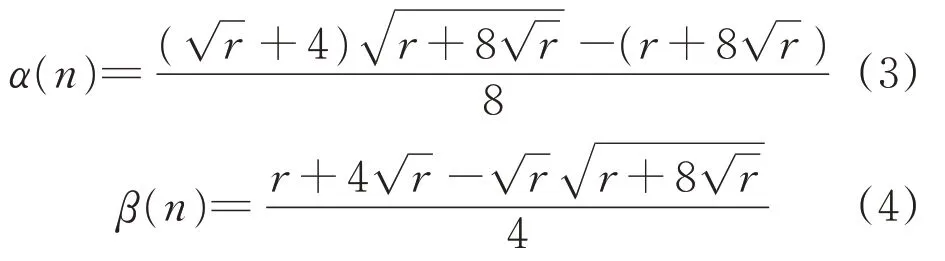
信噪比参数r的计算式［13］为

测量误差通常可取探测装置的精度指标，机动方差可由以下方式获得。

令残差V(n)为

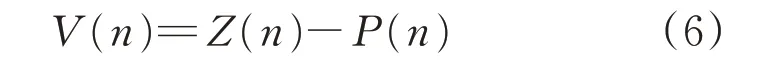
设有N个残差，则其方差为

2.3 数据剔点

数据剔点方法如下：

1） 若 |Az(n)-Aw(n)|≤ΔA且 |Ez(n)-Ew(n)|≤ΔE，则接受本次角度的测量值Az(n)、Ez(n)；否则，用外推值Aw(n)、Ew(n)代替测量值Az(n)、Ez(n)。

2）若t(n)-t(n-1)≤0（其中t(n-1)为上一拍滤波值所对应的输入数据时间），则直接剔除该点数据，不调用滤波器。

3）当连续剔除m（该值可根据目标信息的数据率来做调整设置）个点时，滤波器需要重启，采信当前测量值，保证滤波器不会一直处于剔点状态。

2.4 数据外推

数据外推的表达式为

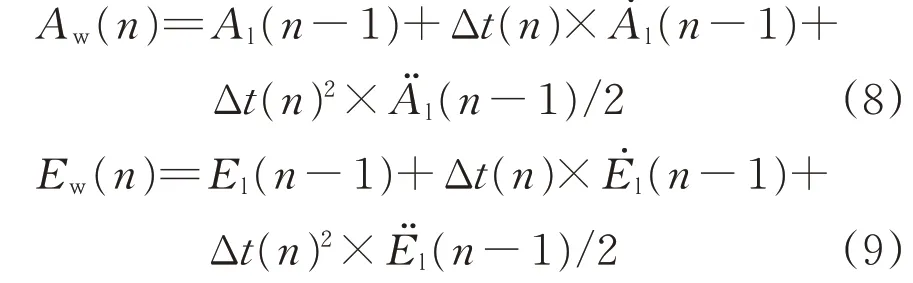
由于目标信息中无距离信息，所以不能将位置转到直角坐标系中进行外推计算。而在极坐标系中，角度的变化可能是非均匀的，所以引入伪加速度，其计算式为

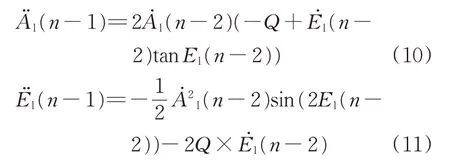
式中：Q为一已知常数，针对不同速度、不同距离的目标，可通过仿真适应性选取该常数值。

方位角角速度和俯仰角角速度则为

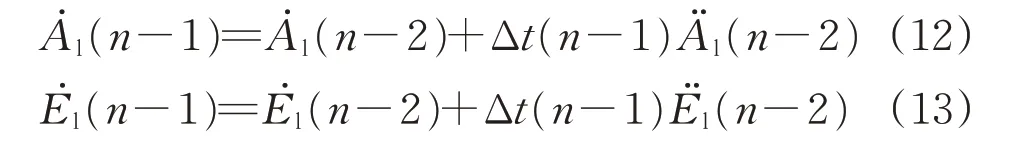
2 算法流程图

在接收目标信息后，对目标的初始速度和最大速度一般会做限幅处理，针对机动目标，也可以适当增大剔点门限或者对目标速度做平滑处理，这里不再详细展开叙述。算法的具体流程参见图1。

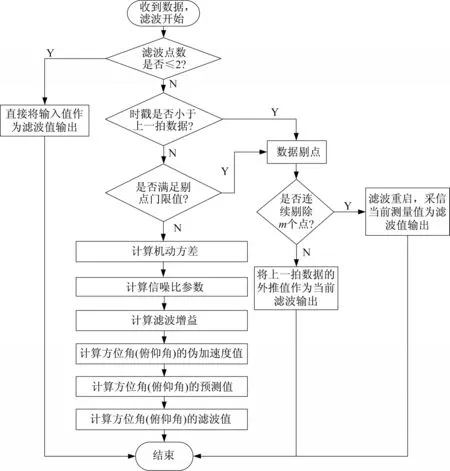
图1 算法流程Fig.1 Algorithm flowchart

3 数值仿真验证

3.1 直线运动目标

利用MATLAB 工具仿真一条目标航迹（带均匀的高斯白噪声），目标进入的X向距离为60 km 左右，高度5 km，航路捷径2 km，目标速度200 m/s，做匀速直线平飞运动。得到理论真值后，构造高斯白噪声，加载到真值上，便可模拟出实际的测量数据。距离上加载的噪声均值为10 m，标准差为10 m；角度上加载的噪声均值为0.3°，标准差为0.3°；常数Q=0.01。

生成目标测量直角坐标系下的目标信息后，将目标位置由直角坐标转成球坐标，将目标的方位角和俯仰角整理成滤波输入文件，发送到滤波器中进行滤波计算，得到角度滤波结果。

下面截取了一段目标信息滤波结果，展示了滤波前后的目标角度信息对比，详见图2～3，验证了本文提出的自适应修正角度滤波算法的确能够在很大程度上减少测量值的噪声。

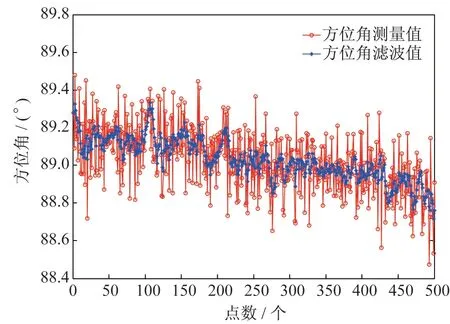
图2 滤波前后方位角信息对比Fig.2 Azimuth information comparison before and after filtering

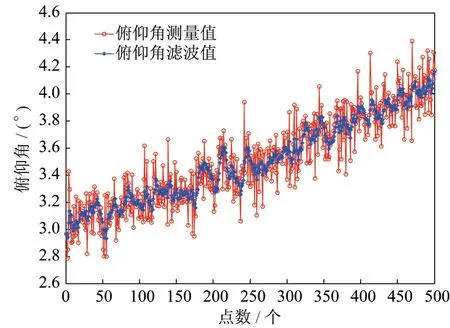
图3 滤波前后俯仰角信息对比Fig.3 Pitch angle information comparison before and after filtering

图4～5 分别对方位角和俯仰角的一次差作曲线图像，对目标整个航迹的滤波结果也做了一个精度统计，详见表1。由表1 的精度统计结果可以得到结论：对于系统误差，一般通过滤波是无法减小的（这与已有认知是一致的），但是角度的起伏误差却得到了很大幅度的降低，验证了本文算法的优越性。

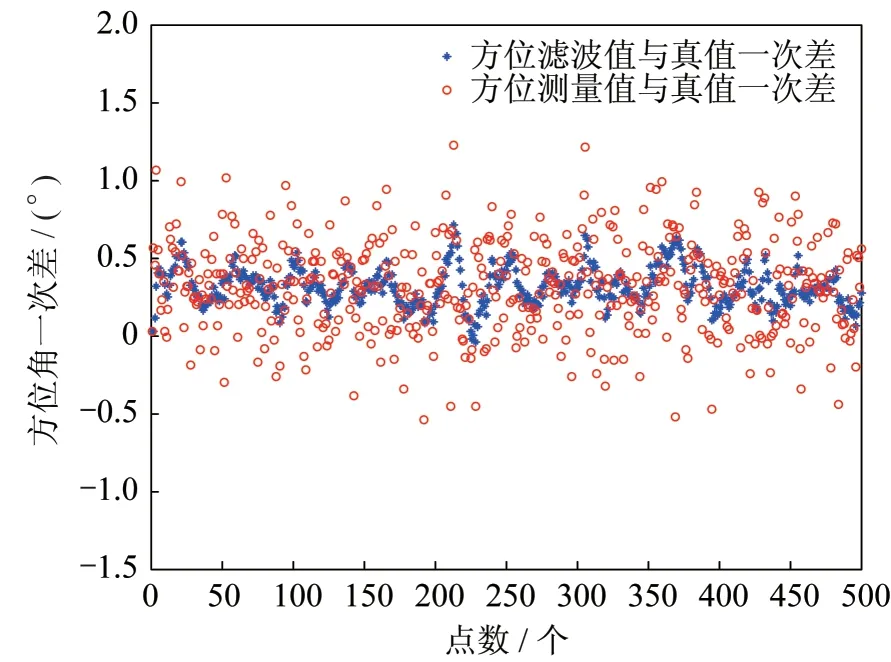
图4 方位角滤波前后结果与真值的一次差对比图Fig.4 The first difference comparison between the truth value and the results before and after azimuth filtering

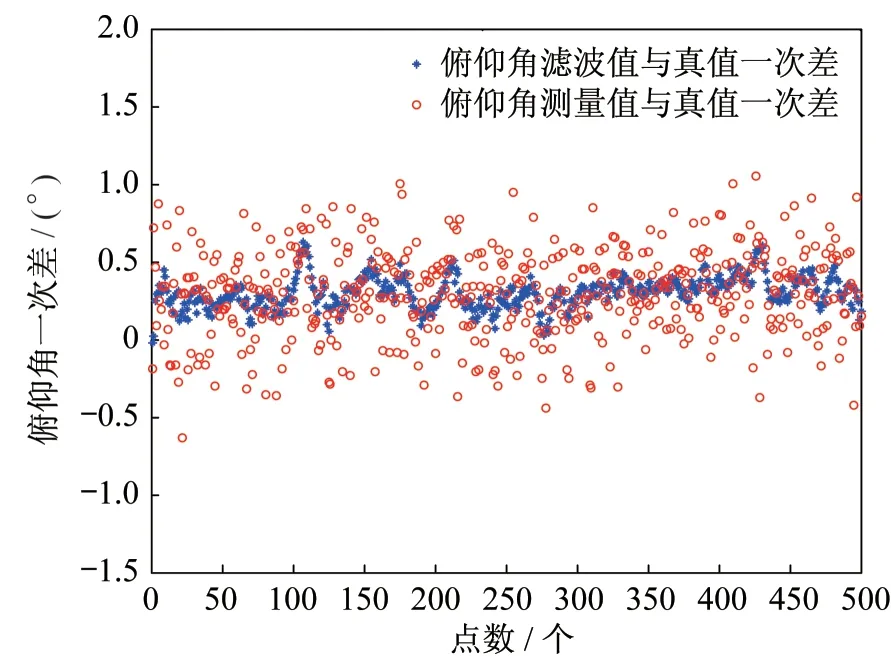
图5 俯仰角滤波前后结果与真值的一次差对比图Fig.5 The first difference comparison between the truth value and the results before and after the pitching angle filtering

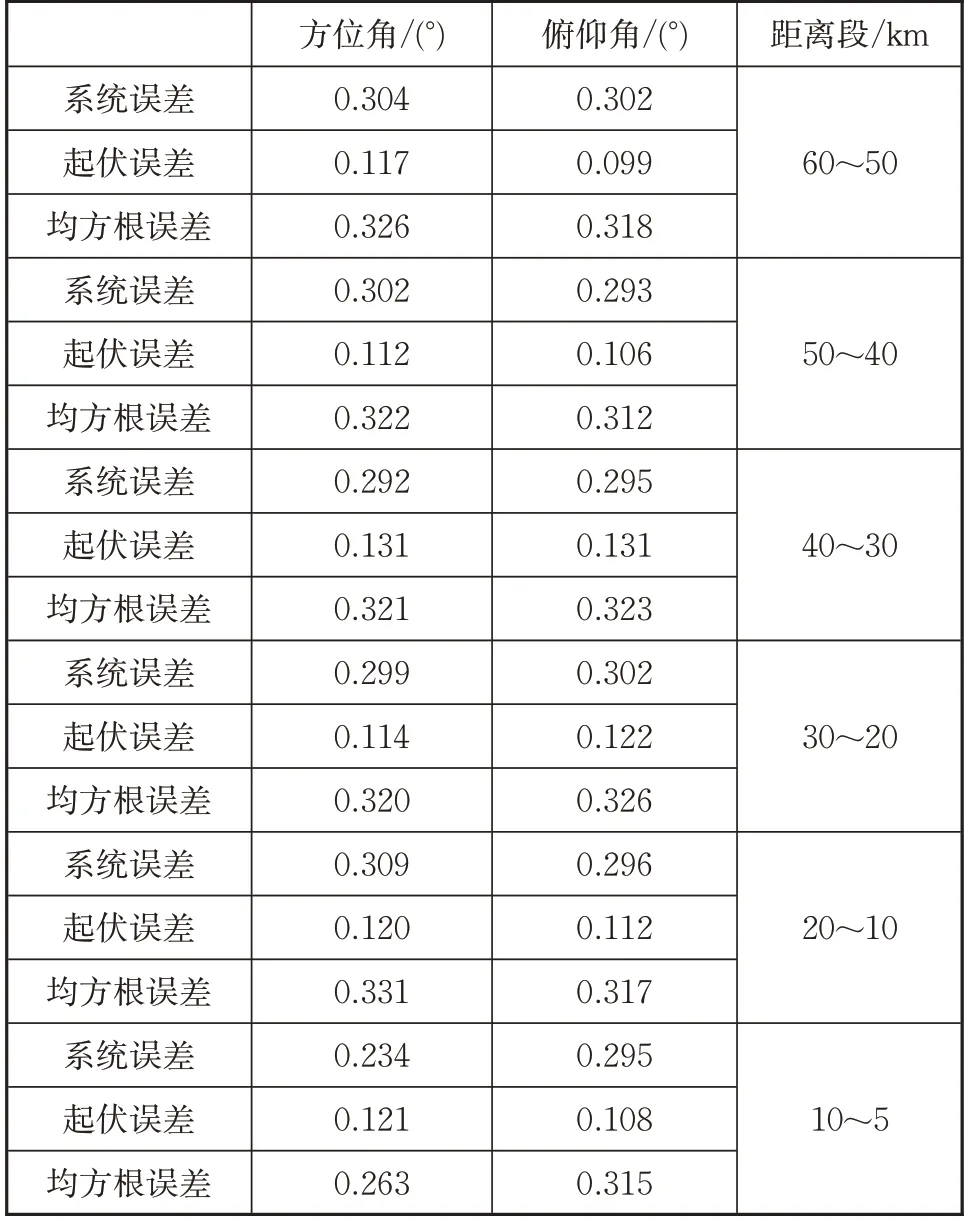
表1 目标数据滤波结果精度统计Tab.1 Accuracy statistics of target data filtering result

3.2 机动目标

目标在水平方向上（X向和Z向）做机动运动，运动航迹见图6。

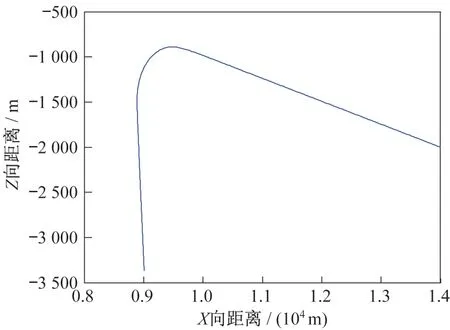
图6 机动目标水平航迹图Fig.6 The track of horizontal movement of maneuvering target

用一般卡尔曼滤波模型对测量数据进行滤波，再用本文提出的自适应修正角度滤波模型进行滤波，得到两种滤波方式下的方位角滤波值，再与目标真实方位角值进行对比，详见图7。再计算两种滤波方式得到的方位角一次差和俯仰角一次差对比情况，详见图8～9。

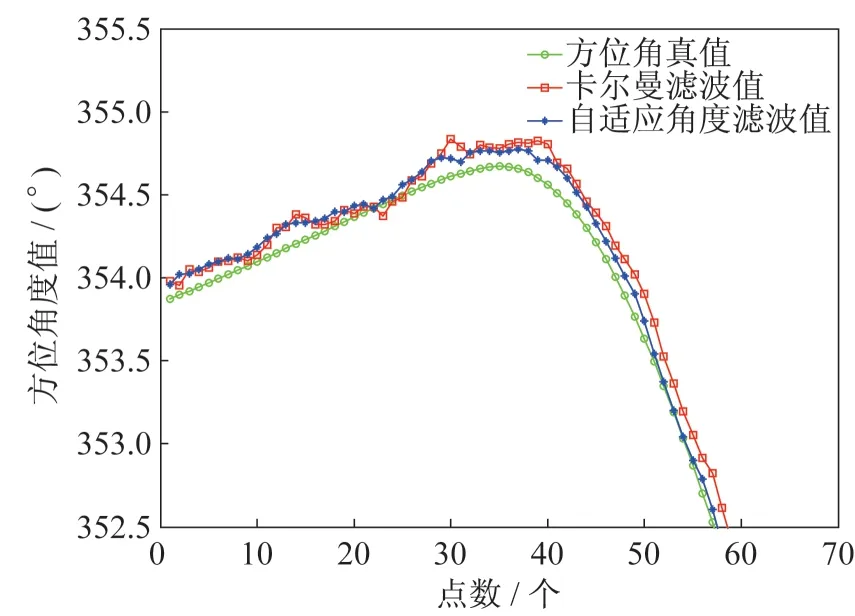
图7 两种滤波得到的方位角与真值对比图Fig.7 The comparison between the true value and azimuth angles obtained by two kinds of filtering

图8 两种滤波得到的方位角值与真值的一次差对比图Fig.8 The first difference comparison between the truth value and the azimuth values obtained by two kinds of filtering

图9 两种滤波得到的俯仰角值与真值的一次差对比图Fig.9 The first difference comparison between truth value and the pitch angle values obtained by two kinds of filtering

从以上对比情况可以看出，一般卡尔曼滤波方法在针对二维数据滤波时，发散情况高于本文提出方法的发散情况，尤其是在滤波起始的一段时间内，发散程度尤为明显；在针对机动目标滤波时，本文提出方法表现出了更好的降噪特性，且在机动后的一段时间，本文方法能够更快地收敛。

综上所述，本文提出的自适应修正角度滤波算法，不但可以表现出极好的降噪特性，同时相较于一般的卡尔曼滤波，表现出更好的稳定性和更快的收敛性。

4 结束语

本文针对被动跟踪和干扰情况下（无法测得目标距离）的目标跟踪数据如何更好地进行滤波降噪进行了分析，提出了一种自适应修正角度滤波算法。该算法考虑了球坐标系下角度伪加速度的影响，建立了伪加速度修正的目标运动外推方程，将机动检测和滤波增益的获取相结合，给出了利用累积残差值来达到自适应获取增益的滤波算法。

通过常规目标数据与机动目标数据、一般卡尔曼滤波算法与自适应修正角度滤波算法的数值仿真对比，验证了该算法的正确性和优越性，解决了只有目标二维数据的情况下滤波效果较差的难题。该算法不但提升了定位模型输入数据的精度，还可以通过伪加速度来求得目标的角速度。一方面为数据融合提供辅助因素，另一方面为多传感器情况下的目标三角定位提供了时间对齐的方法，为提升定位精度奠定了基础。

该算法运算量小，容易满足实时性的要求，具有重要的工程应用价值。