残差卷积注意网络的图像超分辨率重建

谌贵辉，陈 伍，李忠兵，易 欣，刘会康，韩春阳

西南石油大学 电气信息学院，成都610500

在人脸识别、医学成像、卫星图像和视频检测监控等应用领域中，为了取得图像更加丰富的高频信息细节，需要对含噪声模糊不清的低分辨率图像（Low-Resolution，LR）通过一定的处理技术进行处理，得到清晰可靠的高分辨率（High-Resolution，HR）图像[1-3]。最常用的处理方法的是采用图像超分辨率重建技术。超分辨率重建一直是计算机视觉领域的研究热点。

超分辨率重建技术大致分为三类：基于插值[4]的方法、基于重建[5]的方法和基于学习[6]的方法。2014年，Dong等人首次提出了基于卷积神经网络的图像超分辨率重建算法SRCNN[7]（Super Resolution Convolutional Nerual Network）。开启了深度学习应用于图像超分辨率重建。2016年Dong等提出了沙漏型结构的基于快速的卷积神经网络超分辨率重建算法FSRCNN[8]（Accelerating the Super-Resolution Convolutional Neural Network），解决了SRCNN算法中，将低分辨率图像进行上采用的预处理过程，会进一步引入噪声等问题。Kim等人受残差网络结构的启发，通过增加网络层数来加深网络结构，提出了极深卷积神经网络的图像超分辨率算法

VDSR[9]（Accurate Image Super-Resolution Using Very Deep Convolutional Networks），取得了更好的图像重建效果。Shi等人提出了基于亚像素卷积网络的图像超分辨率重建算法ESPCN[10]（Efficient Sub-Pixel Convolutional Network），通过直接在低分辨率图像结构上进行特征提取，然后用亚像素卷积对提取到的特征图像进行上采样，降低了特征提取过程的计算复杂度，提高了重建效率。Ledig等人提出了基于生成对抗网络的图像超分辨率重建算法SRGAN[11]（Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network），通过将生成对抗网络思想应用到超分辨率重建中，结合图像感知损失和对抗损失作为网络的损失函数，使得重建效果更加接近真实高清图像。

VDSR、ESPCN等方法表明：网络深度的加深对超分辨率图像重建质量有至关重要的影响。但训练深度卷积神经网络难以收敛，在训练过程会出现梯度消失和梯度爆炸等问题。同时，未完全考虑到图像全局上下文的信息对提取区域的影响，没有重点关注到图像边缘和纹理等图像细节。对提取的图像特征通道、特征位置和特征空间的信息平等对待，进一步导致重建的图像缺乏全局特征信息。

本文为解决以上问题，在VDSR网络结构的基础上，提出了残差卷积注意网络的图像超分辨率算法。本文中提出的算法主要由低维特征提取结构、多尺度特征融合结构、特征注意提取结构和重建结构这四部分构成。运用多尺度卷积核提取不同尺度的特征信息，并重点关注图像通道域信息进行特征信息的提取。为防止网络过程必要的低频信息的丢失和网络难以收敛等问题，引入短跳跃连接和长跳远连接的残差结构，构建多尺度残差注意特征提取模块，提高图像特征信息的获取精度。同时，本文算法关注图像特征的通道域注意、空间域注意这两种注意力提取的特征信息，引入卷积块注意力模块CBAM[12]（Convolutional Block Attention Module），通过显示建模特征通道间的信息和空间位置注意的相关性，自适应地提取图像特征。网络最后，通过反卷积跳远连接结构进行对重建图像进行恒等映射，进一步提高重建图像质量。实验结果验证了本文算法的有效性，与现有的代表性方法比较，无论是主观视觉评价，还是客观指标评价度量，都表明本文算法的超分辨率重建性能优于其他比较有代表性的方法。

1 相关工作

1.1 多尺度的卷积核

不同尺度卷积核提取的特征信息不同，本文采取1×1、3×3和5×5不同像素尺度的卷积核来对图像进行特征提取。通过多尺度的卷积核对图像进行卷积处理，可以从低分辨率图像中较好地得到更多高频图像细节信息。为节省计算力，不采取尺寸7×7卷积核。受inception结构的影响，将这三种卷积核加宽，来代替传统加深的结构。多尺度卷积核基本结构如图1所示。

图1 多尺度卷积核基本结构

对多尺度卷积核基本结构的输入I L，进行卷积核为1×1、3×3和5×5的卷积操作：

式中，I L表示多尺度卷积核输入的低分辨率图像，H1×1(I L)、H3×3(I L)和H5×5(I L)分别表示使用1×1、3×3和5×5尺寸大小的卷积核对低分辨率图像I L的卷积操作，并经过ReLU激活函数。F1×1、F3×3和F5×5分别表示经过对应卷积核操作和ReLU激活函数后提取到的图像特征图。Hconcate,1×1(I L)表示使用concate函数，将不同尺度卷积核下得到的图像特征图进行特征融合，同时为保证输入和输出的图像特征图的维度保持不变，使用1×1卷积核进行卷积操作，降低特征图维度，减少参数量。

1.2 通道注意力机制

在进行图像卷积的过程中，对所有通道特征进行平等对待处理。为了解决这个问题，He等人在文献[13]中提出的通道注意力CA机制，重新校准先前获得的通道相互依赖的特征，获得信息可以最大限度地利用通道，通过挤压和激励两种操作显式建模通道依赖项的详细信息。

挤压操作中，假设U=[u1,u2,…,u k]是k个空间维数为w×h的不同输入通道。特征压缩首先通过全局平均池化对空间维数进行压缩。空间信息放入通道描述符中，通过使用全局平均池化生成通道统计量。即2D的每个特征通道都变成在某种程度上具有全局接受域的统计量。实际上，Z∈Rk刻画了通道特征并允许输入附近的层来获取全局接受野。通道信息统计量Z∈Rk是通过其空间维数w×h收缩U得到。在挤压操作中，输出维度匹配，输入特征通道的数目。因此统计Z的第c个元素可以定义为：

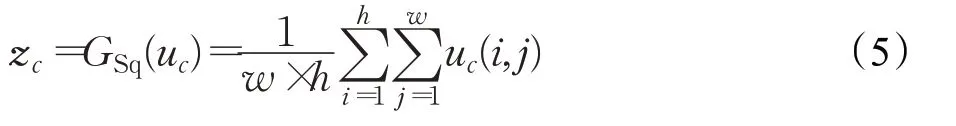
式中，GSq()⋅表示全局平均池化操作，u c(i,j)表示第c个通道特征u c在(i,j)处的值。转换U的输出可以理解为统计描述符的集合，通道信息统计量是整个图像信息的表现形式，采取的聚合方式为全局平均池化操作。

激励操作，利用挤压中聚集的图像信息统计量，接下来进行激励操作。这是一种类似于门结构的机制，在长期短期记忆（LSTM）中提出。这种门机制为每个特征生成通道权重。通道权重为学会显式地建模特征通道之间的相关性，采取sigmoid函数作为门控机制函数。具体定义如下：

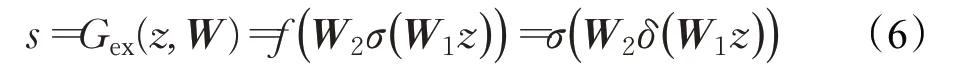
式中，δ表示ReLU激活函数，为了限制模型的复杂性和辅助泛化，通过形成参数化浇注机制。即两层完全连（FC）的瓶颈非线性层，具有减速比r（本文算法中r取16）、ReLU和维度增加层返回到转换的通道维度输出U。减速比r其目的是减少通道的数量然后减少计算力。实际上，整个过程分为四个部分：降维层、ReLU激活、增维层和sigmoid激活层。最后一个sigmoid函数功能是为了生成最终的特征图像信息s，这是该CA机制的核心。CA机制的输出特征通过s重新调整信道，如下所述：最终输出通过使用激活重新缩放U：

式中，U͂=[u͂1,u͂2,…,u͂c]和Fscale(u c,s c)表示的是通道注意力校准的标量s c与原始输入特征图u c∈Rh×w×k之间逐通道相乘。而s表示最终的信道统计量。对于每个通道元素有u͂c=s c⋅u c。通道注意力CA机制示意图如图2所示。

图2 通道注意力CA机制示意图

2 残差卷积注意网络

本文整体神经网络框架如图3所示，残差卷积注意力神经网络由低维特征提取结构、多尺度特征融合结构、特征注意提取结构和重建结构这四部分构成。

图3 残差卷积注意神经网络结构

2.1 低维特征提取结构

在基于残差卷积注意网络的浅层结构中，采用尺寸大小为3×3的卷积核进行网络低维特征的提取，卷积层表示为：

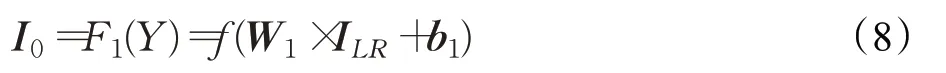
式中，I LR表示原始输入的低分辨率图像，W1表示n个大小为k×k×c的滤波器，偏置项为b1。f表示激活函数，本文采用ReLU激活函数。F1(Y)表示低维特征提取结构得到的n张特征图，I0表示输出特征图。

本文k取3，n取64。不同于以往在亮度通道上进行处理，本文的图像超分辨率重建算法直接在低分辨率的RGB图像上进行操作，避免了忽略其他颜色通道的信息，因此c取3。在每次卷积操作前都对图像边界进行补零padding操作，充分挖掘图像边缘特征信息。

2.2 多尺度特征融合结构

本文提出的多尺度特征融合结构由多尺度残差注意块和多级特征融合层结构组成，可以更好地利用多尺度卷积核提取到不同的特征信息，并经过融合层结构，对提取到的多种图像特征信息进行自适应地融合。经过低维转换层的输出特征I0作为多尺度残差注意块单元结构的输入特征图。经过实验，采取8个多尺度残差注意块，I0输入到8个依次顺序连接的多尺度残差注意块。设计的多尺度残差注意块如图4所示。

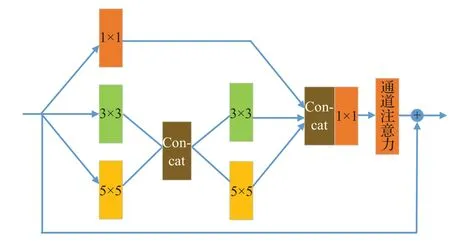
图4 多尺度残差注意力块

多尺度残差注意块对I0进行不同尺度的特征信息提取：

式中，F i是第i个多尺度残差注意块的映射函数，W i是Fi的权重矩阵参数，b i为F i的偏置项矩阵参数，考虑到计算力本身，常常忽略偏置项b i,I i是第i个多尺度残差注意块的输出。

多级特征融合层结构将每一级多尺度残差注意结构的输出特征I i进行并联连接，生成特征信息I M，再通过2个卷积层，卷积核大小为1×1，进行进一步的特征信息融合和降维，对提取到的特征信息最大利用化：

式中，F M是多级特征融和层的映射函数，W M是F M的权重矩阵参数，b M为F M的偏置项矩阵参数。I M是每一级多尺度残差注意块I i并联连接的特征，I G是多级特征融合层的输出特征。

多尺度残差注意块和多级特征融合层的联合的特征信息提取结构，提出的网络模型能够提取到不同深度、不同卷积核尺度和不同通道之间的特征信息。同时，在末端引入通道注意力层，能够捕捉更好的建模全局依赖关系[14]以及降低无关图像域特征信息[15]，更好地学习到通道之间的相互联系。

2.3 特征注意提取结构

注意力机制能够将更多的注意力集中在感兴趣的信息上，对应在图像超分辨率重建中，图像的边缘和纹理等高频信息是更注重的信息。在本文的特征注意提取结构中采用通道注意力和空间注意力模块的联合模块进行特征注意提取，即引入卷积注意模块CBAM[12]来进行图像超分辨率注意力信息的提取。

CBAM[12]的映射由一维通道注意映射M c∈R1×1×C和二维空间注意映射M s∈R1×1×C，图5显示通道注意力的计算原理过程，空间注意力的计算原理，如图6所示。

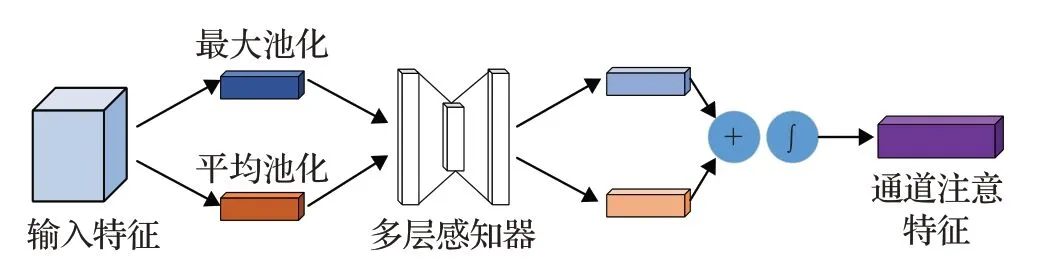
图5 通道注意力计算原理图

图6 空间注意力计算原理图

整个CBAM注意力过程可以表示为如下：

式中，⊗表示逐个元素相乘。在相乘期间，注意力值按顺序进行处理：通道注意力值是在空间维度上处理的，同样地，空间注意力值是在图像通道上进行处理的。F″表示的是最后得到的图像注意力值。图7显示卷积注意模块结构图。

图7 卷积注意模块结构图

2.4 反卷积重建

在神经网络进行卷积操作提取特征信息时，会导致输出的图像越来越小。本文算法在进行上采样的过程中，考虑到这个因素，采取反卷积来进行上采样，能够放大多尺度特征映射图。

采取双三次插值对输入图像做预处理，会引入过多噪声，且会限制学习速度[16]。反卷积进行上采样会减少人工因素的影响。在图像超分辨率重建领域，可以用于图像的放大过程，代替传统的双三次插值操作。本文算法，在进行图像上采样放大过程中，使用反卷积操作进行图像放大，得到想要的图像尺寸大小。

2.5 损失函数

在图像超分辨率重建领域使用最广泛的损失函数是平均绝对误差损失函数L1（MAE）和均方误差损失函数L2（MSE）。L1损失函数具有可以达到较好的主观视觉效果和客观评价指标，可以防止重建图像过于平滑，导致图像失真现象的优点。本文采用平均绝对误差损失函数L1（MAE）来估计网络参数θ。平均绝对误差损失函数表示为：

式中，L(θ)表示平均绝对误差，Y i表示输入低分辨率图像（LR），Xi和F(Y i;θ)分别表示原始高分辨率图像（HR）和重建图像（SR），N代表训练集样本的总数目，网络参数θ为各层权值w i和偏置值b i参数的集合，即θ=(w1,w2,…,w i,b1,b2,…,b i)。通过最小化重建图像与对应原始高分辨率图像的L1损失来估计网络参数θ。为比较L1与L2重建图像的优势，在3.3节对损失函数增加消融实验。

3 实验结果分析

3.1 实验配置

本文提出的算法实验所需要的实验环境为：Ubuntu16.04LTS操作系统，采用深度学习框架Pytorch网络模型进行实验优化，搭建cuda10.0，cudnn7.6.2用于本文算法实验的加速，在进行测试时，使用Matlab R2014a。本文实验硬件设备配置为Intel®CoreTMi5-9600K@3.7 GHz处理器，16 GB运行内存，NVIDIA Geforce GTX2060（6 GB）显卡。

3.1.1 实验数据集

整个实验过程中所使用的数据集，采用的是近年来新提出的一种高清（2K分辨率）的图像数据集DIV2K，其中包含有训练集图像800张，验证集图像100张，测试集图像100张。由于DIV2K仅包含800张训练集图像和100张验证集图像，其100张测试集图像尚未发布，本文采用图像超分辨率领域的基准数据集Set5、Set14和Urban100[17]来进行测试。在进行图像预处理时，采用将DIV2K中的800张训练集图像，分别进行双三次插值下采样2倍、3倍和4倍的降质处理，作为网络的输入低分辨率图像。

3.1.2 实验细节

网络模型中超分辨率网络参数设置，如表1。表中H、W分别是输入图像的高度和宽度，ReLU是线性修正单元，Conv是卷积层，MaxPool是最大池化层，AvgPool是全局平均池化层，ConvT是反卷积层，FC层是全连接层。其中网络模型参数设置：每批16个训练图像对，全部训练图像对共6 720批，作为一个训练周期（epoch），共训练3 000个周期；训练优化算法Adam；初始学习率为10-4；迭代200个周期，学习率减半；卷积滤波器初始化采用MSRA算法；反卷积滤波器采用均值为0、标准差为0.001的高斯分布进行初始化。卷积算子采用的是1×1、3×3和5×5的尺寸。网络层数大体分为14层，包含低维特征提取结构层、多尺度残差注意块层、特征融合层、卷积注意模块层和反卷积重建层等。

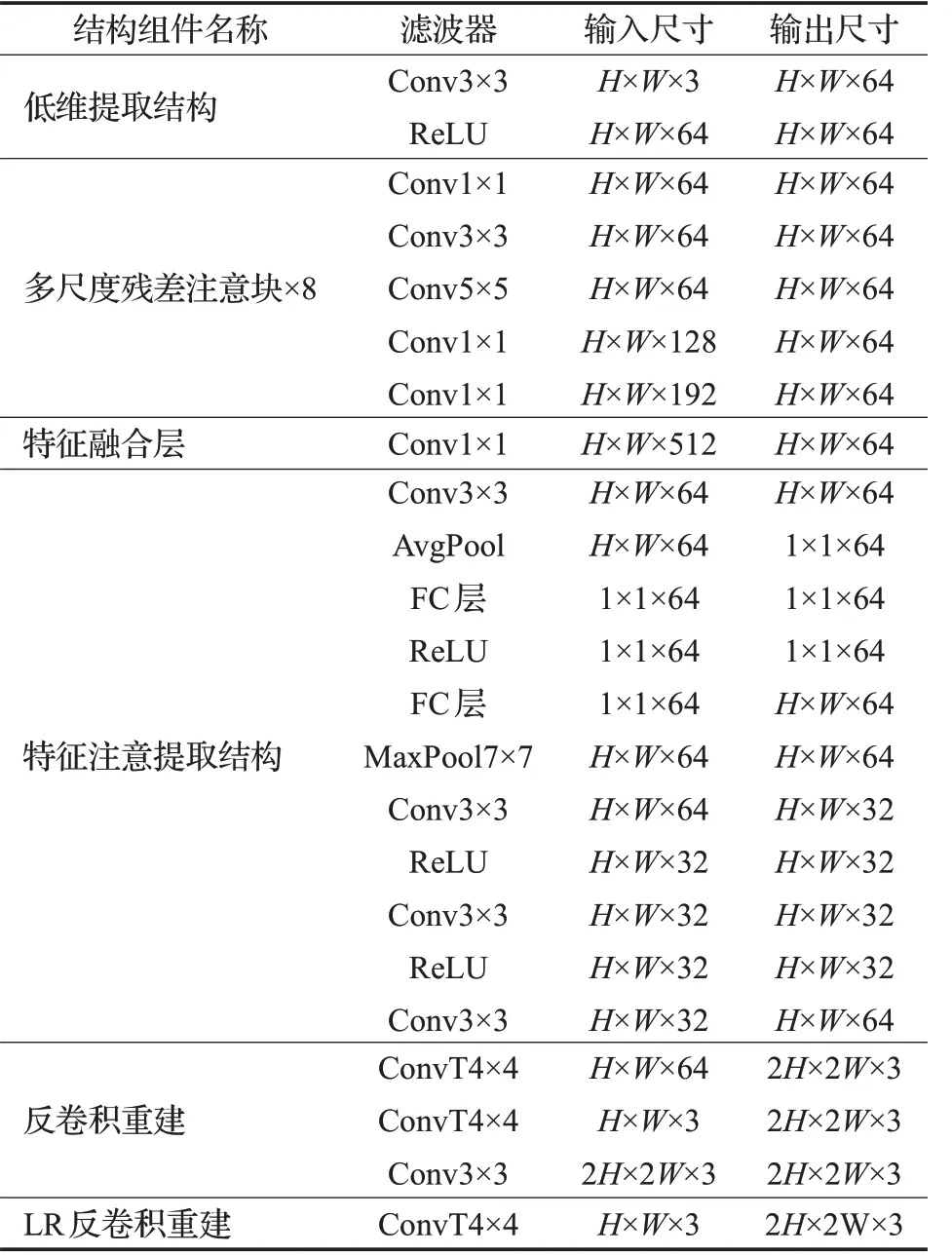
表1 超分辨率网络结构的参数设置

3.2 实验客观评价指标

本文重建图像的重建效果的衡量标准，采用图像超分辨率中常用的客观评价指标：峰值信噪比（PSNR）和图像结构相似性（SSIM）。重建图像的峰值信噪比（PSNR）和结构相似性（SSIM）值在0到1的范围，PSNR是衡量对应像素点间的误差，即误差敏感图像质量评价。

一般情况下，越高的PSNR值表示越好的高分辨率图像，通过均方误差（Mean Square Error，MSE）对峰值信噪比（PSNR）进行定义。

均方误差可表示为：

图像峰值信噪比（PSNR）的计算方法可表示为：

式中，I表示H×W大小的重建图像，K表示H×W大小的原始高分辨率图像，H、W分别表示图像的高度和宽度，n一般取8，表示每个像素的bit数值。峰值信噪比PSNR的单位是dB，PSNR数值越大，重建图像失真越小，重建效果越好。

图像结构相似性（SSIM）的计算表示为：

式中，x表示重建图像，y表示原始高分辨率图像，μx表示x的平均值，μy表示y的平均值，σx表示x的方差，σy表示y的方差，σxy表示x和y的协方差。SSIM取值在[0，1]，越接近1，表明重建图像与原始高分辨率的相似度越高，效果越好。

3.3 消融实验分析

为比较L1与L2重建图像的优势，对多尺度残差注意块数量和损失函数的选择增加消融实验。

对L1、L2损失函数和基础块数量的选择进行算法验证。在L1和L2损失函数下对不同数量的基础块进行实验，并在Set5、Set14和urban100测试集上进行测试，得到了测试集上的平均峰值信噪比。

L1和L2损失函数、多尺度残差注意块的×2超分辨率重建效果在Set5、Set14和Urban100上的平均峰值信噪比，如图8、图9所示。由图知，无论是采用L1损失函数还是L2损失函数，当多尺度残差注意块数量为8时，重建效果最好。

图8 L1损失函数与多尺度残差注意块折线图

图9 L2损失函数与多尺度残差注意块折线图

经过实验验证，当基础块数量为8，选择L1损失函数时，具有最好的重建效果。不同损失函数和基础块设置的网络模型对×2的超分辨率性能的影响，参见表2。

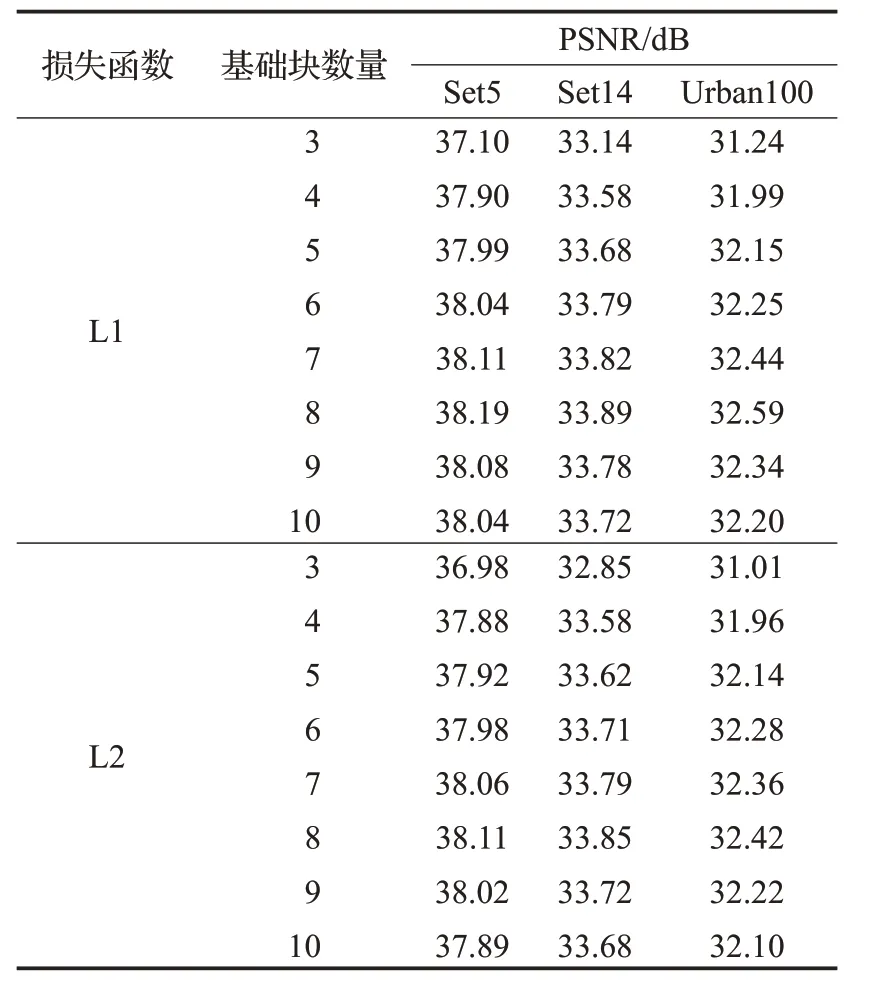
表2 不同变量的网络模型×2超分辨率

从表2中可看出，当使用L1损失函数与多尺度残差注意块数量为8的时候，重建指标最高，而采用L2损失函数和多尺度残差注意块数量为3的基线模型重建指标最差，在Set5测试集的×2尺度中落后于最优配置1.21 dB，在Set14测试集的×2尺度中落后1.04 dB，在Urban100测试集的×2尺度中落后1.58 dB，证明了采用L1损失函数和多尺度残差注意块为8时，提出的重建算法具有最好的重建效果。

采用L1损失函数的重建效果好于L2损失函数，L1具有可以达到较好的重建图像主观视觉效果和客观评价指标，这是L2损失函数所不具有的作用。当多尺度残差注意块数量增加时，重建图像质量越来越高；当注意块数量增加到8时，图像的重建效果最好；当继续增加注意块数量，图像重建质量变低。可能是网络在提取高频图像信息的同时，重建图像所需必要的低频信息被丢弃，使得重建质量变低。这表明当注意块数量为8时，网络具有能够最有效地提取到高频图像信息，同时也保留了必要的重建图像低频信息的能力。

3.4 实验结果分析

为了证明提出方法的先进性与有效性，验证所提出的算法与近年优秀的重建算法的对比效果。选取了单帧图像超分辨率领域先进的五种方法深度学习方法，VDSR[8]、ESPCN[9]、DRCN[18]（Deeply-Recursive Convolutional Network for image super-resolution）和CARN[19]（Accurate，and Light weight Super-Resolution with Cascading Residual Network）和IDN[20]（Fast and accurate single image super-resolution via Information DistillationNetwork）算法与非深度学习图像重建领域传统的Bicubic算法，分别在Set5、Set14和Urban100标准测试集上进行重建图像2倍、3倍和4倍的性能验证实验。结果如表3所示。从表3中可以看出，无论是在2倍、3倍和4倍尺度下，在不同测试集下，提出的算法重建图像的PSNR与SSIM指标均高于这几种算法。上采样因子为4时，在Set5测试集上，本文算法的PSNR值比VDSR提高了1 dB，比CARN提高了0.22 dB。在Set14测试集上，本文算法比VDSR提高了0.75 dB，比CARN提高了0.17 dB。在Urban100测试集上，本文算法比VDSR提高了1.24 dB，比CARN提高了0.35 dB。

表3 不同测试数据集上的PSNR（dB）、SSIM指标对比结果

对不同先进算法的主观视觉效果进行了对比评价，所采用的对比方法的实现均来自作者公开的源代码，使用原论文中的参数和预训练模型得到。图10表示Set5测试集上本文超分辨率重建算法和其他算法的对比，本文算法中的蝴蝶图像放大后，可以更加清楚地观察到纹理细节。图11表示Set14测试集上和其他算法的对比，Set14中的猴子图像从放大眼睛及其边缘的细节可以看出，本文重建算法的猴子眼角纹理和眼睛瞳孔细节对比其他算法均更加清晰。图12表示Urban100测试集上和其他算法的对比，Urban100中栏杆在放大栏杆的细节后可以看出，本文重建算法的高频细节与其他算法重建的图像对比更加清晰，恢复出了主栏杆的细节信息，更接近原始高清图像。因此，提出残差卷积注意网络的图像超分辨率重建效果从视觉效果来看有所提高。本文在极深卷积神经网络超分辨率重建算法的基础上，改进的残差卷积注意网络的图像超分辨率重建算法，在测试数据集上明显优于目前主流算法。甚至优于2018年在ECCV会议收录的CARN算法和2018年CVPR会议收录的IDN算法。

图10 Set5测试数据集上的对比结果

图11 Set14测试数据集上的对比结果

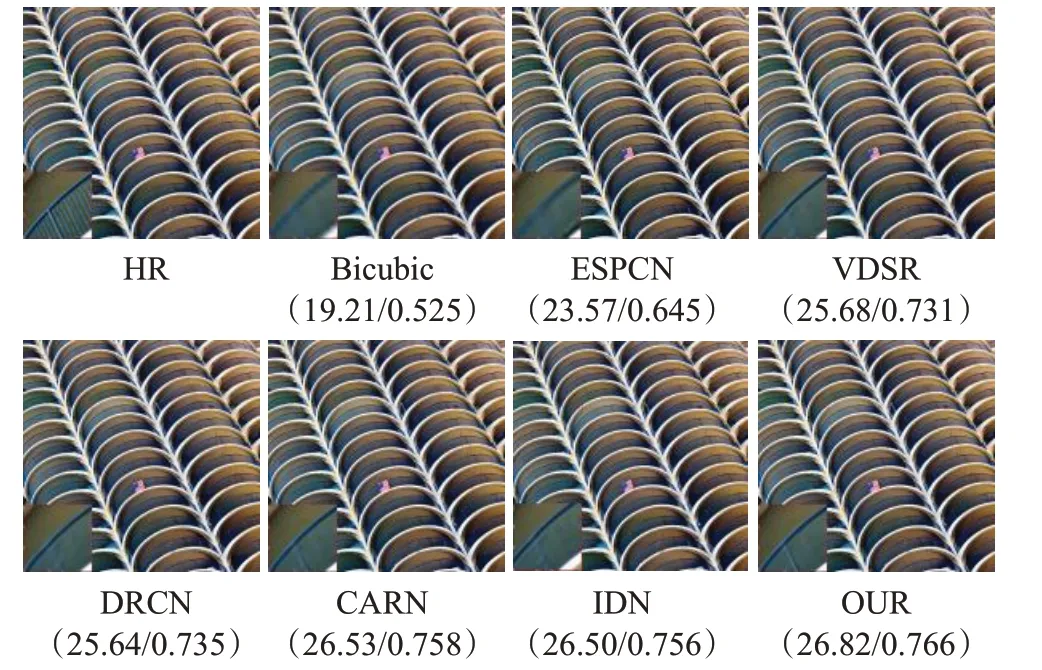
图12 Urban100测试数据集上的对比结果

4 结论

先前基于深度学习的图像超分辨率重建方法中，存在特征提取少、信息利用率低和平等处理图像各个通道的问题。本文受极深卷积神经网络超分辨率重建算法（VDSR）启发，结合卷积注意模块，提出了残差卷积注意网络的超分辨率重建方法。在网络中采取残差注意块局部残差和网络全局残差相结合的方式来降低网络训练难度，取消双三次插值，在最后增加反卷积层，在网络结构中加入concate层进行多尺度特征融合、通过1×1的卷积核进行降维和扩维。构造多尺度残差注意块来学习高分辨率和低分辨率图像之间的映射关系。本文提出的算法能够更好地恢复重建图像的高频纹理图像信息。无论从客观评价指标，还是主观视觉上，均优于目前的主流方法。