一类时滞异质网络的拟同步控制

赵曼宇，叶 军

南京邮电大学 理学院，南京210023

近10年来，复杂网络由于其应用广泛而受到人们极大关注[1-2]。如通信网络、电力系统网络、万维网、神经网络等都可以用复杂网络模型来表示。在复杂网络动态行为研究中，同步性是多个学科的研究重点。到目前为止网络同步的研究已经提出多种同步模式，如指数同步[3]、完全同步[4]、簇同步[5]、有限时间同步[6]、拟同步[7]等。

在研究复杂网络同步问题中，由于网络的复杂性，仅依赖网络自身的耦合实现同步是很困难的，因此为了实现同步提出了多种控制方法。如自适应控制[8]、脉冲控制[9]、牵制控制[10]、采样控制[11]等。随着数字电路技术和计算机网络技术的迅速发展，数字设备逐渐取代实际工业系统中的连续时间设备。因此，采样控制由于其离散性、减少信号传输、降低通信成本等特点被广泛应用于实际系统中。在许多实际系统和信息网络中，时滞现象是不可避免的且会随时间发生变化，而时滞的存在会导致系统不稳定，性能下降，因此对时滞现象的研究具有重要意义。有大量文献研究了含时滞的复杂网络同步问题。

文献[12]研究了具有恒定时滞的复杂网络在非周期采样控制下实现指数同步的问题。文献[13]研究了一类具有通信时滞的复杂网络在记忆采样控制下实现扩展耗散同步的问题。文献[14]研究了具有时变耦合时滞的复杂网络在含恒定信号传输时滞的采样控制下实现指数同步的问题。通过构造含有更多时滞信息以及采样间隔信息的增广Lyapunov-Krasovskii泛函获得了保证系统同步的稳定性判据。文献[15]研究了具有变时滞和扰动的不确定性模糊系统在记忆采样控制下的鲁棒H∞稳定性问题。

含时滞的网络同步问题的研究已经取得了很多进展，但大多数研究都是关于同质系统，即所有节点都具有相同的动力学系统。然而在实际系统中，由于外部干扰、系统突变、参数不确定性和个体差异等因素可能会导致网络系统的异质性。因此对节点动力学不同的异质网络的研究具有重要意义。近年来，异质网络发展迅速。文献[16]研究了基于输入饱和采样控制下异质网络实现拟同步的问题。文献[17]研究了异质二阶多智能体系统在具有输入时滞以及无输入时滞采样控制下实现Leader-following拟一致性的问题。文献[18]研究了在具有脉冲控制的DOS攻击下，异质非线性多智能体系统实现拟同步的问题。文献[19]研究了具有时变通信的连续时间广义马尔可夫切换异质网络的拟同步问题。

综合以上文献，本文拟考虑同时含有时变时滞、输入时滞、异质等因素的非线性复杂网络。研究内容包括：建立含时变时滞的异质非线性复杂网络模型，设计含输入时滞的采样控制协议，利用Lyapunov稳定性理论及线性矩阵不等式方法给出系统实现拟同步的充分条件，并推广了同质的情况。

1 预备知识和模型描述

1.1 符号说明

Rn和Rn×n分别表示n维实列向量的集合和n维实矩阵的集合；I n∈Rn×n表示n×n的单位矩阵；AT表示矩阵A的转置；‖⋅‖是定义为的欧式范数；diag{…}表示对角矩阵；A＞0表示矩阵A是正定矩阵；λmax(A)和λmin(A)分别表示矩阵A的最大和最小特征值；∗在对称矩阵中指的是对称元素；⊗指的是克罗内克积。

1.2 引理

引理1[20]对于任意矩阵，标量τ＞0(0≤τ(t)≤τ),以 及 可 导 函 数x(s)有，其中

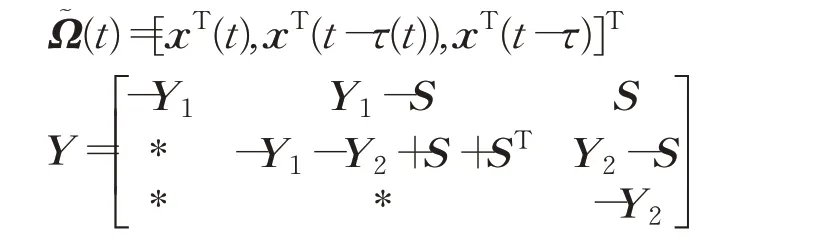
引理2[21]设z∈W[a,b)且z(a)=0，对于任意的n×n维矩阵R＞0，有下面不等式成立：

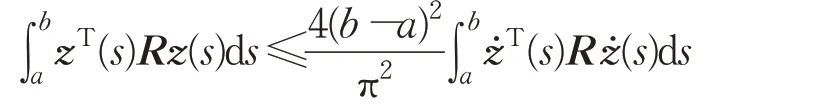
引理3[22]二次函数f(x)=a2x2+a1x+a0其中a2,a1,a0∈R，∀x∈[0,h]，如果（1）f(0)＜0，（2）f(h)＜0，（3）-h2a2+f(0)＜0成立，则f(x)＜0。

注1根据文献[22]中的证明可知，当a2＜0时，由条件（2）和（3）就可以保证f(x)＜0，∀x∈[0,h]。

1.3 模型描述

本文研究由N个跟随者和一个领导者构成的含时变时滞的非线性异质复杂网络，N个跟随者的动力学模型如下：

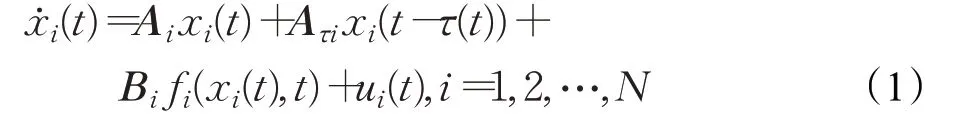
其中，x i(t)∈Rn是第i个节点的状态变量；f i:Rn×[0,+∞)→Rn是第i个节点的非线性向量函数；A i∈Rn×n,Aτi∈Rn×n,和B i∈Rn×n是常数矩阵；τ(t)是时变时滞且满足0≤τ(t)≤τ，τ̇(t)≤u，其中τ＞0，u是常数；u i(t)∈Rn是待设计的控制协议。

领导者的动力学模型如下：

其中，A0∈Rn×n，Aτ0∈Rn×n，B0∈Rn×n是常数矩阵，x0(0)∈Rn是领导者的状态初值。

1.4 定义与假设

假设1每个跟随者与领导者之间至少存在一条有向路径。

定义1非线性函数f(⋅):Rn→Rn满足利普希茨条件：存在αij≥0(i,j=1,2,…,n),∀y,z∈Rn使

假设2设f i(x i(t),t)=f(xi(t),t)+g i(x i(t),t),i=1,2,…,N，其中

（1）f(x i(t),t)满足利普希茨条件；

（2）‖g i(x i(t),t)‖≤σi,σi是正常数。

假设3领导者的状态向量x0(t)是有界的，即存在δ＞0，使得‖x0(t)‖≤δ对任意的初值x0(0)都成立。

注2假设1是网络系统实现领导者-跟随者同步的必要条件，假设1表明领导者可以通过有向路径把信息传递给每一个跟随者；假设2表明系统中的非线性函数满足利普希茨条件，这在非线性系统中是常见的；在实际应用中，领导者可能是一个平衡点、周期轨道或者混沌吸引子。因此，假设3是合理的。

本文设计的采样反馈控制如下：

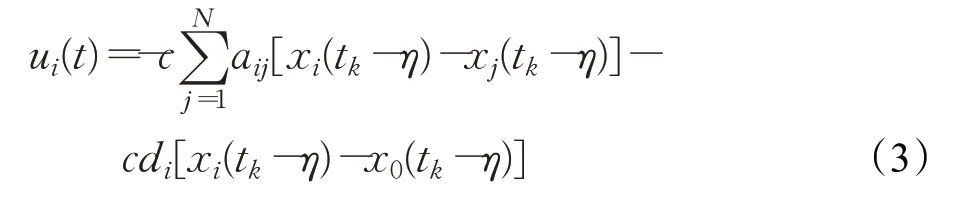
根据图理论知识可知，式中A=[aij]∈RN×N指的是加权邻接矩阵，如果节点i可以收到节点j的信息，那么aij＞0否则a ij=0。拉普拉斯矩阵L=l ij∈Rn×n定义为：当i≠j时，。领导者的判断矩阵定义如下：D=diag{d1,d2,…,d N}∈RN×N，当且仅当第i个节点与领导者相连时d i＞0，否则d i=0。令Hˉ=L+D，式中采样时刻t k满足0=t0＜t1＜…＜t k＜…考虑的采样是非周期的，任意两个连续采样时间间隔在一个区间内，即t k+1-t k=h k≤h，h k＞0是采样间隔，h是允许的最大采样间隔，c为恒定耦合强度，η为恒定输入时滞。

1.5 误差系统

定义误差向量x͂i(t)=x i(t)-x0(t)

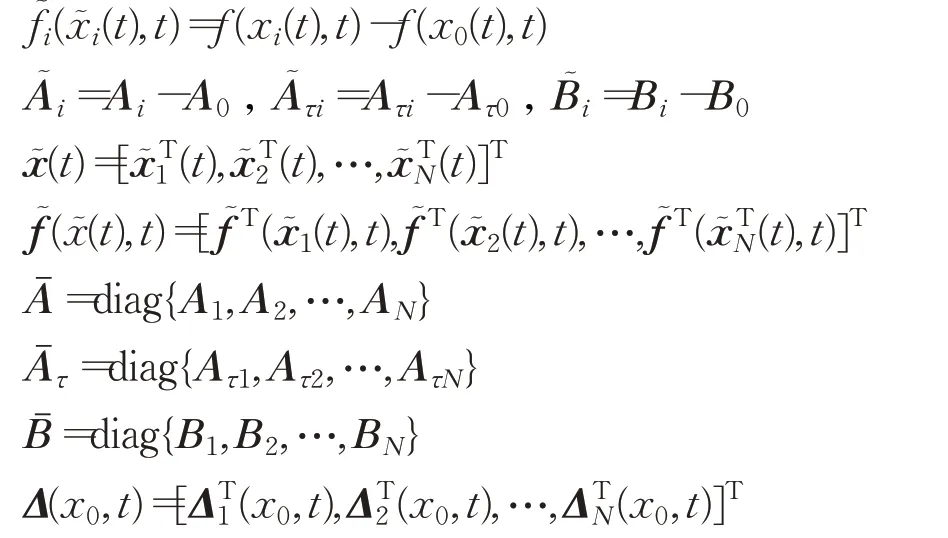
因此误差系统为：

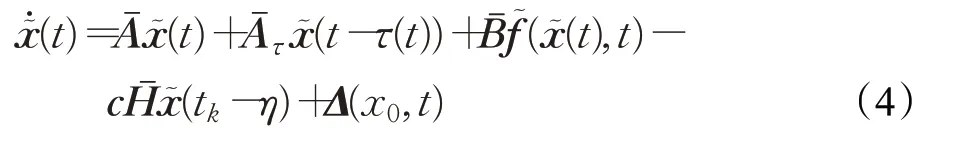
式中

通过文献[16-19]对异质网络的研究发现异质网络很难实现完全同步。因此，引入拟同步的定义如下：

定义2[16]跟随者网络（1）与领导者网络（2）实现拟同步的条件为：存在一个误差界ε＞0，对于任意的初值x i(0),x0(0)∈Rn使得成立。

由于节点的异质性严重影响系统的稳定，当前的一个主要问题是如何处理由异质引起的不稳定因素，从以上分析可以看出Δ(x0,t)的存在正是导致跟随者和领导者之间不稳定的因素，因此有必要估计‖Δi(x0,t)‖的界。由假设2和假设3可得：

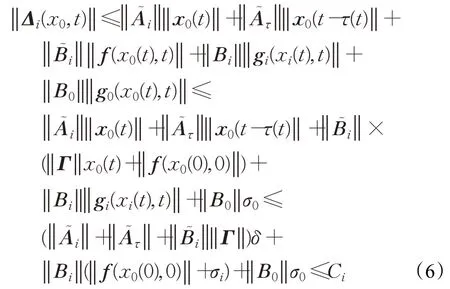
其中Γ=[αij]n×n,i=1,2,…,N。

2 主要结果

本章将给出异质跟随者网络（1）与领导者网络（2）在采样控制（3）下实现拟同步的充分条件。为了简化矩阵和向量的表示，将e i∈R9n×n,i=1,2,…,9,定义为块输入矩阵（如：e5=[0 0 0 0I0 0 0 0 ]T）其他符号定义如下：

定理在假设1～3的基础上，给定正常数h,τ,u,σ1,σ2,α,如果存在矩阵P＞0,X1＞0,W i＞0 (i=1,2,…,6)，矩阵T,N,Z=diag{Z1,Z2,…,Z N}，对角正定矩阵Θ和对角实矩阵Λ=diag{b i}N＞0，使得下列线性矩阵不等式对于任意的hk∈{0,h}成立：

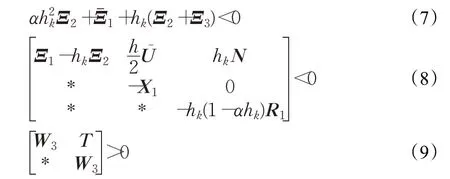
那么，跟随者网络（1）与领导者网络（2）在采样控制协议（3）下可以实现拟同步，同步误差上界为ε=

证明构造下面的增广李雅普诺夫泛函

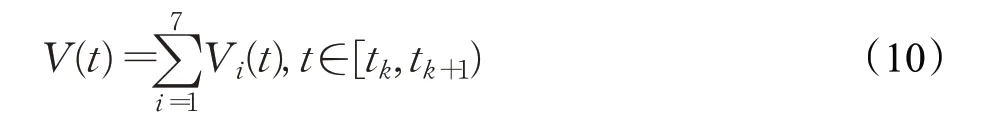
其中

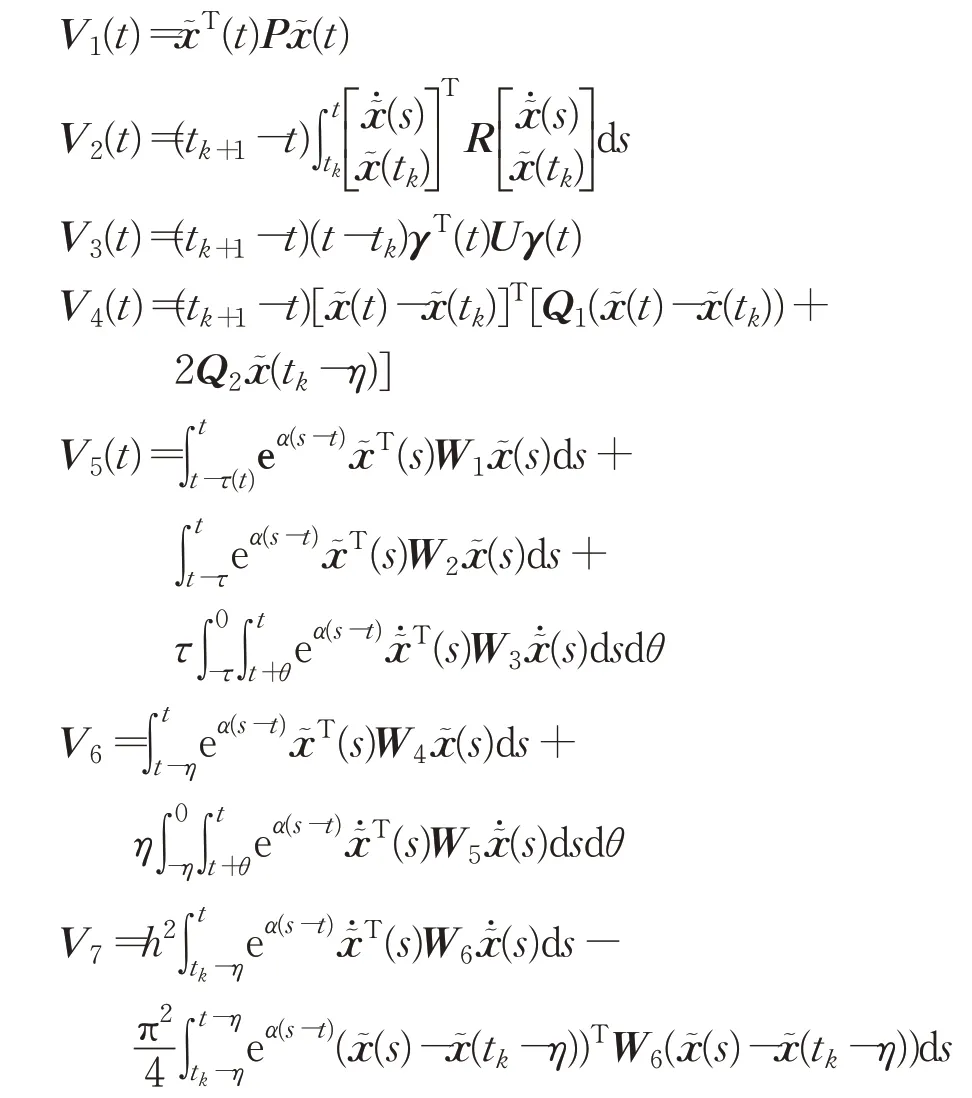
对V(t)沿误差式（4）对t求导：

给定任意的正定矩阵X1有下面不等式成立：

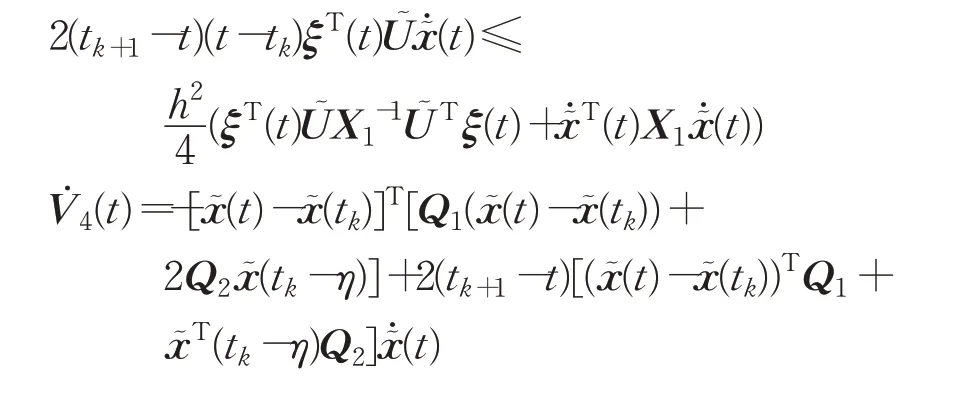
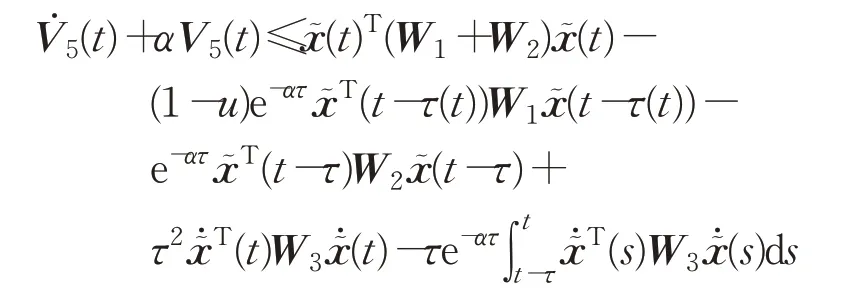
根据引理1可得：

式中

为了证明拟同步需要求得下面式子：

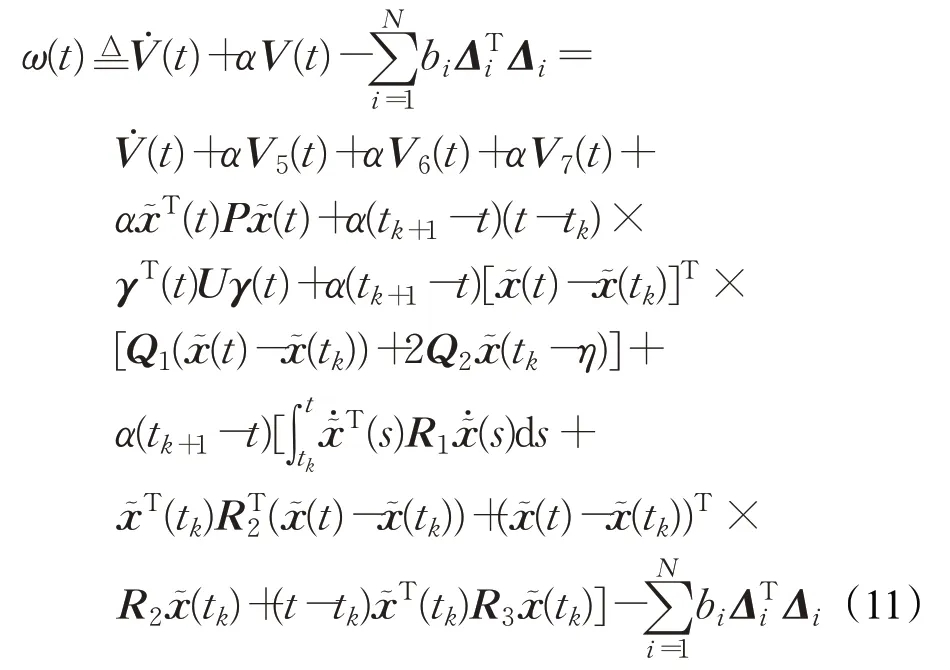
引入下面的不等式来处理和上式中的一部分积分项

应用上式及詹森不等式有下面式子成立：

由定义1和假设2可知，f(x i(t),t)满足利普希茨条件，因此

其中Γ=[αij]n×n

给定一个对角正定矩阵Θ有下面式子成立：

给定一个对角矩阵Z和标量σ1＞0，σ2＞0可得：

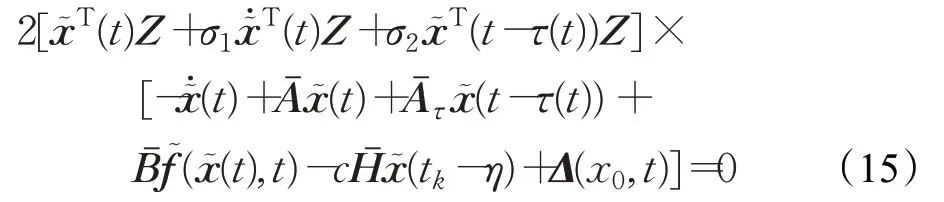
把式（12）、（14）、（15）代入到式（11）中得：

其中：

根据引理3可得Ξ＜0的条件是下面两个式子成立：

根据Schur引理可知定理中的式（8）等价于式（17）。因此，当t∈[t k,t k+1)时：

把式（18）两边乘eα(t-t0)从t0到t可得：

从V(t)的定义可知x͂T(t)Px͂(t)≤V(t)

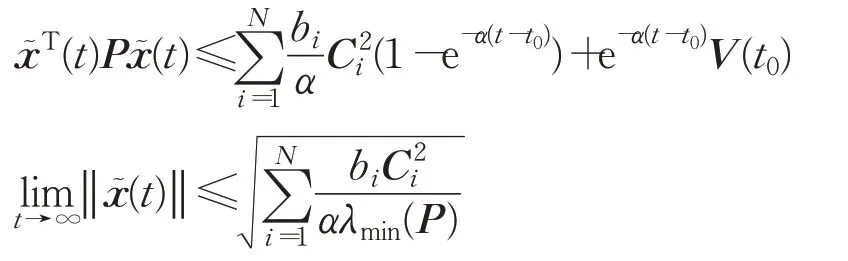
因此，含时变时滞的异质跟随者网络（1）在采样控制协议（3）下可以与领导者网络（2）实现拟同步，且同步误差上界为：

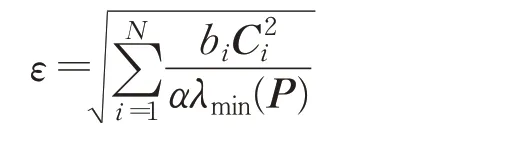
证明结束。

推论假设定理中的条件不变，当t→∞，Δ(x0(t),t)→0，异质网络（1）转变为同质网络，其与领导者网络（2）在采样控制（3）下可以实现完全同步。

3 数值仿真

本章将给出数值仿真来验证理论结果。本文选取的网络包含1个领导者和6个跟随者，领导者作为根节点，节点间的信息交流如图1所示。

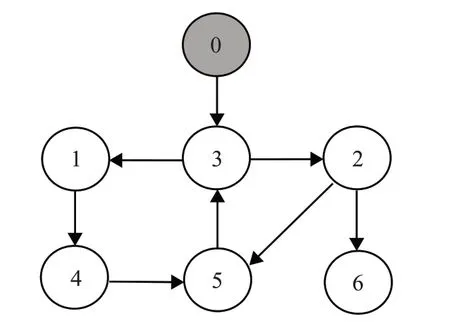
图1 网络拓扑结构图

例1跟随者网络模型为：

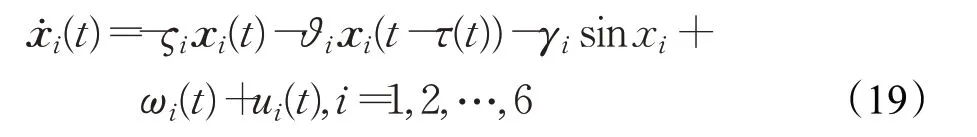
其中，ςi和ϑi是采样常数，γi是模型参数，ωi是输入扰动。因此系统（1）中相对应的参数为A i=-ςi,Aτi=-ϑi,B i=-γi,f(x i(t),t)=sinx i,g i=-γi-1ωi(t)。假 设γi=0.01i,ςi=8-i，ϑi=2+i，[ω1,ω2,ω3]T=[-cos(-2t)+0.2,-sin(-6t),-e-4t,-sin(-2t),-e-2t+0.6,-cos(-8t)]T领导者节点的相关参数为A0=-4，Aτ0=-7，B0=-0.03，g0=-13 cos(-4t)+6。选取耦合强度c=0.5。为了考虑时变时滞以及输入时滞对系统的影响，取τ(t)=0.012 5+0.012 5 sin(4t),τ=0.025,u=0.05,η=0.005。参数α=30,b1=1,b2=2,b3=3,b4=3.5,b5=2.5,b6=1.5,σ1=15,σ2=5,Γ=1。根据网络拓扑图1可知：

通过定理解线性矩阵不等式（7）～（9）得到可允许的h的最大值为0.033。为了简化把控制协议（3）设计为周期采样，采样周期为h k=0.01，同时基于定理可得：

选择领导者的初值x0(0)=1，6个跟随者的初值随机选择。根据以上给定的相关参数以及式（6），通过简单地计算可得C1=8.038 4，C2=6.236 8，C3=4.235 2，C4=2.243 7，C5=1.672 1，C6=4.290 5，进而得到估计误差上界ε=5.4。从图2和图3可以看出含时变时滞的异质跟随者网络（1）和领导者网络（2）在含输入时滞的采样控制（3）下可以实现拟同步。

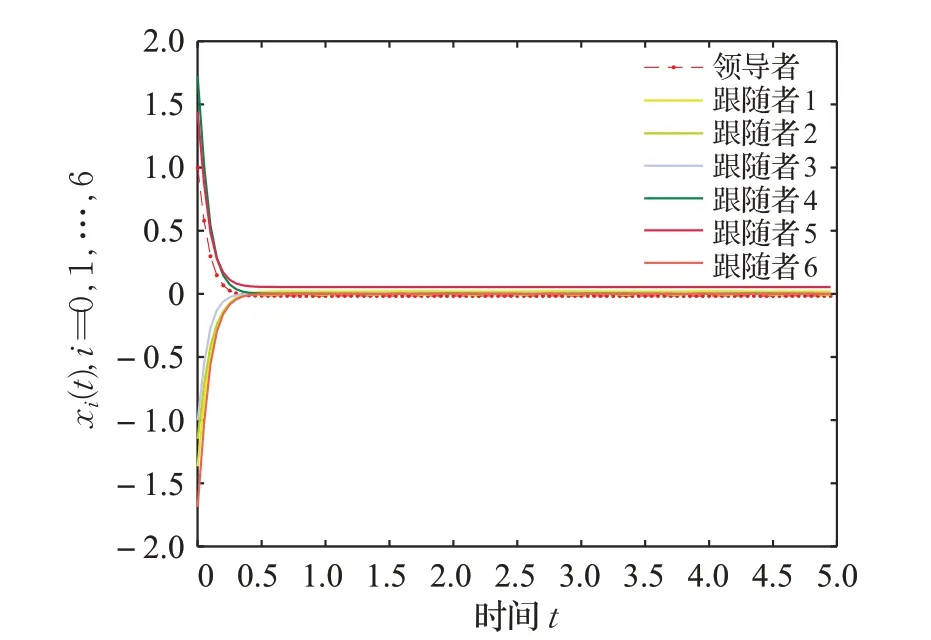
图2 例1中x 0(t)和x1(t),x 2(t),…,x6(t)的轨迹图

图3 例1中实际与估计同步误差图

例2当Δ(x0,t)→0时，异质网络转变为同质网络。同质跟随者网络的模型如下：

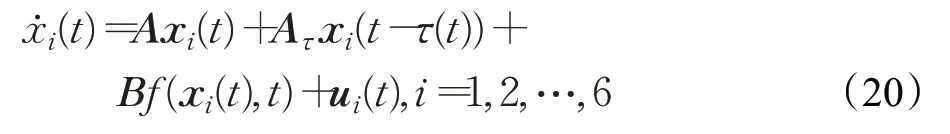
其中，A=-4,Aτ=-7,B=-0.03。

领导者的动力学模型为：

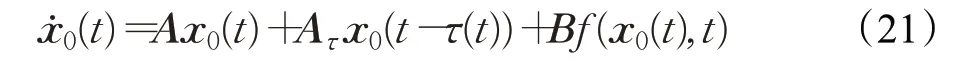
其他参数同例1，从图4和图5可以看出跟随者网络（20）与领导者网络（21）在采样控制（3）下可以实现完全同步。

图4 例2中x 0(t)和x1(t),x 2(t),…,x6(t)的轨迹图

4 结论

图5 例2中同质系统的误差轨迹图

本文研究了含时变时滞的非线性异质复杂网络在含输入时滞的采样控制下实现拟同步的问题。基于减少稳定性条件降低保守性的目的，在Lyapunov泛函中增加采样信息。利用Lyapunov-Krasovskii稳定性理论和线性矩阵不等式方法得出了保证非线性异质复杂网络实现拟同步的充分条件。并估计出实现拟同步的误差上界。同时验证了同质的情况，当异质网络变为同质时是可以实现完全同步的。最后，数值仿真证明了理论结果的正确性。