“以人为本”理念下交叉口缘石转弯半径取值研究

2021-06-23张士杰段竞泽

交通工程 2021年3期

费硕，张蕊，张士杰，段竞泽

(1.北京建筑大学土木与交通工程学院，北京 100044；2.北京建筑大学首都世界城市顺畅交通协同创新中心，北京 100044；3.北京建筑大学北京市城市交通基础设施建设工程技术研究中心，北京 100044；4.深圳市城市交通规划设计研究中心有限公司北京分公司，北京 100083)

随着“密路网、小街区”的城市布局倡导，“以人为本”的城市交通发展理念逐渐成为共识. 交叉口作为城市道路咽喉，在以往保证机动车通行效率的设计理念下，交叉口缘石转弯半径设计有利机动车快速右转，但对于部分右转机动车较少、行人及自行车交通量较大的交叉口，往往因右转车速控制情况不佳，导致“慢行友好”等先进设计理念难以落实. 交叉口设计的核心思想向“以人为本”转变后，缘石转弯半径的取值也宜关注交叉口慢行交通和机动车的冲突，为步行和自行车提供安全保障和通行便利.

当前缘石转弯半径的取值方法，第1类以标准和规范内容为主，我国《城市道路交叉口规划规范 GB50467—2011》[1]根据右转车速提出缘石转弯半径最小建议值. 美国公路与运输协会(American Association of State Highway and Transportation Officials AASHTO)在《公路与城市道路几何设计》[2]中主要考虑交叉口的预期交通量及车辆类型. 美国城市交通协会(National Association of City Transportation Officials NACTO)发布的全球街道设计导则[3]提出宜步行的活力街区，建议3～5 m无差别控制. 各类规范性文件中考虑的影响因素不同，导致设计取值有较大差异，且实际设计中弹性不足.

第2类为经验取值法，分析缘石转弯半径取值影响因素，建立数学模型并获得参考值. Fitzpatrick[4]观测了多个信号交叉口的车辆右转速度，结合缘石转弯半径得出85%位车速与缘石转弯半径及渠化方式的回归模型. 张雪琰[5]拟合得到缘石转弯半径与右转速度间关系，给出缘石转弯半径推荐值. 该类方法具有一定科学性和逻辑性，但由于交叉口交通环境复杂，建模数据有限，其实用性较弱.

微观仿真作为冲突分析的有效手段，可真实模拟不同群体在各种交通环境下的微观交通行为. 文献[6-7]均对行人与机动车在共享区域内的混行干扰现象建模，使混合交通流能按各自固定的轨迹行驶. 李珊珊[8]引入行人减速避让机制，基于车辆动力学理论、广义力模型，并考虑自行车期望路径，建立描述平交路口三者混行干扰的组合模型，实现了交叉口冲突对象的全覆盖，但由于冲突机制复杂，过街行人与右转机动车及非机动车的冲突特性描述不够细致，模型仍有较大改善空间.

在关注慢行交通安全的研究背景下，本文拟建立能细致描述交叉口过街行人与右转自行车、右转机动车冲突行为的微观交通仿真模型，作为以慢行交通为主的交叉口交通分析工具，在“以人为本”设计理念下，研究不同缘石转弯半径对行人过街交通质量的影响，据此提出交叉口缘石转弯半径推荐值，为交叉口精细化、人性化设计提供分析方法和思路.

1 交叉口混合交通流模型改进

社会力模型已广泛用于微观交通仿真，通过将个体运动所受影响量化为物理力，得到个体每一时刻状态和连续的运动轨迹. 从交叉口行人过街角度出发，主要冲突对象为右转机动车及右转自行车，故本文将三者纳入社会力仿真系统，考虑不同群体交通特性差异以及对通行效率、交通安全的需求，改进社会力模型. 为了提高微观仿真的计算效率，假设绿灯亮起后，过街直行非机动车流以较快速度通过冲突区域，对交叉口冲突干扰影响较小，建模时不予考虑.

1.1 社会力模型改进

1.1.1 个体期望速度

期望速度反映个体通行效率，在社会力模型中为固定值. Lakoba[9]发现行人过街的期望速度是实时变化的，并由自身期望速度和周围行人的平均速度共同决定. 实际调查也发现，交叉口区域行人与自行车密度较高时，个体将选择跟随群体前进，期望速度减小，而右转区域出现排队时，机动车期望速度也相应下降. 据此交叉口行人、自行车和机动车的期望速度变化情况见式(1)：

(1)

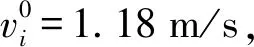
1.1.2 右转自行车与过街行人混行干扰

自行车在接近人行横道时，为减小穿越过街行人的阻力，会选择降低车速跟随前方自行车行驶，即自行车的跟随现象.王占中[10]在研究自行车过街行为时指定了自行车间跟随力，并认为当两辆自行车间距dbj满足ε1≤dbj≤ε2时，后方自行车会加速跟随前车过街，一旦两车间距过大或过小，跟随行为就会消失.本文引用其理论及参数标定成果，右转自行车穿越过街行人时的跟随力为式(2)：

(2)

式中，Abj为该作用力强度，取Abj=16；Bbj为该作用力影响距离，取Bbj=4 m；rbj为两骑行者半径之和；nbj为由骑行者b指向骑行者j的单位向量；ε1、ε2为常数，取ε1=0.5、ε2=2；ωbj为各向异性系数，有ωbj=(λb+(1-λb)(1+cosφbj)/2)p，表示自行车仅受前方车辆的跟随力作用，其中取λb=0.3，φbj为个体j与个体b运动方向的夹角，p为系数，且仅有φbj在30°～330°时，p=1；否则，p=0.

为了保障行人过街交通安全，右转自行车对行人产生干扰，但不与行人发生接触，故不考虑身体挤压或滑动摩擦的物理力，此时行人与自行车间作用力为：

(3)

式中，Aib为作用力强度，取Aib=2.25；Bib为作用力范围，取Bib=3 m；rib为两者半径之和；dib为行人与自行车质心距离.

1.1.3 右转机动车与过街行人混行干扰

与自行车相比，机动车跟驰行为更加明显.若用原始社会力模型刻画，其中仅包含车辆间相互作用力，仿真过程可能出现后车穿越前车的情景，与现实中减速跟随的行为特征不符.对此Helbing[11]引入跟随力对模型进行完善，当前车辆c与前车c-1之间的相互作用力fc,c-1可近似为跟随力，用于描述后车根据速度和与前车距离等因素，采取加速或减速措施，跟随前车行驶的行为.跟随过程中，一旦后车与前车距离足够远(超过某临界值d0，根据调查取d0=97.78 m)时，后车受前车跟随力影响很小，可根据自身意愿选择加速、减速或维持某期望速度行驶，故引入判断参数p1，反映两车距离与临界值的关系.曹宁博[12]根据其理论，建立交叉口右转机动车跟随模型，此处参考文献[11-12]理论，并引用部分标定结果，车辆间跟随力表示为：

(4)

式中，τc、τc分别表示机动车加速与制动时间，取τc=2.4 s、τc=0.77 s；vc为当前车速度；vc-1为前车速度，若vc-1>vc，则Θ(Δvc)=1，否则为0；若vc>vc-1，Θ(Δvc)=1，否则为0；Δvc为前后车速度差；Bc.c-1、Bc,c-1分别为加速及减速作用范围，取Bc.c-1=5.59 m、Bc,c-1=8.62 m；dc+Tcvc为安全距离，其中dc为最小车辆间距，Tc为车辆反应时间，根据调查取dc=1.38 m、Tc=0.74 s；dc,c-1为前后两车在所行驶车道上的净距离，当两车之间的距离大于或等于临界值d0时，p1=0，否则p1=1.

同理，右转机动车对行人的干扰不考虑接触情况，行人与机动车间作用力为：

(5)

式中，Aic为作用力强度，取Aic=5.5；Bic为作用力范围，取Bic=5.8 m；ric为两者半径之和；dic为行人与机动车质心距离.

1.2 仿真结果验证

基于改进的混合交通流微观模型，利用Pycharm进行平台构建及编译，完成过街行人、右转机动车和非机动车速度和加速度实时更新，实现不同交通个体的移动. 为验证模型有效性，读取仿真过程中行人对右转机动车和右转自行车可穿越间隙的接受和拒绝情况，并与实际调查结果进行对比，如表1、表2所示. 结果表明，所建微观仿真模型能较好反映交叉口混行情况，可基于此进行交叉口缘石转弯半径取值研究.

表1 行人对右转机动车间隙选择概率对比

表2 行人对右转自行车间隙选择概率对比

2 交叉口缘石转弯半径取值试验设计

交叉口缘石转弯半径减小时，驾驶员为保持横向稳定性，通常会降低车速，此时有利于行人安全及快速通过交叉口，由此设计场景并进行仿真试验，探究不同缘石转弯半径对过街行人和右转机动车交通质量的影响.

2.1 仿真试验交叉口设计

仿真试验交叉口如图1所示，为两城市次干路以90°相交，横断面形式均为3幅路(含机非分隔带)，两条道路平面设计指标(机动车道、非机动车道宽度)取值相同. 设置右转车辆类型为小客车，相交道路设计速度均为60 km/h，进口道有右转机动车专用道且设计速度为30 km/h，无右转专用相位. 对照我国《城市道路交叉口规划规范 GB50467—2011》，该情况下缘石转弯最小半径为20 m，为探究以人为本理念下交叉口设计指标，试验时缘石转弯半径取为5～20 m.

图1 仿真试验交叉口示意图/m

2.2 评价指标设计

试验中选取行人过街延误及右转车头间距作为评价指标，体现行人过街质量及右转车辆驾驶体验. 服务水平是行人过街质量的常用评价方法，美国道路通行能力手册《HCM2010》[13]中将行人平均延误作为行人流受到干扰的信号交叉口服务水平分级依据，以此反映行人过街舒适程度. 在不考虑信号控制影响的情况下，行人延误可认为是右转机动车驶入冲突区域前后过街行人的避让及等待时间.

右转车头间距反映前后两车的前端通过同一地点的时间差. 车辆在一定右转运行速度下，车头间距的变化一般是由于驾驶员面对环境变化作出的反应存在个体差异所产生的，如受到侧向非机动车干扰改变行驶轨迹. 右转车头间距的增大有利于产生行人安全过街的间隙，行人步行交通感受好，该指标既可衡量车辆驾驶体验，同时可作为行人过街交通质量的辅助评价指标.

2.3 流量设置

采用控制变量法，行人过街延误试验将过街行人和右转自行车流量设为固定值，进行3组不同右转机动车流量试验；右转车头间距试验设置固定的右转自行车和右转机动车流量，进行3组不同过街行人流量试验. 根据调查结果，流量设置如表3.

表3 不同试验流量设置人·h-1

3 交叉口缘石转弯半径取值研究

3.1 缘石转弯半径与行人过街平均延误

对3组右转机动车流量下的不同缘石转弯半径进行仿真，得到各右转机动车流量下行人过街平均延误随缘石转弯半径的变化情况，如图2所示.

图2 不同缘石转弯半径下行人过街延误均值分布

综合3组右转机动车流量下的行人过街平均延误情况，得到以下结论：

1)相同缘石转弯半径下，行人过街平均延误与右转机动车流量呈正相关关系，500 veh/h和1 000 veh/h下不同缘石转弯半径的行人过街平均延误均小于10 s，1 500 veh/h时行人过街平均延误均大于10 s；

2)在不同的右转机动车流量下，行人过街平均延误均先随缘石转弯半径减小同步下降，半径小于10 m后，行人过街平均延误均出现上升；

3)行人过街平均延误的离散程度随右转机动车流量的增加而下降.

分析上述结论原因，首先是缘石转弯半径的减小导致右转车辆降低车速，此时可供过街行人穿越的安全间隙增加，延误减小，过街交通质量提升. 但若驾驶员减速等待时间较长，即使可供右转车辆通过的间隙很小，也可能出现车辆抢行穿越的现象，后方驾驶员由于心理作用，选择紧随前车通过，行人过街延误再次增加并抵消了原先降低的部分. 其次，当右转机动车流量较大时，驾驶员为避免排队，在跟随前车的同时通过缩小车辆间距，使过街行人无法寻获安全的穿越间隙而继续等待，增大的了行人过街延误，也削弱了缘石转弯半径对行人过街延误的调节效果.

3.2 缘石转弯半径与右转平均车头间距

试验中在人行横道末端设置检测点，统计右转机动车面对过街行人穿越时平均车头间距的变化情况. 对3组过街行人流量下的不同缘石转弯半径进行试验，得到各过街行人流量下右转车头间距均值与缘石转弯半径的关系，如图3所示.

图3 不同缘石转弯半径下右转车头间距均值分布

综合3组过街行人流量下的右转平均车头间距分布结果，得到以下结论：

1)过街行人流量为1 500人/h，各缘石转弯半径下的右转车头间距均值最小，2 000人/h各半径下右转车头间距均值较1 500人/h整体上升幅度较小，2 500人/h下右转平均车头间距较2 000人/h整体增长幅度较大；

2)随着缘石转弯半径减小，各过街行人流量下的右转车头间距总体均呈上升趋势，半径为10～20 m时，各过街行人流量下的右转车头间距增长率均较小，小于9～10 m后右转车头间距增长率变大；

3)右转车头间距均值的离散程度随过街行人流量增大而减小.

过街行人数量较少时，由于孤单、畏惧等心理，会谨慎寻找可供穿越的安全间隙，此时右转机动车通行效率较高，右转车头间距多受缘石转弯半径影响；随着过街行人流量增长，面对右转机动车干扰占据一定心理优势，会选择时机结群通过，使右转机动车通行变得不连续，并在缘石转弯半径的共同作用下，导致右转车头间距显著升高. 另一方面，右转车头间距增大表明，驾驶员受到半径减小带来的冲击作用，感知的驾驶难度、发生事故的风险升高，该情况下驾驶员会选择控制车速，有利于及时发现前方过街行人并采取避让措施，但长时间易造成急躁等负面的驾驶情绪，不利于避免与过街行人的冲突.

3.3 缘石转弯半径取值分析

上述2组仿真试验中，在机动车交通量较小且行人与自行车交通量较大时，可获得较小的行人延误及较大的右转车头间距，行人过街等待时间短，过街服务水平较高. 对于右转车辆，行人过街交通量的提高虽然加大了右转车头间距，但未出现明显的车辆排队现象，右转驾驶体验较好. 此外，缘石转弯半径的减小对降低右转车速也效果较为明显，半径为20 m时，统计得到实际右转车速均值为28.3 km/h，半径为15、10、5 m时分别为24.2、18.7、13.3 km/h，右转车速的减小极大降低了行人事故风险及伤害严重程度，保障行人过街安全.

根据仿真试验结果，综合行人过街质量和右转车辆驾驶体验，在3.1中所述交叉口类型及设计参数条件下，缘石转弯半径取10 m为宜，小于《城市道路交叉口规划规范 GB50467—2011》中相同条件下20 m的取值，表明在以人为本的交叉口设计理念下，缘石转弯半径需进一步减小，引导右转机动车降低速度，实现交叉口慢行交通的空间和安全需求.

“以人为本”的交叉口设计理念下，首要目标为保障行人交通质量，尽量做到不同群体的交通质量均衡. 缘石转弯半径应根据交叉口流量组成进行取值，通过仿真分析获得行人交通质量指标，过街行人流量较大时，缘石转弯半径应取较小值；右转机动车流量占比较高，或公交车、货车等大型车辆频繁驶入时，缘石转弯半径应适当加大.