基于“窄马路密路网”布局理念的路网容量研究
2021-06-23张晓楠
张晓楠
(郑州市规划勘测设计研究院 , 郑州 450052)
1 概述
根据《中国主要城市道路网密度检测报告(2019年度)》[1],2019年度我国主要城市214个行政区(县)的路网密度平均值为6.3 km/km2,其中路网密度超过8 km/km2与10 km/km2的行政区(县)占比分别为16%与3%. 由此可见,我国主要城市的道路布局大多数以“宽马路、稀路网”为基本原则,由此引发交通拥堵、交通安全等诸多社会问题.
针对传统“宽马路、稀路网”的道路布局引起的社会问题,“窄马路、密路网”成为我国城市规划解决交通问题的新途径. 2016年2月,中共中央国务院印发《关于进一步加强城市规划建设管理工作的若干意见》(以下简称《意见》),《意见》提出要树立“窄马路、密路网”的道路布局理念. 2018年4月,中共中央、国务院对《河北雄安新区规划纲要》(以下简称《纲要》)做出批复,纲要提出:起步区路网密度达到10~15 km/km2. 《意见》的发布、《纲要》的批复,表明无论是国家政策还是国家新区的建设,都在提倡“窄马路、密路网”道路布局理念的实践.
城市的路网容量无论在城市交通规划、城市交通管理政策制定等方面都是重要的决策变量. 研究“窄马路、密路网”道路布局理念的路网容量,寻找其计算方法,对于更加精确的获取路网承载数据,为交通规划、交通政策制定、交通管理等提供重要的决策支持.
路网容量研究最早开始于20世纪50年代,经过Ford等[2-5]交通学者的长期研究,包括割集法、时空消耗法等多种路网容量模型先后被提出. 我国对于城市道路路网容量的研究开始于20世纪80年代,大多是基于国外的研究成果,针对我国国情和具体情况,对模型加以改进. 我国学者的早期研究成果中,关忠和[6]利用“时空消耗法”的理论,研究我国城市道路路网容量,提出了道路占有率的概念. 陈春妹[7]提出城市路网的时间特性,并给出了路网容量的研究周期. 章锡俏等[8-11]诸多学者从时空资源利用、路网节点、通行能力等角度,分别研究了特定情形下的路网容量. 由于现有研究成果多停留在理论层面,模型实用性不高,对“窄马路、密路网”道路布局理念下的路网特性考虑不够全面.
本文针对目前国内“窄马路、密路网”的道路布局趋势,对该布局理念下的路网容量模型进行研究. 以时空消耗理论为基础,分析在窄路密网条件下路网参数的变化情况,并对路网容量模型进行修正,构建窄路密网下的城市道路路网容量模型.
2 相关概念
根据技术规范中规定的技术标准与相关城市规划经验,定义“窄马路、密路网”道路布局理念下有关指标.
路网密度:根据《规范》中道路等级的划分,将窄路密网道路布局理念下的道路分为干道与支路,其中干道包括快速路、主干路、次干路. 在窄路密网道路布局理念下,干道路网的路网密度一般为(4~5) km/km2,支路路网的路网密度一般不小于6 km/km2,因此,本文中将窄路密网条件下的路网密度最小值定为10 km/km2.
路网级配:根据《规范》,道路等级越高、其相应等级的路网密度越低,路网级配呈金字塔状分布. 根据《规范》以及相关城市规划经验,窄路密网布局理念下各等级道路的级配按照快速路、主干路、次干路、支路的顺序排列为1∶2∶3∶7.
道路宽度:干道包括快速路与主次干路,以双向四车道及以上为主,因此干道道路宽度为24~50 m;支路为双向两车道或单行道道路,其宽度为10~20 m之间.
3 路网容量模型
3.1 时空消耗理论
在城市路网中,小汽车行驶时需要消耗城市路网的时间与空间资源,在城市交通规划、城市交通管理等实践中,都以小汽车行驶时的时间或空间资源管理为突破点,寻找解决交通问题的新途径. 城市道路的空间资源从广义上来讲为城市道路红线内的面积总和,由于目前交通问题的产生基本来源于小汽车交通,因此,对于小汽车来讲,道路的空间资源为城市路网中机动车道的总面积. 城市路网的时间资源一般来说为城市路网的通行时间.
在“时空消耗”理论中,路网容量反映了城市路网时间与空间总资源与居民出行消耗时间与空间资源的关系. 因此,路网容量是路网的时间与空间总资源与居民单次出行消耗资源的比值. 本文以该理论为基础,构建路网容量的理论模型:
(1)
式中,C为路网容量;CR为城市路网提供的时空总资源;CP为居民出行平均消耗的时空资源;L为路网运营长度;T为路网运营时间;D为道路运营宽度;lC为小汽车行驶时所需要的道路长度;d为小汽车行驶时所需要的道路宽度;t为平均出行时间;h为研究时段内道路上车辆的车头间距;k为机动车道的车辆密度;l为居民的平均出行距离;v为机动车行驶速度.
时空消耗法理论模型中,参数k(1条机动车道上的机动车交通密度)、v(机动车行驶速度)、l(居民平均1次出行距离)可通过城市综合交通调查中获取,视城市情况而定.其余参数都需要独立建模求解,下面对模型中的参数进行建模.
3.2 城市路网中道路的运营长度(L)
“窄马路、密路网”道路布局理念下,城市机动车道的有效运营长度为机动车总长度减去交叉口范围内机动车道长度.路段与交叉口构成路网的基本组成单元,如图1所示.快速路与低等级道路相交时,一般采用立体交叉,在交叉口处基本不会产生延误,因此,对于快速路,其有效运营长度等于快速路的长度.
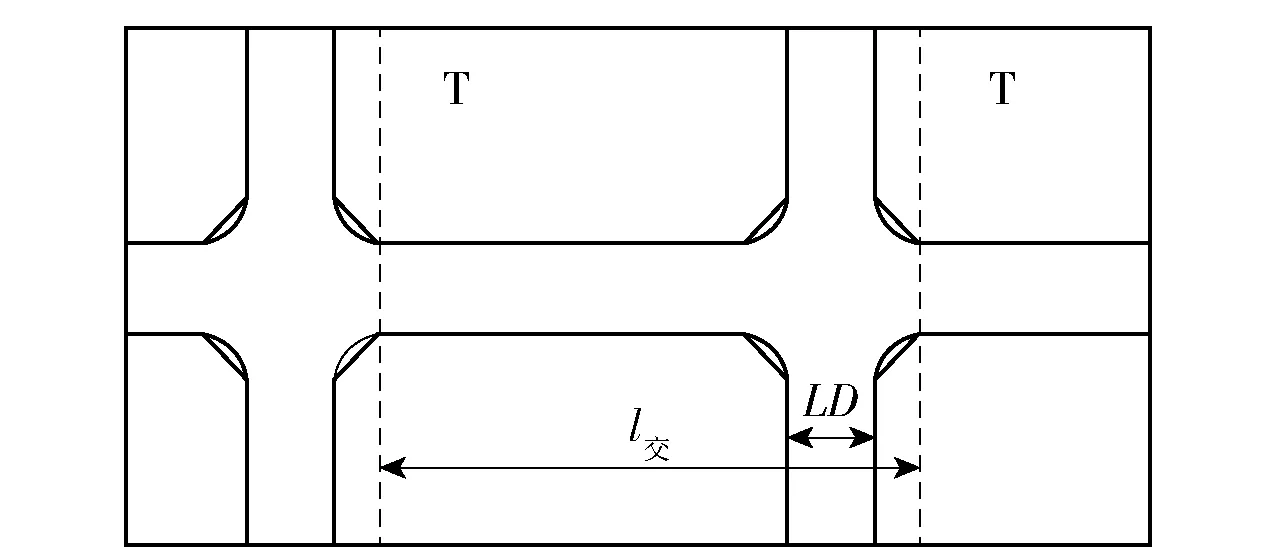
图1 路网组成基本单元
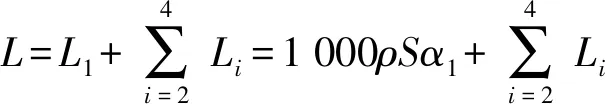
(2)
Li=1 000ρSαiFLi
(3)
(4)
式中,L为城市路网中道路运营总长度;i为城市道路的等级;Li为城市道路中道路等级i运营长度;αi为城市道路中道路等级i的比例;ρ为城市道路网密度;S为路网区域面积;FLi为运营长度系数;LDij为城市道路中等级i道路与第j条道路相交的道路红线宽度;mi为与城市道路中等级i道路的交叉口数量.
3.3 城市路网中道路的运营宽度(D)与小汽车行驶时所需要的道路宽度(d)
根据《城市道路交通规划设计规范》(GB50220—95),城市主干路及以下道路设计速度均不超过60 km/h,快速路设计速度最高一般为80 km/h,小汽车在行驶过程中所需要的横向安全距离一般在3.25 m范围内,大型车所需要的横向安全距离在3.5 m范围内.
在小汽车行驶过程中,其所需要的横向宽度一般在1条车道的宽度范围内,当1条车道被1辆小汽车占用,虽然该小汽车没有将车道的横向距离全部占用,但是其剩余的距离不满足另一辆小汽车的通行. 因此,无论车道数是几条,单车行驶所需要的横向宽度为1条车道的宽度. 道路有效宽度为车道宽与车道数乘积. 因此,道路的有效空间资源可用道路的有效营运长度与道路有效宽度的乘积表示.
3.4 城市路网中道路的运营时间(T)
本文以高峰小时为研究时段. 城市路网中道路的运营时间为研究时段减去路网延误时间. 其中,路网延误时间为车辆在交叉口行驶时,由于车辆排队、等候、起步停车等造成的延误. 由于快速路不受交叉口的影响,因此,快速路的运营时间比例为1. 路网运营时间用FT表示,则路网运营时间可表示为式(5)~(7):
T=FTTO
(5)
(6)
(7)
式中,FTi为城市路网运营时间比例;TO为研究时段,本文以高峰小时为研究时段,因此本文3 600 s;lt为交叉口间距;vi为车辆在等级i道路路段的车速;a,b分别表示汽车在起步与停车时的加速度;Δi为汽车在路网交叉口的平均等候时间.
3.5 模型参数修正
3.5.1 交叉口交通组织方式的修正
将交叉口的交通组织方式分为3类,包括双向与双向交叉、双向与单向交叉、单向与单向交叉.相比于双向道路交叉口的交通组织,单向道路的交叉口交通组织更为简单,冲突点更少,交通效率更高.在窄路密网的道路布局理念下,路网的形态将更有利于单向交通组织,因此路网的冲突点将减少.本文以交通组织修正系数的形式对路网容量模型进行修正.交通组织修正系数可表示为式(8)(9):
(8)
(9)
式中,fa为交通组织修正系数;γi为城市路网中i类交叉口交通组织方式冲突点的降低率;qi为城市路网中i类交叉口交通组织方式的数量;pi为城市路网中i类交叉口交通组织方式冲突点总数;po为双向与双向交叉时冲突点总数;q为交叉口总数.
3.5.2 横断面形式的修正
道路横断面在窄路密网理念下与宽马路希路网相比将发生较大变化.支路的数量将大幅增加,因此道路横断面的变化对容量的影响不容忽略.本文以交通横断面修正系数的形式对路网容量模型进行修正.
4块板的道路横断面中,由于机动车道与非机动车道、机动车道与对向车道都采用物理隔离的方式,因此,在4块板的道路横断面中,汽车行驶时既不受非机动车与行人的影响,也不会受对向车道车辆的影响.因此,在4块板的道路横断面中,横断面形式的修正系数:
fb1=1
(10)
3块板的城市道路横断面中,机动车道与非机动车道采用物理隔离的形式,但是对向车道没有采取物理隔离.机动车在行驶过程中不受非机动车与行人的干扰,但是受对向车辆的干扰,因此,3块板道路横断面的修正系数为:
fb2=a+bQ
(11)
2块板的道路横断面中,对向车辆采取物理隔离,机动车与非机动车道没有采取隔离.车辆在行驶过程中会受非机动车与行人的干扰,但是不会受对向车辆的干扰.因此,两块板道路横断面的修正系数为:
fb3=c+dX
(12)
1块板的道路横断面中,机动车与非机动车道、对向车道均没有采取物理隔离,因此车辆在行驶过程中,既会受非机动车与行人的干扰,也会受对向车辆的干扰.因此,其修正系数为:
fb4=e+fX+gQ
(13)
根据各横断面形式中路段的数量,基于各横断面形式的修正系数,构建窄路密网条件下修正系数模型:
(14)
式中,fb为横断面修正系数;lbj为横断面j的路段长度;Q为对向机动车道的机动车流量;X为非机动车流量.
3.5.3 交通需求与路网供给的匹配度修正
以交通需求与路网供给的匹配度作为修正系数对路网容量模型进行修正:
(15)
(16)
(17)
式中,βi为路段i的饱和度;βo为城市路网的平均饱和度;li为路段i长度;Vi为路段i交通量;δi为道路设计水平;COi为路段i的可能通行能力;在实际应用过程中,如没有具体交通数据时,fc一般取经验值0.7~0.9.
3.6 路网容量修正模型
根据对时空消耗模型参数中城市路网中道路的运营长度(L)、城市路网中道路的运营宽度(D)与小汽车行驶时所需要的道路宽度(d)、城市路网中道路的运营时间(T)以及交叉口交通组织方式的修正、横断面形式的修正、交通需求与路网供给的匹配度修正的讨论,得到窄路密网布局理念下,城市道路路网容量的修正模型.
(18)
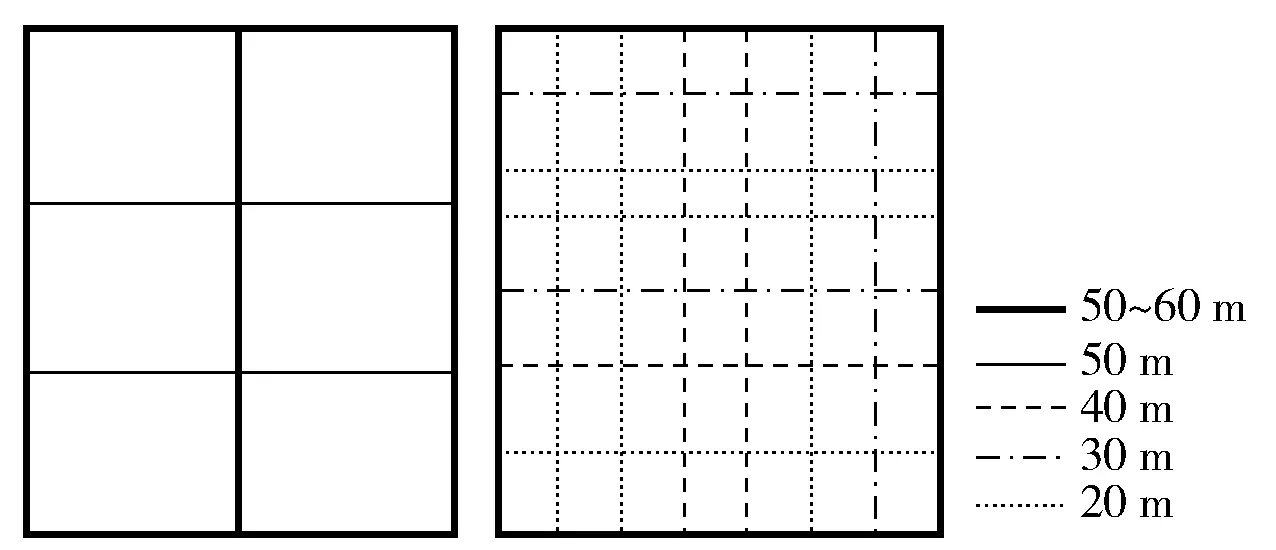
图2 “宽路稀网”与“窄路密网”路网布局
4 模型验证
本文以1 km×1.2 km的方格路网为案例. 按照 “窄马路、密路网”布局理念下的路网容量模型计算2种路网布局的路网容量. 对比路网加密前后的路网容量,在路网相同服务水平下,宽路稀网的路网密度由4.5 km/km2增加到窄路密网的12.8 km/km2,路网密度增加2.84倍,而路网容量由2 378 pcu/h提升至4 344 pcu/h,提升83%. 由2种路网布局下的路网容量结论对比发现,窄路密网的道路布局有助于路网容量的提升,但是路网容量的增加与路网密度的增加并不呈线性关系.
对于上述结论计算过程,部分模型参数的对比如表1所示:

表1 加密路网前后参数对比
通过对表1进行分析,路网容量的参数变化如下:
1)由于路网密度的增加,交叉口间距减少,由于交叉口行程的交通延误增加,导致路网的平均运营时间比例降低,平均出行时间增加.
2)由于路网采取更多的单向交通组织,交通冲突点减少,因此交叉口交通组织的修正系数增加.
3)由于支路规模的增加,车辆行驶受行人、非机动车以及对向车辆的干扰增加,道路横断面形式的修正系数降低.
4)由于窄路密网拥有更均匀的路网分布,交通需求与路网供给的匹配度更好,因此交通需求与路网供给的匹配度修正系数增加.
5 结论
以“窄马路、密路网”布局理念下的路网容量为研究对象,根据“窄马路、密路网”的路网特征,对路网密度、路网级配、道路间距进行了梳理研究. 以时空消耗理论模型为基础,对模型中的4个参数包括城市路网中道路的运营长度(L)、城市路网中道路的运营宽度(D)、小汽车行驶时所需要的道路宽度(d)、城市路网中道路的运营时间(T)进行详细分析. 此外,针对窄路密网道路布局,对时空消耗理论模型进行模型修正分析,共进行3次修正,包括交叉口交通组织方式的修正、横断面形式的修正、交通需求与路网供给的匹配度修正,并建立了各修正系数的计算模型. 基于上述分析,论文构建了窄路密网道路布局理念下的城市路网容量模型.
论文以一个1 km×1.2 km的方格路网为案例,分别对路网加密前后进行路网容量计算分析,对比研究路网加密前后路网容量与计算参数的变化,研究发现,窄路密网有助于提升路网的容量. 在本案例中,每平方公里的城市土地上,道路密度每增加1 km,路网容量增加237 pcu/h.
