感潮河道平面二维水流数学模型建立与验证
2021-06-23朱明栓张思慧江中林
朱明栓,张思慧,江中林
(1.福建船政交通职业学院 土木工程学院,福建省福州市仓山区首山路80号 350007;2.福建省兴禹源水利工程设计有限公司 设计部,福建省福州市鼓楼区福飞南路104号 350001)
闽江是福建的母亲河,也是我国重要的入海河流,其发源于武夷山脉南麓,为山溪性河流,水量丰沛,为福建省内第一大江河,横穿省会城市福州而过注入东海。闽江下游河段属感潮河段,长期受径流和潮流的双重影响,致使河流流态和形态复杂,流向多变且顺逆不定。闽江下游人类活动频繁,社会经济发达,近十几年来,一方面闽江上游河流电站的梯级开发,特别是水口电站的建成,使上游来沙量急剧减少,另一方面为满足经济建设对“闽江沙”进行了大量的开采。上游来沙量的减少和对“闽江沙”的过量开采,极大地改变了天然径流的水力条件和泥沙的运动规律,导致闽江下游河床急剧下切。为此,闽江下游河道问题已经成为制约社会经济发展、危害生态环境、影响人民生活的突出问题。闽江南港航道整治工程的尽快实施对开发南港航运资源、减轻福州市区的防洪压力、促进福州中心区域的防洪减压、促进福州中心区域闽江旅游资源的开发与经营有直接意义,并有利于闽江下游河沙的可持续开发利用和水环境的改善,对加快实施福州市的城市“东扩南进”战略、福建海西发展战略等都有十分重要的意义。因此迫切需要对该河段的水动力场和泥沙运动规律等问题开展深入的研究,以便于该段河道整治工程方案及相关工作的顺利开展。
对于描述水平尺度远大于垂直尺度的河流、海洋、湖泊等水体运动状态的物理量,当沿水深方向的变化相对于水平方向的变化小得多时,可将三维问题通过沿水深方向积分取平均,得到沿水深积分平均的平面二维简化形式[1]。文中应用平面二维水流数学模型研究闽江下游河段水流运动特征,为该段河道整治及感潮河流泥沙分布情况研究提供参考。
1 建模区域河道概况
闽江自淮安起,下游河道分为南北港,分别绕南台岛两侧流向下游[2]。闽江南港也称乌龙江,长约34km,位于福州市内南台岛南面,中段有大樟溪水流汇入,在马尾处与北港汇合,继而折向北进入通海河段,流经青洲、闽安峡谷至亭江注入东海,长约12km。河道坡降较上游变小,河水流速减缓,并受潮水顶托作用,致使河道曲折而宽浅,沉积作用显著,沙洲、边滩发育,泥沙淤积严重。南港是天然的泄洪排沙水道,接受大部分中游来沙,江面宽浅,大部分江面宽为1000~3000m,最宽处达4000m以上。模型建模区域为南港入口淮安至闽江入海口亭江,河道具体情况如图1所示。
2 二维水流数学模型
2.1 基本方程
连续性方程:
运动方程[3]:
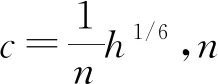
2.2 定解条件与求解
初始条件:
z(x,y,t)|t=0=zA(x,y)
u(x,y,t)|t=0=uA(x,y)
v(x,y,t)|t=0=vA(x,y)
边界条件:
对水边界Γ1
z(x,y,t)|(x,y)Γ1=zB(x,y,t)|(x,y)∈Γ1
对岸边界Γ2
u(x,y)cos(n,x)+v(x,y)cos(n,y)=0
其中,Γ1为水边界,Γ2为岸边界;cos(n,x),cos(n,y)为外法线的方向余弦。∂Ω=Γ1+Γ2,Ω为水、岸边界围成的平面区域[4-5]。
文中采用有限元中的Galerkin法来求解平面二维河道水流方程[6],对控制方程进行离散,设置变量并用Fortran语言编制计算程序。
3 模型中关键问题的处理
3.1 动边界的处理
在天然河道及河口处通常存在较大面积的沙脊和潮滩,它们随着水位的涨落时而裸露时而淹没,相应的水域面积也随着减小或增大,因此水边界的变化幅度比较大。在对此区域进行数值模拟计算时,为了较为真实准确地模拟落潮归槽、涨潮漫滩的潮流运动,使计算持续下去,有必要引进动边界技术。
建模区域位于闽江南港,此处江面开阔,河道流速减缓,且受潮水顶托作用,滩涂、沙洲发育良好,涨潮、落潮时的情况不一,从浅滩流态和计算稳定性来考虑需要做动边界处理。当前对动边界的处理方法有很多,常见的有水位判别法、冻结法、开挖法、切削法、窄缝法和线边界法。因为水位判别法具有清晰的物理概念、简单的实现过程和良好的计算效果,所以广泛推广应用[7-8]。同时,水位判别法还能对滩槽、露滩、沙脊等多种地貌并存的河流获得较高精度的潮流、潮汐全貌,故文中采用此法。
在实际计算中一般把潮滩区的动边界按二维问题来处理。对于平面上任一潮滩点(i,k),瞬时水深hi,k=Di,k+ζi,k,其中Di,k,ζi,k分别为(i,k)点的滩地高程及潮位。
落潮过程中,ζi,k<0,当hi,k≤hmin时,认为该点干出,不参与计算,且令其流速为0;反之,则认为该点淹没,参与计算。涨潮过程中,水边界线随潮位的上升向高滩推进,则计算网格点增多。因新增网格点原无潮位值,故取其周围4点(i+1,k),(i-1,k),(i,k+1),(i,k-1)中已淹水的诸点潮位的平均值。
ζi,k=
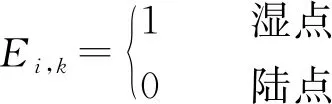
涨潮时,ζi,k>0,当hi,k≥hmin时,认为该点淹没,参与计算,反之则不参与计算。
3.2 网格的划分
河口地区的特点是水浅、岸线形状和水下地形复杂、存在各种形状的沙洲、滩涂和人工建筑物(导流堤等),导致该地区的潮流场通常十分复杂。就网格划分形式而言,不规则三角形网格非常实用,当前被广泛采用。不规则三角形网格有很多优点:1)可以很好地拟合水下地形和固边界形状,岸线和水下地形概化好;2)网格疏密自由控制,网格布设随意;3)通用性好,矩形网格可以看作是由若干个直角三角形组成的三角形网格,是不规则三角形网格的一种特殊形式。
闽江下游河段属于感潮河段,长期受径流和潮流的双重影响,致使河流流态和形态复杂,并且地形错综复杂、区域边界曲折多变,因此对该区域流态和水深的模拟存在一定的困难。根据上述地形变化的不规则特点和实际需要,模型采用灵活多变的不规则三角形单元计算网格,对重点区域进行网格加密,采用整体和局部相结合的模型建模方法建立二维水流数学模型。通过在河道的交汇口和弯道的地方适当加密,模型能较好地反映实际河流的地形地貌。同时为了提高工作效率,便于修改,编制了计算机单元自动剖分程序,实现了计算区域网格单元剖分自动化。
4 模型的调试和验证
4.1 资料选取
收集到的资料包括:
(1)2019年4月与9月实测的1∶1000和1∶5000闽江干流淮安至亭江段河道地形图;
(2)2013年12月和2018年2月南港至亭江段水文实测资料,包含潮位、流速资料;
(3)南港近远期规划资料;
(4)南港现有堤防情况。
模型研究区域为闽江下游淮安至河口亭江处,上游边界选取南港淮安断面、南港中段大樟溪江口特大桥断面和马尾附近北港壁头村断面,下游边界选取河口亭江断面。
4.2 边界条件及网格划分
采用2017年12月11日~12日的实测潮位作为模型区域进、出口断面的边界控制条件。
模型区域采用三角形网格进行剖分,本模型共有6461个节点,12262个三角形网格单元,网格步长控制在200~700m之间,模型区域的网格图如图2~图4所示。

图2 模型网格剖分图Fig.2 Model mesh subdivision
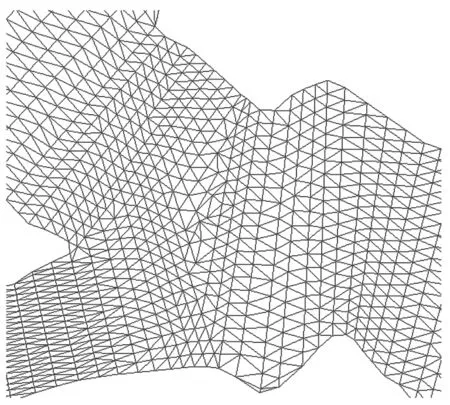
图3 大樟溪汇入处的网格剖分图Fig.3 Mesh subdivision map of the confluence of Da Zhang River
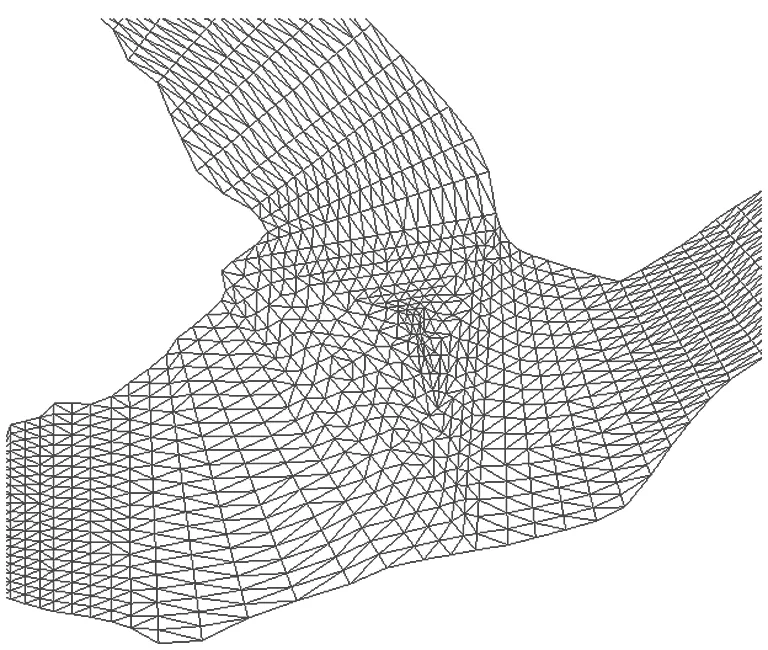
图4 南北港汇流处的网格剖分图Fig.4 Mesh subdivision of the confluence of the North and South ports
4.3 参数的选取
为了计算的稳定性要求,水流程序计算过程中时间步长必须满足:
式中:ΔLmin为计算区域内最小的三角形边长;Hmax为计算区域内最大的水深。
4.4 糙率系数
糙率的精度直接影响到模型的计算精度[9]。由于影响河道糙率的因素较为复杂,文中采用试算法对其进行调试。若模型计算误差过大,则不断调整糙率值,直至将误差控制在一定的范围内。最后确定合理糙率值的范围为0.025~0.045之间。
4.5 富裕水深的确定
本河段内滩地宽阔,且受潮汐和径流的双重影响,水流涨落起伏大,随着水流的涨落,水边界也会随之移动,因此,如何合理的模拟水流边界的移动,直接关系到模拟计算的成败[10]。模型中采取水位判别法来处理这类动边界问题,并经过调试取富裕水深为0.05m。
4.6 模型验证
模型采用2017年12月11日~12日的实测潮位、流速进行验证,计算值和实测值比较如图5~图9所示。由图可见计算的潮位、流速与实测值吻合情况良好,量值大小上虽有些波动,但基本相当。
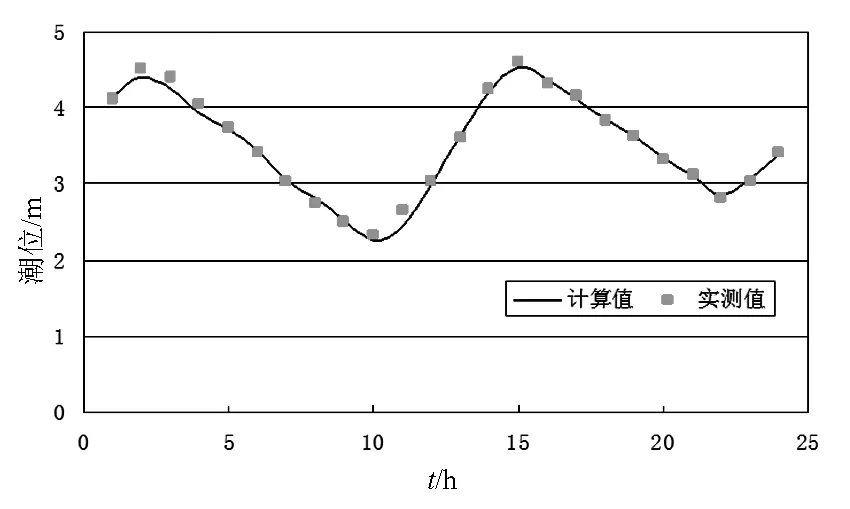
图5 洪塘大桥处潮位过程验证Fig.5 Verification of tide level process at Hongtang Bridge
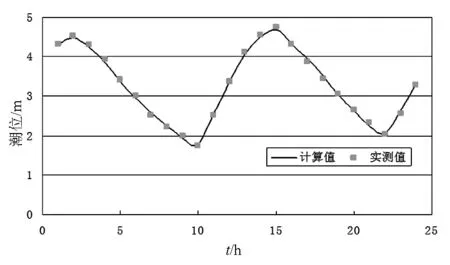
图6 浦上大桥处潮位过程验证Fig.6 Verification of tide level process at Pushang Bridge
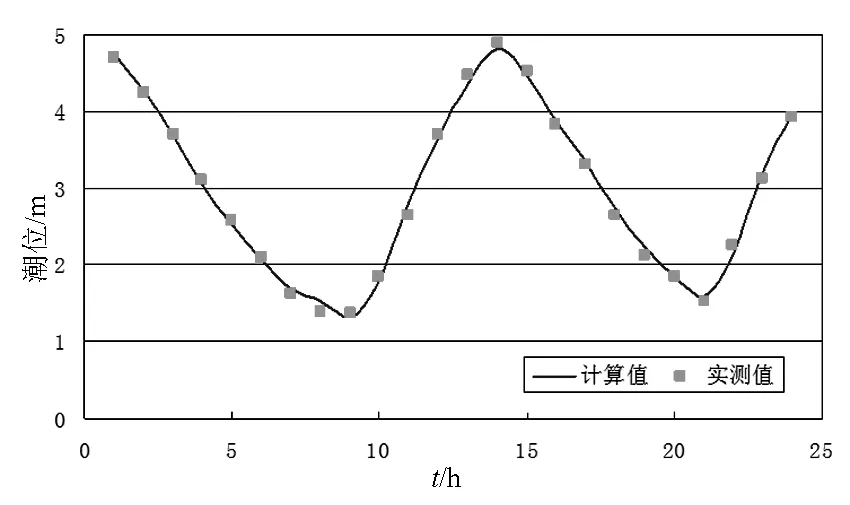
图7 湾边断面处潮位过程验证Fig.7 Verification of tidal level process at bay side section
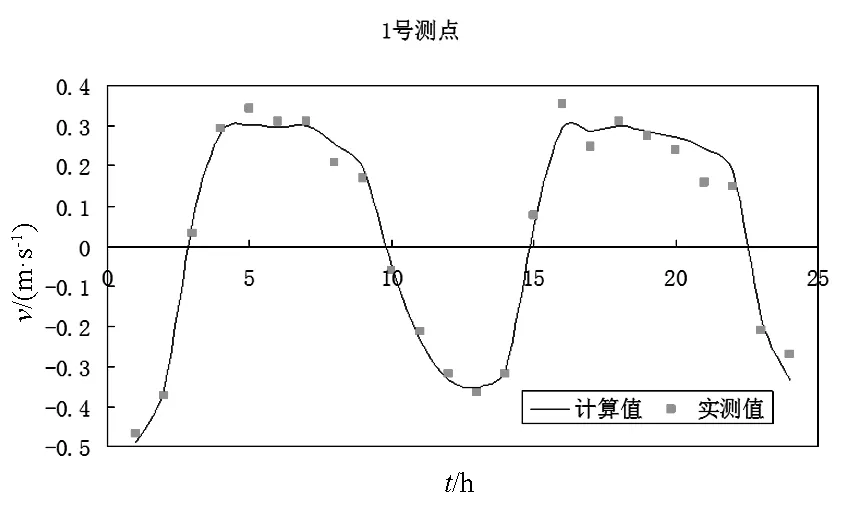
图8 科贡断面处测点流速大小验证图Fig.8 Verification diagram of flow velocity at measuring points at Kegong section
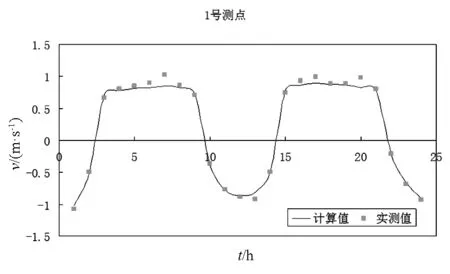
图9 湾边断面处测点流速大小验证图Fig.9 Verification diagram of velocity at measuring points at bay side section
图10~图13为计算区域内涨急、落急流场平面分布图,从图中可以看出流场平面分布和滩槽分布相一致,在大樟溪汇入口、马尾汇流口附近,水流流态较为平顺,能较好地复现水流形态。以上分析表明该模型的参数选取是合理的。
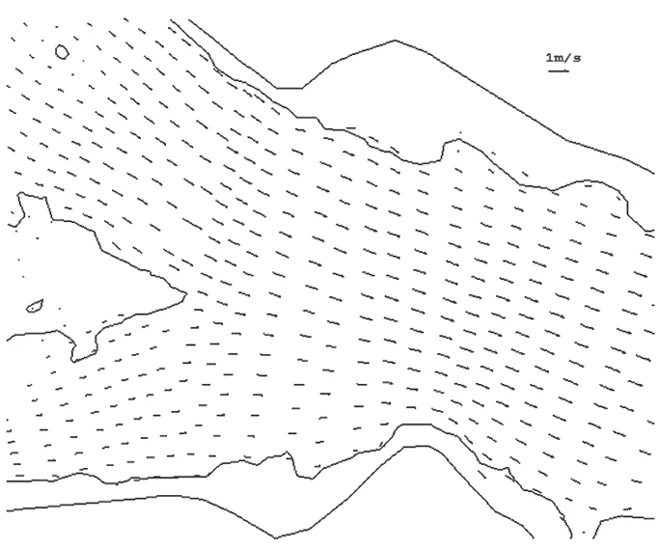
图10 河道落潮时的大樟溪与闽江交汇处流场图Fig.10 Flow field diagram of the confluence of Dazhang River and Minjiang River at ebb tide
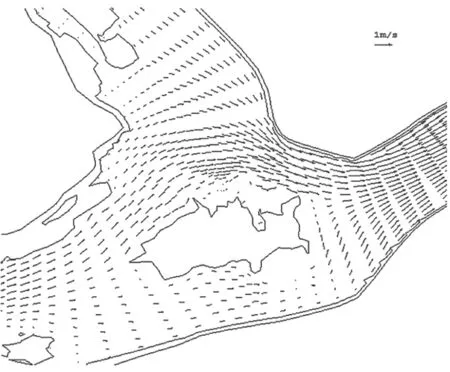
图11 河道落潮时的马尾汇流处流场图Fig.11 Flow field diagram of Mawei confluence at ebb tide
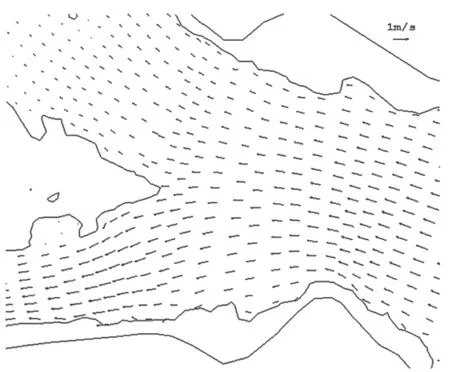
图12 河道涨潮时的大樟溪与闽江交汇处流场图Fig.12 Flow field diagram of the confluence of Dazhang River and Minjiang River at flood tide
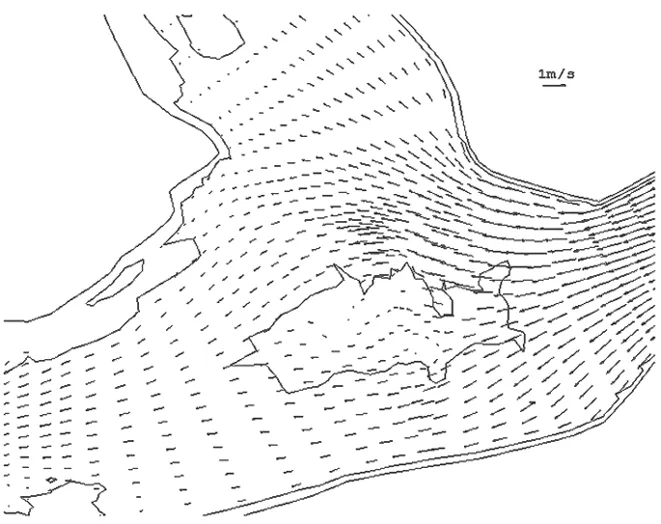
图13 河道涨潮时的马尾汇流处流场图Fig.13 Flow field diagram of Mawei Dazhang confluence at flood tide
5 误差分析
表1是河道中几个主要断面实测水位平均值与计算水位平均值的比较及相对误差分析,通过该表可以看出模型精度较高,误差均在4.55%以内。引起误差的原因可能是河道汇流、河床形态复杂等。
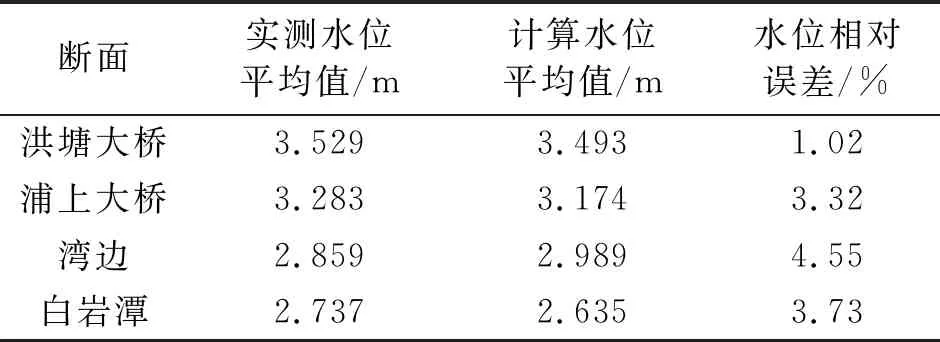
表1 主要断面实测水位与计算水位的比较Tab.1 Comparison between measured water level and calculated water level of main section
6 结语
闽江下游长期受径流和潮流的双重影响,特别是文中研究的南港河段,滩涂、沙洲发育良好,河流流态复杂多变。文中针对天然河道岸线曲折多变、地形复杂的特点,采用灵活多变的不规则三角形单元计算网格,应用有限元法建立起二维水流数学模型,并在模型中加入了动边界处理技术,使结果更符合实际情况。根据实测资料对二维水流模型进行调试、验证,结果表明计算值与实测值吻合良好,符合该区域潮流的运动特性。该研究成果为后期进行泥沙数值模拟和航道整治工程数值模型研究提供了良好的基础。
