浅谈初中数学勾股定理的拓展教学

■甘肃省张掖市高台县第二中学 方海国

一、勾股定理拓展教学的作用

在初中勾股定理教学中，教师可以对其进行适当的拓展教学，让学生对勾股定理具有更深的了解，从而帮助学生对数学这门学科具有更深的认知，也能够让学生明白与其相关的知识点，丰富学生的大脑，提高学生的发散性思维，有利于学生日后的数学学习和思考。还可以帮助学生对勾股定理进行证明，让学生知其然，亦知其所以然。如果学生只会应用前人的数学研究成果，而没有学会如何研究，这不但不会促进数学学习的进步，反而会造成数学研究的退步。因此，数学的学习要从基本知识下手，这样才能够逐渐提高学生的数学研究能力。通过对勾股定理应用的拓展，能够让学生明白数学不是简单地进行学习，而是要在现实生活中多应用，从而增加学生学习数学的乐趣，促进学生学习和研究数学知识。

二、勾股定理知识拓展

勾股定理指的就是在直角三角形中，两个直角边的平方和等于斜边的平方。在初中数学教材中论述的是直角三角形中三条边之间的关系，那么与直角三角形三条边相关的面积是怎样的呢？下面让我们一起来探索。教师通过多媒体设备与大屏幕进行连接，在PPT中展示了格子图形，并且在其中画了一个直角三角形，并与学生进行互动。教师：“同学们，我们都知道直角三角形三条边之间的关系，那么与三条边相关的面积是何种关系呢？”学生们陷入了沉思，教师将直角三角形中的每一条边都当作三角形的底边，然后做一个等腰三角形，如右图所示：

为了更好地让学生进行研究，教师将班级学生进行分组，四个人为一组进行组内学习和讨论，讨论通过直角三角形的三条边做出的等腰三角形是什么关系。在学生讨论的过程中，教师应该仔细观察学生的讨论，看看每个人在讨论时是如何阐明自身观点的，从而判断出哪些学生具有非常好的数学思维，然后可以多多与之交流和研究，也许会有新一代的数学家诞生。教师看到很多学生都在运用三角形面积公式在来回推导，最后发现都无法证明三个三角形之间的关系。这时，教师对学生们说：“如果没有快捷的方法去证明三个三角形之间的关系，我们可以运用比较笨拙的方法去进行计算，因为图形是在格子图形中进行绘画的，我们数一数格子的数量，不就能够明确三者之间的关系了嘛。”学生通过细心地观察和计算，发现两个直角边所形成的等腰三角形面积之和等于斜边形成的等腰三角形面积。通过此勾股定理知识拓展可以让我们明白，有时候数学的验证运用笨方法解题反而会更加简单，学生应该视情况而定，灵活运用数学方法去进行数学问题的解决，从而提高解题速率。在直角三角形的边上做图形是在二维层面上进行证明，如果引申为三维立体图形，那么它们之间又有什么关系呢？我们可以将直角三角形的三条边分别作为正方体的边长来做一个空间三维图形，如右图所示：

教师：“同学们，我们首先来探究它们表面积之间的关系，看一下是否满足两个直角边所形成的正方体表面积之和是否与斜边为棱长的正方体表面积，那么如何才能够计算出它们的表面积呢？”很多学生表示通过数格子来进行表面积的计算。教师：“数格子可以用于二维图形的面积计算，但是此为三维立体结构，无法运用查格子的形式进行表示，有哪位同学能够证明啊？”学生1：“老师，直角三角形的三边长分别是a、b、c，那么我们就能够知道正方体的棱长，正方体一个面的面积为棱长的平方，每个正方体都有6个面，那么三个立方体的表面积为6a2、6b2、6c2，而且我们知道a2+b2=c2，所以6a2+6b2=6c2。”教师：“既然我们证明了正方体表面积之间也是两个小正方体的表面积之和等于第三边，那么它们的体积是否也符合这个规律呢？”学生2：“它们的体积分别是a3、b3、c3，我们无法证明a3+b3=c3。”在进行勾股定理知识拓展的过程中，教师从直角三角形的三条边的关系拓展到二维平面关系，然后再由二维平面关系拓展到三维立体图形的表面积和体积之间的关系，从而能够在学生的大脑中形成科学的思考方式，有利于帮助学习树立全面思考的数学观念，同时也让学生学会了更多的数学证明方法，有利于学生数学素养的提升。

三、勾股定理方法拓展

初中数学教材中教师只是教授学生如何运用勾股定理进行解题，通过正向思维和反向思维来培养学生的发散性思维，但是并没有告诉学生该如何去推导勾股定理，学生只明白有这个定理的存在，却不知道是如何得来的。在进行拓展教学的过程中，教师应该针对勾股定理的推导方法进行教学讲解，从而让学生明白勾股定理是真实存在的，是经过推理而得来的，从而可以增加学生对勾股定理的信心，明白数学家是多么智慧，才能够想到这样的方法进行推理，有利于激发学生们研究数学的欲望。

首先，画出一个直角三角形ABC，AB是它的斜边，而BC和AC为直角边。并且已知AB的长度为c，BC的长度为a，而AC的长度为b。这时候，我们在斜边AB上取一个点D，使得BD=BC，并且在斜边AB的延长线上取一点E，使BE=BD。然后以B点为圆心，BD为半径做一个圆，如右图所示：

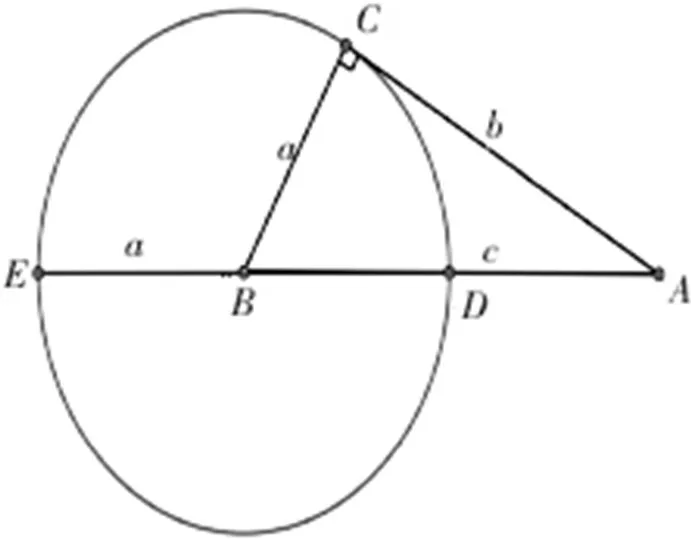
因为三角形为直角三角形，所以我们能够知道BC是垂直于AC的，所以AC为圆的切线。根据我们学习过的切割线定理可以得出AC2=AE⋅AD=(AB+BE)(AB-BD)=(c+a)(c-a)=c2-a2=b2。所以可以证明勾股定理为a2+b2=c2。

这个数学定理推导如果不给学生提示，学生是无论如何也想不到要做一个辅助圆来进行证明的。教师通过此过程的推理，能够让学生明白数学定理的推导需要具有非常多的数学知识为基础才能够进行证明，从而促进学生对数学基础知识学习的渴望，有利于学生的数学学习。

四、勾股定理应用拓展

数学是自然科学的一种，数学的研究主要是为了解决现实生活中的问题才被人研究。勾股定理在现实生活中具有非常重要的应用，比如在建筑工程中，很多时候需要判断墙面与地面是否垂直。这时候我们可以通过米尺在墙面上准确测量出30cm的距离，并进行标记，然后在地面上测量40cm的距离，同样进行标记。然后用米尺测量两个标记点之间的距离是否为50cm，如果测量结果为50cm，可以证明墙面与地面是真正的垂直关系，如果中间有一些偏差，我们可以知道墙面与地面不垂直。因此，勾股定理在工程建筑中的作用非常大。除此之外，修井、造车、建房等都需要运用到勾股定理。教师通过对勾股定理的应用进行拓展，能够让学生明白数学的学习是十分有意义的，我们应该学以致用，正确运用数学知识去更好地建设我们的祖国。

五、结语

综上所述，勾股定理拓展教学具有非常重要的作用，不但能够让学生进行勾股定理的应用，还能够让学生明白勾股定理是怎样去进行证明的，了解与之相关的知识点以及在现实生活中的应用。勾股定理拓展教学旨在让学生明白数学具有非常强的应用型，数学定理也都是为现实所服务的，同时还能帮助学生提高自身的数学思维，有利于学生对数学这门学科的深层次认知。