GFRP 加筋混凝土梁受弯性能有限元分析

冯永哲 辛冠玉

（长春工程学院 土木工程学院，吉林 长春130012）

1 概述

将FRP 筋材作为钢筋的替代品应用于混凝土结构可以有效的解决钢筋生锈对结构产生的危害[1-4]，各国学者针对FRP 加筋混凝土梁开展了广泛的研究，取得了一定的成果[5-6]。利用有限元方法对试验进行模拟能够提高研究效率，并能最大限度的拓展研究范围，有限元模型的建立方法是模拟试验能否成功的关键。本文通过建立有限元模型，对已有的GFRP 加筋混凝土梁进行有限元分析，利用计算结果与试验结果对比，探索GFRP 加筋混凝土梁有限元模型的建模方法。

2 试验设计

2.1 试件制作

FRP 加筋混凝土梁的破坏形态主要表现为FRP 筋拉断与混凝土压碎这两种破坏形态，试验根据不同配筋率共设计4 根梁，梁长均为2800mm，拟配混凝土强度均为C30。GCR-1 配置纵向受拉GFRP 筋2 根直径9.53mm；GCR-2 配置纵向受拉GFRP 筋2 根直径12.7mm；GCR-3 配置纵向受拉GFRP 筋3 根直径12.7mm；GCR-4 配置纵向受拉GFRP 筋3 根直径15.88mm；梁尺寸及配筋情况如图1 所示。

图1 GFRP 加筋混凝土梁配筋示意图

GFRP 筋弹性模量为40.8×103MPa，直径9.53mm 的保证抗拉强度为760MPa；直径12.7mm 的保证抗拉强度为690MPa；直径15.88mm 的保证抗拉强度为655MPa。试验采用的混凝土立方体抗压强度fcu为39.9 N/mm2。

2.2 加载方法及测量内容

梁加载采用三分点竖向加载方案，通过分配梁上的液压千斤顶逐级手动加载，开裂前荷载等级为2kN，开裂后荷载等级为5 kN，最后接近破坏时荷载等级为2kN。每级荷载加载完毕后，持荷2 分钟后记录各项测试数据。实验装置如图2 所示。

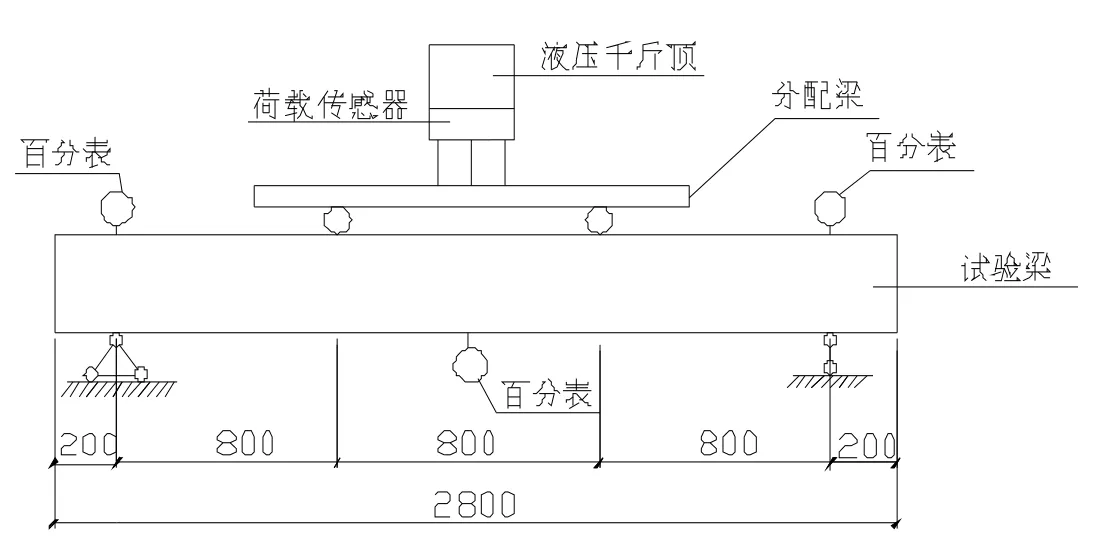
图2 GFRP 加筋混凝土梁试验装置

在试验梁的两支座、跨中位置分别布置3 个百分表，通过各表的竖向位移差测出梁跨中挠度。采用应变片测量梁受压区的应变和GFRP 筋应变。

3 GFRP 加筋混凝土梁非线性有限元分析

3.1 有限元模型的建立方式

在ANSYS 软件中，根据加强筋处理方式的不同，加强筋混凝土构件有限元模型的建立有三种方式，即分离式、整体式和组合式。

本文采用的是分离式有限元模型，并且认为GFRP 筋与混凝土粘结良好，不考虑GFRP 筋的滑移。

3.2 单元模型的选择

在ANSYS 软件中一般用SOLID65 单元来模拟混凝土单元，SOLID65 单元用于有加强筋或无加强筋的三维实体模型，能模拟压碎和开裂特性。该单元最主要的特点是对材料非线性处理，SOLID65 单元建立的混凝土模型具有开裂（沿三个正交方向）、压碎、塑性变形和蠕变的功能。此单元有8 个节点，每个节点有3 个自由度，即X、Y、Z 方向的平移。其几何形式可以是六面体、棱柱体和四面体[7]。在ANSYS 软件中采用分离式建模时，一般用LINK8 来模拟加强筋。LINK8 是一个不考虑弯曲的三维单轴拉-压杆单元，有2 个节点，每个节点有3 个自由度，即X、Y、Z方向的平移。此单元有塑性、蠕变、膨胀、应力刚化和大变形的功能[7]。为防止局压破坏，本文在ANSYS 中采用SOLID45 单元模拟刚垫块。SOLID45 单元也是八个节点的六面体单元，每个节点同样拥有x, y, z 三个方向的平移自由度。该单元有塑性、蠕变、膨胀、大变形、大应变和应力刚化功能。与SOLID65 单元相比，SOLID45 单元没有开裂和压碎功能[7]。

3.3 模型建立

采用分离式模型建立方法，混凝土用SOLID65 单元模拟，钢筋及GFRP 筋采用LIINK8 单元。未考虑钢筋与混凝土之间的滑移。首先建立实体，然后划分单元，再在模型上布置荷载和支座，如图3、4 所示。混凝土轴心抗压强度为26.72MPa，泊松比取0.2，裂缝开裂时，剪切传递系数取0.25，闭合裂缝的剪切传递系数取为0.95。输入混凝土单轴应力应变关系时，采用《混凝土结构设计规范》（GB50010-2015）[8]提供的计算公式算得的数据。钢筋的屈服强度221.5MPa，弹性模量为2.17x104MPa 钢筋单轴应力应变关系采用理想弹塑性模型。GFRP 筋采用线弹性本构关系，在LINK8 的参数中只需要输入截面面积和弹性模量即可。

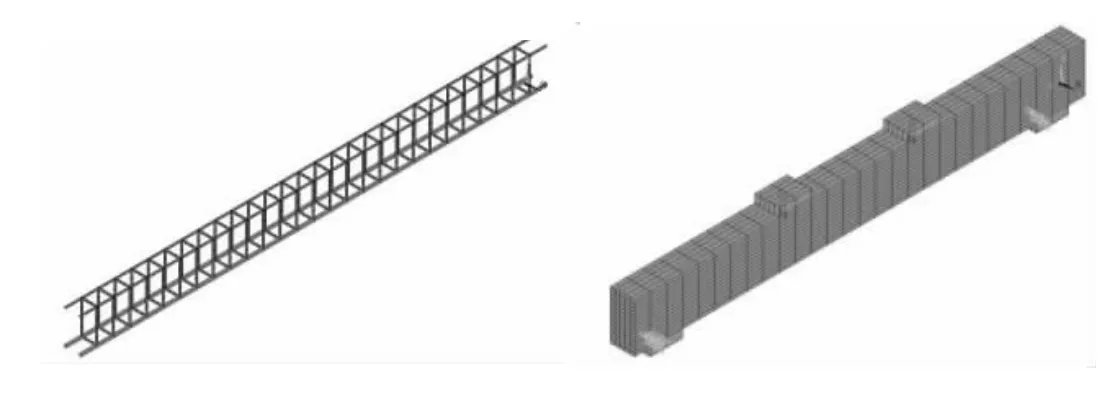
图3 GFRP 加筋混凝土梁LINK8 单元 图4 有限元模型加载图

4 有限元分析结果与试验数据对比分析

在计算过程中，GCR-1 的配筋率较低，裂缝发展迅速，造成ANSYS 软件的计算无法收敛，因而没有得出有效的ANSYS 有限元计算的数据。其余三根梁的计算收敛效果很好，荷载-挠度曲线对比如图5 所示。从图5 可以看出，ANSYS 计算的荷载挠度曲线与试验所得的荷载挠度曲线吻合很好，ANSYS 计算曲线也分为三部分：开裂前的线性发展阶段、开裂时的水平阶段和开裂后挠度增长较快的线性阶段，在各个阶段上，ANSYS 计算曲线与试验曲线都比较接近，且发展趋势相同，说明采用本文提出的有限元模型能准确模拟GFRP 加筋混凝土梁的变形发展过程。开裂挠度与极限挠度的比较如表1，从表1 的数据对比可知，ANSYS 有限元计算所得极限挠度与试验所得极限挠度吻合很好。

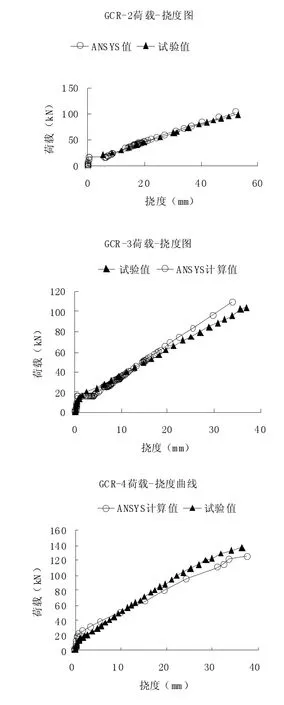
图5 荷载－挠度曲线比较

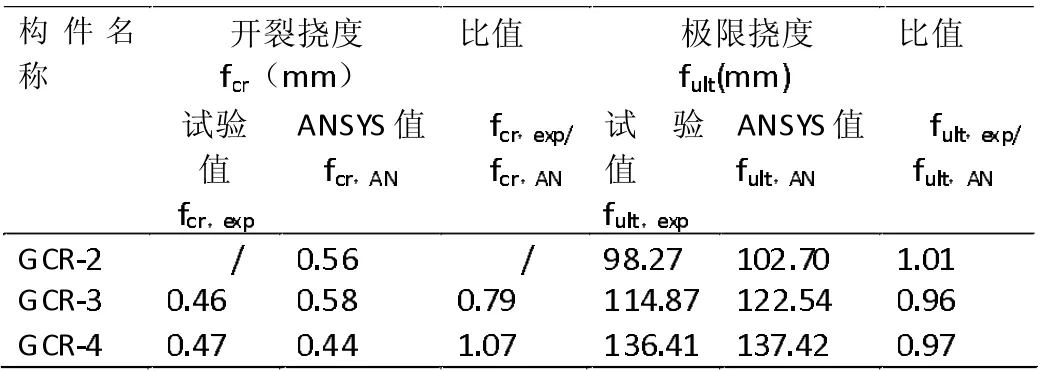
表1 开裂挠度和极限挠度比较

各梁中GFRP 筋的荷载－应变关系曲线对比如图6 所示。由图6 可看出：ANSYS 计算跨中位置处GFRP 筋荷载－应变曲线与试验所得曲线发展趋势形同，曲线吻合较好。只是在接近极限荷载阶段，二者有一定差距。通过以上分析可知，ANSYS 软件对GFRP 筋构件进行的有限元分析得到的GFRP 筋受力发展过程与实际情况接近。

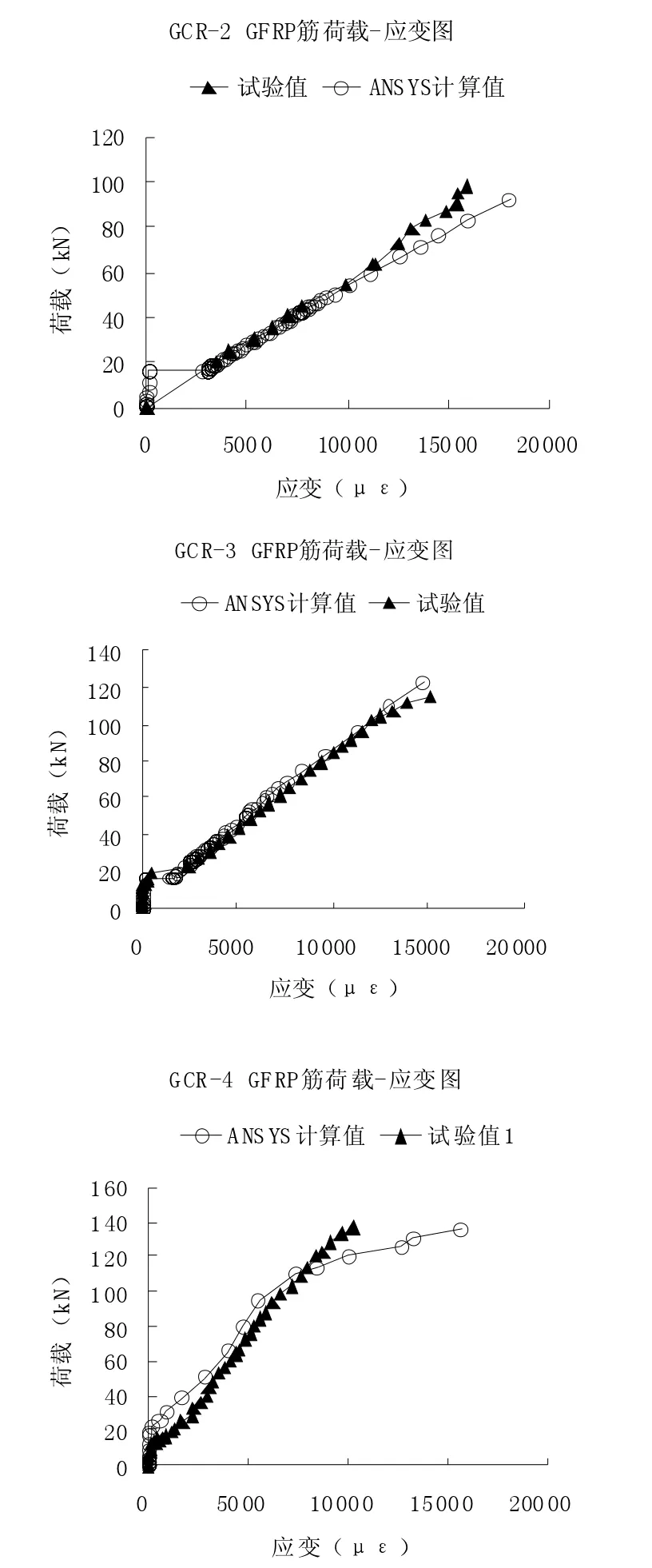
图6 各试验梁中GFRP 筋荷载-应变曲线

各梁的开裂荷载和极限荷载的对比如表2。由表2 知，ANSYS 非线性有限元分析所得各GFRP 加筋混凝土梁极限荷载值与试验值吻合很好。

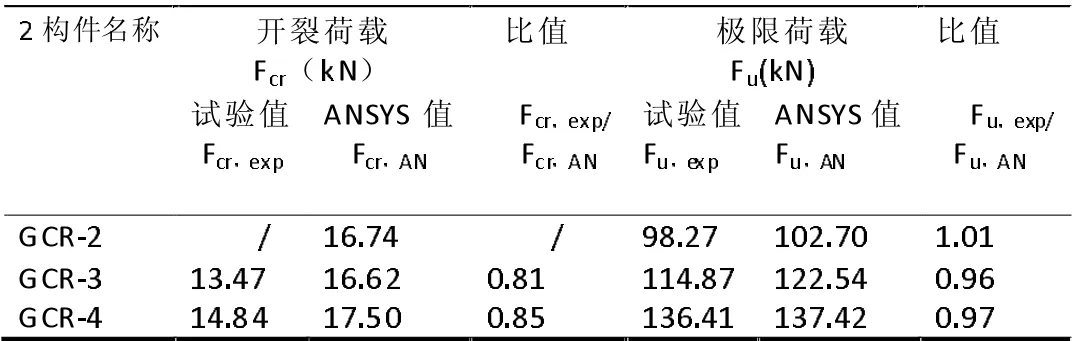
表2 开裂荷载和极限荷载比较

5 结论

综合以上分析，利用不考虑筋与混凝土滑移的分离式建模方法，用SOLID65 模拟混凝土、LINK8 模拟钢筋，ANSYS 软件对GFRP 加筋混凝土梁进行的非线性有限元分析，其结果是试验数据吻合较好。该建模方法能够应用于GFRP 梁的有限元分析中，能够较准确的反映GFRP 梁的受弯力学性能。