α- T3 晶格各向异性磁输运性质的研究

杜玉玲 杨荣森＊

（1、毕节市工业和信息化局，贵州 毕节551700 2、电子科技大学，四川 成都610054）

石墨烯因其高电导率、高迁移率等出色的导电性能，以及反常量子霍尔效应[1,2]、Klein 隧穿[3-5]而备受关注。石墨烯的出现使得二维材料成为广大学者研究的热点，在SrTiO3/SrIrO3/SrTiO3晶格的(111)方向生长三层结构[6]以及在冷原子限制下的光学晶格中[7]，研究发现了T3晶格，这种晶格的低能行为和石墨烯中的哈密顿量完全一致[8]。α-T3晶格最早出现在光晶格中，同时Hg1-xCdxTe 在二维极限和临界掺杂下，也能满足α-T3晶格模型[9]，作为一种介于石墨烯蜂巢晶格和T3dice 晶格的二维材料，参数α主要用来描述中央格点与蜂巢格点的耦合强度[10]。在α-T3晶格的大量研究中，已经发现Klein 隧穿效应[11,12]、Floquet 拓扑相变[13]、Hofstadter 蝴蝶效应[14]等物理性质。本文推导出α-T3晶格中粒子的透射概率表达式，并采用Mathematica 软件仿真，研究磁势垒下α-T3晶格的电子输运性质。

1 α-T3 晶格模型

α-T3晶格模型最初是针对冷原子系统提出的，是一种新型的二维材料。在α 取0 和1 的极限下，α-T3晶格分别对应于蜂巢晶格和T3晶格。如图1 所示，α-T3晶格的每个细胞包括三个格点，子格A 与子格B 耦合，跃迁振幅为t，子格C 只与子格B耦合，跃迁振幅为αt。

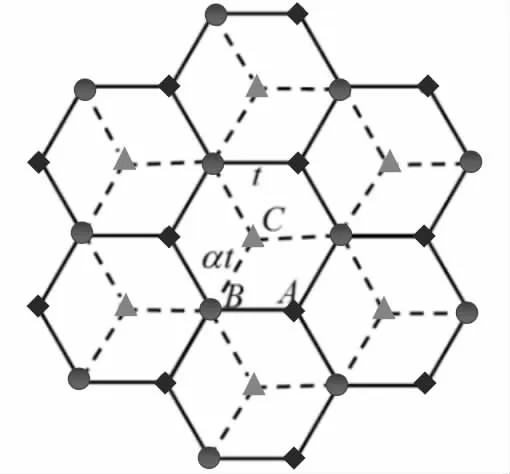
图1 α-T3 晶格模型

2 理论研究

假设α-T3晶格中的粒子从y-z 平面入射，粒子的入射角φ满足α=tanφ[11]，在宽度为L 区域II 上施加与x 轴方向呈角度θ的变化磁场M，磁化矢量在x-z 平面上，则α-T3晶格中低能电子的哈密顿量可以表示为[15]

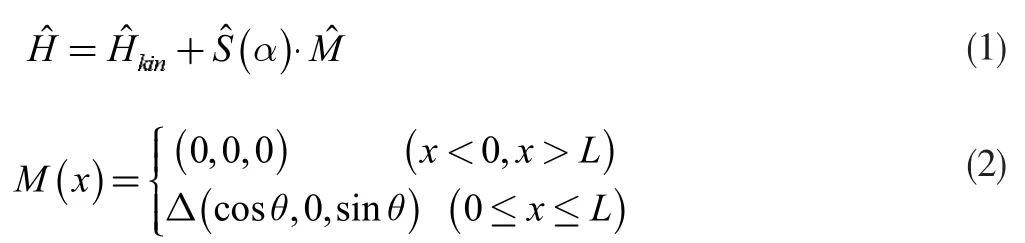
式（1）中，Hkin代表动能[10]，S(α)是α-T3晶格的矩阵，M(x)为施加的磁场，△是磁场强度大小，根据α-T3模型的边界条件[12]计算出各区域波函数。

在区域Ⅰ(x＜0)，有入射波和反射波：

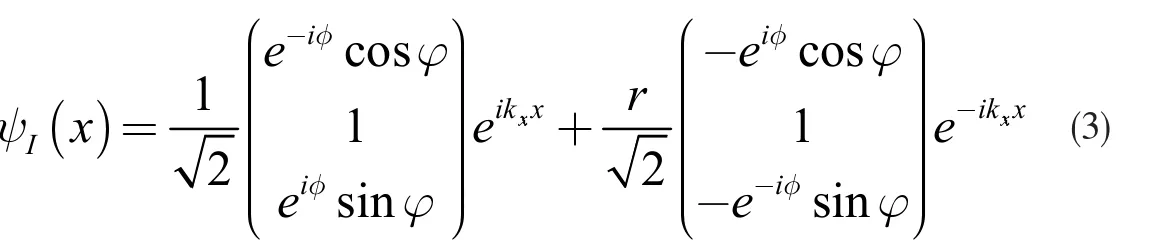
式（3）中，φ 是相位角，φ 是入射角，νF表示费米速度，r 是反射波的振幅，kF=E/νF是电子的三维波矢，无势垒区域波矢kx=kFcosφ。

在区域Ⅱ(0≤x≤L)，α-T3晶格处于磁场作用区域（磁场强度△=1），波函数如下：

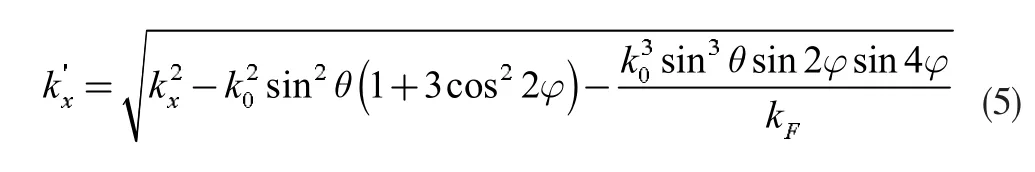
式（4）中，波函数主要由传播相反方向的两个波构成，振幅分别为a 和b，其中k0=△/νF，ky=kFsinφ。

在区域Ⅲ(x＞L)，有透射波：

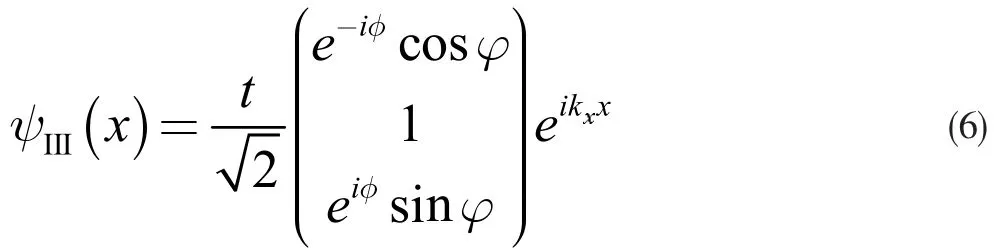
式（6）中，t 代表振幅。

通过x=0 和x=L 处的边界条件[12]，求得振幅参数a, b, r, t。最后，通过T=|t|2得到透射概率。

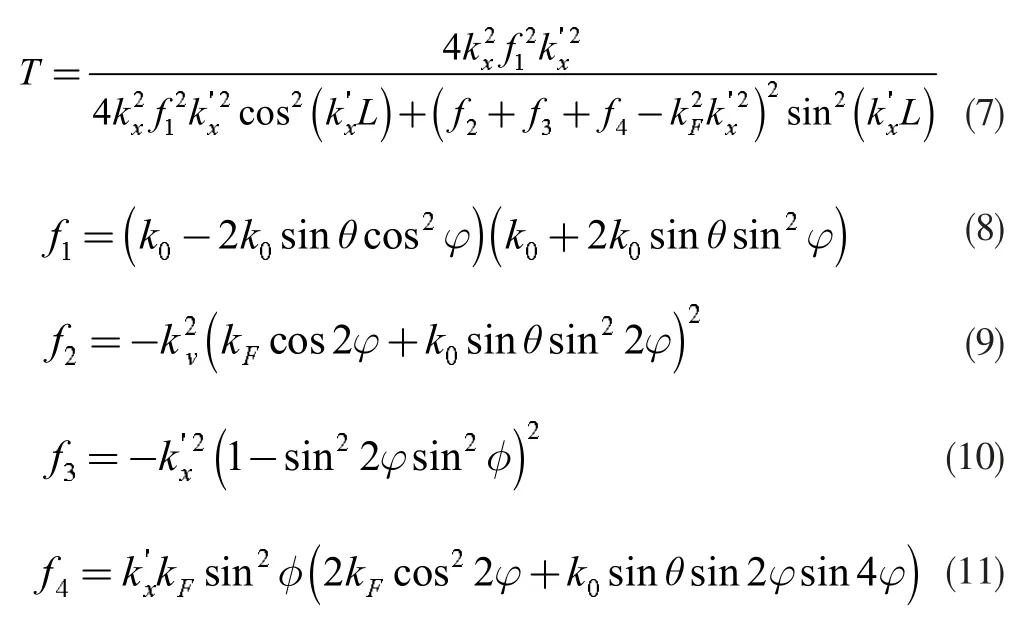
由式（7）可知，透射概率主要取决于磁化强度的z 分量，与x分量无关。当图2 中区域Ⅱ存在驻波时，入射波的透射概率T=1，满足k'xL=nπ（n 为正整数）的关系，与文献[12]结论相同。

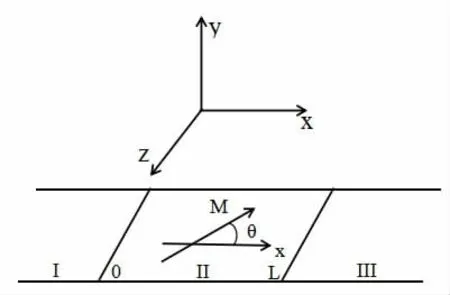
图2 磁场M 作用下的α-T3 晶格

对于α=0 的情况，蜂巢晶格的透射概率为

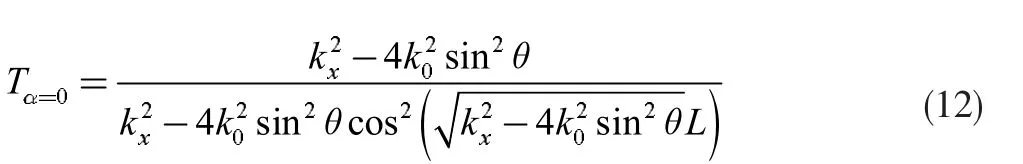
对于α=1 的情况，T3晶格的透射概率为

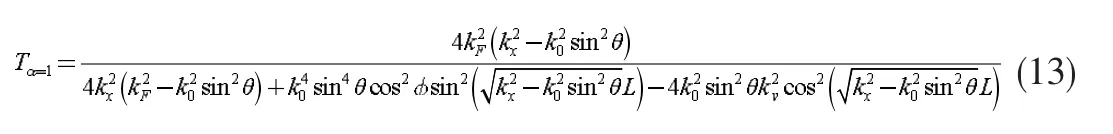
由式（12）和式（13）可知，在旋转角θ=nπ（n 取整数）的情况下，透射概率满足T(θ=nπ)=1，这种全透射现象表明了在没有赝自旋守恒下，石墨烯蜂巢晶格和T3dice 晶格发生后向散射。

根据Landauer-Büttiker 公式，发生隧穿的电荷电导可以表示为[11]

式（14）中G0=4e2kW/πh（W 是样品宽度，e 是电子电量的绝对值，k 表示波矢）

3 结果与讨论

图3 为透射率T 等高线图，其中，图3（a）中α=0，图3（b）中α=0.3，图3（c）中α=0.5，图3（d）中α=1, 参数kFL=5。当θ=nπ时，T(θ，φ)=1，α-T3晶格中的入射电子能够完全隧穿，没有反射电子，这与式（7）中T(θ=nπ)=1 结论一致。当磁场方向和x 方向平行时（即θ=nπ），对于所有的参数α (α=tanφ)，粒子的入射角度φ 不会对其透射造成影响。值得注意的是，当α 越大，粒子的透射区域也越大。如图3（a）和图3（d）所示，在石墨烯（α=0）和T3晶格（α=1）中，投射系数满足关系式T(θ)=T(θ+π)。当φ 的值确定，当θ∈(0,π/2]时，透射概率随着θ 的增大而减小；当θ∈(π/2,π)时，透射概率随着θ 的增大而增大；同时，在参数α=0.3 和α=0.5 情况下，θ∈[0,π]对应的透射区域小于θ∈[π,2π]对应的透射区域，这是因为透射率的解析式中不含磁场的x 分量，透射率仅由磁场的z 分量决定。

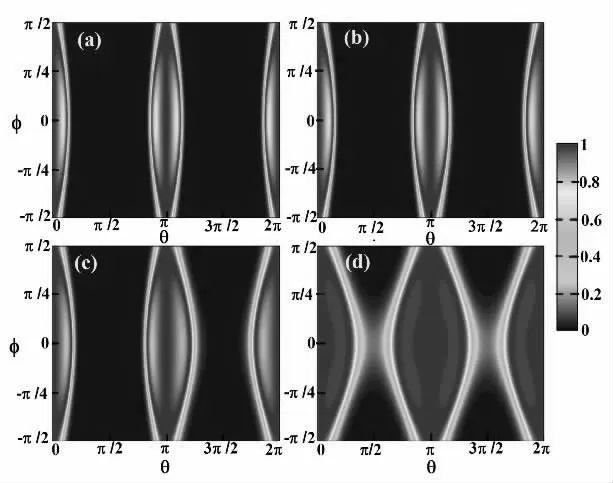
图3 透射率（T 作为θ，φ 的函数）等高线图

图4 为电导与旋转角θ 关系图，其中，图4（a）中α=0，图4（b）中α=0.3，图4（c）中α=0.5，图4（d）中α=1, 其中设置参数kFL=5。在旋转角θ=nπ（n 为整数）时，势垒“消失”，电导强度最大，电子发生全透射；而当旋转角θ=(n+1/2)π 时，电导率达到极小值。当入射能量E=0.5 时，存在两个临界旋转角θcrit使得电导为0，各向异性磁阻效应消失，这定义了电导为0 的电导间隙，这种现象使得α-T3晶格有望成为一个开关器件。值得关注的是，如图4（a）和图4（d）所示，当α=0 和α=1 时，G(θ)是周期为π 的周期函数，满足G(θ)=G(θ+nπ)，结论与文献[15]一致。

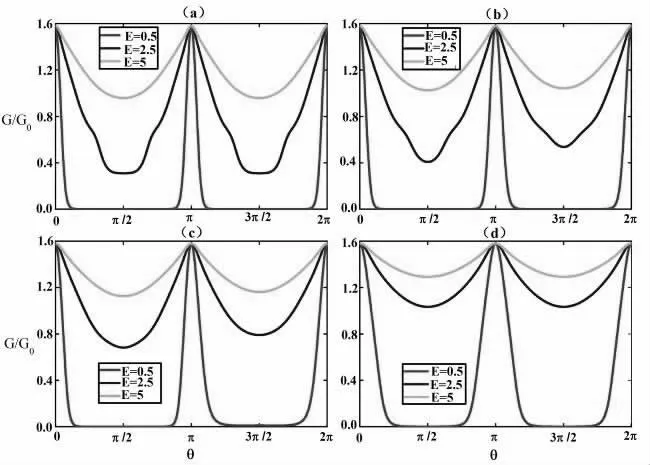
图4 电导与旋转角θ 的关系图

图5 为电导G 的等高线图，图5（a）中α=0，图5（b）中α=0.3，图5（c）中α=0.5，图5（d）中α=1, 设置势垒宽度参数L=5。在θ=nπ（n为整数）时，电导最大，这与图3 中无反射电子、发生完全隧穿的结论一致，电导与入射能量E 无关。在能量E 取定值的条件下，当θ∈(0,π/2]时，电导随着旋转角的增大而减弱；当θ∈(π/2,π) 时，电导随着旋转角的增大而增强；在旋转角θ 取定值的条件下，电导随着入射能量增大而增强。值得关注的是，在θ∈(π,2π)时，图5（b）和5（c）中，当能量取较小值时，电导不为0 甚至很大，这仍需进一步研究。

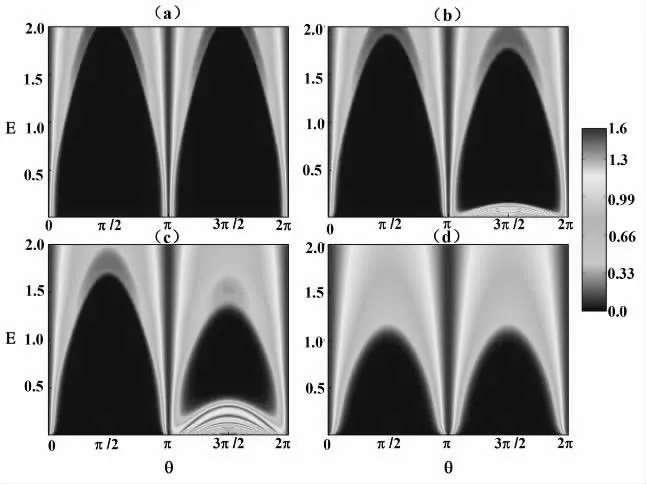
图5 电导G（电导作为E 和θ 的函数）等高线图

图6 为电导与入射能量的变化关系图，其中，图6（a）中α=0，图6（b）中α=0.5，图6（c）中α=1，设置势垒宽度参数L=5。当磁场方向和x 方向一致时，电导不会受到入射能量的影响，电子可以全部透射过去；而当磁场方向和x 方向垂直时，电导会受到入射能量的影响。由图6 可知，存在临界能量Ecrit，Ecrit随α 增大而减小。如图6（a）和6（c）所示，当E＜Ecrit时，电导为0，电子发生全反射；当E＞Ecrit时，电导随着入射能量E 的增大而增强。如图6（b）所示，对于α=0.5 的α-T3晶格，当θ=π/2，存在临界能量Ecrit使得电导为0，电子在小于这个入射能量时发生了全反射；当E＞Ecrit时，电导随着入射能量E 的增大而增强；当θ=3π/2 时，在入射能量很小时，存在电导波动峰值，出现振荡现象。

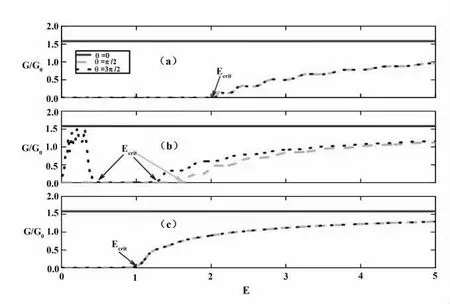
图6 电导与入射能量的变化关系图

4 结论

本文采用紧束缚模型，研究了α-T3晶格在施加变化磁场条件下的输运性质。研究发现，当磁场方向与x 方向平行时，α-T3晶格的电子能够完全穿过势垒，电导不会受到入射能量的影响。对于石墨烯(α=0)和T3晶格(α=1)两种极限情况，电导具有π的周期性，即G(θ+π)=G(θ)。对于耦合参数α 的中间值（0＜α＜1），电导不具有周期性。各向异性磁阻效应的产生依赖于入射电子能量，入射电子在一定能量范围内，入射粒子出现全反射，此时电导为0，各向异性磁阻效应消失。