温度与应力对破碎煤岩体压实变形特征的影响

张天军，刘 楠，庞明坤，张秀锋，王小军，张辛亥

（1.西安科技大学 理学院，陕西 西安710054；2.西安科技大学 安全科学与工程学院，陕西 西安710054）

我国煤矿煤自然发火非常严重，采空区自燃占发火总数的60%左右[1]。煤层开采后，上覆煤岩受采动影响下沉，破碎煤岩体发生压实变形形成采空区松散多孔介质[2－3]。褚廷湘等在文献[4]和文献[5]中提出采空区松散煤体自燃受应力场、温度场和渗流环境多场耦合的影响，其中渗透率和孔隙度是漏风流动的重要参数，对煤自燃过程有重要影响。所以系统的研究采空区遗煤在不同温度和应力下压实特性与渗透特性的变化规律，对于煤矿矿井火灾防治具有重要意义。

近年来，诸多学者在温度对煤岩体渗透特性影响和破碎煤体的压实特性方面做了大量卓有成效的研究工作。在煤体渗透率与温度和应力的关系研究中，众多学者通过实验研究的手段揭示了温度与应力对煤岩体渗透特性的影响规律。其中李志强[6]以标准型煤试样为研究对象，发现热应力大于有效应力时，渗透率随着温度的升高而增大，热应力小于有效应力时，渗透率随着温度的升高而减小；刘向君[7]得到随温度、围压升高，低渗透性砂岩孔隙度、渗透率都减小的规律；万志军[8－9]等人探究了温度和孔隙压力对岩石渗透率的影响规律，发现中长石细砂岩渗透率存在门槛值温度，当温度达到门槛值后，其渗透率出现大幅度增加；于永江[10]等通过研究了围压、轴向应力及温度对成型煤样渗透率的影响，揭示了随温度升高，煤样的渗透率呈降低趋势的规律。在破碎煤岩体的压实特性研究中，马占国[11]研究了颗粒大小对饱和破碎岩样压实特性的影响，并揭示了破碎岩石在压实过程中应力应变接近于指数函数关系的规律，但没有给出具体的本构关系；陈占清等[12]等通过饱和级配泥岩的压实变形试验研究得到了不同级配下试样轴向位移随轴向应力变化的曲线，并建立了一种饱和破碎泥岩压缩模量与轴向应力的关系式；冯梅梅[13]在连续级配的饱和破碎岩石压实特性研究中进一步揭示了Talbot指数对饱和破碎岩石压实特性的影响规律，并给出了考虑岩样级配的饱和破碎岩石压实本构模型。

之前学者们在温度对煤岩渗透特性变化规律方面和破碎煤体的压实特性研究方面做了大量的工作并取得了相应的成果，但较少有人研究不同温度下破碎煤体压实变形过程中渗透特性的变化规律。为此以破碎煤样为试验对象，通过自主设计的渗透系统以分级加载的方式对破碎煤样进行渗透试验，得到不同轴向应力和温度的条件下破碎煤体渗透特性及压实特性的变化规律。

1 试验设计

1.1 试验设备及试样

1）试验设备。试验使用自主设计、并获有专利权的破碎样渗透压实系统对破碎煤样进行渗流与压实试验，渗透压实系统示意图如图1。其主要包括DDL600电子万能试验机，渗透仪，电热装置，液压泵，电子秤以及计算机采集及控制系统。其中DDL600电子万能试验机在计算机控制系统的设定及控制下为渗透仪提供轴向压力，液压泵为渗透系统提供渗透压，计算机控制试验机及采集所需数据。此外还需要实验室恒温箱对破碎煤样进行加热养护。

图1 渗透压实系统示意图Fig.1 Schematic diagram of osmotic com paction system

2）试样制备。煤样取自西部某矿区，测得原煤密度为1 295 kg/m3，经破碎机粉碎，用分选筛分别筛选出5～10、10～15、15～20、20～25 mm 4种粒径的颗粒，各粒径区间的破碎煤样实物图如图2。因为同一粒径破碎煤样的渗透率在相同孔隙度下可能相差较大，而且粒径较小时，渗透率变化小，可能导致所要研究的实验规律不明显，所以将所筛选的4种粒径的破碎煤样按比例1∶1∶1∶1进行配比，根据渗透仪尺寸设定每组试样总质量为800 g，共5组，分别为煤样M－1、M－2、M－3、M－4、M－5。

图2 破碎煤样Fig.2 Broken coal sam ples

1.2 试验方法

破碎煤样一般采用稳态渗流法。在外力作用下，破碎煤样发生变形时，颗粒排列方式会发生相应的变化。带侧限缸筒中的破碎煤体在一定的应力作用下其颗粒间的排列方式将重新组建，使固体颗粒的空间排列和相关的孔隙分布发生相应的变化。所以试验采用轴向应力控制法研究破碎煤体在压实变形过程中的相关渗透特性。

试验采用分级加载方式，选取密度为874 kg/m3，动力黏度为1.96×10-2Pa·s的普通液压油为渗透液，分别设定3、4、5、6 MPa4级轴向应力，各级轴向应力加载时间均为120 s,保持时间均为15 min。每级轴向应力下分别设定0.5、1.0、1.5、2.0、2.5 MPa 5级渗透压进行渗流。试验步骤：将试样M-1放入实验室恒温箱中，在常压下进行升温加热处理。当达到其设定温度25℃时（M－2为50℃，M－3为75℃，M－4为100℃，M－5为125℃），保温均热3 h，再装入渗透仪带侧限的缸筒中，开启压力机，打开电热装置，升温至煤样对应温度，按照设置好的分级加载方式开始加载。记录每级轴向应力加载后的活塞高度变化，以此来计算试样的孔隙度。启动控制渗透压的液压泵，通过调节阀门，在每一级加载轴向应力下依次施加0.5、1、1.5、2、2.5 MPa的渗透压。称重记录每个渗透压梯度的流量，通过流量测定渗透率的大小。每完成1个试样的测定后，通过计算机数据采集系统得到其应力应变数据，然后换其它试样重复前面步骤，记录每组数据，直至试验完成。

2 试验结果

2.1 温度对渗透率的影响

渗透率是衡量渗透特性的重要指标，因此，研究破碎煤体在分级加载过程中的渗透率变化规律对实际工程有重要的指导意义。法国工程师达西在1855年通过大量的试验研究，于1856年正式提出著名的Darcy定律[14]：

式中：V为渗透速度（单位面积渗流平均流量）；K为渗透系数；J为水力坡降。

在Darcy流渗流理论中，认为流体的渗流速度和水力坡度成正比。渗透系数K，也称为水力传导系数，是渗流力学中的1个重要参数，它与渗透率的关系为：

式中：K为渗透系数；μ为流体的动力黏度；ρ为流体的质量密度。

在分级加载的各个时刻，根据记录的渗透液的流量可由式（3）计算出各级轴向应力和渗透压下的渗透率：

式中：Q为试样中水的流量，L；A为试样的截面积，mm2；L为试样的高度，mm；△p为试样两端的孔压差，MPa；m为渗透液的质量，kg。

采空区遗煤发生自燃时，将造成采空区温度场的改变，从而对破碎煤体的渗透性产生影响。为了得到温度对破碎煤体渗透率变化规律的影响，选取渗透压为1.5 MPa下的试验数据，得到各组破碎煤样渗透率随温度变化图（图3）。

图3 1.5 MPa渗透压下渗透率-温度变化Fig.3 Permeability-tem perature change at 1.5 MPa osmotic pressure

由图3可见，破碎煤体的渗透压随着温度的升高总体上是增大的。其中应力为4 MPa时，渗透率的变化趋势与其他应力条件下的变化趋势有所不同，虽然随着温度的升高呈波动变化趋势，但其总体上也呈上升趋势。在3 MPa轴向应力作用下，25℃对应的渗透率为9.125×10-5m2，125℃对应的渗透率为1.665×10-6m2，比25℃时上升了7.54×10-6m2。4、5、6 MPa下125℃对应的渗透率比25℃分别高了7.5×10-6、9.54×10-7、8.54×10-8m2。因为在采空区遗煤发生自然的过程中，随着温度的升高，煤体内部细观结构开始发生变化，煤体向外膨胀，同时破碎煤体的孔隙度增大，导致试样内部孔隙喉道变大，从而使破碎煤体的渗透率变大，渗透性变强。

2.2 温度对压实特性的影响

破碎煤体的孔隙度也是影响其渗透特性的1个主要参数。因此，研究破碎煤体在分级加载过程中孔隙度的变化规律具有重要的工程价值。随应力的增大，破碎岩样的孔隙结构发生了变化，在试验的各个时刻，根据采集到的轴向位移△h方可计算出岩样在每一时刻的即时孔隙度φ[14]：

式中：m1为缸筒中煤样的质量，kg；h为煤样的初始高度，m；ρ1为煤体的密度，kg/m3；△h为采集的轴向位移，m；A1为缸筒的横截面积，m2。

为了获得轴向压力与破碎煤体孔隙度的关系，根据试验数据分别得出各组破碎煤样孔隙度随轴向应力变化的曲线图（图4），不同温度下孔隙度φ与轴向应力p′拟合关系式见表1。

图4 孔隙度-轴向应力曲线Fig.4 Porosity-axial stress curves

由图4与表1可以看出，孔隙度随轴向应力的增加而减小，并且轴向应力越大，减小的越慢。在轴向应力由3 MPa到5 MPa时孔隙度快速减小，加载到5 MPa之后减小的速度逐渐变慢，总体上破碎煤样的孔隙度随着轴向应力的增大呈负指数非线性下降趋势。各组试样从3～6 MPa总体下降范围都在5%～6.2%，其中温度最高的M－5试样比温度最低的M－1试样总体上多下降了1.2%。

表1 孔隙度与轴向应力拟合关系式Table 1 Correlation between porosity and axial stress

采空区遗煤原本不具有承载能力，破碎煤体在上覆岩层重力以及地应力的作用下发生压实变形，孔隙度在压实变形过程中逐渐变小，压实度慢慢增大，从而恢复一部分承载能力。相同应力条件下，温度越高，孔隙度越大，在采空区遗煤自燃过程中，随着采空区温度升高，破碎煤体的堆积更为松散，导致孔隙度增大。

煤体破碎后相比比原来状态下的体积增大的特性成为煤体的碎胀性，通常用碎涨系数k0[13]表示：

式中：v1为煤岩破碎后的体积；v0为原始体积。

式中：m′为煤岩破碎前的质量；ρ′为岩心密度。

根据试验数据计算出每组试样的碎涨系数，选取4、5、6 MPa下的数据制出的碎涨系数－温度曲线图如图5。由图5可见，各个应力水平上的碎涨系数都随着温度的升高呈线性增长趋势，其中4 MPa应力水平下125℃对应的碎涨系数比25℃对应的碎涨系数增长了0.038，5、6 MPa应力水平下也分别增长了0.044和0.03。由此可见，碎涨系数具有较强的温度敏感性，在采空区遗煤自燃过程中，随着采空区温度升高，破碎煤体的碎胀系数逐渐增大，导致孔隙度增大、渗透率也将随之增大。

图5 碎涨系数-温度关系Fig.5 Crush factor-temperature relationship

2.3 破碎煤体的弹性模量

破碎煤体是地下煤体原有结构在采动应力与地应力作用下后发生破碎变形产生的，多见于采空区。破碎煤体在缺少周边约束时不具有承载能力，但其在围压及地应力作用后发生压实变形（塑性变形），又恢复了承载能力，此时不但具有可观的承载能力，还具有与完整煤体不同的力学性质。

破碎煤样在带侧限的缸筒中受侧向约束，只有轴向发生变形，产生轴向应变，所以其割线模量Es反映的是总应力应变的关系，计算公式为：

式中：σ为轴向应力，MPa；ε为轴向应变。

一般用切线模量Et来表示应力相对于应变的变化率，其公式为：

研究破碎煤体压实后的力学特性，整理并处理相关试验数据得到的各组破碎煤样的割线模量-应变曲线图如图6，切线模量-应变曲线曲线图如图7。

图6 割线模量-应变曲线Fig.6 Secantmodulus-strain curves

由图7可知，破碎煤样在压实变形过程中的割线模量与切线模量都随着应变的增大而增大，ES-ε和Et-ε关系都可以用指数函数较为准确地拟合，并且相关系数都在0.95以上。并且温度与割线模量的关系呈负相关性，相同的应变下，温度越高的煤样其割线模量的值越大。温度为25℃的煤样在应变为0.29时割线模量达到极大值22.1 MPa，此时温度为50、75、100、125℃煤样的割线模量分别为20.1、19、17.3、15.3。温度与切线模量的关系也呈负相关性，但温度为50℃与75℃的切线模量在应变为0.23之后相差较小。

图7 切线模量-应变曲线Fig.7 Tangentialmodulus-strain curves

2.4 本构关系的建立

马占国等[11]通过试验分析提出压实破碎煤体应力-应变函数关系式为：

式中：a、b为试验常数。

验证式（9）的可行性，根据试验数据得到的各组试样的σ-ε曲线图如图8。

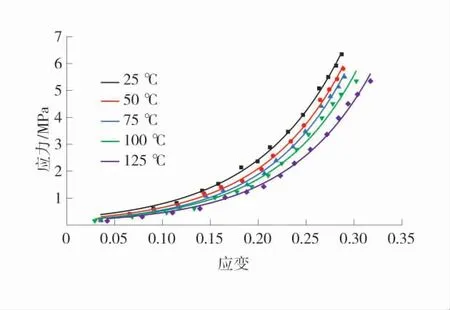
图8 应力-应变曲线Fig.8 Stress-strain curves

由图8可以看出，相同应力条件下，温度越高破碎煤体的应变越大，应力与温度呈负相关性。为了进一步探讨其影响规律，对在应力σi作用下破碎样的割线模量与温度的关系进行拟合，得到了考虑温度的压实破碎煤体的本构模型。

由式（5）可以推导出煤样在第i阶轴向应力作用下的割线模量Es公式为：

式中：i为第i阶轴向应力作用下的参数。

选取相关试验数据得到的破碎煤样的割线模量与温度的拟合关系式见表2。由图6和表2可以看出，不同应变条件下破碎煤样的割线模量ES均随着温度T的升高而减小。

表2 不同应变下割线模量与温度拟合关系式Table 2 The relationship between secantmodulus and temperature under different strain is fitted

用表2的线性关系式拟合相关系数达到0.95以上，线性关系式为：

式中：A、B为试验常数；T为温度，℃。

由式（11）可得，某一温度（T＝Tp）的破碎煤体在轴向应力σi下的割线模量为：Esp＝σi/εip＝A＋BTp，而另一温度（T＝Tq）的破碎煤体在相同轴向应力σi下的割线模量为：Esq＝σi/εiq＝A＋BTq，设Tp＞Tq。那么此时T＝Tp与T＝Tq的煤体的在轴向应力σi下的应变分别为εip与εiq。

由破碎煤体的压实特性可以得出，同一轴向应力条件下温度越高，破碎煤体的变形越大，所以T＝Tp与T＝Tq的破碎煤体的在轴向应力σi下的的变形差△Si为：

式中：△hip与△hiq分别为T＝Tp与T＝Tq时的破碎煤体的在轴向应力σi下的的变形量，m；h0p与h0q分别为破碎煤体在T＝Tp与T＝Tq时的初始高度。

通过对在应力σi作用下破碎样的割线模量与温度的关系式进行插值，得到了考虑温度的压实破碎煤体的本构模型为：

式中：A、B为试验参数，可由试验测出。

由式（13）可以看出在压实过程中，同一应变条件下温度T与应力σ的关系为一次线性关系，为验证所得本构模型的合理性，结合相关试验数据，根据式（13）算出应变分别为0.21、0.24、0.26、0.28时不同温度下的应力，试验结果与本构关系计算结果对比图如图9。

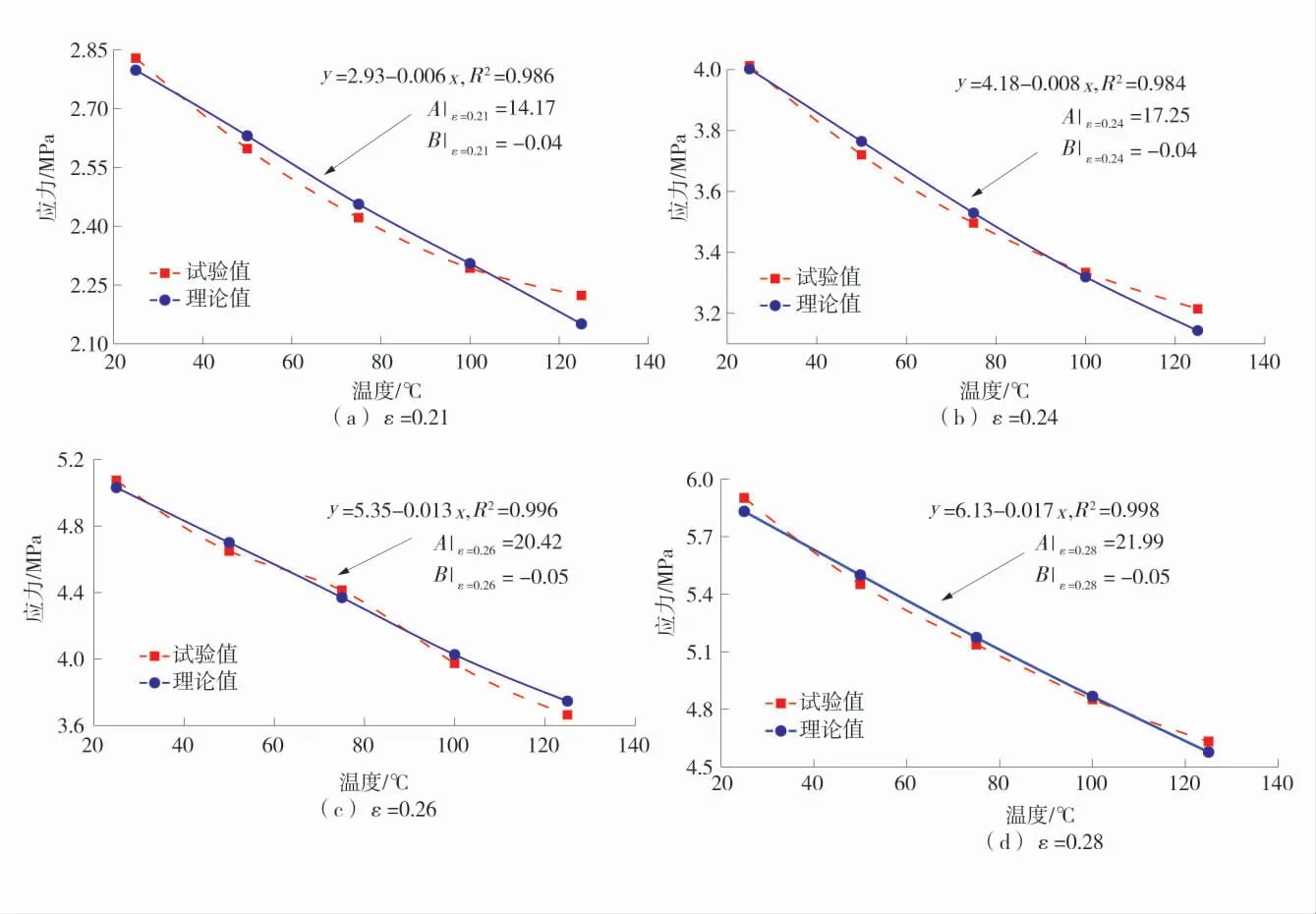
图9 试验结果与本构关系计算结果对比图Fig.9 Com parison between test results and constitutive relation calculation results

由图9可以看出，破碎煤样在4种不同应变条件下的应力随温度变化的理论曲线与试验曲线相关度均高于0.95，其中应变为0.28时的相关度高达0.99。由此可见，考虑温度的压实破碎煤体的本构模型计算结果与试验结果具有较高的一致性，从而验证了该本构模型的合理性与准确性。

3结论

1）渗透率随着温度的升高总体上呈增长趋势，相同的轴向应力下，125℃对应的渗透率比25℃对应的渗透率都有所升高。随着温度的升高，在热膨胀效应下煤体向外膨胀，破碎煤体孔隙吼道变大，从而导致渗透率增大。

2）在破碎煤体压实变形过程中，孔隙度随着轴向应力的增大而减小，承载能力也随着孔隙度的减小而增大，在轴向应力由3 MPa到4.5 MPa时孔隙度快速减小，加载到5 MPa之后减小的速度逐渐变慢，由此可见，破碎煤体的孔隙度具有较高的应力敏感度，且温度越高，压力敏感性越强。

3）相同应变条件下，破碎煤体在压实变形过程中的割线模量和切线模量均随着温度的升高而降低，两者与温度的关系曲线均可用关系式y=a ebx较为准确的拟合，相关系数均在0.95以上。

4）通过对在应力σi作用下破碎样的割线模量与温度的关系进行拟合，得到了考虑温度的压实破碎煤体的本构关系为：σi＝εip（A＋BTp）。并将试验数据带入本构关系式中，验证了其准确性与合理性。