基于峭度熵与分层极限学习机的动量轮轴承故障诊断研究

刘鹭航，张强，王虹，李刚，吴昊，王志鹏，郭宝柱,*，张激扬

1. 中国航天系统科学与工程研究院，北京 100037

2. 北京控制工程研究所，北京 100094

3. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044

航天器结构复杂化，技术、功能综合化，性能、工况多样化，耦合作用丰富化，导致航天器的故障发生频率增大,发生方式更具隐蔽性。卫星故障数据库统计数据表明，40%的卫星故障为姿态控制系统故障所致[1]，姿控系统的故障可能使卫星姿态丢失而引起重大事故。动量轮是姿态控制系统的关键部件，其可靠性直接关系到整星寿命与安全。动量轮的故障或失效可能导致卫星的整体失控。动量轮由驱动电机、轴承组件、轮体组件和壳体组件组成。其中，轴承组件是动量轮的核心组件和薄弱环节。由于动量轮处于长期运行中，这对轴承的可靠性提出了非常苛刻的要求。因此，动量轮轴承故障诊断技术具有重要的工程意义和研究价值[2-3]。

卫星工作环境恶劣，设备结构复杂精密，动量轮和姿控系统之间耦合关系复杂，动量轮轴承的监测信号往往混杂多种噪声，如何实现微弱故障的早期诊断成为研究的热点。马艳红等[4]提出了具有非均匀力学特征参数的动量轮微振动仿真模型；何田等[5]提出了轻载滚动轴承微弱耦合故障诊断的改进EEMD方法；刘红星等[6]将自适应共振解调应用于空间精密轴承保持架磨损故障诊断。然而这些方法依赖于轴承振动模型的精确程度，缺乏对低信噪比下微弱故障特征提取的环境适应性和抗干扰能力。为了克服这一问题，研究低信噪比下动量轮轴承弱故障特征提取与诊断十分必要。

近年来，非线性信号处理算法得到广泛的关注，成为旋转机械故障特征提取的研究热点之一[7]。变分模态分解(variational mode decomposition，VMD)可以将原始信号自适应地分解成多个本征模态函数，每个模态函数各有一个中心频率。VMD作为一种完全非递归的准正交方法，具有信号分解提取的独特优势。JIANG等[8]研究了变分模态分解(VMD)在轴承故障诊断中的应用，并提出了改进方法。试验证明，VMD的分解效果远超过小波分解、经验模态分解等方法。

此外，DWYER等[9]提出的谱峭度指标(spectral kurtosis，SK)可以有效表征信号的脉冲性如何随频率变化，并可以检测故障引起的冲击量(或突起)。ANTONI等[10]深入研究了这一概念，提出了快速谱峭度图法(fast kurtogram，FK)。该方法被证明在早期故障诊断领域具有显著的优势，并被应用于旋转机械的故障诊断之中[11-12]。然而，FK在面临较低信噪比时表现欠佳[13]，因此人们在此基础上又提出了Protrugram方法[14]。Protrugram方法利用信号包络谱幅值的峭度来计算谱峭度图，在低信噪比下能够比快速谱峭度图更有效地检测瞬态冲击，有效克服了低信噪比下的故障特征提取困难。然而，该方法的应用需要专家经验和人工干预来预先确定带宽和去除离散频谱(discrete tones)。考虑到动量轮的复杂耦合作用关系及恶劣工作环境，这些缺点限制了Protrugram方法在动量轮轴承故障诊断领域的应用。受到信息熵的启发，本文提出了一种新型特征提取方法：峭度熵。本文将变分模态分解VMD与峭度熵相结合，用于提取动量轮轴承振动信号的微弱故障特征。在故障识别部分，不同的故障识别方法影响精度和速度，而基于极限学习机(ELM)的故障识别方法已经验证了速度和精度上的优势[15]。因此，本文选用最新提出的分层极限学习机(hierarchical extreme learning machine，H-ELM)作为故障识别算法，并在文中使用动量轮轴承数据证明该方法相较于传统极限学习机的优越性。

1 方法与理论分析

本文使用VMD对动量轮轴承振动信号进行分解，将原始信号分解成多个本征模态函数，并在Protrugram方法的基础上，通过计算谱峭度的信息熵值来提取振动信号分解后本征模态函数的特征，避免Protrugram所需要的人工干预和带宽设定。该特征适用于动量轮轴承故障诊断算法中；使用H-ELM对峭度熵特征向量进行训练，并使用该模型对动量轮轴承的运行状态进行诊断。本文所提出研究方法的具体实现过程如图1所示。

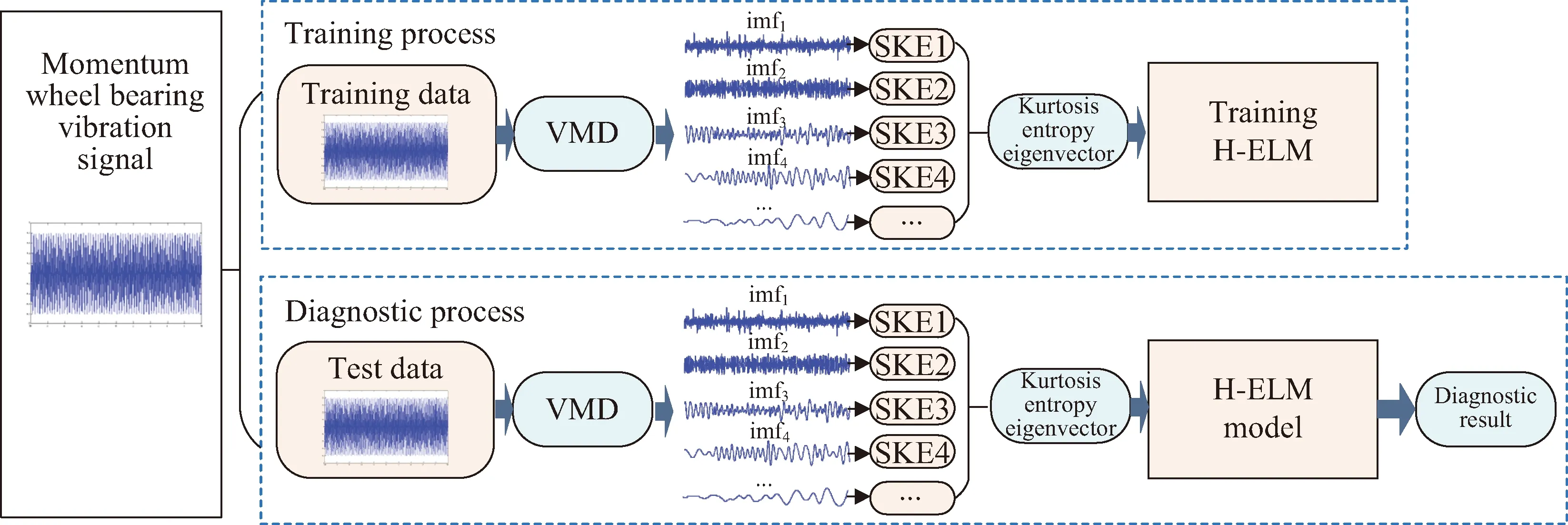
图1 方法的结构流程

1.1 变分模态分解

变分模态分解VMD是一种自适应信号分解新方法。变分模态分解假设信号由多个中心频率不同的模态函数叠加，其原理为:

式中：x为原始信号；imf为模态函数，也可写作{μk}={μ1，…，μK}；A为幅值；φ为相位。设有K个模态函数μk(t)，各模态函数对应的中心频率为ωk。引入拉格朗日算子λ，具体实现步骤如下:

2)执行循环：n=n+1；

3)分别更新μk，ωk，λ，

4)重复以上步骤，直到满足迭代停止条件

结束迭代，得到K个imf分量。

1.2 峭度熵

峭度是故障诊断领域常用的特征值，可以用来表征信号的冲击成分。其计算公式如下：

式中：X为原始信号，μ和σ分别为信号的均值和标准差。对于离散信号向量X={x1,x2,…,xN}，式(1)可以改写为：

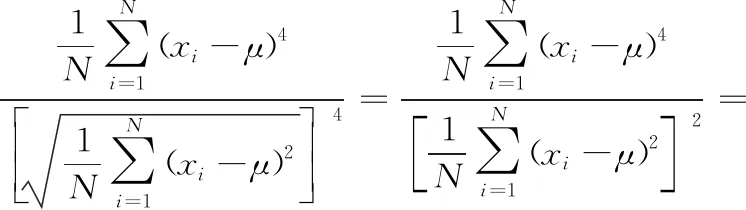
式中：N为信号长度。峭度已经广泛应用于机械故障诊断，但它是一种时域指标，无法实现精确的时频分析。

Protrugram方法基于峭度的概念，利用信号的窄带包络谱的振幅来计算谱峭度值。与FK相比，Protrugram需要预先确定带宽(BW)并寻求最佳中心频率(CF)。BW的设置主要取决于专业知识和先验知识。此外，附加的人工后处理对Protrugram也必不可少。针对这些缺点，并在可变条件下自动提取故障特征，本文利用香农熵理论提出了一种新的特征参数：峭度熵(spectral kurtosis entropy,SKE)，峭度熵的计算步骤如下。

1)基于变分模态分解得到的本征模态函数imf，应用快速傅里叶变换获取各个imf的频域分析结果；

2)设定分析的带宽和步长。通常带宽设定为故障本征频率的3～5倍。在本文的研究中，峭度熵对于参数设定不敏感；

3)中心频率设定从带宽的一半到采样频率的一半逐渐滑动，并确定相应的窗口；

4)应用快速傅里叶逆变换处理获取的窄带信号；

5)计算相应的窄带包络谱；

6)获取包络谱的峭度；

7)反复迭代步骤3)～6)，直至得到谱峭度向量SK={sk1,sk2,…,skF}；

8)根据峭度熵的定义，将峭度熵用下式表达，计算最终结果：

1.3 分层极限学习机

原始的多层极限学习机[15]是基于极限学习机的多级嵌套模式，可以通过指定数据的类型，自行调整神经网络的权值和阈值，从而实现无监督学习；同时，在调整权值和阈值时满足正交条件。本文使用的分层极值学习机改进了结构和ELM自动编码方法[16]，将整个网络划分为两个独立的子系统，替换使用特征提取结果的随机投影和惩罚因子，剔除正交约束限制，更好地处理并行性问题，其结构如图2所示。

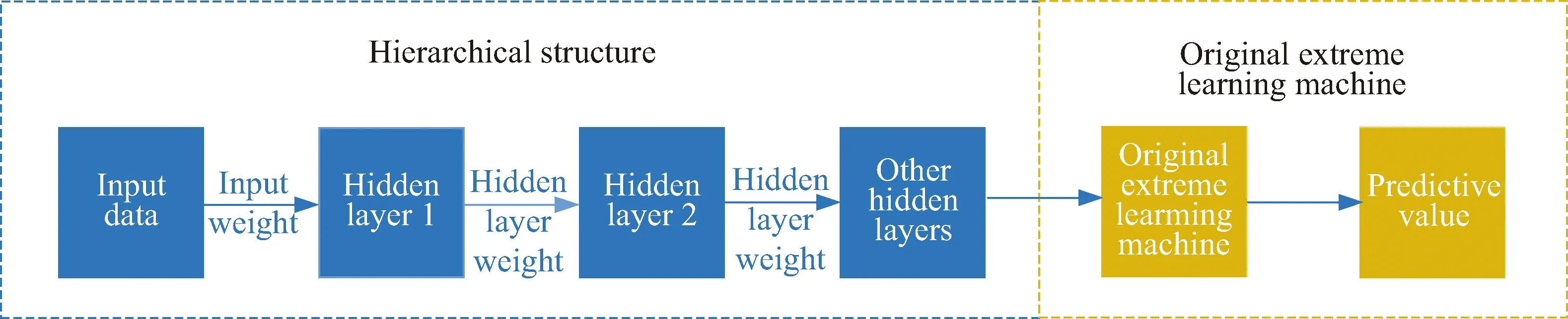
图2 分层极限学习机算法结构

H-ELM将输入的原始数据转换成一个随机特征空间，可以有效地挖掘训练样本间的隐藏信息。然后，对节点进行N层学习，获得高级稀疏特征，每个隐藏层的输出可以表示为：

Hi=g(Hi-1·β)

式中：Hi为每层的输出；g为激活函数；β为输出权值。

文中将改进后的稀疏自动编码器的优化模型总结为以下方程：

式中：Xf为输入数据；H为随机映射输出。

相较于原有的DL算法，不需要在迭代过程中进行调整，有助于提高训练速度以及学习的准确性[17]。

Oβ=p(β)+q(β)

式中：p(β)=‖Hβ-Xf‖2，q(β)=‖β‖l1为训练模式的惩罚期限，其中l1范数是向量中各元素绝对值之和。

在训练部分，依旧使用传统极限学习机的广义逆矩阵法，为了解决局部最优解问题，该算法不使用极限学习机的快速迭代收缩算法(FISTA)。

2 试验验证

为了充分验证算法的可行性和有效性，保证该算法能够应用在不同的场景下，首先用美国凯斯西储大学轴承数据中心的旋转机械故障诊断领域的经典数据集，对算法进行了可行性验证，保证算法能够在真实数据中得到理想的结果。然后再利用某型动量轮轴承试验台采集的实际数据进行试验验证。算法在两种场景下进行训练和验证，两种场景的数据类型相似，都包含正常和故障数据，可以验证算法的有效性。算法的有效性判定使用精确度，即分类结果的正确性。

2.1 滚动轴承试验验证

本文使用的轴承数据来自美国凯斯西储大学的公开网站。被测试轴承为SFK轴承，使用电火花加工技术在轴承上布置了单点故障，故障直径选取了1.78×10-4mm，转速为1 772 r/min。本文选取了采样频率12 kHz情况下的滚动轴承正常状态、内环故障、外环故障和滚动体故障共4种状态下的数据进行分析，每个状态选取120 000个测试点，一半作为训练数据，一半作为测试数据来进行验证。

首先计算所处理信号的频谱，如图3所示。中心频率和杂波总共为5个，因此要分解的模态数K应当大于5。

图3 轴承频谱

在测试后选取K值为6并代入VMD进行分解，结果如图4所示。

图4 VMD分解结果举例

为排除杂波干扰以及加快算法速度，本文仅选取由算法判定的权重占前四的imf构成特征矩阵。该部分并不使用传统的Hilbert矩阵进行构建，而是直接将数据按时间序列顺序代入矩阵，从而使特征矩阵尽可能多地保留数据特征。之后将特征矩阵输入SVD进行分解。根据分析，不同状态下特征值的大小差异显著，分解效果良好。

选取每个状态的峭度熵特征值输入分层极限学习机中进行训练并识别测试。经过试验发现，H-ELM在层数为3时表现效果良好，随后采用步进法调整神经网络各层的隐藏节点个数。对每个节点的个数进行循环训练，从10个到100个，找到最优解。根据测试，输入随机矩阵维数分别为200×12、200×30、200×35，输入激活函数为tribas时，循环测试精度为97.5%，单次训练时间为0.002 308 7 s，测试时间为0.000 788 23 s，可见训练结果良好，证明了该算法的有效性。

2.2 动量轮轴承试验

本文针对某型动量轮开展试验验证分析。该型动量轮的结构示意如图5所示，它的组成包括驱动电机、轴承组件、轮体组件和壳体组件。其中，轴承组件是动量轮的关键组件，轴承组件主要部件为上、下两个轴承，轴承为外圈旋转。轴承规格为B7004C，其外形尺寸为Φ20 mm×Φ42 mm×12 mm(内径×外径×宽度)，滚珠个数12颗，滚珠直径为6.0 mm，轴承节圆直径为31 mm，接触角为15°。

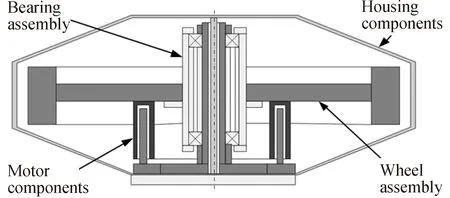
图5 动量轮结构

本次试验中，采用三向加速度传感器，采样率为25.6 kHz，测试过程中动量轮转速设定为4 600 r/min恒速运行。主要故障模式为轴承保持架磨损。正常及保持架磨损故障振动数据样本如图6、图7所示。对比可知，单以时域信号无法有效区分正常与故障数据，需要进一步频谱分析。

图6 动量轮正常数据样本

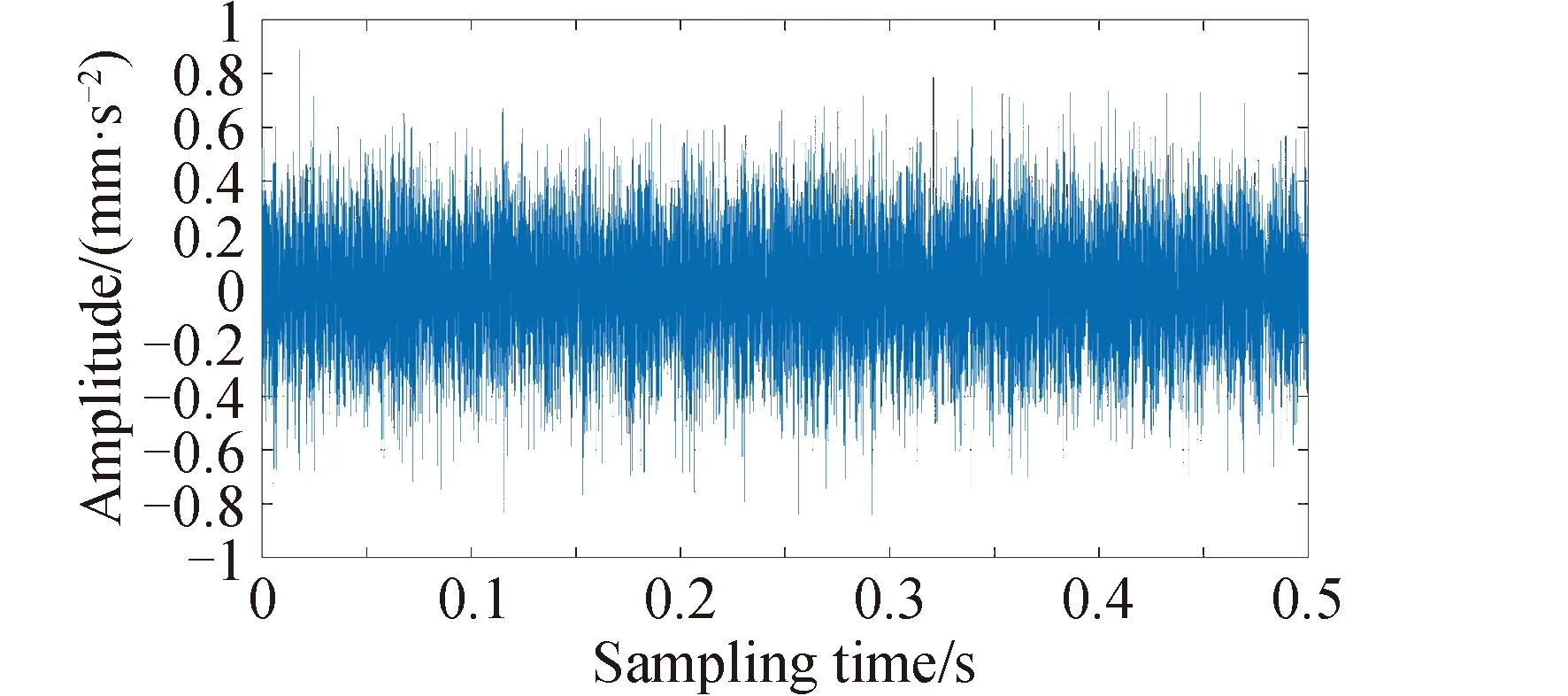
图7 动量轮保持架磨损故障时的数据样本

本试验与轴承试验步骤相同，首先画出频谱图，确定K值大小。在该部分设置模态数K为12，随后将该值与数据代入VMD进行特征提取。该部分依旧仅保留权重占前11的imf并按照时间序列顺序直接构建特征矩阵并代入峭度熵进行特征提取。频谱分析结果如图8所示，imf分解结果如图9所示。

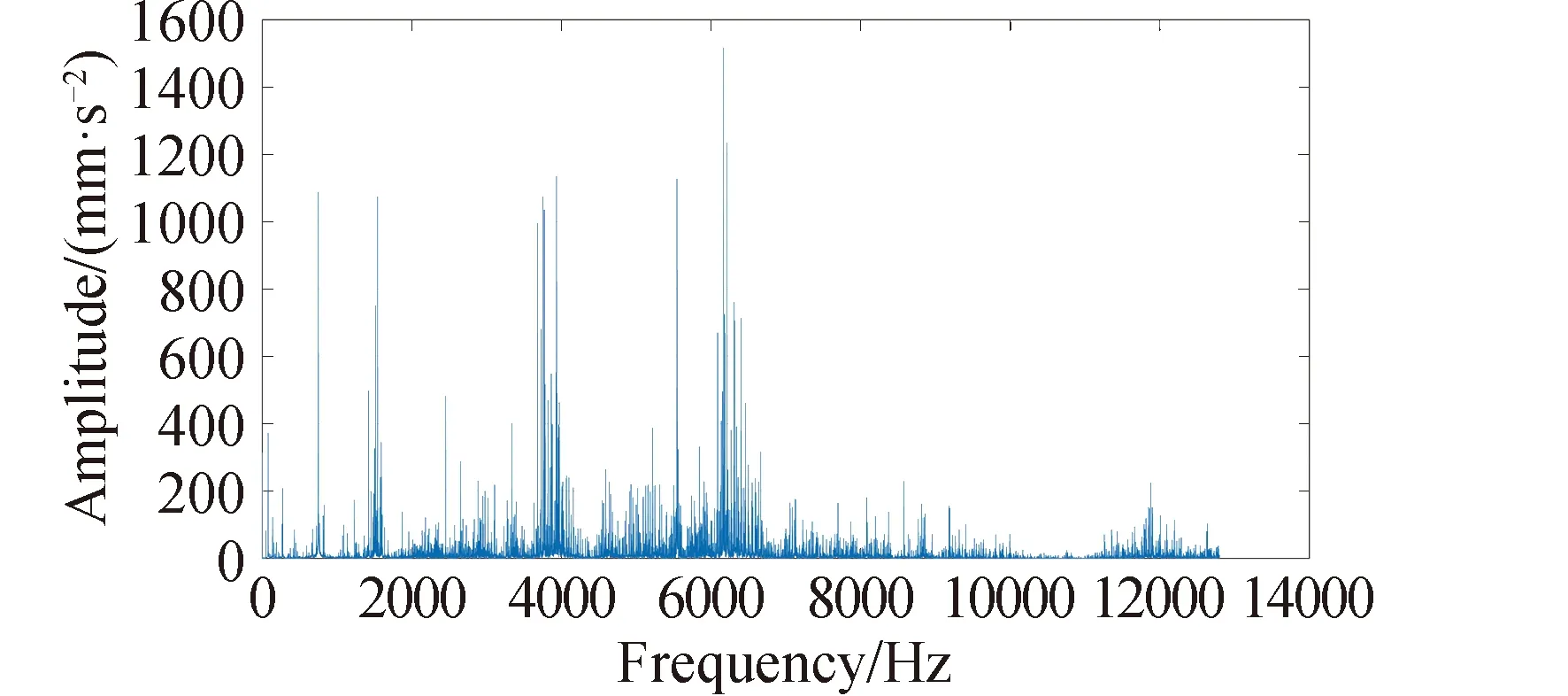
图8 动量轮轴承频谱

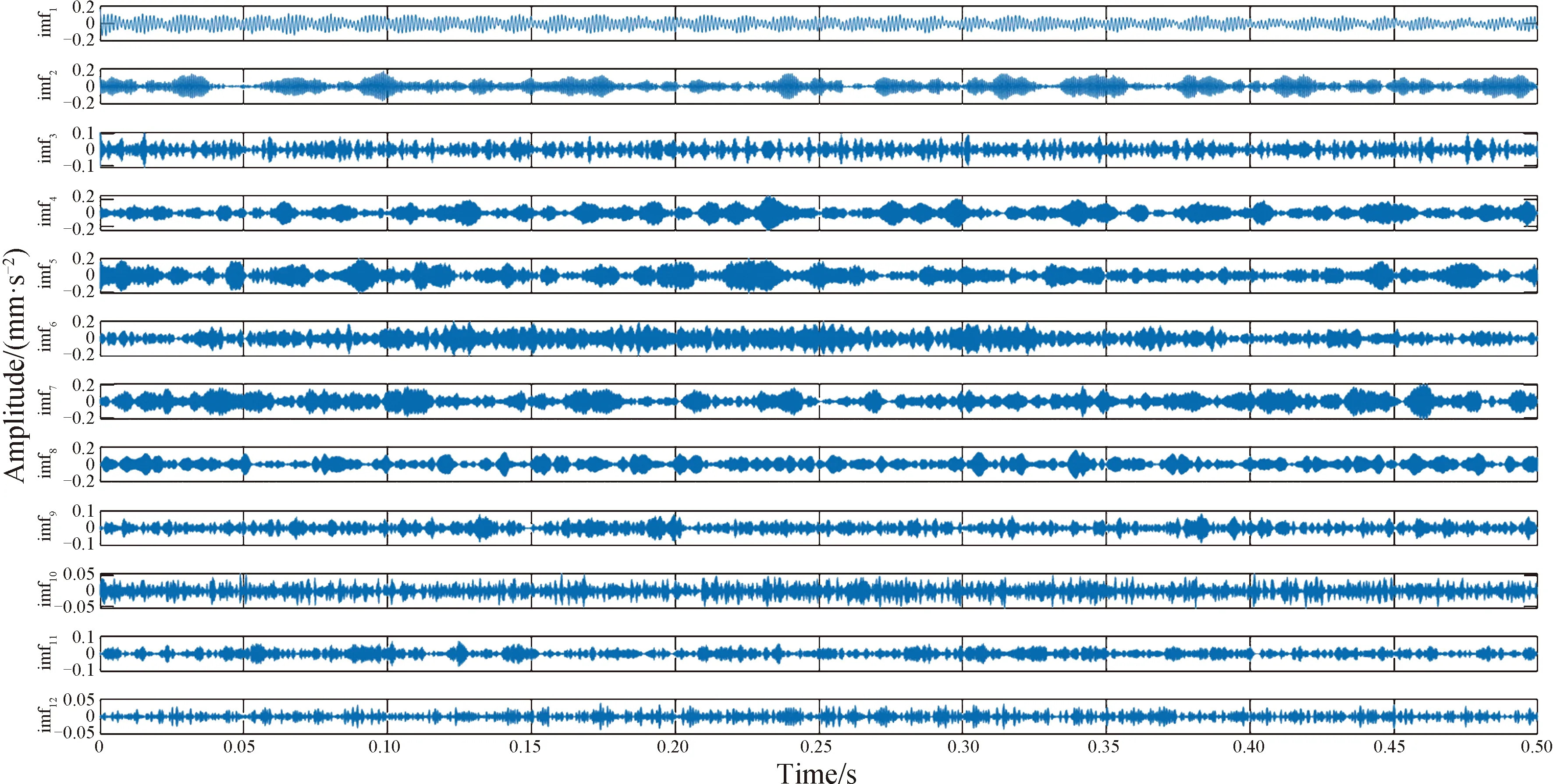
图9 分解结果样例

选取每个状态的峭度熵特征值输入分层极限学习机中进行训练并识别测试。该部分H-ELM的层数同样设置为3，使用步进法调参，在阵维数为400×57、400×24、400×23(即传统ELM中隐含节点数分别为57、24、23)，激活函数为tribas时循环精度为98.5%，单次训练时间为0.001 46 s，测试时间为0.002 35 s。在同等条件下，当分类器为ELM时，使用相同的数据，激活函数同样设置为tribas，在使用步进法调整隐含节点数目时，在节点数为167时获得测试精确度为96%，运行时间为0.014 2 s，故障诊断结果如表1所示。

表1 动量轮轴承故障诊断结果

从对比中可以看出，改进了结构和自动编码方法的分层极限学习机在应用于动量轮轴承故障诊断时，精度和速度皆优于传统的极限学习机。这证明了该方法在动量轮轴承的微弱故障诊断中的有效性和优越性。

3 结束语

本文面向耦合关系复杂的非线性信号特征提取进行了研究：1)研究基于VMD的信号分解方法，该算法自适应地将非线性信号分解成不同的IMF，解决了非线性信号模态混叠的问题；2)研究基于谱峭度熵的特征提取方法，在Protrugram方法的基础上，通过计算谱峭度的信息熵值来进行特征提取，从而避免了Protrugram所需要的人工干预和带宽设定，可成功应用于动量轮轴承故障诊断。结合VMD和峭度熵，可以获得单一算法难以获得的恶劣环境下动量轮轴承的弱特征数据。然后，利用改进了结构和ELM自动编码方法的H-ELM对动量轮轴承的特征数据进行训练，并在测试中达到了较高的分类精度，识别精度比使用ELM模型的分类精度更高。该算法准确识别了故障数据，表明该算法在多噪声混叠的情况下能够准确诊断出动量轮轴承的故障，可以实现真实运行情况下对动量轮轴承运行状态的实时监测，从而保证航天器的在轨安全运行。