涡旋压缩机传动系统的动静态特性研究*

2021-06-22王训杰

机电工程 2021年6期

薛丽,王训杰

(江西科技学院智能工程学院,江西南昌 330029)

0 引言

目前,涡旋压缩机已经被广泛应用于汽车和家用空调、发动机增压等行业。从其工作原理出发,要求涡旋压缩机的传动主轴采用偏心结构,动涡旋盘和传动主轴的质心不在同一回转中心线上,主轴受到离心惯性力以及气体力的作用,一般需要添加2个平衡块进行动平衡设计[1]。

为了研究主轴及其轴上零件组成的整体的动静力学特性,研究人员将主轴、动涡旋盘、2个平衡铁和皮带轮组成的一个整体,作为一个系统进行研究,简称为传动系统。通过对传动系统动静态性能进行研究,揭示了传动系统动静态特性与设计变量的内在关系,从而减小了动涡旋盘与静涡旋盘之间的摩擦,使动、静涡旋盘的啮合更加平稳有效,减小了轴承所承受的载荷,延长了轴承的使用寿命[2]。

传动系统动静态特性与其内部设计、外部运行参数关系紧密,尤其是与主轴的设计、轴承的型号、轴承跨距、主轴转速等参数的关系密切。文献[3,4]在假设主副轴承位置、主轴转速不变的情况,以平衡块的基本形状参数为设计变量,轴承承受的约束力为目标,完成了对传动系统动态平衡的仿真分析及优化设计;文献[5]在考虑了涡旋压缩机主轴转速变化的基础上,对其传动系统进行了多体动力学分析,得到了主轴曲柄销受力载荷和主副轴承受力载荷,并对曲轴系统在变载荷情况下的变形和应力状态进行了分析;文献[6]针对电主轴系统建立了三维有限元建模,通过对有限元模型的计算分析,获得了电主轴的模态和谐响应特性。

但是以上现有的研究尚未将涡旋压缩机动、静态特性结合在一起考虑,因此,其研究尚存在着一定的局限性和不足。

针对上述不足之处,在已有研究的基础上,笔者以主副轴承的刚度、布局位置、主轴转速及2个平衡铁的结构参数为设计变量,选取反映传动系统静动态特性参数的研究目标开展研究,分析设计变量对涡旋压缩机动静态性能的灵敏度,得到动、静态性能的主效应,为系统的结构优化设计提供借鉴。

1 传动系统动静态特性分析模型

1.1 参数化三维模型

建立传动系统参数化模型是分析系统动静特性的基础。笔者利用Pro/E软件参数化建模的特点,依据产品经验设计建立了三维模型。考虑到影响其动静特性的参数较多,因此在保证2个平衡块外形基本不变的情况下,笔者选取影响平衡块质量和质心位置较大的参数作为其设计变量。

笔者选取的传动系统模型及设计变量参数如图1所示。

图1 传动系统模型及设计变量

同时,笔者在考虑传动系统结构尺寸及装配关系的基础上,确定了各个设计变量的具体取值范围,如表1所示。

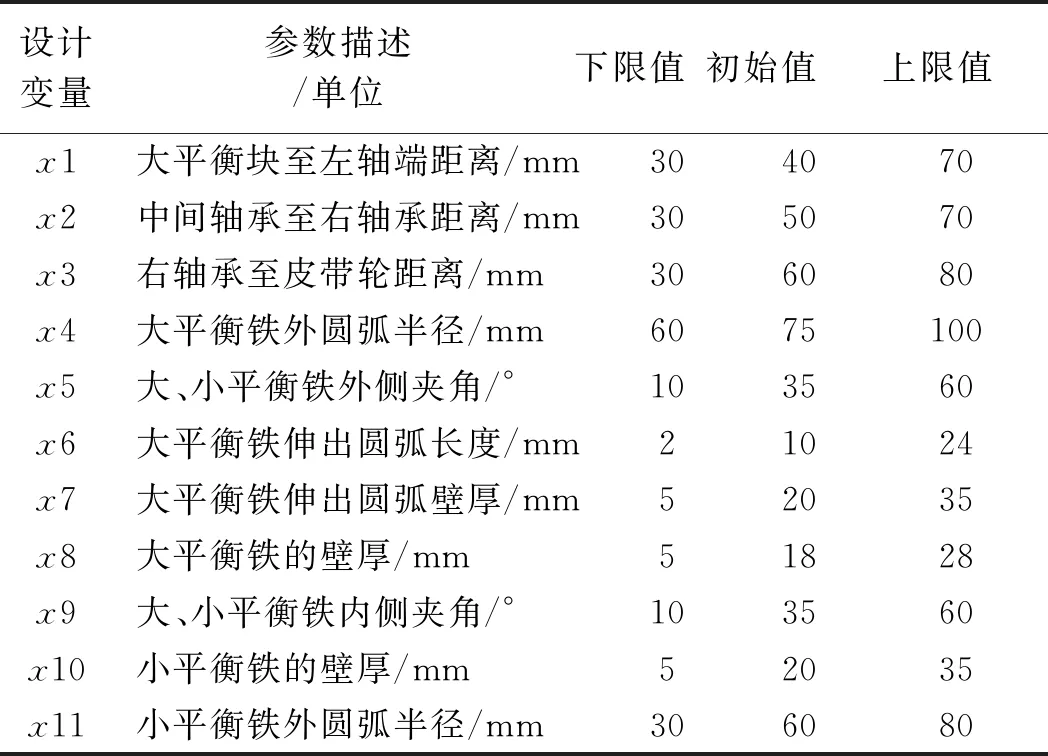
表1 设计变量及描述

1.2 有限元分析模型

动力学分析方法中,主要有传递矩阵法、有限元法、子结构法等,而其中又以有限元法应用最为广泛。

笔者在对某型涡旋压缩机传动系统进行建模和装配后,基于有限元法建立其离散化模型,为后续动静态特性分析做准备。

笔者采用Pro/E软件,按实际尺寸建立涡旋压缩机传动系统的三维模型,通过x_t格式导入Ansys WorkBench软件,然后定义材料的弹性模量、泊松比和密度。为了提高计算效率,便于对有限元模型进行分析,笔者对模型进行必要的简化处理,主要包括动涡旋盘用等效质量替代及忽略细节结构,如倒角、螺纹、退刀槽、圆角等局部特征;

合理地设置轴承刚度,有利于提高主轴系统的静刚度和动刚度,因此,笔者忽略交叉刚度和交叉阻尼参量的影响,将轴承1和轴承2对轴颈的支撑视为弹性支撑[7];不考虑轴承承受的载荷和回转时轴承刚度变化等因素,视轴承刚度为定值,且轴承只承受径向力,将其视为只承受径向力的弹簧质量单元处理;设径向刚度分别为k1、k2,在网格尺寸设置中将关联中心设置为密网格,设置单元尺寸为4 mm,采用四面体网格进行划分。

传动系统有限元网格模型如图2所示。

图2 传动系统有限元模型

2 传动系统静态特性分析

要对涡旋压缩机传动系统进行静态特性分析,主要考虑传动系统在气体力的作用下系统的变形情况[8];系统的变形越小,则表示传动系统的静刚性越好。

涡旋压缩机传动系统承受切向气体力Ft、径向气体力Fr和轴向气体力Fa的作用,大小平衡块产生的离心力Fdc和Fxc,3个轴承承受的力Fzzc、Fzjzc和Fyzc[9]。

考虑轴向气体力的平衡,可以通过开设背压孔来实现,笔者将实例Ft=1 001.70 N,Fr=101.39 N,作为工作载荷施加在曲轴偏心段的中间位置(如图1所示)。

为了分析轴承刚度对传动系统静变形的影响,笔者取径向刚度k1、k2的范围为5.7×106N/m～5.7×1010N/m,以传动系统的传动系统最大径向刚度为研究目标,采用超优拉丁方算法开展试验。

试验得到设计变量对最大静变形的主效应,如图3所示。

图3 设计变量对最大静变形的主效应

由图3可知:系统最大静变形随设计变量x1的增大而增大,随x2、x3、k1、k2的增大而减小;轴承1的径向刚度对传动系统的刚度影响较大,随着轴承1径向刚度的提高,主轴系统最大静变形减小,传动系统刚度提高;轴承2对传动系统影响较小。

因此,降低动涡旋盘的高度或减少偏心轴段的长度,均有助于缩短轴段x1的长度,提高传动系统的刚度。而通过调节轴承1支承及预紧以提高其刚度,对提高传动系统的静态性能具有十分重要的意义。

3 传动系统动态特性分析

3.1 传动系统模态分析

众所周知模态分析是动力学分析的基础,因此,通过模态分析可以掌握传动系统的振动特性,确定其固有频率、振型及位移变形等参数[10]。

其有限元动力学方程为:

[M]{X"}+[C]{X′}+[K]{X}={F(t)}

(1)

式中:[M]—质量矩阵;[C]—阻尼矩阵;[K]—刚度矩阵;{X}—位移矩阵;{F(t)}—力矢量。

在不考虑阻尼的情况下,笔者对其传动系统开展模态分析。

因[C]=0;[K]=0,则式(1)可以简化为:

[M]{X"}+[K]{X}=0

(2)

当其结构自由振动为简谐振动时,x=xsin(wt),自振频率为fi=vi/(2π)。

取表1的设计变量范围,笔者分析了设计变量对一阶响应频率的主效应,其分析结果如图4所示。

图4 一阶响应频率的主效应

由图4可以看出:传动系统的一阶固有频率随着轴承1的刚度k1增加而增加,转速的增加而减小;随着结构参数的增加,其一阶固有频率先减小后增大;轴承1的刚度k1对动态特性影响大的设计参数,对静态特性的影响也比较大。

由图4还可知:设计实例一阶响应频率103 Hz～114 Hz之间,随着阶数的增加,固有频率相应地增大;当工作最高频率超过114 Hz,传动系统本身结构,包括主副轴承相对位置、平衡块的结构等参数,对传动系统的固有频率影响很小。

因此,提高一阶响应频率的最好办法是通过调整主轴承刚度k1来实现。

一般情况下,要求传动系统的工作频率f<0.75fi(其中:fi—传动系统的第i阶临界频率),但考虑到变频涡旋压缩机工作的安全性,笔者确定其工作频率为77 Hz以下[11],实例一阶响应频率显然高于设计要求最大值。

3.2 传动系统谐响应分析

通过谐响应分析,可以得到结构在谐载荷作用下参考点幅相特性曲线,从而预测结构的持续动力特性,验证设计是否能克服共振,以及其他受迫振动引起的有害效果[12]。

以工作转速下传动系统的离心力作用为初始条件,为研究传动系统存在不平衡时,转子通过轴承传递的振动情况,此处假设主轴安装了2个平衡块(平衡块的形状和设计变量如图1所示),不同的设计变量产生不同的偏心质量,从而传递不同振动载荷至传递系统。

考虑到转子的结构、振型及支承的特点,此处振动测点尽量以工程实际为参考,设置4个测试点,具体布置如图1所示。

笔者分析低于一阶临界转速4个测试点振幅主效应,如图5所示。

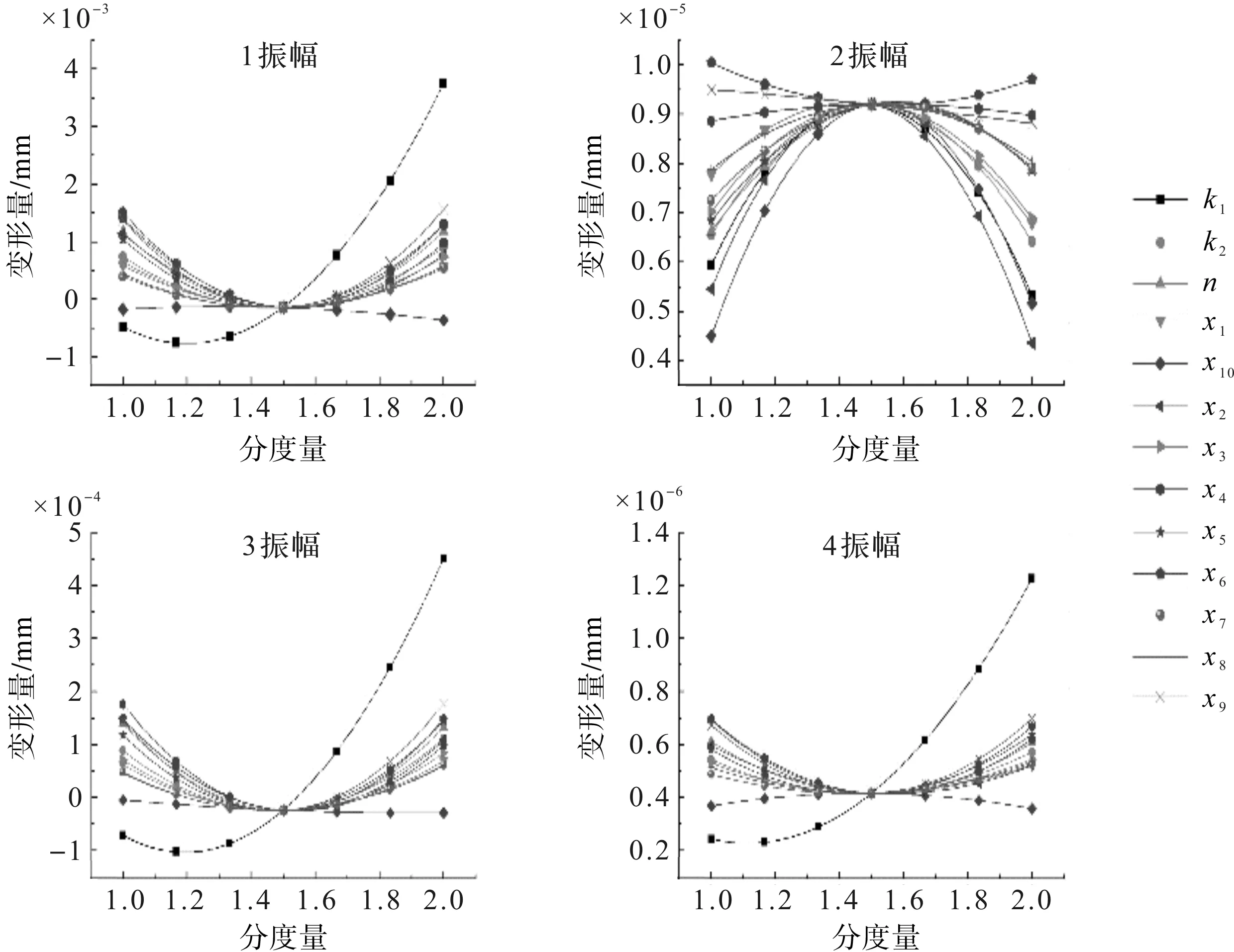
图5 4个测试点振幅主效应

由图5可以看出:系统在低于一阶临界转速下工作时,测试点1的不平衡幅值响应较大,测试点2的不平衡响应幅值较小;设计变量与不平衡幅值响应存在非线性关系,设计变量对不同测试点具有不同的响应,如测试点1、3、4不平衡幅值响应随刚度k1的增大而增大,而测试点2不平衡幅值响应随刚度k1的增大呈现先减小后增大的趋势;主副轴承相对位置和平衡铁的结构参数对振动幅值响应大于模态频率响应。