基于镜像对称补偿技术的脱皮机转子结构优化研究*

赵知辛,薛旭东,薛琳婧,潘晓阳,黄鸣远,李托雷

(1.陕西理工大学 机械工程学院,陕西 汉中 723000; 2.陕西铁路工程职业技术学院 高铁工程学院,陕西 渭南 714000)

0 引 言

以FBPY型脱皮机为基础,某企业进一步研发出了FBGY型双筒式谷物脱皮机。FBGY型脱皮机在兼顾FBPY型脱皮机优点的同时,进一步提升了脱皮效率,但因离心载荷而引起的脱皮机转子径向膨胀变形的问题,仍未得到有效的解决方案。当脱皮机转子发生径向膨胀变形时,会导致原有的谷物颗粒流通道变窄,造成加工质量、处理能力下降、导致颗粒流积聚、脱皮过程温升过高,影响产品风味物质及营养[1]。

结构补偿技术现已广泛应用于各个工程领域,尤其是涉及到高精度要求的三航领域时,结构补偿技术的应用更为广泛[2-4]。陈蔚芳等[5]提出了采用多次走刀时,采用分层补偿—优化补偿两种补偿方法,建立了优化加工优化补偿路径,以补偿薄壁件在加工过程当中因受力而引起的结构变形。

当考虑到加工变形与切削力的耦合作用时,研究人员采用迭代算法对优化模型进行了求解。雷宇等[6]以超重型卧式车床尾座套筒为研究对象,采用柔性化结构补偿,以多点碟簧结构代替传统的螺栓螺母结构,依靠碟簧的预变形量,来补偿因热变形和高额动态冲击载荷引起的尾座套筒变形。刘醒彦等[7]以典型航空零件为研究对象,提出了一种多工艺融合的结构补偿方法,并采用有限元方法建立了零件的有限元模型,采用PEPR算法对代理模型进行了求解,并且得出结论,即毛坯预变形与加工位置优化对控制零件加工变形是有效可行的。何涛等[8]以光栅线位移传感器校准装置为补偿对象,考虑到因温度影响,对其进行了热变形误差补偿,经热变形结构误差补偿,传感器能够很好地满足测量技术指标,能够为后续传感器的改进及研发提供一定的理论指导。BAZILEVS Y[9]以海上10 MW功率风力发电机叶片为研究对象,经有限元计算与海上平台试验,认为结构补偿技术能够有效地补偿风力机叶片在风载荷及离心载荷耦合作用下的变形,能有效保证风力发电机的发电效率。

热变形是制约高精度切削的瓶颈问题,一般的热变形补偿通常采用变形曲线来对结构进行补偿。VYROUBAL J[10]提出了一种分解分析的热变形补偿方法,采用保持架测量法,及时地对主轴、主轴箱的变形实施变形补偿。该方法可以极大程度上改善机器的残余热变形。对于高精度零件而言,变形补偿技术的应用已经十分成熟,但就在农业机械领域的应用而言还比较欠缺。

综上所述,对机械结构进行变形补偿是有效可行的,本研究针对脱皮机转子受离心载荷而引起的径向膨胀变形,采用结构补偿技术来进行解决。

1 谷物脱皮机结构及原理

1.1 脱皮机结构

该型脱皮机为双筒式脱皮机,其处理能力为24 t/h～25 t/h,由4台15 kW的电动机拖动,其具体结构如图1所示。

图1 脱皮机结构示意图1—电机;2—皮带轮;3—主轴;4—进料口;5—机身;6—外筒;7—颗粒流通道;8—转子;9—螺钉;10—八方盘;11—风机;12—出料口

1.2 脱皮机工作原理

该脱皮机在工作时,谷物受脱皮机转子作用,获得离心力,使谷物颗粒占据脱皮机内壁与转子外壁之间的颗粒流通道;转子纵梁上分布有数目若干的楔形独立搓皮板,搓皮板所设计的楔形几何结构用以实现谷物的旋转渐压旋剥脱皮,搓皮板在转子纵梁表面沿螺旋线布置提供谷物颗粒轴向所需的螺旋推动力,推进谷物前进;同时,利用搓板与外壁之间的揉压磨搓对谷物颗粒表皮进行剥离,完成脱皮后,利用悬挂风机提供的风力将麸皮与谷物形成的流化物进行分离,完成脱皮过程[11]。

2 脱皮机转子的有限元计算

结合脱皮机转子的实际参数建立脱机转子的有限元模型如图2所示。

图2 转子三维模型

在建立转子的三维模型时,为了能准确分析转子在受载条件下的一系列变化,本文采用三维单元体建模。为保证模型快速、准确的迭代求解,以及实现模型良好的参数化,本文采用ANSYS中的design modeler模块进行建模。笔者采用solid185单元对结构进行网格划分,只释放转子绕Z方向的旋转自由度,并对转子施加旋转速度。为保证后续迭代计算的效率及质量,笔者将搓板结构抑制,并以均布质量进行等效代替。

脱皮机转子主要部件材料属性如表1所示。

表1 材料属性

脱皮机转子的最大变形量计算结果如图3所示。

图3 转子变形云图

图3中,转子最大变形量为3.618 mm,最大变形位置处于两支距中间位置;变形分布趋势与实际情况相符。

转子应力分布如图4所示。

图4 转子应力分布云图

图4中,转子最大应力为167.38 MPa,与Q235A的屈服极限235 MPa仍有一定差值,表明结构仍具有一定的优化空间。

笔者使用Matlab对转子纵梁的变形分布数据进行拟合,其结果如图5所示。

图5 转子纵梁变形拟合曲线

图5中,转子最大变形位于沿纵梁长度方向的1/2处。

3 脱皮机转子的变形补偿

对于处理变形补偿求最优解的实际工程问题,可引入最优化设计模型对其进行约束。对于传统的优化路径,求解一般采用有限元直接求解法,但直接求解法耗时长、效率低、迭代步数多,且由于计算规模限制,样本点水平差异大。李重华等[12]提出了一种两步式优化策略,可很好适用于优化问题的求解,其求解思路如图6所示。

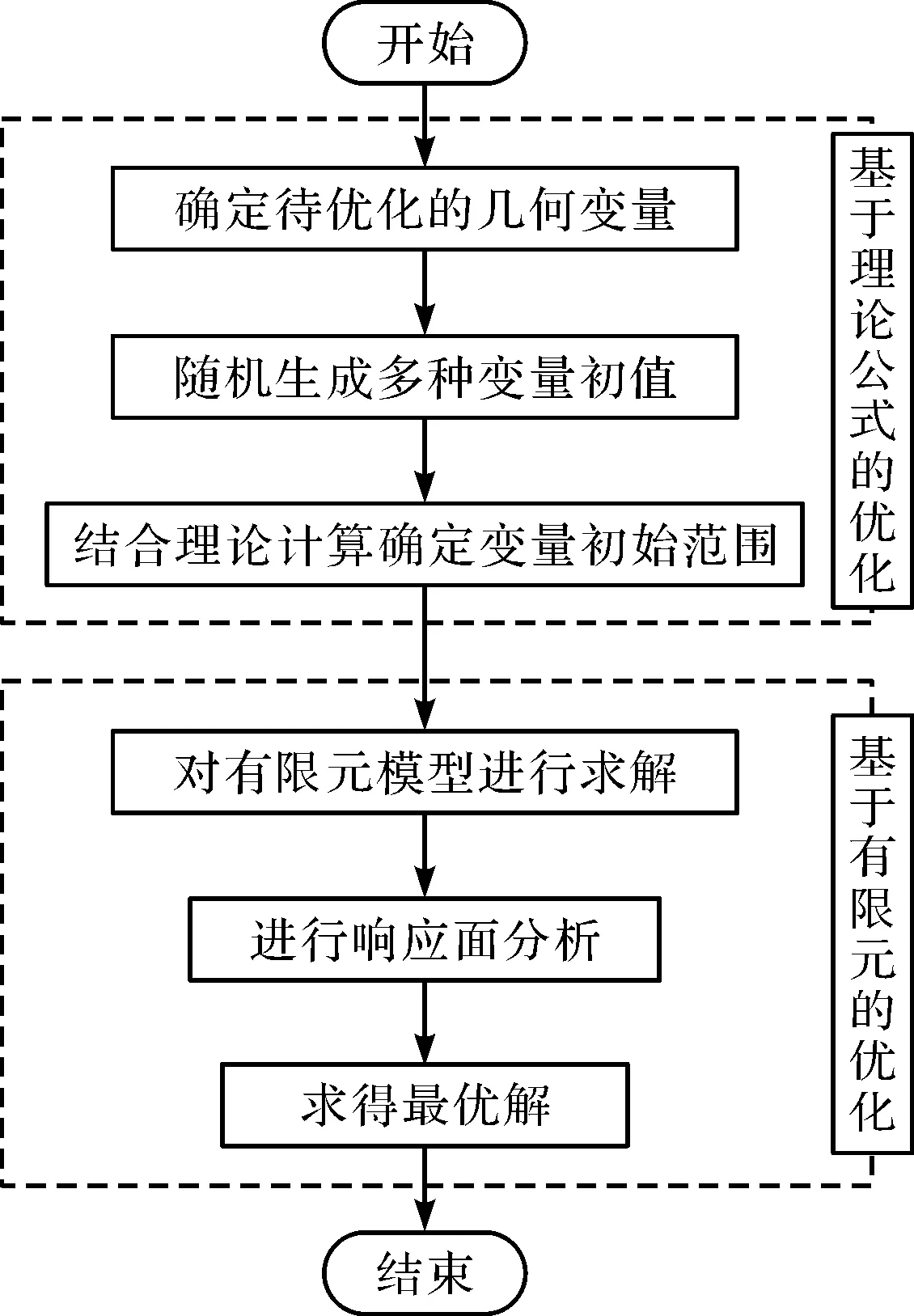
图6 两步式优化策略求解流程图

3.1 基于理论计算的模型补偿

脱皮机转子转速为400 r/min,转子所受离心载荷为:

(1)

式中:ρ—纵梁材料密度,g/mm3;S—纵梁截面面积,mm2;ω—纵梁作回转运动的角速度,rad/s;l—纵梁总长度,mm;r—纵梁上表面距回转中心距离,mm。

当转子工作时,转子发生径向膨胀,其拟合曲线如图5所示。为保证受载后纵梁接近水平,结合镜像补偿理论[13-14]。结合镜像补偿方法,对纵梁上任意节点的补偿量为:

pi=Di

(2)

式中:pi—任意一点的补偿量,mm;Di—任意一点的变形量,mm。

镜像对称补偿方法原理如图7所示。

图7 镜像对称补偿示意图

图7中,未填充的图案为未受载的结构形状,填充的图案为受载条件下的结构形状。

良好的刚性是评估机械结构性能优劣的关键因素。在本文中为进一步提高结构强度,选取安全系数为1.5。当安全系数即许用应力与当量应力值之比小于1.5时,认为此时优化不符合安全标准,优化失败。

脱皮机转子在工况下工况单一、运行平稳,故在本文中只需考虑其在静态下的许用安全系数,安全系数n的计算方法为:

(3)

式中:n—许用安全系数,MPa;σ0—许用应力,MPa;σ—当量应力,MPa。

3.2 基于有限元方法的模型补偿

3.2.1 纵梁扫掠路径的描述函数

常态下转子纵梁截面的扫掠路径为一条长为1 700 mm的直线,为实现结构补偿,需要将扫掠路径离散为大量的散点,以点坐标的变化实现扫掠路径的变化。但当离散点取的过多时,迭代过程中,变量数目过多,计算量过高。本文选取扫掠路径在空间内的重要坐标为特征点,并将特征点进行曲线拟合,作为纵梁截面扫掠路径。

扫掠路径如图8所示。

图8 控制节点示意图

在笛卡尔坐标系内分别取9个坐标点,将9个点拟合为转子纵梁的扫掠路径,扫掠路径有9个变量,分别为p1-p9。

3.2.2 参数灵敏度分析

根据灵敏度分析,笔者对上述参数进行筛选,重新选取参数,上述取法可以减少计算规模,以利于较快获得最优解。参数灵敏度可表述为输入参数对输出参数影响水平的高低,可表征为函数的一阶导,若一个函数可表示为f(p1p2…pn),则关于其输入参数pi灵敏度方程为:

(4)

式中:Se—参数灵敏度水平;f(pi)—输出变量;pi—输入变量。

灵敏度分析结果如图9所示。

图9 参数相关性水平

根据图9分析结果,p1,p3,p8,p9与最大变形量呈负相关,其余参数呈正相关;本文选取灵敏度|S|≥5的变量作为输入变量,即选取p1,p4,p5,p6,p7,p8为最终的输入变量。

3.2.3 转子的变形补偿

对转子的变形补偿问题,可通过优化设计的方法来进行解决。经参数灵敏度筛选,可知最终优化变量为6个,由此便可以得到一个6维的设计域,考虑到状态变量约束,可进一步得到可行域,并在可行域内寻找问题的最优解,其优化设计的数学方程为:

functiontof(x)

(5)

在对转子进行变形补偿分析时,不仅要考虑其变形量对谷物颗粒流通道宽度带来的影响,同时还应考虑纵梁的平直度。关于评估转子的平直度,可在转子纵梁上取等分点,当转子纵梁上变形最大处与变形最小处水平距离越小,则表明转子直线度越高,假设在i处变形量最大,j处变形量最小,则对于评价整条梁的平直度(Str)的计算方程为:

Str=(pi+Dimax)-(pj+Djmin)

(6)

式中:p—纵梁上任一节点的补偿量,mm;D—纵梁上任一节点的变形量,mm。

4 优化实验及结果分析

对于解决多变量优化设计问题,响应面法有着良好的适应性[15,16]。针对脱皮机转子纵梁变形补偿的问题,可采用响应面法加以解决。

参考镜像补偿理论,其优化变量取值范围如表2所示。

表2 参数取值范围

采用中心复合设计方法(CCD)共得到149个样本点,其多元二次线性回归方程如下式:

(7)

式中:n—设计变量个数;f(x)—拟合函数;a0,aii,aji—待定系数;x1～xn—设计变量。

对最大变形量与参数之间的响应进行拟合,其拟合结果计算如下:

(8)

经计算回归模型P<0.01说明模型显著性水平高,R2=0.975 2,表明此次拟合结果较好,上述方程可以用来对转子的变形补偿进行预测和分析。

根据实际生产需求,应在保证脱皮机处理能力的同时,尽可能提升转子的结构性能。可据此建立最大变形量、Str的双重目标优化模型,为保证结构性能,可在优化求解方程中设置Str的权重大于最大变形量的权重。

其目标函数及边界条件为:

(9)

其优化结果如表3所示。

表3 优化实验结果分析表

以未预弯未受载时转子纵梁表面为基准。当转子受载时,记Lu为未补偿状态纵梁上任意一点距基准的位移,Lu的计算方法为:

Lu=Di

(10)

式中:Di—转子上任一节点的变形量,mm。

记La为补偿后纵梁上任意一点距基准的位移,其中预弯后转子距回转中心的距离La计算方法为:

La=|pi-Di|

(11)

式中:pi—转子上任一节点的补偿量,mm;Di—转子上任一节点的变形量,mm。

以表3中所述3个候选点作为算例,其计算结果如表4所示。

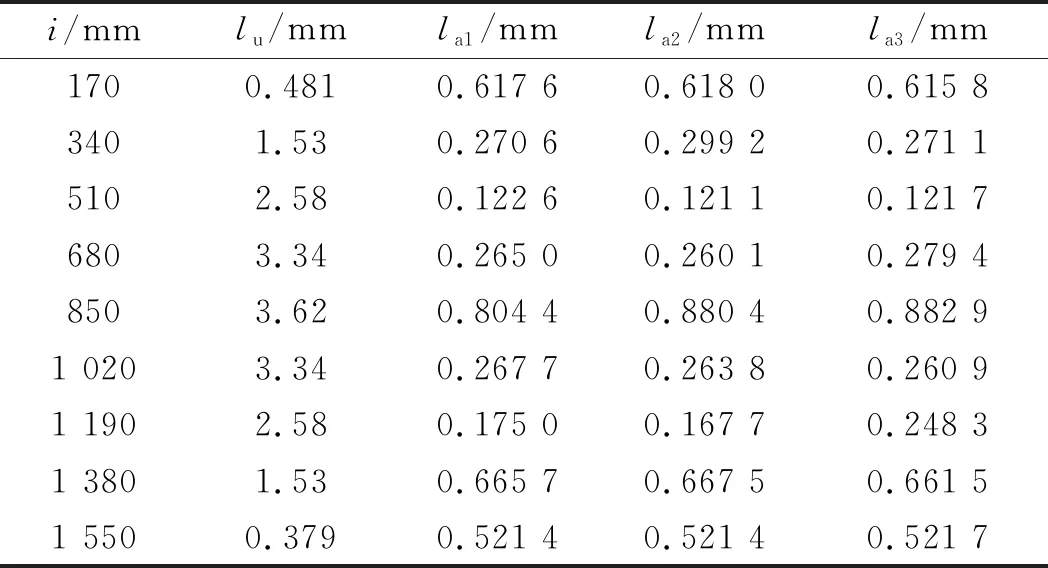
表4 补偿位移效果对比

上述3个候选点的预弯效果如图10所示。

图10 补偿位移结果对比

从图10(a～c)及表4数据中可以得出:镜像对称补偿技术对于抑制脱皮机转子的径向膨胀变形有着显著的效果,对3个候选点进行比较,可知候选点1和候选点2补偿效果最好;同时,结合表中数据可知,候选点2的安全系数最高、应力最小、横梁平直度系数Str最小,故选择候选点2作为此次优化的最优解。

候选点2与初始解在受载条件下的应力、变形、Str值、安全系数对比结果,如表5所示。

表5 优化结果对比

由表4可知:经变形补偿,脱皮机转子结构的最大应力降低了21.5 MPa,为12.89%;其最大变形量降低了0.409 1 mm,为11.31%;Str下降了2.326 5 mm,下降幅度最大为64.30%;安全系数提升了0.208 2,为14.78%。

5 结束语

笔者针对脱皮机转子径向膨胀变形的问题,建立了脱皮机转子的三维参数化有限元模型,并采用两步式优化策略及镜像对称技术,对转子纵梁进行了结构补偿,主要过程及结论如下:

(1)建立了脱皮机转子的有限元模型,并对其在受载条件下的最大应力及最大变形量进行了计算,其最大应力为166.8 MPa,最大变形量3.618 0 mm。为对转子纵梁的变形量进行了曲线拟合,发现其最大变形位置处于沿纵梁长度方向的1/2处;

(2)针对脱皮机转子纵梁径向膨胀变形的问题,采用两步式策略优化方法,对其进行了结构补偿,采用CCD方法得到了147个样本点,对实验结果进行了拟合,经优化得到了3个候选点,对3个候选点数据进行列表以及图像比较,发现取候选点2作为设计参数时,结构最大应力最小,为145.3 MPa;安全系数最高,为1.617 1;评价纵梁平直度的Str值最小,为1.291 5,且此时对颗粒流通道宽度造成的影响最小;

(3)通过变形补偿,脱皮机转子结构的最大应力降低了21.5 MPa,为12.89%;其最大变形量降低了0.409 1 mm,为11.31%;Str下降了2.326 5 mm,下降幅度最大为64.30%;安全系数提升了0.208 2,为14.78%,补偿效果显著。

随着国内农业精细化及农业机械精密化的发展,结构补偿技术将会被逐步广泛地应用于农业装备领域。