管网液压激振系统动态仿真与试验研究*
2021-06-22张慧贤朱德荣郭兆锋杨海军布占伟苗灵霞
张慧贤,朱德荣,郭兆锋,杨海军,布占伟,苗灵霞
(1.洛阳理工学院 机械工程学院,河南 洛阳 471023;2.上海倍伺特自动控制设备有限公司,上海 201818)
0 引 言
由于管网的液压激振属于空间三维振动,将其应用于介质的筛分、脱介等场合,对加快物料的筛分效率,提高透筛率具有重要的理论意义与实际意义。
MODARRES S Y等[1]研究了三维悬臂输送流体的动态特性;寇子明等[2]系统研究了在液压激振作用下,使管网产生可控的多点、多自由度振动的机理及实现方法;陆春月等[3]研究了液压波动激励下的充液管道动态特性,并对应用于制砖机时的振动特性进行了研究;廉红珍等[4]研究了几种液压波动的激振机理,并对其应用于振动筛的振动特性进行了实验研究。
上述工作对充液管道的动态特性及其液压激振的可控性进行了相关性研究,目的在于揭示影响管道振动可控性的因素。若能将管道组成液压管网系统,则这种多点、多自由度的振动可作为激振源,可使机械系统产生三维振动,若将其应用于物料的筛分与脱介,将比传统的二维惯性振动筛具有明显的优势。
使管网产生可控振动的激振源来自于流体,通过产生可控的脉动流体,管网可产生多点、多自由度的三维振动。研究管网在周期性流体激振压力下的动态特性,对于揭示管网激振的运动规律,分析物料在以管网为主参振体上的振动特性非常重要。
针对传统的平面二维振动筛参振质量大、湿分性能较差及工作效率较低的问题,笔者提出一种能够使管网产生可控的多点激振和多自由度振动的液压激振方式[5],并对管网液压激振系统的动态特性进行研究。
1 液压激振系统原理及仿真模型
1.1 系统原理
液压激振系统的原理如图1所示。

图1 液压激振系统原理图
图1中,管网液压激振测试系统由泵、增压缸、电磁换向阀、转阀、管网和传感器等组成,转阀由电动机通过变频器控制,液压油经泵进入增压缸增压后进入转阀,在转阀的作用下一部分进入上管道,一部分进入下管道,在汇流后驱动激振油缸产生周期性的振动[6];随着转阀的旋转,管路中的流体的高低压波不断交替,驱动管网产生振动。
在该试验系统中:
发生激振的管道长为2 m,管道内径为25 mm,壁厚为5 mm;
泵的额定转速为1 500 r/min,额定压力为31.5 MPa,公称排量为63 mL/r;
转阀驱动电机的磁极对数为3,功率为1.5 kW;
变频器功率为3 kW;
系统中安装的压力变送器、位移传感器为两线制标准信号(4 mA~20 mA)。
1.2 仿真模型
笔者利用AMESim软件对该管网液压激振系统进行建模与仿真。
由于AMESim为多学科领域复杂系统建模仿真平台,可通过机械库、液压库、液压元件设计库、液阻库、信号库等,根据实际环境建立接近真实的仿真模式[7-13]。笔者依次通过草图、子模型、参数、仿真4种工作模式,分别进行系统的图形化物理建模。
该液压转向系统建模步骤如下:
(1)在sketch草图模式下建立液压系统原理图,若标准库中不包含所需元件,可以在HCD液压元件设计库中自行建立;
(2)在sub model子模型模式下为系统中的每个元件定义子模型,然后在parameter参数模式下为系统中的元件设置物理参数;
(3)在run模式下运行该系统的仿真模型,并通过plot得出其仿真结果。
根据图1液压激振系统原理图,笔者建立了液压激振系统的仿真模型,如图2所示。

图2 液压激振系统仿真模型
在图2的仿真模型中,笔者考虑到系统的特点,管道模型选择DIRECT,其他元件子模型按默认方式选择。
仿真模型中主要元件参数与实际液压激振系统一致。具体的系统参数如表1所示。
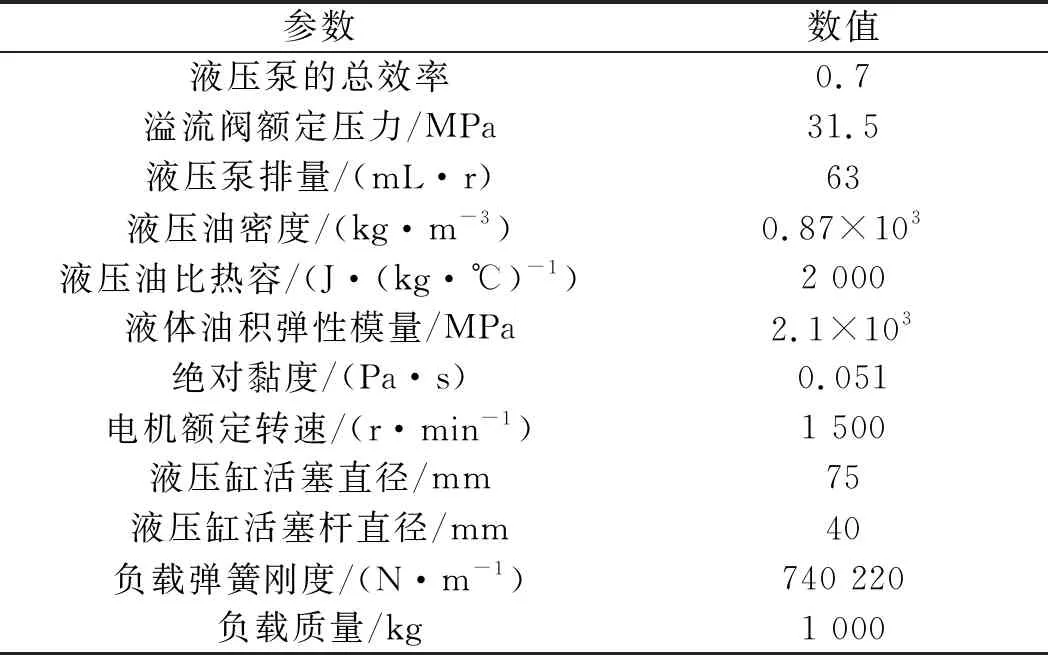
表1 系统参数
2 动态仿真与结果分析
图1中,来自液压泵的流体经三位四通电磁阀1,对液压增压缸进行连续增压,增压后的流体进入液压激振系统。转阀用电磁阀2代替,对图2所示的液压激振系统进行20 s的仿真。
三位四通电磁阀1不得电时处于中位;0 s~1 s为电磁换向阀左位工作;1 s~2 s为电磁换向阀右位工作。三位四通电磁阀2不得电时处于中位;0 s~0.2 s为电磁换向阀左位工作;0.2 s~0.4 s为电磁换向阀右位工作。
在Amesim中,设置电磁换向阀的运行方式为“循环”方式,则流体经过增压后,在节流阀处的压力、流速曲线如图3所示。

图3 增压后流体压力与速度曲线
从图3可以看出:流体经过增压缸增压后,在进入转阀之前为压力与流速脉动的流体,符合液压激振系统对流体的要求。
当流体经过转阀(电磁阀2)后,进入由软管、钢制管网、激振油缸及外部负载构成的液压激振系统,此时流经管网流体的压力与流速如图4所示。

图4 液压激振系统流体压力与速度曲线
对比图3、图4可以看出:流体进入液压激振系统之后,压力与流速均发生了较显著的变化,流体在管路中产生了周期性激振的高低压波,将驱动管网产生振动。
为研究流体参数对管网振动的可控性,下面笔者将研究流体不同工况对激振参数的影响。
2.1 溢流阀设定压力对激振压力的影响
此处的液压泵站采用的是定量泵,并配合节流阀进行流量控制;其负载质量为1 000 kg,液压泵驱动电机工作在额度转速1 500 r/min。
当设定溢流阀压力分别为10 MPa、20 MPa及31.5 MPa时,激振油缸左腔压力曲线如图5所示。
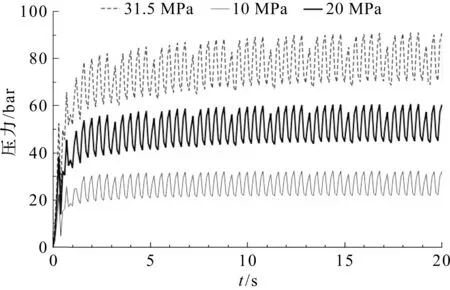
图5 系统压力对激振压力的影响
图5表明:随着系统压力的升高,激振油缸的压力也随之增大,符合定量泵-溢流阀液压系统的控制特点,同时也表明了激振压力的可控性。
2.2 换向频率对激振压力的影响
改变转阀(电磁阀2)的换向时间,当换向时间分别为0.1 s、0.2 s和0.6 s时,激振油缸左腔压力曲线如图6所示。

图6 换向频率对激振压力的影响
图6表明:在一定范围内,随着转阀换向时间的延长,即换向频率的减小,激振压力有上升的趋势。该结果表明了激振压力与换向频率的受控关系。
2.3 溢流阀设定压力对振幅的影响
为研究系统压力对激振油缸活塞杆振幅的影响,笔者保持系统的负载质量为1 000 kg,转阀(电磁阀2)换向时间为0.2 s,液压泵驱动电机转速1 500 r/min。
当设定溢流阀压力分别为10 MPa、20 MPa及31.5 MPa时,激振油缸活塞杆振幅的变化曲线如图7所示。

图7 系统压力对振幅的影响
图7表明:随着系统压力的升高,激振油缸活塞杆振幅逐渐增大。该结果表明,改变系统压力可以对激振油缸活塞杆振幅进行控制,同时也体现了系统压力与振幅之间的控制关系。
2.4 换向频率对振幅的影响
为研究转阀换向频率对激振油缸活塞杆振幅的影响,当负载质量为1 000 kg,液压泵电机转速1 500 r/min,以及溢流阀设定压力为31.5MPa时,改变转阀的换向时间,当换向时间分别为0.1 s、0.2 s和0.6 s时,激振油缸活塞杆振幅变化曲线如图8所示。
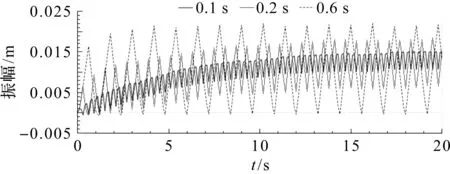
图8 换向频率对振幅的影响
图8表明:随着转阀(电磁阀2)换向频率的增大,激振油缸活塞杆振幅逐渐减小。该结果表明,活塞杆振幅可以通过转阀的换向频率进行控制。
3 试验与结果分析
笔者根据图1所示的系统原理图开发了液压激振试验系统,其中液压系统包括液压泵站、激振油缸、控制阀及连接管道;控制部分由变频器、电机及转阀组成;数据采集单元由PCI采集卡、采集软件及上位计算机组成。
该试验系统如图9所示[14-18]。

图9 液压激振试验系统
笔者采用位移传感器、信号调理器及数据采集卡,对图1液压激振系统激振油缸活塞杆进行振动测试。
试验工况为:负载质量为1 000 kg,液压泵电机转速为1 500 r/min,溢流阀压力分别为10 MPa、20 MPa及31.5 MPa,转阀(电磁阀2)换向时间为0.2 s。
为消除随机干扰信号及高频信号,笔者首先采用最小二乘法消除振动信号的趋势项,然后采用五点滑动平均法对振动信号进行滤波处理。
不同工况下实测的振幅时程曲线如图10所示。
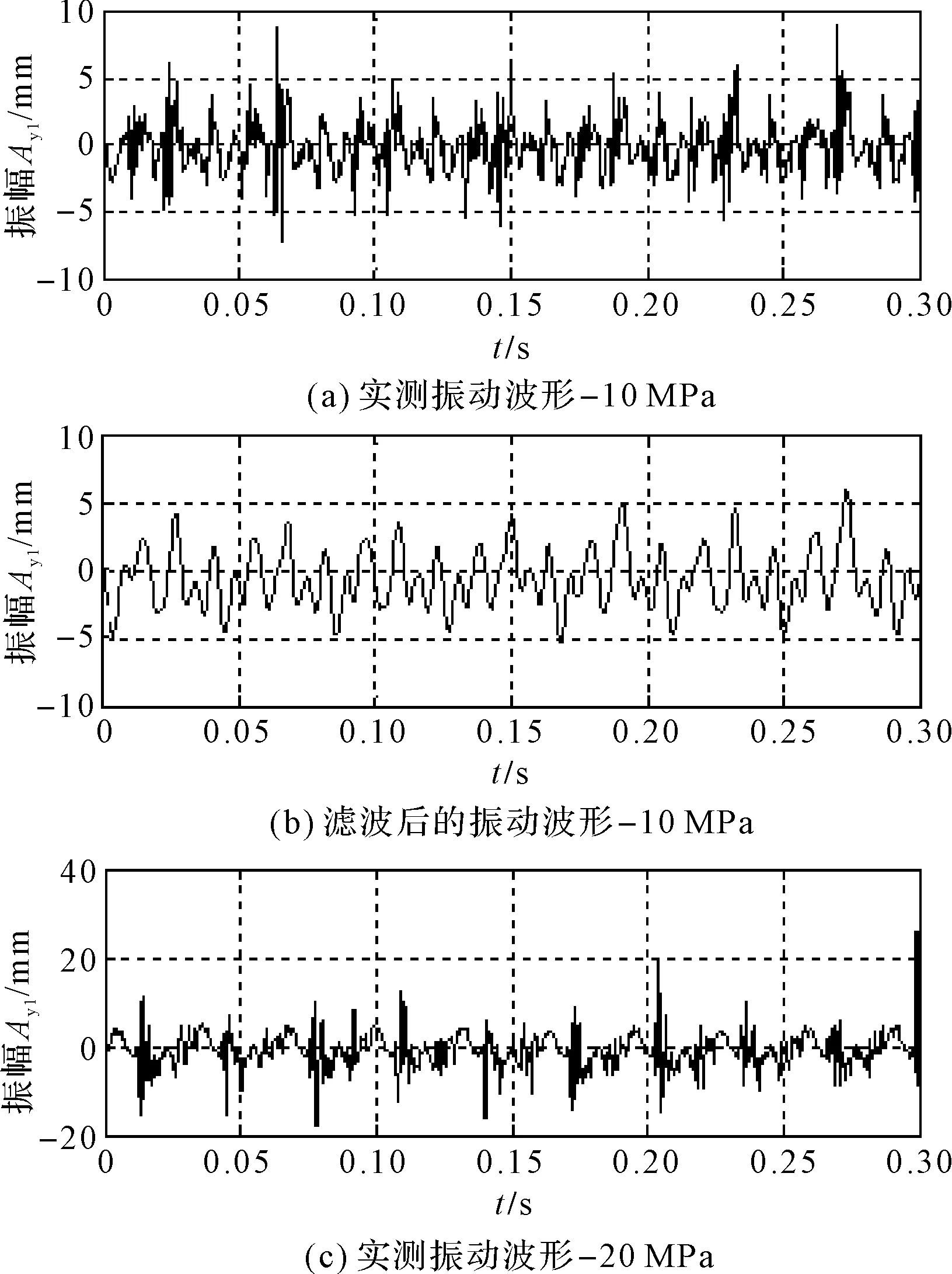
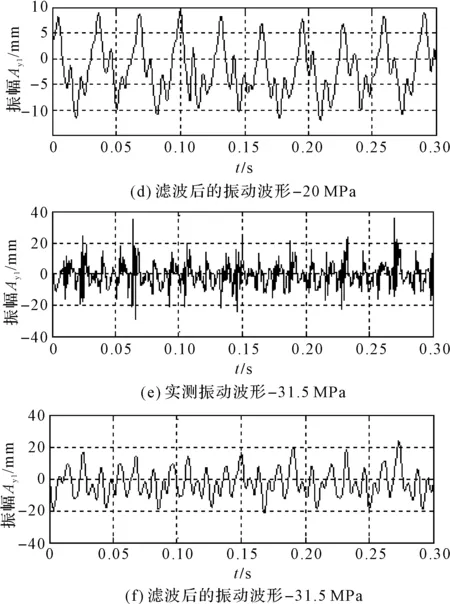
图10 不同工况下实测的振幅时程曲线
图10(a,c,e)为不同系统压力下实测的振动波形,图10(b,d,f)为对应的滤波后的振动波形。图10(b,d,f)表明:五点滑动平均法能较好地消除振动信号的高频干扰,有利于揭示液压激振系统的振动特性。
图10及图7显示了经滤波后的试验实测振动曲线与仿真曲线,经过对比可以发现:其振幅的大小,以及振幅随压力的变化趋势较吻合;且激振油缸的振幅随系统压力的升高而升高。
由于在文献[1]中,已证实该液压激振系统的压力与管网的振幅成线性关系,图1所示的振动管网,其振幅亦随系统压力的升高而升高,表明了该管网激振是可控的。
系统压力分别为10 MPa、20 MPa及31.5 MPa时,转阀换向频率、系统压力与激振油缸振幅之间的关系,如图11所示。

图11 转阀换向频率、系统压力与振幅之间的关系
图11表明:激振油缸振幅随系统压力的升高而升高,随转阀换向频率的升高而减小。由于系统压力可通过溢流阀调节,转阀换向频率可通过变频器调节,可以表明该系统的激振参数是可控的。
以上结果揭示了基于管网液压激振系统振动参数之间的耦合关系,表明了该新型液压激振参数的可控性,以及使管网产生可控的多点激振和多自由度振动的可行性;同时也表明,基于AMESim的管网液压激振系统模型能真实反映系统的动态特性,该结果为液压激振系统的设计与分析提供了一种新途径。
4 结束语
本文提出了一种能够使管网产生可控的多点激振和多自由度振动的新型液压激振方法,开发了基于管网激振的液压激振测试系统,建立了基于AMESim的仿真模型,研究了溢流阀设定压力、转阀换向频率对激振压力及激振油缸活塞杆振幅的影响,对液压激振系统进行了振动测试,对振动信号进行了滤波及平滑处理揭示了液压激振系统转阀换向频率、系统压力与振幅之间的耦合关系。研究结果表明:
(1)激振压力随系统压力的增大而增大,随转阀换向频率的增大而减小;活塞杆振幅随系统压力的升高而升高,随换向频率的增大而减小;
(2)试验测试结果与仿真数据吻合较好,验证了该新型液压激振参数的可控性,以及使管网产生可控的多点激振和多自由度振动的可行性;
(3)基于AMESim的管网液压激振系统模型能真实反映系统的动态特性,为液压激振系统的设计与分析提供了新途径。
