顾及降雨量因子的自适应卡尔曼滤波模型在滑坡变形预测中的应用

李绍建

(宁波市镇海规划勘测设计研究院，浙江 宁波 315200)

0 引 言

滑坡是世界上最主要的地质灾害类型之一。滑坡不但会严重破坏山区的局部环境，还会让山区里的人民的生命财产受到严重的威胁[1]：损坏交通、水利、电力、通信等设施，破坏或污染饮用水源，冲毁良田及经济作物，形成堰塞湖，等等，使人民生活于恐慌之中；更甚者会掩埋城镇、村庄，摧毁风景区、工矿区，造成大量人员伤亡和重大经济损失。

降雨型滑坡，即由降雨引发的滑坡，是常见的滑坡类型之一。诱发滑坡的因素有很多，但常言道“治坡先治水”“无水不滑坡”，可见，由降雨(地下水)引发的滑坡较为突出[2]。降雨增大了滑坡体的孔隙水压力，而且滑坡体的自重量增加，容易造成坡体滑动；降雨浸泡和软化了滑动面，降低了滑坡体的抗剪强度，也容易导致坡体滑动；滑坡体的干湿交替使岩土体开裂，产生节理裂隙，同样容易导致坡体滑动。

滑坡体在内因和外因的作用下逐渐失稳，产生形变。这种形变过程可以理解为滑坡体状态改变的一种信号——随时间和环境因素不断变化而产生的，那么，将卡尔曼滤波模型应用于滑坡体形变进行分析，分别估计出每个监测点的状态参数，由点及面，从而反映出整个滑坡体的运动状态[3]。

1 滑坡变形的卡尔曼滤波模型建立

如前所述，认为滑坡体的变形过程是一个随机过程，同时认为位移速度的均值是不变的。基于此，针对滑坡体变形建立如下方程。

(1)状态方程。滑坡体的变化比较缓慢，可仅将位置和位移速度作为状态参数，而将位移加速度视作随机干扰。

设s(t)是滑坡体某监测点在t时刻的位移，v(t)是速度，a(t)是加速度，则有：

(1)

(2)

(2)观测方程。又设l(t)是滑坡体某监测点在t时刻的观测位移， Δ(t)是观测噪声，则有：

(3)

(3)状态方程、观测方程的离散化。将式(2)和式(3)分别离散化后得到：

(4)

(5)

2 顾及降雨量因子的自适应卡尔曼滤波模型

为了解决传统卡尔曼滤波的滤波发散问题，Sage和Husa提出了自适应卡尔曼滤波模型，该模型原理很简单，应用较广泛。针对降雨型滑坡建立的顾及降雨量因子的自适应卡尔曼滤波模型(为了便于描述，以下简称“顾及降雨量模型”)，即在简化的Sage-Husa自适应卡尔曼滤波模型(以下简称“简化Sage-Husa模型”)的基础上，引入降雨量参数。即：

xk+1=Φk+1,kxk+Ψk+1,kuk+Γk+1,kwk

(6)

zk+1=Hk+1xk+1+vk+1

(7)

式中，xk是n维状态向量，zk+1是m维观测序列，Φk+1,k是n×n维非奇异状态一步转移矩阵，uk为降雨量影响因子，Ψk+1,k为降雨量因子的系数，Γk+1,k是n×p维过程噪声输入矩阵，Hk+1是m×n维观测矩阵，wk和vk+1为相互独立的带时变均值和协方差矩阵的正态白噪声序列。

式中，δkj是Kronecker-δ函数，Qk是wk的方差矩阵，Rk是vk的方差矩阵。

状态一步预测

(8)

一步预测误差

(9)

一步预测误差方差阵

(10)

滤波增益矩阵

(11)

状态估计

(12)

状态估计误差方差阵

Pk+1=[I-Kk+1Hk+1]Pk+1,k

(13)

时变噪声统计估计器

(14)

(15)

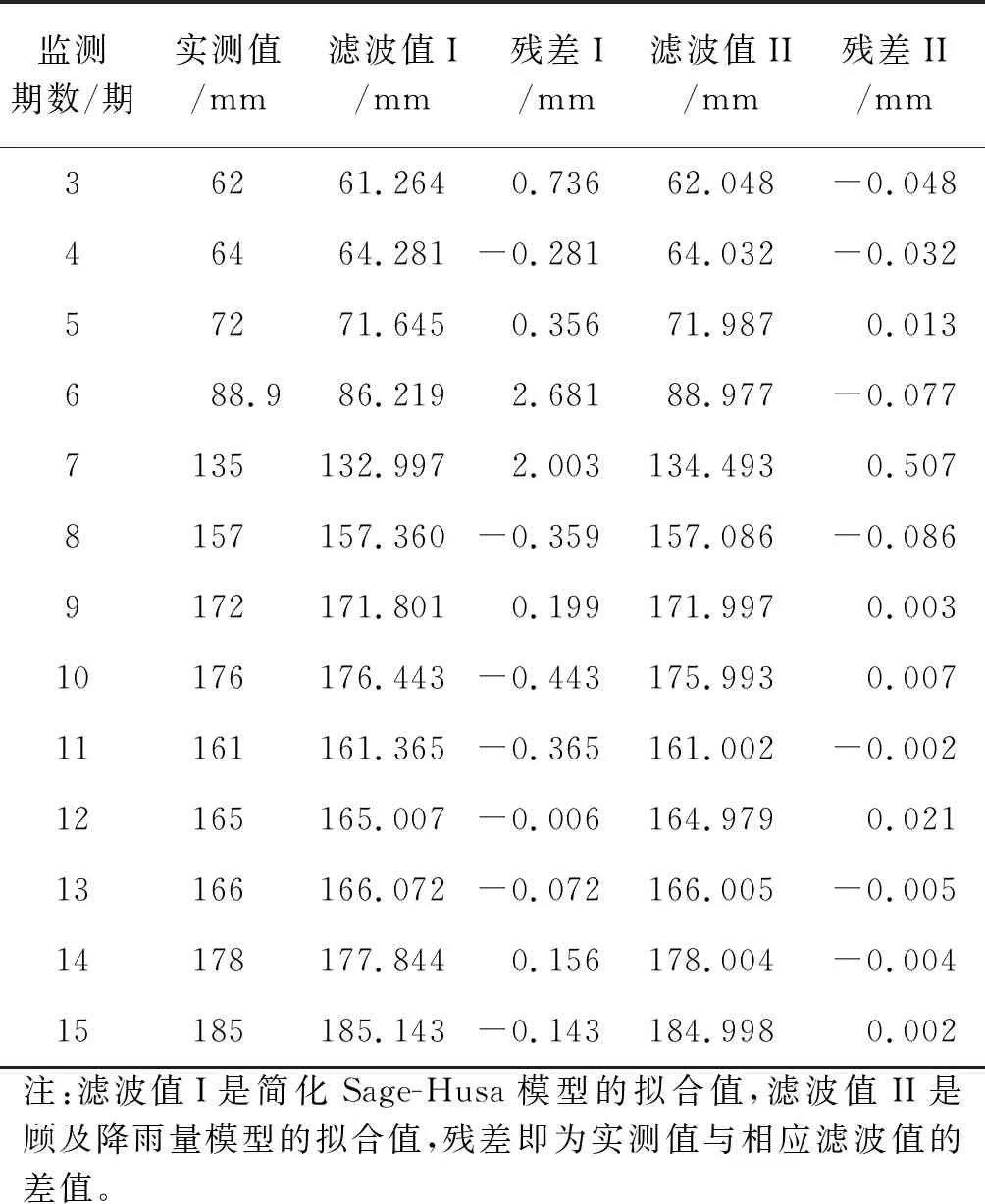
式中，Pk为误差方差矩阵，Kk为滤波增益矩阵，dk=(1-b)/(1-bk+1),0

3 算 例

本文研究的滑坡体处在一个斜坡地带，是古泥石流堆积体，西高东低，高差达100多米，是典型的降雨型滑坡。在滑坡体上布设了多个GPS变形监测点位和雨量采集点位。采用静态GPS观测网采集了4年多的位移数据，采用雨量监测仪采集了2年多的日降雨量。本文选取其中某一监测点的观测数据，分别采用简化Sage-Husa模型和顾及降雨量模型进行对比分析研究。

根据前两期的观测数据确定系统的初始值，同时取遗忘因子b为0.98。而降雨量因子的系数Ψk+1,k，通常情况下选值为0.1～0.5，但各滑坡体的降雨情况都不一样，所以只能通过不同取值逐一去对比分析，从而选取一个最适合值。经过分析，本文选取降雨量因子系数为0.337。

简化Sage-Husa模型和顾及降雨量模型的滤波和预测结果如下。

4 结 语

对表1和表2进行分析，得出以下结论：

表1 两种模型滤波值与实测值对比

表2 两种模型预测值与实测值对比

(1)自适应卡尔曼滤波模型及其改进模型均能很好地反映了该滑坡体变形的实际情况，体现了卡尔曼滤波对动态数据的实时处理能力；同时，本文提出的顾及降雨量因子的自适应卡尔曼滤波模型所得的残差最大为0.507 mm，最小为0.002 mm，其绝对均值为0.062 mm，且都不超过1 mm，滤波效果优于自适应卡尔曼滤波模型，能够更好地拟合该滑坡体的运动状态。

(2)本文提出的顾及降雨量因子的自适应卡尔曼滤波模型的预测效果更好，再次说明了顾及降雨量因子的自适应卡尔曼滤波模型能够较好地反映了该滑坡体的位移和速率变化情况。但是，对于较长期数的预测，从表2残差数据可以看出，两种模型均不适宜。

(3)在分析降雨型滑坡变形的过程中，降雨(地下水位)对滑坡体的影响不容忽视。本文中提出的顾及降雨量因子的自适应卡尔曼滤波模型，无论是滤波精度，还是预测效果，都更加优秀，说明该模型更加真实地反映了该滑坡体的变形情况。