基于后缀法与遗传退火算法的简约树构建
2021-06-21刘清雪
刘清雪, 王 亮
(吉林建筑科技学院 计算机科学与工程学院, 吉林 长春 130111)
0 引 言
系统发生是指生物形成或进化的历史[1]。系统发生分析是在所有可以系统发生过程中寻找最能真实反映历史的发生树,研究物种之间的进化关系。系统发生树的构建是一个NP问题,现在最常用的构建进化树的方法有距离法、最大简约法和最大似然法。最大简约法是基于最优原则的建树方法之一,其前期基础是“多序列比对”,研究结果以树的形式进行描述,并根据有无共同的祖先将其分为有根树和无根树。
1 基础理论与算法分析
系统发生树也称进化树,一般以二叉树的形式表示,它是由一系列代表当前物种的叶子节点和代表推断的祖先或进化事件发生的位置内部节点组成。根据系统发生树能否推断出共同祖先和进化方向分为有根树和无根树。树的分支式样无论有根还是无根均被称为拓扑结构。系统发生树可能的个数随序列个数急剧增加。由N个物种建立系统发生树,则可能的有根树(NR)和无根树(NU)的数目为:
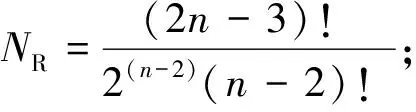
(1)
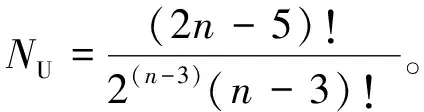
(2)
1.1 后缀法
二叉树的遍历是二叉树最基本的操作,一次完整的遍历可以产生树中所有结点的一个线性序列。设L,V,R分别表示在位于某个结点时移到左子女、访问结点数据和移到右子女的操作,按从左到右的顺序遍历,则存在三种遍历方式,即LVR、VLR、LRV。根据V与L和R的相对位置,分别称这三种为中序、前序和后序遍历。如果用二叉树表示表达式,则对其进行中序、前序和后序遍历产生的线性序列与表达式的中缀、前缀和后缀自然对应。
1.2 简约法
简约法的理论基础是解释一个过程,最好的理论是所需假设数目最少的一个。最大简约法通过分析待比较序列的信息位点,确定相应的系统发生树,该树能用最小的动作产生序列的差异。树的代价计算就是沿着各个分支累加最小核苷酸替换总数。具体实现算法为当内部节点的两个直接后代节点的核苷酸相交为非空时,该节点最可能的候选核苷酸集就是这个交集;否则为它的两个后代节点上核苷酸的并集。当一个并集成为一个节点的核苷酸集时,通向该节点分支的某个位置上必定发生一个核苷酸替换,在统计过程中,只考虑信息位点的替换即可。一般来说,最大简约法适用于以下情况:待检序列的碱基数目大,但差异小;碱基变异率近似相等;没有过多的颠换、转换倾向[2-3]。
1.3 遗传算法[4-5]
遗传算法是模拟生命进化的随机搜索算法,是一种解决复杂优化问题的通用框架。该算法首先按规则产生一定规模的初始群体,然后使其中的个体按一定的概率进行选择、交叉与变异,并按照特定的适应度评价函数进行判断,选择复制优秀个体,组成新的一代,从多个可行解开始,按一定的遗传方式进行迭代,并趋于最优解,但其具有随机漫游性、早熟性等特点,会使局部最优。
1.4 模拟退火算法[6-9]
模拟退火算法模拟固体退火过程,将固体加热至高温时,其内能增大,内部粒子变为无序状,在其慢慢冷却直至常温的过程中,内能逐渐减少,并在基态时达到最小。由初始解i和初始温度t0开始,对当前解重复“产生新解→计算内能模拟函数差(fi-fj)→接受或舍弃”的迭代,并逐步衰减温度t值,算法终止时,当前解即为所得近似最优解,其以一定的概率P接受恶化解的特性将有效规避遗传算法的早熟性。
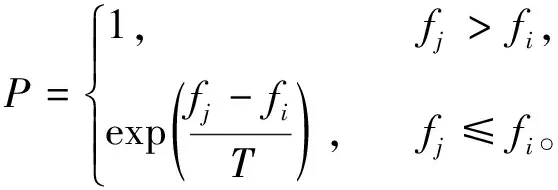
(3)
2 改进算法----基于后缀法编码的遗传退火简约法
2.1 编码方式、适应度函数和种群初始化[10]
2.1.1 编码方式
对于有n个物种的有根二叉树,其中内部结点用“+”表示,叶子结点用数字n表示,连续的2个数字和1个“+”表示一个最小的分枝。
2.1.2 适应度函数
以简约法中整个树的信息位点突变数量为适应度函数,树长为适应值,并以历史最大简约树为最终的最大简约树。
2.1.3 种群初始化
根据输入的n个物种及n-1个内部结点,随机排列产生后缀编码序列。
2.2 遗传退火算子设计
根据后缀法的编码方式及特点,设计了选择退火操作、复制操作、叶子交换退火操作、叶子与分枝交换退火操作、分枝与分枝交换退火操作。
2.2.1 选择退火操作
采用随机遍历抽样法随机选择两个初始个体Pi和Pj,计算其对应二叉树的树长fi和fj,如fi≤fj,则选择个体Pi遗传到下一代;否则,以一定的概率P接受Pj,以此保存物种的多样性。
2.2.2 复制操作
将种群中序列按后序遍历的方法转换成对应的二进制树,再通过适应度函数计算树长,并根据适应度值进行排序。
2.2.3 交换退火操作[11]
对群体中的个体,以一定的概率将指定两位点的序列进行交换。同时要确保经过变异后产生的解依然满足二叉树的定义,不会产生不可行解,因此设计以下三种交换子。
2.2.3.1 叶子交换退火操作
在亲代的后缀编码序列中随机选择两个叶子位置,以2,7为例进行交换,8个叶子二叉树及其后缀编码如图1所示。


图1 8个叶子二叉树及其后缀编码
交换后形成新子代树结构及编码序列如图2所示。
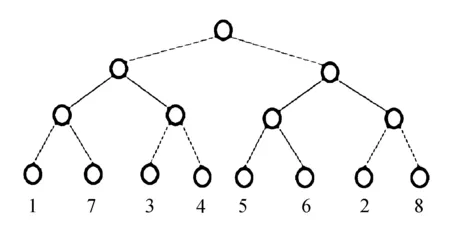

图2 叶子交换后二叉树及其后缀编码
此种交换是单位点的交换,树的拓扑结构没有变化,进化速度较慢,概率值较高。计算交换前后两个体适应度值fi和fj,适应度值低的绝对保留,但也以一定的概率P接受恶化的适应度值高的解。
2.2.3.2 叶子与分枝交换退火操作
在亲代的树型结构中随机选择一个叶子位置和一个分枝位置,以2和(7,8)为例,将其交换。交换产生的子树结构及编码序列如图3所示。

图3 叶子与分枝交换后二叉树
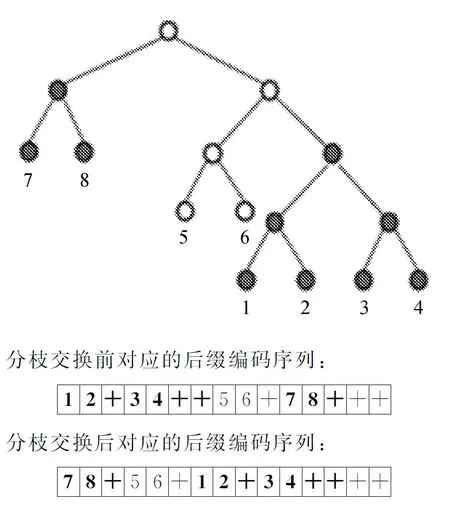
图4 分枝与分枝交换后二叉树
此种交换后树的拓扑结构发生变化,进化速度最快,为了控制结果的鲁棒性,概率值应较低。计算交换前后两个体适应度值fi和fj,选优遗传到下一代的同时,同样以一定的概率P接受恶化解。
2.3 更新初始群体
将新产生的序列和原有序列共同作为下一次迭代的初始群体。并将当前群的最佳个体与历史最佳个体进行比较,以低者作为历史最佳个体。
2.4 结束条件
群体迭代次数达到预定值或进化N代以后,最大简约树的树长不再变化,这时,便可将最后一代进化中最佳个体作为最大简约树。
2.5 算法流程
算法流程如图5所示。
3 模拟实验与结果分析
文中序列资料来源于https://treebase.org/treebase-web/home.html[12]的TreeBASE数据源。以算法的空间、时长和最大简约树的树长为衡量标准,Phylip是一个综合的系统发生分析软件包,其中Dnapars是采用最大简约法对原始数据和重采样数据进行系统发生树构建,文中将改进算法与Dnapars软件相比较。实验环境:CPU,intel(R)Core(TM) i3-2100@3.10 GHz,RAM,8 GB,WIN32位操作系统。鉴于各算子对早熟现象的影响程度分析,经过反复调整,算法参数如下:群体规模为500,最大迭代次数为500次,选择算子为随机选择,叶子交换k1=0.003,叶子与分枝交换k2=0.002,分枝与分枝交换k3=0.001[13-14]。

图5 改进算法流程
用简约法构建系统发生树时,运行时间和树长一直是两个非常重要的指标,且随着物种的增多和序列长度的增加,这两个指标显示尤为重要。树长越小,树越准确,时间越小,算法更优。两种算法实验结果对比见表1。

表1 两种算法实验结果对比表
从表1中数据明显可以得出,改进算法在这两个指标上都有明显提升,且随物种和序列长度的增加,这种提升越明显。因为在编码过程中,后缀法编码采用数组的方式进行存贮,使遗传操作在线性时间内完成,退火算子的引入又保持了物种的多样性,跳出了局部最优解,本算法能在时间和空间两个维度将进化树的构建算法得以改进。
